Метод представления трех work-stealing деков в двухуровневой памяти

Эффективность работы распределенных систем во многом зависит от равномерной загруженности потоков. Ярким примером этого являются параллельные [1, 2] и облачные [3, 4] вычисления, где равномерная нагрузка потоков обеспечивается за счет различных стратегий балансировки задач между ними. Для задач, характеристики которых заранее известны, используют стратегию статической балансировки. Если характеристики задачи не известны или могут меняться (например, система работает в реальном времени), используют стратегию динамической балансировки [5] . Такие стратегии бывают централизованными (распределением задач занят специальный поток) и децентрализованными (каждый поток участвует в распределении задач) [6] .

Work-stealing является распространенным методом децентрализованной динамической стратегии балансировки задач [7, 8] и реализован в широко используемых балансировщиках: Cilk; dotNET TPL; Intel TBB; X10. Принцип метода в том, что поток без задач перехватывает («steal») их у других потоков [9] . Для этого используется специальная структура данных, work-stealing дек, в котором находятся указатели на задачи.

В целом, work-stealing дек является деком («double ended queue» или «deque») с ограниченным входом [10] : в один конец элементы добавляются и удаляются по принципу LIFO (Last In, First Out) или «последним пришел, первым вышел», из другого конца только удаляются по принципу FIFO (First In, First Out) — «первым пришел, первым вышел». Каждый поток имеет свой work-stealing дек. Таким образом, когда создается новая задача, указатель помещается (операция «push») на вершину дека. Когда поток готов выполнить задачу, он берет (операция «pop») указатель на нее из вершины своего дека. Когда поток готов выполнить задачу, но его дек пуст, он перехватывает (операция «steal») указатель из основания другого дека. На рис. 1 представлена схема работы такого дека.

steal

Рис. 1. Принцип работы work-stealing дека

Для эффективного применения стратегии децентрализованной динамической балансировки задач, исследуются как способы реализации метода work-stealing [11, 12] , так и способы организации work-stealing деков [13, 14] : в [15] исследуются различные способы представления деков в памяти; в [16, 17] описывается разработка и проводится анализ динамического балансировщика, построенного на основе этого метода.

В этой работе рассматривается следующий способ расположения дека в памяти:

\bullet В быстрой памяти (первый уровень) находятся вершина и основание;

\bullet В медленной памяти (второй уровень) находится середина.

Таким образом, система может быстро обращаться к концам дека, где элементы активно добавляются и удаляются. Для этого способа представления дека возникают задачи разделения и перераспределения памяти.

Модель работы такого work-stealing дека была предложена в [18, 19] . В статьях была решена задача перераспределения двухуровневой памяти для критерия оптимальности: минимизация средних затрат на перераспределение. Модели работы и методы управления двумя work-stealing деками в двухуровневой памяти были рассмотрены в [20] . Модель работы трех work-stealing деков в двухуровневой памяти была предложена в [21] . В предыдущей статье была решена задача разделения памяти для метода представления, где концы деков растут на встречу друг другу в общем участке памяти. В этой статье предлагается модель и исследуется задача разделения двухуровневой памяти для альтернативного метода представления трех work-stealing деков, где концы деков находятся в отдельных участках памяти.

Статья организована следующим образом. В разделе 1 дается описание нового метода и ставятся задачи разделения памяти между тремя деками. В разделе 2 рассматривается имитационная модель процесса и приводится пример ее работы. Результаты исследований, проведенных на основе модели, представлены в разделе 3. В заключении предложены некоторые варианты использования метода и направление дальнейших исследований.

• 1.    Постановка задачи

Пусть в памяти компьютерной системы расположены три work-stealing дека De 1 , De 2 и De 3 . Память системы разбита на два уровня имеющие разную скорость: память первого уровня быстрая, второго — медленная. Чтобы расположить дек в двухуровневой памяти, он разделен на три части (рис. 2) :

• 1.    конец Sk _n , куда указатели на задачи добавляются и удаляются;

• 2.    середина Md _n , где указатели хранятся;

• 3.    конец Qe _n , из которого указатели только удаляются (перехватываются методом workstealing).

  Skn

  
  

  Md Qe nn

  
  

Рис. 2. Разбиение work-stealing дека De _n

Середины трех деков ( Md 1 , Md 2 , Md 3 ) находятся в памяти второго уровня. В памяти первого уровня находятся концы этих деков: активные ( Sk 1 , Sk 2 , Sk 3 ) и концы из которых происходит перехват ( Qe 1 , Qe 2 , Qe 3 ), объединенные в одну очередь Qe . Таким образом, двухуровневая память компьютерной системы, в которой расположены три work-stealing дека, имеет следующий вид (рис. 3) :

\bullet m — общий размер быстрой памяти первого уровня;

\bullet s — участок памяти первого уровня, где находятся объединенная очередь Qe и активный конец первого дека Sk 1 , представленный в виде стека;

\bullet d и m - s - d — участки памяти, в которых расположены активные концы Sk 2 и Sk 3 соответственно.

Характеристики памяти второго уровня и находящихся в ней частей деков Md 1 , Md 2 и Md 3 в этой статье не рассматриваются.

уровень 1

s

d

m-s-d

Qe 1 Qe 2 Qe 3

Sk 1 Sk 2

Sk 3

m

Md 1

Md 2

Md 3

уровень 2

Рис. 3. Расположение деков в двухуровневой памяти

Пусть один указатель на задачу занимает одну единицу памяти. Весь размер быстрой памяти составляет m указателей, размеры концов каждого дека равны между собой Sk i = Qe i = Sk 2 = Qe 2 = Sk 3 = Qe 3 . Система работает в дискретном времени, где на каждом шаге происходят операции влияющие на размер деков. Вероятности этих операций для каждого из деков указаны в табл. 1 ( p n + q n + w n + pw n + qw n + r n = 1).

Таблица 1. Вероятности операций с деком De _n

Обозначение	Описание вероятности
p n	Добавление одного указателя в рабочий конец S k n дека De n
q n	Удаление одного указателя из рабочего конца S k n дека De n
w n	Перехват одного указателя из общей work-stealing очереди Qe , в то время как дек De n обрабатывает задачу
pw n	Параллельное добавление указателя в Sk n и перехват указателя из Qe
qw n	Параллельное удаление указателя из Sk n и перехват указателя из Qe
r n	Операция не изменяющая размеры концов дека De n (обработка задачи)

Время работы системы заранее не ограничено, но она прекращает работу если возникает одно из условий перераспределения памяти: дек De _n пытается забрать указатель из уже пустого конца Sk n (Sk n <  0); общая очередь work-stealing концов деков опустошена Qe <  0; один из участков памяти первого уровня переполнен Qe + Sk i > s, Sk 2 > d или Sk 3 > m — s — d.

Для вышеописанной системы рассматриваются следующие задачи:

• 1.    нахождение оптимального разделения s памяти первого уровня m , если участкам d и m — s — d выделена половина оставшейся памяти ( d = m — s — d = ( m — s ) / 2);

• 2.    нахождение оптимальных значений s и d разделения памяти между тремя деками. Критерий оптимальности: максимальное среднее время работы системы (среднее количество операций) до перераспределения памяти.

• 2.    Имитационная модель

Поставленные задачи были решены с помощью имитационного моделирования. Для корректной работы этой модели, основанной на методе Монте-Карло, некоторые из характеристик системы должны быть заранее известны. Так, значения вероятностей операций с деками должны быть получены в ходе предварительных статистических исследований. Размер общей памяти m фиксирован, в то время как значение разделения s всей памяти m и значение разделения d участка памяти m — s вычисляются в ходе работы модели. На каждом шаге дискретного времени для каждого дека генерируется случайное значение от нуля до единицы, соответствующее одной из вероятности операций с ним. Среднее количество шагов, которые модель проделывает до перераспределения памяти, является средним временем работы t такой системы. Комбинации s и d при которых t принимает наибольшее значение, считаются оптимальными значениями разделения памяти первого уровня m .

Для примера, рассмотрим систему с характеристиками m = 100, s = 50, d = 25, m — s — d = 25 и значениями вероятностей p n = q n = w n = pw n = qw n = 0 . 16 и r n = 0 . 20 (рис. 4) .

pn     qn     wn    pwn    qwn     rn

0     0,16   0,32    0,48    0,64   0,80     1

Рис. 4. Пример разбиения отрезка от нуля до одного между вероятностями операций с деками

Допустим, на шаге моделирования n эта система имеет следующий вид:

• •    Qe = 1;

• •    Sk i = 10;

• •    Sk 2 = 0;

• •    Sk 3 = 25.

Затем генерируется случайные значения, на основе которых совершаются операции с деками. Например: для дека De 1 было получено число 0.24, соответствующие вероятности q 1 удаления элемента из Sk 1 ; для дека De 2 число 0.08, что соответствует вероятности p 2 добавления элемента в Sk 2 ; и для дека De 3 число 0.72 и вероятность qw 3 — операция одновременного удаления элемента из Sk 3 и перехвата элемента из Qe .

Таким образом, на шаге n +1 рабочие концы деков принимают следующие размеры:

• •    Qe = 1 — 1 = 0;

• •    Sk i = 10 — 1 = 9;

• •    Sk 2 = 0 + 1 = 1;

• •    Sk ₃ = 25 — 1 = 24.

Так как переполнение памяти ( Qe + Sk i ^ 50, Sk 2 ^ 25, Sk 3 ^ 25) или опустошение концов деков ( Qe К 0, Sk i К 0, Sk 2 К 0, Sk 3 К 0) не произошло, то система продолжает свою работу. Полученные размеры рабочих концов становятся стартовыми размерами для следующего шага моделирования.

Рассмотрим ситуации, при которых такая система прекратила бы свою работу на шаге моделирования n :

• 1.    Для дека De 2 сгенерировано случайное значение, соответствующее вероятности q 2 , что приводит к опустошению рабочего конца дека ( Sk 2 = 0 — 1 = — 1, Sk 2 <  0);

• 2.    Для дека De 3 получено число, соответствующие вероятности p 3 — память, отведенная рабочему концу дека, переполняется ( Sk 3 = 25 + 1 = 26, Sk 3 >  25);

• 3.    Произошло две подряд операции перехвата элемента ( w _n , pw _n и/или qw _n ) из общей очереди work-stealing концов деков, что приводит к ее опустошению ( Qe = 1 — 1 — 1 = — 1, Qe <  0).

• 3.    Численный анализ

В этой статье моделируется система, где размер общей памяти первого уровня равен m = 100 единиц и начальные размеры концов деков составляют Sk i = Qe i = Sk 2 = Qe 2 = Sk 3 = Qe 3 = 10 единиц памяти. Таким образом, участки памяти могут иметь следующие размеры: участок, в котором расположены конец Sk 1 и очередь work-stealing концов Qe — s = 40 ... 80 единиц; участок, в котором расположен конец Sk 2 — d =10 ... 50 единиц и, соответственно, участок для конца Sk 3 , m — s — d = 10 ... 50 единиц.

В результате работы имитационной модели были получены оптимальные значения разделения памяти ( s , d ) и среднее время работы системы ( t ) для различный вероятностей операций с деками. Вероятности имеют теоретические значения для более легкого сравнения результатов.

В следующих таблицах приведены результаты для задачи нахождения оптимального разделения s памяти m, где участки памяти d и m - s - d имеют одинаковый размер (d = m — s — d = (m — s)/2). В табл. 2 рассматривается система, где указатели чаще добавляются в первый дек (p1 > p2, p1 > p3); в табл. 3 — чаще во второй (p2 > p1, p2 > p3). Система, в которой указатели с большей вероятностью добавляются в два дека (p1 > p3, p2 > p3 и p2 > p1 , p3 > p1 ), анализируется в табл. 4 и 5. Система, где указатели добавляются равномерно в три дека (p1 = p2 = p3) рассматривается в табл. 6.

Таблица 2. Среднее время работы системы при d = ( m — s ) / 2, p 1 > p ₂ и p 1 > p ₃

Вероятности операций	Метод разделения памяти
	Разделение пополам ( s = 50, d =25)	Оптимальное разделение ( s = 66, d = 17)
p 1 = 0 . 50, p 2 = p 3 = 0 . 26, q 1 = 0 . 02, q 2 = q 3 = 0 . 26, w 1 = w 2 = w 3 = 0 . 01, pw 1 = pw 2 = pw 3 = 0 . 01, qw 1 = qw 2 = qw 3 = 0 . 01, r 1 = r 2 = r 3 = 0 . 45	27 . 82	56 . 59
p 1 = 0 . 60, p 2 = p 3 = 0 . 31	22 . 23	46 . 11
p 1 = 0 . 70, p 2 = p 3 = 0 . 36	18 . 50	38 . 91
p 1 = 0 . 80, p 2 = p 3 = 0 . 41	15 . 83	33 . 66
p 1 = 0 . 90, p 2 = p 3 = 0 . 46	13 . 83	29 . 69

Таблица 3. Среднее время работы системы при d = ( m — s ) / 2, p 2 > p i и p 2 > р з

Вероятности операций	Метод разделения памяти
	Разделение пополам ( s = 50, d =25)	Оптимальное разделение ( s = 46, d = 27)
p 2 = 0 . 50, p 1 = p 3 = 0 . 26, q 2 = 0 . 02, q 1 = q 3 = 0 . 26, r 1 = r 2 = r 3 = 0 . 45	32 . 78	36 . 73
p 2 = 0 . 60, p 1 = p 3 = 0 . 31	27 . 18	30 . 31
p 2 = 0 . 70, p 1 = p 3 = 0 . 36	23 . 23	25 . 85
p 2 = 0 . 80, p 1 = p 3 = 0 . 41	20 . 31	22 . 54
p 2 = 0 . 90, p 1 = p 3 = 0 . 46	18 . 05	19 . 98

В целом, оптимальные значения разделения памяти s для каждого набора вероятностей совпадают. Для примера, опишем первый результат из табл. 2. Вероятность добавления указателя в активный конец Sk 1 дека De 1 составляет p 1 = 0 . 50 . Вероятность того, что указатель будет добавлен в конец ( Sk 2 , Sk 3 ) другого дека ( De 2 , De 3 ) равна p 2 = p 3 = 0 . 26 . Если память первого уровня ( m = 100 ) разделена пополам, то участкам памяти выделены следующие размеры: участок, в котором расположены Sk 1 и Qe , s = 50 единиц; участок, в котором расположен Sk 2 , d = 25 единиц; участок, в котором расположен Sk 3 , m — s — d = 25 единиц. Если память разделена оптимально, то размеры участков равны s = 66, d = 17 и m — s — d = 17. Среднее время работы системы до перераспределения памяти первого уровня, где память разделена пополам — t = 27 . 82 операций; системы, где память разделена оптимально — t = 56 . 59 операций. Таким образом, система с оптимально разделенной памятью совершает на 28 . 77 операций больше, чем система у которой память разделена пополам.

Таблица 4. Среднее время работы системы при d = ( m - s ) / 2, P 1 > Р з и p 2 > р з

Вероятности операций	Метод разделения памяти
	Разделение пополам ( s = 50 , d =25 )	Оптимальное разделение ( s = 54 , d =23 )
p 1 = p 2 = 0 . 50 , p 3 = 0 . 26 , q 1 = q 2 = 0 . 02 , q 3 = 0 . 26 , r 1 = r 2 = r 3 = 0 . 45	25 . 78	27 . 89
p 1 = p 2 = 0 . 60 , p 3 = 0 . 31	21 . 08	23 . 17
p 1 = p 2 = 0 . 70 , p 3 = 0 . 36	17 . 84	19 . 89
p 1 = p 2 = 0 . 80 , p 3 = 0 . 41	15 . 48	17 . 48
p 1 = p 2 = 0 . 90 , p 3 = 0 . 46	13 . 66	15 . 66

Таблица 5. Среднее время работы системы при d = ( m — s ) / 2, p ₂ > p 1 и p ₃ >  p 1

Вероятности операций	Метод разделения памяти
	Разделение пополам ( s = 50 , d =25 )	Оптимальное разделение ( s = 45 , d = 27 )
p 2 = p 3 = 0 . 50 , p 1 = 0 . 26 , q 2 = q 3 = 0 . 02 , q 1 = 0 . 26 , r 1 = r 2 = r 3 = 0 . 45	29 . 44	33 . 43
p 2 = p 3 = 0 . 60 , p 1 = 0 . 31	24 . 68	27 . 91
p 2 = p 3 = 0 . 70 , p 1 = 0 . 36	21 . 34	24 . 04
p 2 = p 3 = 0 . 80 , p 1 = 0 . 41	18 . 90	21 . 19
p 2 = p 3 = 0 . 90 , p 1 = 0 . 46	17 . 07	19 . 04

Таблица 6. Среднее время работы системы при d = (m — s)/2, pi = p2 = рз

Вероятности операций	Метод разделения памяти
	Разделение пополам ( s = 50 , d = 25 )	Оптимальное разделение ( s = 52 , d = 24 )
p 1 = p 2 = p 3 = 0 . 50 , q 1 = q 2 = q 3 = 0 . 02 , r 1 = r 2 = r 3 = 0 . 45	24 . 87	25 . 97
p 1 = p 2 = p 3 = 0 . 60	20 . 55	21 . 74
p 1 = p 2 = p 3 = 0 . 70	17 . 54	18 . 81
p 1 = p 2 = p 3 = 0 . 80	15 . 32	16 . 69
p 1 = p 2 = p 3 = 0 . 90	13 . 60	15 . 12

В табл. 7 и 8 приведены результаты для задачи нахождения оптимальных значений разделения памяти s и d. В этих таблицах рассматриваются только системы с большой вероятность добавления указателя во второй дек (p2 > p1 , p2 > p3 и p1 > p3, p2 > p3): оптимальное разделение s, разделение d и время работы t для других наборов вероятностей совпадает с результатами в предыдущих таблицах. Это можно объяснить тем, что значение разделения памяти d зависит от вероятностных характеристик дека De2 и не имеет влияния, если вероятность добавления указателя во второй дек маленькая.

Таблица 7. Среднее время работы системы при d = max , p 2 > p 1 и p 2 > p 3

Вероятности операций	Размер участка памяти m — s ( s = 46)
	Половина участка ( d = 27)	Оптимальный размер ( d = 37)
p 2 = 0 . 50, p 1 = p 3 = 0 . 26, q 2 = 0 . 02, q 1 = q 3 = 0 . 26, w 1 = w 2 = w 3 = 0 . 01, pw 1 = pw 2 = pw 3 = 0 . 01, qw 1 = qw 2 = qw 3 = 0 . 01, r 1 = r 2 = r 3 = 0 . 45	36 . 73	51 . 92
p 2 = 0 . 60, p 1 = p 3 = 0 . 31	30 . 31	43 . 02
p 2 = 0 . 70, p 1 = p 3 = 0 . 36	25 . 85	36 . 72
p 2 = 0 . 80, p 1 = p 3 = 0 . 41	22 . 54	32 . 03
p 2 = 0 . 90, p 1 = p 3 = 0 . 46	19 . 98	28 . 42

Таблица 8. Среднее время работы системы при d = max , p 1 > p 3 и p 2 > p 3

Вероятности операций	Размер участка памяти m — s ( s = 54)
	Половина участка ( d = 23)	Оптимальный размер ( d = 29)
p 1 = p 2 = 0 . 50, p 3 = 0 . 26, q 1 = q 2 = 0 . 02, q 3 = 0 . 26, r 1 = r 2 = r 3 = 0 . 45	27 . 89	34 . 03
p 1 = p 2 = 0 . 60, p 3 = 0 . 31	23 . 17	27 . 95
p 1 = p 2 = 0 . 70, p 3 = 0 . 36	19 . 89	23 . 74
p 1 = p 2 = 0 . 80, p 3 = 0 . 41	17 . 48	20 . 67
p 1 = p 2 = 0 . 90, p 3 = 0 . 46	15 . 66	18 . 31

Аналогично с предыдущей задачей, система с оптимально разделенной памятью работает дольше. Например, проанализируем первый результат из табл. 7. Если участок памяти первого уровня m — s = 54 разделен пополам (d = m — s — d = 27), то система совершает в среднем t = 36 . 73 операций до перераспределения памяти. Если память разделена оптимально: участку, в котором расположены Sk 1 и Qe выделяется s = 46 единиц; участку, в котором расположен S k 2 — d = 37 единиц; участку, в котором находится Sk 3 выделяется m — s — d = 17 единиц. Среднее время работы такой системы составляет t = 51 . 92 операций, т.е. она работает в среднем на 15 . 19 операций дольше. Зависимость среднего времени работы этой системы t от разделения d участка памяти m — s представлена в виде графика на рис. 5.

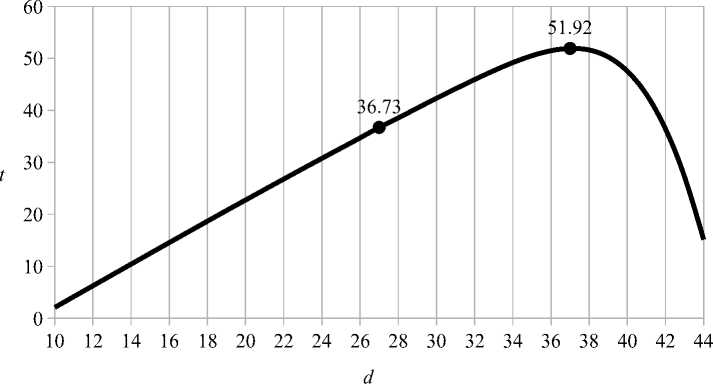
Рис. 5. Зависимость времени работы t от разделения памяти d

Заключение

В статье описывается один из методов представления трех work-stealing деков в двухуровневой памяти, где концы деков расположены в отдельных участках памяти. На основе этого метода была построена имитационная модель и решены задачи оптимального разделения памяти первого уровня между тремя деками для различных теоретических компьютерных систем. В качестве критерия оптимальности используется максимальное среднее время работы системы до перераспределения памяти.

Системы, где участки памяти разделены оптимально, работают дольше систем, память которых разделена поровну. Так, в зависимости от вероятностных характеристик, среднее время работы может увеличится на треть или в два раза.

Задача разделения памяти между деками может возникнуть во время разработки системного программного обеспечения. В таком случае, на основе предложенной модели и предварительного статистического исследования системы, можно найти оптимальные значения разделения быстрой памяти первого уровня.

В будущем можно провести новые исследования не только для других наборов входных данных, но и для других критериев оптимальности, например, минимизация затрат на перераспределение памяти. Также стоит заметить, что в этом методе концы деков расположены в отдельных участках памяти — возможно увеличить число структур данных не изменяя количества участков: концы новых деков следует располагать в участках памяти вместе с уже существующими, пустив их на встречу друг другу.