Метод приближенного аналитического расчета коэффициентов отражения электромагнитной волны от слоя неоднородного невзаимного кирального метаматериала с учетом дисперсии материальных параметров

[g^H © Панин Д.Н. и др., 2025

тельных вычислительных ресурсов и времени [6– 8]. Это создает необходимость в разработке более эффективных методов анализа, которые смогли бы обеспечить быстрое получение результатов без потери точности. В данной работе предложен приближенный метод расчета коэффициентов отражения электромагнитной волны от слоя неоднородного невзаимного кирального метаматериала с учетом дисперсии материальных параметров. Цель исследования состоит в разработке аналитического подхода к решению данной задачи. Считается, что аналитические решения не только ускоряют процесс получения результатов, но также способствуют лучшему пониманию физики процессов взаимодействия волн с неоднородными структурами. Аналитические методы имеют ряд преимуществ: они позволяют быстро оценить влияние различных параметров на коэффициенты отражения и преломления; их можно использовать для предварительного анализа перед проведением более сложных численных расчетов; кроме того, они могут служить основой для дальнейших теоретических исследований и экспериментов.

• 1 . Математическая модель неоднородной и невзаимной киральной среды

Для электрофизических параметров невзаимной неоднородной киральной среды можно записать материальные уравнения в виде [9; 10]:

D = £ 0 ( £ ( x , го ) E + n ( x , го ) Z 0 H ) , B = ц ₀ ( ц ( x , го ) H + n ( x , го ) Z -¹ E ) .

где Z o = ^Ц о До - характеристическое сопротивление вакуума;

п ( X , го ) = х + i в ( x , го ) = п ;

П ( X , ® ) = х- i в ( X , го ) = п ;

X и р ( x , го ) - параметры невзаимности и кираль-ности соответственно; £ ( x , го ) = £ и ц ( x , го ) = ц - относительные диэлектрическая и магнитная проницаемости; го - круговая частота; i = V-1.

При записи соотношений (1) предполагается, что неоднородность материальных параметров кирального метаматериала реализуется только вдоль одной пространственной координаты x .

Материальные параметры неоднородной ки-ральной среды зависят от частоты го , координаты x и имеют следующий вид:

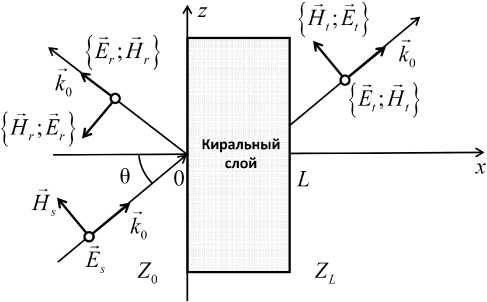
Рис. Геометрия задачи

Fig. Geometry of the problem

£ ( x , го ) = £ _с +

ц ( ^{x , го} ) = Ц с ⁺

^£горез (x) ; горез (x)-го + iVго

• 2             2           ^;

^го рез ( ^x ) ^{-го +} i V ^го

^ % ^го рез ^{( x )го}

х( x, го) = ^“л—Г~ горез (x)-го + i4го где горез( x) - резонансная частота, которая имеет разные значения в произвольной точке пространственной координаты x; у - частота демпфирования; Q„, Q,., Q - коэффициенты, определяющие £ Ц z отклонение значений электрофизических параметров в области резонанса; £с, цс - относительные диэлектрическая и магнитная проницаемости среды-контейнера соответственно.

При записи соотношений (2) учтено, что дисперсия диэлектрической и магнитной проницаемости подчиняются модели Лоренца, а параметр киральности – модели Кондона.

С помощью материальных уравнений в форме (1) и уравнений Максвелла в дифференциальной форме будем решать задачу об отражении плоской однородной электромагнитной волны от неодно- родного невзаимного кирального слоя с учетом дисперсии. Волна падает на границы раздела под углом 0 (рис.). На рис. введены следующие обозначения: {Es; Hs} - векторы напряженностей электрического и магнитного полей падающей волны; {Er; Hr} - векторы отраженной волны и {Et; Ht} - векторы прошедшей волны.

Для слоя из неоднородной невзаимной кираль- ной среды толщиной L, используя материальные уравнения (1) для пространственных зависимостей y- и z-составляющих векторов напряженностей электрического и магнитного полей при гармонической зависимости от времени, получим

систему обыкновенных нений вида		дифференциальных урав-
dEy dx	= - i ГОЦ 0 Ц Hz ( x ) - i ro^	1 ц 0 е 0 n Ez ( x ) ,                (3)
dHz dx	L    sin 2 0 = - i roS 0 S i 1-- | це-nn		■Ey ( x )+
+ i го,	* 2 1 n sin 0 ]Ц 0 е 0 in            * ' | це-nn	H y ( x ) ,
dEz dx	1, sin 2 0 = i юц 0 ц1 1          * | це-nn	J	H y ( x ) -
- i шщ	1 ------1 * n sin 0 Уц 0 е 0 in             * | це-nn	’Ey ( x ) ,

0 E z ( x ) + iщ^^ n * H z ( ^x ) •

—2 = A 7 ( У , K ) U 2 ( У ) + A 8 ( У , K ) V 1 ( У ) , ^{d у}

где

A 1 ( У , K ) = - iK ц ( у , K ) ; A 2 ( У , K ) = - iK n ( y , K ) ;

A 3 ( У , ^K ) =

- iK е ( у , K W1 -

A 4 ( У , ^K ) =

= iK ЫУ , K )

A 5 ( У , ^K ) =

dHy

—— = i шее dx

sin ² 0

ц ( У , K ) е ( у , K ) -n ( y , K ) n* ( У , K )

n ( У , K ) sin ² 0 ц ( У , K ) е ( у , K ) -п ( У , K ) n * ( У , K )

iK ц (у, K )h--------

I ц ( у , K ) е ( у , K ) -n ( y , K ) n ( У , K )

Если ввести в рассмотрение нормированные напряженности электрического U i (x ) = E y ( x )/ E o , U 2 ( x ) = E z ( x у E o и магнитного V 1 ( x ) = Z o H z ( x )/ E o , V 2 ( x) = Z 0 H y ( x )/ E 0 полей, нормированную координату у = x^ и нормированное волновое число K = й^о Ц о L, то уравнения (3) можно записать следующим образом:

= - iK ц V 1 ( У ) - iK n U 2 ( ^ ) ,                      (4)

^dV 1        Ji   sin ² 6

—— = -iKе1 1--- ^U1 (у) + dу       [  це-nn

*2 J n sin 0 +iK in          * 'V2 («), | це-nn dU2        li sin2 0

= iK ц i 1--- ^{: d у}        | це - nn

V 2 ( У ) -

-

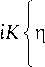
- nsin2 0 це-nn

’U1(У), dV

² = iK е U 2 ( У ) + iK n V 1 ( У ) • d у                         ^x

Запишем систему уравнений (4) в более ком- пактной форме:

dU T = A 1 ( У , ^K ) V 1 ( у ) + A 2 ( у , K ) U 2 ( у ) , ^{d у}

V = A 3 ( У , ^K ) U 1 ( У ) + A 4 ( У , ^K ) V 2 ( У ) , ^{d у}

U = A 5 ( У , ^K ) V 2 ( У ) + A 6 ( У , ^K ) U 1 ( У ) ,

A 6 ( У , ^K ) =

= - iK jn * ( У , K )

n ( y , K ) sin ² 0

ц ( У , K ) е ( у , K ) -п ( У , K ) n * ( У , K )

A 7 ( У , K ) = iK е ( у , K ) ; A 8 ( у , K ) = iK n* ( У , K ) •

Для системы уравнений (5), исходя из условий непрерывности тангенциальных составляющих напряженностей электрического и магнитного полей на границах раздела сред, запишем следующие граничные условия для случая волны горизонтальной поляризации:

U 1 ( 0 ) = 1 + R ee , U 2 ( 0 ) = - R eh cos 0 ,                 (6)

V 1 ( ⁰ ) = ( ¹ - R ee ) cos ⁰ , V 2 ( ⁰ ) = - R eh ,

U 1 ( ¹ ) = T ee , ^U 2 ( ¹ ) = T eh cos ⁰ ,

V 1 ( ¹ ) = Z ⁰ T ee cos ⁰ , V 2 ( ¹ ) = - | ° T eh •

Граничные условия для случая вертикальной поляризации представляются в следующем виде:

^U 2 ( ⁰ ) = ( ¹ - R hh ) cos ⁰ , U 1 ( ⁰ ) = R he ,                ⁽⁷⁾

• V 2 ( ⁰ ) = - ( ¹ + R hh ) , V 1 ( ⁰ ) = - R he cos ⁰ ,

^U 2 ( ¹ ) = T hh cos ⁰ , U 1 ( ¹ ) = T he ,

• V 2 ( ¹ ) = - Z ⁰ T hh , V 1 ( ¹ ) = - Z ⁰ T he cos ⁰ •

В соотношениях (6) и (7) Ree, Reh - коэффициенты отражения основной и кросс-поляризованной волн в случае горизонтальной поляризации; Tee, Teh – коэффициенты прохождения основной и кросс-поляризованной волн в случае горизонтальной поляризации; ZL – характеристическое сопротивление во второй области; Rhh, Rhe - комплексные коэффициенты отражения основной и кросс-поляризованной волн в случае вертикальной поляризации; Th, The - комплексные коэффициенты прохождения основной и кросс-поляризованной волн в случае вертикальной поляризации. Отметим, что соответствующий выбор величины импеданса ZL позволяет проводить расчеты для слоя на поверхности металла.

Как видно из соотношений (6) и (7), при решении

dU ₁

dV ₁

IT

£= 0

£ 0

dU ₂ d £

dV ₂ d £

= A i ( 0, K ) V i ( 0 ) + A 2 ( 0, K ) U 2 ( 0 ) ,

= A 3 ( 0, K ) U i ( 0 ) + A 4 ( 0, K ) V 2 ( 0 ) ,

= A 5 ( 0, K ) V 2 (0) + A 6 ( 0, K ) U i ( 0 ) , £= 0

= A 7 ( 0, K ) U ₂ (0) + A 8 ( 0, K ) V 1 ( 0 ) . £= 0

учтена кросс-поляризация поля, возникающая при падении электромагнитной волны на кираль-ный слой.

Повторно дифференцируя исходную систему (5) и подставляя в нее уже найденные значения полей и их производных (7), можно определить значе-

Входящие в выражения (4) материальные пара-

метры кирального метаматериала являются нор-

мированными и имеют вид

ния производных сколь угодно высокого порядка в точке £ = 0, выраженные через коэффициенты отражения. Предполагается, что нормированные

^S ( ^£ , K ) = S _C

+        ^Q _e K p _e . ( £ ) .

⁺ K ? _e3 Ю- K ² + iK Y ^K

ц ( £ , K ) = Ц _С

+ "K ;

K 2 .. ( £ ) - K ² + iK Y ^K

поля их производные вплоть до n -порядка являются непрерывными функциями координаты £ . Зная значения функций нормированных напряженностей полей и всех их производных в точке £ = 0, представим каждую из них рядом Маклорена:

X(A K ) =

» , K ,..    K

K 2 .. и- K ² + iK y K'

^U i ( £ ) = ^U i ( ⁰ )

+ U© £+ U^ £ 2 + . + i!             2!

Здесь K = o L/c , K _y =y L/c , K _pe3( £ ) = ro _pe3( £ ) L/c -нормированные волновые числа.

+ ^ £ k +.

£ £ 1%) _£ k. k =    ^{k !}

2. Методика вывода аналитических выражений для коэффициентов отражения

Рассмотрим методику получения аналитических выражений для коэффициентов отражения для случая слоя из неоднородного невзаимного кирального метаматериала. Пусть известны электрофизические параметры кирального слоя с координатными зависимостями относительных диэлектрической и магнитной проницаемостей, а также параметра киральности. Кроме того, из системы граничных условий (6)–(7) можно определить значения нормированных полей в точке £ = 0, выраженные через искомые коэффициенты отражения. В этом случае, применяя непосредственную их подстановку в систему обыкновенных дифференциальных уравнений (5), можно получить значения первых производных нормированных полей в точке £ = 0, также выраженные через коэффициенты отражения:

^U 2 ( £ ) = ^U 2 ( ⁰ )■ + U ²^ £ k +

^U 2 ( ⁰ k ^U 2 ( ⁰ )

i!              2!

Y ^U 2 ^k ) ( ⁰ )

=w

£ ² ++

£ ^k ;

^V i ( £ ) = ^V i ( ⁰ )

k = 0

+ V M £ +

V ^ £ 2 + . + 2 !

+ V B0) £ k ₊.

^V 2 ( £ ) = ^V 2 ( ⁰ )

= f ^V i ⁽ k ) ( ⁰ ) _£ k. ^w k !     ;

k = 0

+ V W £+ ^ £ 2 + . + i!              2!

+ V ^ £ k ₊.

£ V %) _£ k k 5 ^{k !}

При £ = i из соотношения (8) следует:

Ui (1)=Ui (0) +Uk^+...

₊ ^U i ( ⁰ ) ₊ U M _{+ +} i!       2!      .

v U i ^k ) ( 0 ) w ^{k !} ;

, .      , . и ‘ ( 0 ) и ;( o )

U 2 ( 1 ) = U 2 ( ⁰ ) + 4 + ^ ⁺ - ⁺

₊ U 2 k ) ( ⁰ ) ₊.

да

-z k-0

U2k)(0).

k !

Для случая падающей на планарный слой волны вертикальной поляризации из (7) и (9) получаем два линейных алгебраических уравнения относительно искомых коэффициентов отражения R hh , R he :

V 1 ( 1 ) = V 1 ( ⁰ ) ₊ V 1 ^{( k )}( ⁰ ) +..

V 2 ( 1 ) = V 2 ( ⁰ )

Vk)(0)

+ ——— + —

V’(0)M

+——— +——+—+

1!

V V ^M

' z k!'

V K 0 )   V ₂"( 0 )

i+—  + —+

1!

да z k - 0

U ⁽ k ) ( 0 ) k !

да z k - 0

vj^{k )}( 0 ) k !

—

ZL

Z ₀ cos 0

₌ Z fl⁰) ^{z k !}

.

Правые части уравнений системы (9) представляют собой линейные функции искомых коэффициентов отражения R ee >  R eh и R hh >  R he > а значения левых частей каждого из уравнений определены из системы граничных условий (6)–(7)

соответственно.

Для случая падающей на планарный слой волны горизонтальной поляризации из соотношений (6) и (9) получаем два линейных алгебраических уравнения относительно неизвестных коэффициентов

отражения ^, R eh :

да z k - 0

u 1 ^k ) ( ⁰ ) k !

да z k - 0

V k ) ( 0 ) k !

ZL

Z 0 cos 0

да z k - 0

U 2 k ⁾( 0 ) k !

Z_L cos 0

да z k - 0

U 2 ^k ) ( 0 ) k !

Zl cos 0

да z k - 0

1 ^0) k !

Z0

Для вывода приближенных аналитических выражений коэффициентов отражения достаточно взять некоторое конечное число членов слагаемых в суммах слева в соотношениях (10)–(11) и выразить из полученных уравнений искомые коэффициенты отражения.

да z k - 0

V R⁰) k !

Z0

В данной статье был представлен метод приближенного расчета коэффициентов отражения электромагнитной волны от слоя неоднородного невзаимного кирального метаматериала с учетом дисперсии материальных параметров. Показано, что использование предлагаемого аналитического подхода может существенно упростить процесс анализа взаимодействия электромагнитных волн с метаматериалами, обеспечивая при этом требуемую точность результатов. Применение предложенного метода позволяет быстро и эффективно оценивать характеристики отражения волн, что особенно важно в условиях ограниченного времени.

SPIN-код (eLibrary) : 9999-0844

AuthorID (eLibrary) : 649577

ResearcherID (WoS) : AAT-1882-2020

SPIN-код (eLibrary) : 2741-3794

AuthorID (eLibrary) : 34872

ResearcherID (WoS) : B-7134-2018

AuthorID (eLibrary) : 1115491

Physics of Wave Processes and Radio Systems

2025, vol. 28, no. 2, pp. 9–15

UDC 537.86                                                                                            Accepted 29 January 2025

Original Research                                                                                        Published 30 June 2025

Method for approximate analytical calculation of electromagnetic wave reflection coefficients from a layer of inhomogeneous non-reciprocal chiral metamaterial taking into account dispersion of material parameters

Dmitry N. Panin © , Oleg V. Osipov © , Yuliya S. Mamoshina

Povolzhskiy State University of Telecommunications and Informatics

• 23, L. Tolstoy Street,

  Samara, 443010, Russia

Е^И © Dmitry N. Panin et al., 2025

Dmitry N. Panin, Candidate of Physical and Mathematical Sciences, head of the Department of Theoretical Foundations of Radio Engineering and Communication, Povolzhskiy State University of Telecommunications and Informatics, Samara, Russia.

Research interests : theory of wave processes and computer modeling in radiophysics.

SPIN-code (eLibrary) : 9999-0844

AuthorID (eLibrary) : 649577

ResearcherID (WoS) : AAT-1882-2020

Oleg V. Osipov, Doctor of Physical and Mathematical Sciences, head of the Department of Higher Mathematics, Povolzhskiy State University of Telecommunications and Informatics, Samara, Russia.

Research interests : electrodynamics of metamaterials, antennas and microwave devices, nonlinear optics.

SPIN-code (eLibrary) : 2741-3794

AuthorID (eLibrary) : 34872

ResearcherID (WoS) : B-7134-2018

Yuliya S. Mamoshina, postgraduate student of the Department of Theoretical Foundations of Radio Engineering and Communications, Povolzhskiy State University of Telecommunications and Informatics, Samara, Russia.

Research interests : infocommunication networks, electrodynamics of metamaterials, theory of electrical circuits.

AuthorID (eLibrary) : 1115491