Метод продольных сечений для расчета собственных волн экранированных волноводов со сложным профилем поперечного сечения
Автор: Бударагин Р.В.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 1 т.19, 2016 года.
Бесплатный доступ
Предложен метод, который может быть использован для расчета собственных волн экранированных волноводов с произвольным законом изменения параметров волновода от поперечной координаты. Получена однородная система линейных алгебраических уравнений, к которой сводится решение рассматриваемой задачи. Проведена апробация метода на примере частично заполненных экранированных волноводов.
Собственные волны, ортогональный базис, экранированный волновод, диэлектрическая неоднородность
Короткий адрес: https://sciup.org/140255949
IDR: 140255949
Текст научной статьи Метод продольных сечений для расчета собственных волн экранированных волноводов со сложным профилем поперечного сечения
Для волноводов с однородным или частичным диэлектрическим заполнением, вписывающимся в ортогональную систему координат, полный спектр собственных волн определен и достаточно хорошо изучен [1–4]. Наибольшее распространение при решении задач такого типа получил метод частичных областей с ортогональностью собственных функций, образующих базис, по которому раскладываются компоненты электромагнитного поля собственных волн рассматриваемых волноводов. Но иногда не удается сформулировать в каждой частичной области краевую задачу Штурма – Лиувилля, а следовательно, невозможно определить базис собственных функций. Использование же в методе частичных областей представления полей в форме непрерывного спектра [5; 6] значительно осложняет задачу.
Для неоднородных волноводов со сложным, в общем случае плавным и многосвязным, профилем диэлектрического заполнения нахождение собственных волн является задачей еще более сложной. Подход, основанный на методе Галер-кина [7], на практике легко реализуется в случае, если форма ограничивающей поверхности соответствует какой-либо канонической системе координат.
В предлагаемой статье в качестве базиса для собственных волн неоднородного по поперечно- му сечению волновода используются поля собственных волн планарных диэлектрических волноводов, подробно исследованных в [2].
Метод не накладывает ограничений на закон изменения геометрических и диэлектрических параметров исследуемой структуры, а следовательно, его можно использовать для расчета как ступенчатой нерегулярности, так и плавных изменений профиля поперечного сечения волновода путем аппроксимации ступенчатой структурой.
Метод приводит к однородной СЛАУ, порядок которой определяется количеством учитываемых в разложениях собственных волн, а также количеством отдельных неоднородностей, которыми аппроксимируется рассматриваемое сложное сечение.
-
1. Определение базиса
Сложное, в общем случае многосвязанное сечение рассматриваемого неоднородного волновода (рис. 1) разобьем на области, продольные по координате z . Каждая выделенная область (рис. 2), бесконечная по координате x и z , представляет собой плоскослоистый металлодиэлектрический волновод, собственными волнами которого являются TE- и TH-волны.
Введем систему координат ( x , y, z) так, как показано на рис. 3. Рассмотрим произвольную волну, распространяющуюся вдоль © Бударагин Р.В., 2016
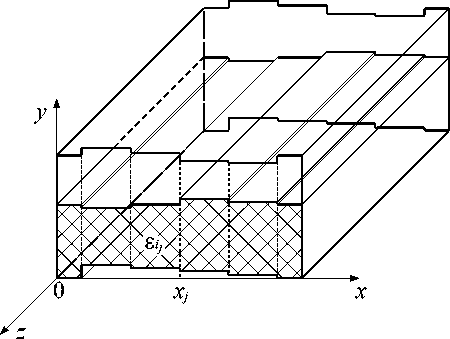
Рис. 1. Экранированных волноводов со сложным профилем поперечного сечения
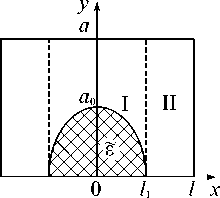
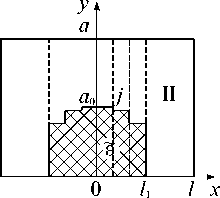
Рис. 3. Поперечное сечение экранированного эллиптического диэлектрического волновода и его ступенчатая аппроксимация
E x = E x cos ф = - г в х
х
I - 1
Z f i cos к У , у + f i sin к У , у i = 0 J
e - i к Х Хе - i в 2
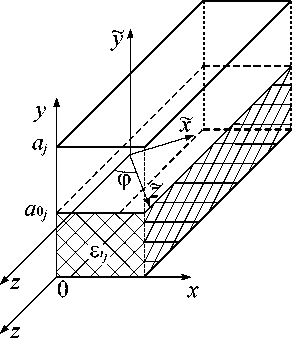
Рис. 2. Бесконечный плоскослоистый металлодиэлектрический волновод
E2 = - E x sin ф = i к Х х
х
I - 1
Z fi cos ^iy + fl sin ^iy i=0 ,
H x = H z sin ф =
к Х юц
оси 2 с продольным волновым числом в. Для
TE-волны, согласно [2], в каждой выделен-
ной
области j введем векторный
F- y
2 I - 1
Z f i cos к ' у i y + f i sin к у i y
I i = 0 J
e
- i e 2
.
потенциал
Для вол-
новых чисел к- и В выполняется соотношение yi к2Бij = ку2 + в2, где i = 0,1,..., I - 1 — номер слоя плоскослоистого волновода j; I – количество
/-V слоев в плоскослоистом волноводе; бij — от-
носительная диэлектрическая проницаемость i -го слоя j -й частичной области (б ij = Б ij Б о , Б о = 8,85 ■ 10 - 12 Ф/м). Поле TE-волны имеет три компоненты E , Н , Н .
xyz
Выберем систему координат ( x , y , z ) так, как показано на рис. 2. Пусть угол ф — угол между направлениями осей 2 и 2 . Обозначим через в = в cos ф, к Х = в sin ф. Волновые числа в рас-
сматриваемых системах координат связаны со отношениями: в2 = в2 + к^, к' = к’-,. Компоненты xyy поля TE-волны в системе координат (x, y, z) за-
пишутся:
„- i к' х - i в 2
e xe ,
I - 1
Z ^y.fi sin кУ,у- к'у1у;!' cos кУ,у х i=0 J
- i к'-т х„ х e х e
,- i р 2 ,
H y H y
- i
+ кх )
------- х юц
х
I - 1
Z fi cos кУ<У + fi sin кУ;У i=0 у
H x = H z cos ф =
в юц
e - i к Х х е - i в 2
I - 1
Z KУlfisin кУ.У - к'ylfl cos ^у.У х i=0 J
х e - i K Х xe - i в 2 ,
E y
Так как в системе координат ( x , y , z )
имеет
три компоненты магнитного поля
волна
и две
компоненты электрического поля, то, согласно [2], такие волны можно классифицировать как продольно-электрические, или LE-волны, для которых справедливо следующее соотношение
к 0 Б ij = к Х + к У + в 2 .
Аналогично для TH-волны, потенциал
Г I - 1
A y = Z
a cos к у + a ‘ sin к,-.
i yiiy
введя векторный
~
У e
, - i в 2 ,
в системе координат ( x , y , z ) получим:
E x = E z sin ф = —— х ЮБ 0
х
У к .»
V i = 0
a
S- sin к y - к yiyi s ij
a i
/-V s ij
cos к y y х У
- i к x - i В z х e x e
E y = E y = i
к x 2 ) х
|
J E ( j ) l ij ( j ) |
® [ 3 ( j ) = У A ( jj ) J En У n I H ( j ) n = 1 l2 x n |
( j ) - i к ( j ) x VO - e xn e - i в z + |
|
|
® [ 3 ( j ) + y F < j ) J E - n У n I H ( j ) n = 1 l - n |
( j ) i к ( j ) x - e xn e - i в z , |
||
х
ЮБ о
E a j
— cos кy y + eM
V i = 0 ij
a i
Уsin к y i . e
£ ij
У
- i к x - i В z xe ,
E z = E z cos ф = —— х ЮБ 0
х
У к .»
V i = 0
a
Ts sin к y y -к, s ij
yi
a i
/-V s ij
A
cos к y y х У
- i к x - i В z х e x e
H x = H x cos ф = Г I - 1
где An ( j ), Fn ( j ) – неизвестные амплитудные коэффициенты волн; к ^ ) — поперечные постоянные распространения LM-волн и LE-волн для j -й выделенной области; в — продольная постоянная распространения этих волн и собственной волны волновода со сложным профилем. Неизвестные волновые числа к ^ ) и в, связанные уравнениями (2) и (4), находятся из решения задачи. Векторные функции E ± jn , H ± n , описывающие поперечные (к оси x ) компоненты электрического и магнитного поля собственных волн плоскослоистых
областей, определяются как
= P У a i cos к y i y + a i sin к y i y e
V i = 0
H x = - H x sin ф = - i к x х
х
^ I - 1
У a i cos к y i y + a i sin к y i y
Hy = 0.
,- i к x x e - i P z
„ - i к x - i В z e xe ,
f E LM ( j ) . 3 + E LM ( j ) . k 1 E ( j ) J y ± n z ± n
±n | ELE(j). k l z ± n J f HLM(j). k 1
J ( j ) = J z ± n
± n |hle(j).3 + HLE(j). k l y ± n z ± n
Такие волны можно классифицировать продольно-магнитные, или LM-волны, для
как
ко-
торых справедливо следующее соотношение
k^ij = к ж + к у + P 2 . (4)
Амплитудные коэффициенты f i , f i , a i , a i и поперечные волновые числа к . , к y. определяются из равенства тангенциальных составляющих электрического и магнитного полей волны номера n (или n -й волны) на границах диэлектрических слоев плоскослоистого волновода j ,
Знак «–» при n в (5)–(6) означает, что соответствующая LM n -, LE n -волна распространяется против оси x .
Из условия непрерывности тангенциальных компонент поля на каждой границе раздела x = x j между волноводами j и j' = j + 1 получаем систему линейных функциональных уравнений:
N
У A kj ) ( E ( j ) . j + E ( j ) . k ) e ynzn
n = 1
- i к ( j ) Д x x n
-
а также из равенства нулю тангенциальных составляющих электрического поля на металлических поверхностях экрана при y = a 0 j ) и y = a ( j ) (рис. 3).
N
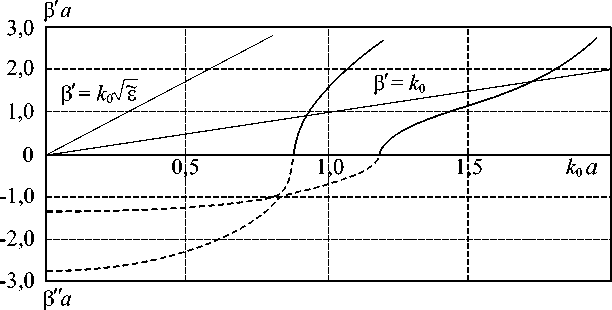
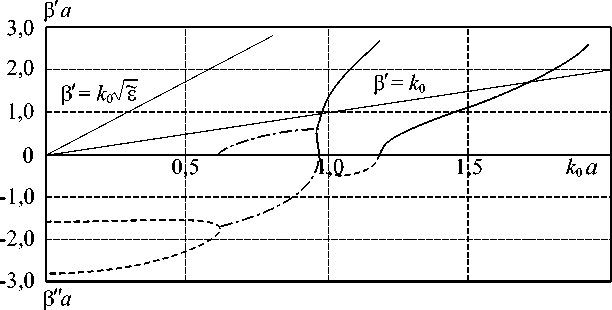
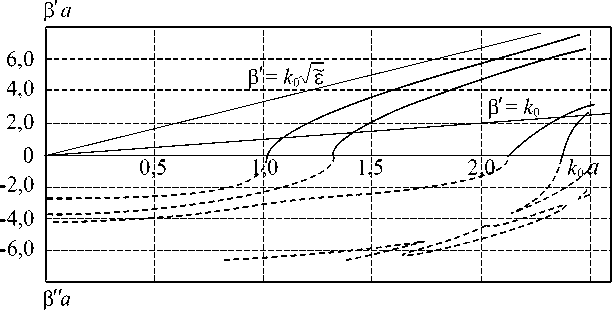
- F i к(j) Д x xn Sj N = У A< j+1)(E(j+1) . 3 + E(j+1) . k) -ynzn n=1 2. Описание метода В предлагаемом методе поперечное сечение неоднородного волновода (рис. 1) разбивается на области (регулярные вдоль оси z плоскослоистые волноводы). В каждом получаемом таким образом регулярном волноводе j электромагнитное поле представляется набором прямых и обратных по оси x собственных волн с неизвестными амплитудными коэффициентами: - N У F(j+1)(E(j+1) . 3 + E(j+1) n ynzn n=1 N У аПj)(H(j) . 3 + H(j) . k)e ynzn n=1 N - ■ k) Sj - i к( j) Д x xn + + F i к(3) Д x xn Sj N = a Рис. 4. Дисперсионные зависимости собственных волн экранированного эллиптического диэлектрического волновода с Al/a = 0,8, a0/a = 11 /a = 0,6 Рис. 5. Дисперсионные зависимости собственных волн экранированного эллиптического диэлектрического волновода с A l/a = 0,55, a0/a = 11 /a = 0,6 Рис. 6. Дисперсионные зависимости собственных волн экранированного эллиптического диэлектрического волновода с A l/a = 0,4, a0 /a = 11 /a = 0,6 N + YFj+1)(H(j+1) ■ j + H(j+M , ynzn n=1 Sj где N – количество учитываемых LMn- и LEn-волн в j и j' = j + 1 выделенных областях. Систему (7) необходимо решать при соответствующих граничных условиях в сечениях x = 0 и x = l. Умножаем первое уравнение (7) векторно на (H(j) ■ j + H(j) ■ к), а второе уравнение — на yqzq (E(j+1) ■ j + E(j+1) ■ к) и интегрируем полученные yqzq равенства по продольному сечению соответ- ствующего волновода Sj . Используя условие ортогональности собственных волн плоскослоистых волноводов, получаем систему однородных алгебраических уравнений второго рода относительно неизвестных коэффициентов разложения АПj), Fnj), которая в матричной записи имеет вид 5 ■ X = 0, (8) где XT =|^ A(0)D(1)F(1) ... D(j) F(j) ... F(J+1) J – вектор-столбец; ■ y(°) - W(0) - W(0)T ¥'(0) - E 5 — 0 0 : 0 0 _ 0 0 - W(0)^(1) 0 ^(1) 0 ^(j) E - W(j) W(j) T ^(j) - W(j)T - E 0 0 0 0 0 0 0 0 0 0 - W(j )^(j+1) 0 ^(j+1) 0 ^(J) E - W(J )¥(J+ W(J) T ^(J) - W (J) T -^'(J+1) E – единичная матрица с элементами Enq — 8 nq (8 nq — символ Кронекера); A(j), F(j) – векторы-столбцы амплитудных коэффициентов; W(j) – матрицы с элементами W(j)n = [ (e(j+1)H(j) - E(j+1)H(j)) ds; WT означает q,n yqznzqyn Sj транспонирование матрицы; ^(j) — диагональ-(j) - i K( j) Ax ная матрица, элементы которой ^„ n = e xn учитывают набег фазы волны с номером n. Здесь всюду j — 0,1,..., J, n = 1,2,..., N, q — 1,2,..., N. Приравнивание к нулю определителя матрицы S и дает искомую дисперсионную зависимость постоянной распространения волны в от частоты to. 3. Численные результаты Проведен расчет экранированного эллиптического диэлектрического волновода б=12, поперечное сечение которого изображено на рис. 3. Структура симметрична относительно плоскости x — 0, поэтому рассматриваем только ее половину (x > 0), которую разбиваем на области. Поля в областях представляются в виде суперпозиции собственных LM- и LE-волн плоскослоистых волноводов, образующих каждую частичную область. Компоненты полей в разложении (5) опреде- ляются из векторных потенциалов, которые для двухслойных областей запишутся в виде (I) (I) a cos к y 0n y0n A(I) = e-iPz есб(к® x) j ynxn – для LMn , при 0 < y< ao, a(I) cos к® (y - a) n y1n при a о < y < a f ((I) sin к'® y J 0n У о ny F(I) = e-iPz sin(K(I)x) j ynxn при 0 < y < a о, f(I) sin K‘(I) (y - a) 1n y1n при a о < y < a — для LE , где k(I) , k(I) , k'(I) , k'(I) — волновые д n , д у о n , Ут n ’ у о n ’ Ут n числа по координате y в соответствующих слоях определяются из достаточно простых дисперсионных уравнений [2]. Векторные потенциалы для области II запи- шутся в виде A(II) = e iPz sin k(ii) (x - l) x ynxn x a0II) cos к®) y, при 0 < y < a – для LMn , F(II) = e-iPz cos K‘(II) (x - l) x ynxn x f*11) sin ку11)y, при 0 < y < a - для LEn , где к (II) _ nn (II) _ —---, к — y0n a y0n п (n + 1) a вол- новые числа по координате y. В однородной области II электромагнитное поле собственной волны определяется через функции, которые совпадают с собственными функциями задачи Штурма – Лиувилля для этой области. Векторные потенциалы записываются так, чтобы обеспечить условие магнитной стенки при x — 0 и электрической стенки при x — l. Используя условия непрерывности тангенциальных компонент полей на границах раздела областей и условие ортогональности собственных волн стыкуемых волноводов, получаем систему линейных однородных алгебраических Рис. 7. Дисперсионные зависимости собственных волн экранированного эллиптического диэлектрического волновода с A^а = 0,002, а0/а = 11 /а = 0,6 уравнений (8). Приравнивание к нулю определителя системы позволяет выявить направляющие свойства рассматриваемого волновода, представленные на рис. 4–6 в виде зависимостей нормированных постоянных распространения Р а = (Р' + i Р") а от нормированной частоты , to «0а = — а, с - скорость света в вакууме. c На рис. 4 показаны дисперсионные зависимости первых двух волн рассматриваемой экранированной структуры (рис. 3). Также на этом рисунке штрих-пунктирными линиями изображены дисперсионные зависимости при отсутствующих боковых стенках экрана. Из рис. 4 видно, что все кривые поверхностных волн полуоткрытой структуры ограничены снизу прямой Р' = «0, ниже которой эти волны (начиная со второй) переходят в вытекающие. Из рисунка также видно, что сплошная и штрих-пунктирная зависимости для второй волны совпадают в области Р' > «0, что свидетельствует о слабом влиянии боковых стенок экрана на поле волны. Напротив, для первой волны это влияние значительно, так как при отсутствии боковых стенок эта волна не имеет отсечки. На рис. 5, 6 показана трансформация дисперсионных зависимостей первых двух волн рассматриваемой экранированной структуры при уменьшении расстояния Al = l - li от границы диэлектрика до боковых стенок экрана. Особый интерес вызывает трансформация кривых Р в области мнимых значений, проявляющаяся в появлении на этих кривых резких изломов (рис. 5) и в последующем переходе к комплексным решениям (рис. 6), которые изображены штрих-пунктиром. В тех случаях, когда значения Al становятся очень малыми (рис. 7), двузначные участки, равно как и комплексные волны низших типов, исчезают. Следует отметить, что многие из описанных явлений происходят при таких значениях Al, которые сравнимы с допусками изготовления диэлектрической вставки. Поэтому возникает вопрос о влиянии столь значительных трансформаций в дисперсионных кривых на интегральные характеристики устройств, которые могут изготавливаться на основе волноводов с такими вставками. Заключение В описываемом в статье методе расчета волноводов со сложным поперечным сечением предлагается рассматривать поле волн, распространяющихся в таких волноводах, как результат дифракции собственных волн планарных частично заполненных волноводов на поперечных неоднородностях. В случае однородно заполненных волноводов этот метод совпадает с методом частичных областей, когда поле в каждой частичной области представляется суперпозицией собственных функций краевой задачи Штурма – Лиувилля. Предлагаемый в статье метод может стать основой машинного проектирования функциональных узлов миллиметрового и субмиллиметрового диапазона длин волн. Метод не накладывает ограничения на закон изменения профиля поперечного сечения, что позволяет значительно увеличить номенклатуру линий передачи рассматриваемых диапазонов.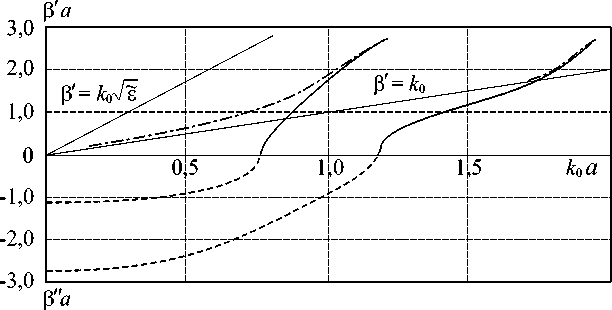
Список литературы Метод продольных сечений для расчета собственных волн экранированных волноводов со сложным профилем поперечного сечения
- Веселов Г.И., Раевский С.Б. Слоистые металло-диэлектрические волноводы. М.: Радио и связь, 1988. 248 с.
- Егоров Ю.В. Частично заполненные прямоугольные волноводы. М.: Советское радио, 1967. 216 с.
- Волноводы с поперечным сечением сложной формы / под ред. В.М. Седых. Харьков: Вища школа, 1979. 128 с.
- Волноводы сложных сечений / Г.Ф. Заргано [и др.]. М.: Радио и связь, 1986. 124 с.
- Раевский С.Б. Решение внутренних задач электродинамики с использованием непрерывного спектра в одной из частичных областей // Изв. вузов СССР. Сер.: Радиоэлектроника. 1980. Т. 23. № 9. C. 27-32.
- Новоселова Н.А., Раевский С.Б., Седаков А.Ю. Использование непрерывного спектра в методе частичных областей // Антенны. 2014. № 9 (208). С. 70-74.
- Титаренко А.А. Применение спектрального метода к расчету дисперсии волн регулярных волноводов с произвольным диэлектрическим заполнением // Физика волновых процессов и радиотехнические системы. 2013. Т. 16. № 3. С. 86-91.


