Метод прогноза и коррекции для моделирования автоколебательных систем

Уравнения движения нелинейных осцилляторов (колебательных и автоколебательных систем), как правило, не имеют аналитических решений. Поэтому теоретический анализ нелинейных колебаний часто основан на использовании приближенных асимптотических методов [1; 2] или методов численного интегрирования задачи Коши для систем дифференциальных уравнений [3; 4]. Не пытаясь дать развернутую характеристику последних, отметим, что они в большинстве случаев являются следствиями формальных аппроксимаций интегродифференциаль-ных операторов уравнений движения конечными разностями [5]. В связи с этим с практической точки зрения интересны алгоритмы численного моделирования нелинейных динамических систем, базирующиеся на физических представлениях о протекающих в них процессах.

В настоящей статье описан метод прогноза и коррекции для моделирования нелинейных колебательных и автоколебательных систем томсоновского (резонансного) типа. Метод основан на использовании дискретной временной модели линейного резонатора (ДВ-осциллятора) в качестве основного динамического элемента системы. Нелинейности и обратные связи вводятся в ДВ-осциллятор способом структурного синтеза [6].

1. Вариант схемы прогноза и коррекции для колебательных систем

Значительное число нелинейных динамических систем можно описать дифференциальной моделью вида

d ² x to o dx dt ² Q dt

+ to o x — to o F

^dx ) t , x , — I, dt J

где to o и Q - собственная частота и добротность линейного осциллятора, входящего в состав системы. Функция F ( ■ ) учитывает обратные связи и нелинейности системы. Предполагая в дальнейшем численное интегрирование задачи Коши для дифференциального уравнения (1) с шагом А, введем в уравнение безразмерную временную переменную т — t / А и запишем его в виде

d2x    dx 2222

—-—+ 2nv    + 4п Оqx — 4п О0F (т, x, у).(2)

d т2

Здесь О о — to o / to d — собственная частота, измеряемая в единицах частоты дискретизации to d — 2п / А; v — O o / Q - полоса резонатора. Временную производную осцилляций в (2) учитыва-

ет переменная

у (т) —

1 dx

2nO o d т

Рассмотрим «физически обоснованный» подход к разработке алгоритма численного интегрирования уравнения (2). Основным его положением

является требование о сохранении импульсного отклика h (т) линейного осциллятора, описываемого левой частью (2), в ходе временной дискретизации. При этом правую часть уравнения (2) формально предлагается считать внешним воздействием на осциллятор: f (т) = F ( т, x (т), у (т) ) .

Импульсный отклик (импульсная характеристика) осциллятора определяется уравнением d-h + 2nv — + 4n²Q 2 h = 4л²П 2 5(т).

d т²        d т         0          0

Более точную центральную разность предлагается использовать в комбинации «прогноз – коррекция», определив ее через прогнозируемое ( p )

значение x_n как

( p )

y n - 1

( p ) n

^{- x}n - 2

4nQ0

Полученная в рамках такого подхода схема прогноза и коррекции выглядит следующим образом:

x (p) - 2a cos ( 2nQ 0 ) x n - 1 + a² x n - 2 =

Последовательность отсчетов h_n = h (т _n ) на временной сетке т _n = n формирует импульсную характеристику линейного осциллятора в дискретном времени:

h n = 2kQo exp ( -nv n ) sin(2nQ₀ n ), n = 0,1,2,...

Дискретное во времени преобразование Фурье (ДВПФ) последовательности (3) определяет ча- стотную характеристику

H ( j Q) =

2nQ₀a sin(2nQ₀) W ( j Q )

1 - 2a cos(2nQ₀) W ( j Q ) + a² W ( j 2Q ) ’

где W ( j Q ) = exp(- j 2nQ) — множитель задержки; a = exp(-nv) — множитель затухания.

В частотной области последовательности от- счетов осцилляций на выходе xn = x(n) и входе fn = f(n) представлены спектрами (ДВПФ) X (jQ) и F (jQ) . Известно, что спектры входного и выходного сигналов линейной систе- мы связаны частотной характеристикой как

X ( j Q ) = H ( j Q ) F ( j Q ) . Поэтому на основании (4)

можно записать выражение

( 1 - 2a cos(2nQ₀) W ( j Q ) + a² W ( j 2Q ) ) X ( j Q) = = 2nQ₀a sin(2nQ₀) W ( j Q ) F ( j Q).

Применив к (5) обратное ДВПФ, нетрудно восстановить связь последовательностей x_n и f_n :

x n -2a cos ( 2nQ 0 ) x n - i + a² x n - 2 =

= 2nQ 0 asin ( 2nQ 0 ) f n - i .

С учетом того, что fn = F (n, xn, yn ), это равен- ство принимает вид xn-2a cos (2nQ0) xn-i + a2 xn -2 =

= 2nQ 0 asin ( 2nQ 0 ) F ( n - 1, x n - i , y n - i ) .

Способ аппроксимации производной y n - 1 в (6) определяет тип разностной схемы для сеточной функции x_n . Аппроксимация левой разностью

( l ) = ^xn - 1 ^{- x}n - 2

y n ^{- 1}      2nQ₀

позволяет получить простую явную схему, но имеет лишь первый порядок точности по Q 0 .

= 2nQ0asin (2nQ0) F (n - 1, xn-1, уn)-1), xn - 2a cos (2nQ) xn-1 + a2xn-2 =

= 2nQ 0 asin ( 2nQ 0 ) F ( n -1, x n - 1 , y n - 1 ) .

Теоретическая оценка точности разностной схемы (8) вызывает затруднения. Можно лишь отметить, что в работе [7] погрешность разностной аппроксимации дифференциального оператора в левой части уравнения (1) оценена как величина второго порядка малости. Также и погрешность разностной аппроксимации (7) 2 оценивается величиной, пропорциональной Q₀ . Поэтому, условно определив (8) как схему второго порядка, оценим ее точность на конкретном примере.

2. Пример: осциллятор Ван дер Поля

В принятых выше обозначениях классическую модель автоколебательной системы – осциллятор Ван дер Поля – можно определить уравнением dx + 2nv — + 4n2Q2x = 4n2Q2Y(1 - x2)у.      (9)

d т²        d т

Здесь параметр у характеризует глубину положительной обратной связи в системе. Он связан с параметром превышения порога генерации простым соотношением: p = у Q (порог генерации p = 1).

Для нелинейного осциллятора (9) схема прогноза и коррекции (8) имеет вид

x (p) - 2a cos ( 2nQ 0 ) x_n - 1 + a² x_n - 2 =

= yasin ( 2nQ 0 ) ( 1 - x n - 1 ) ( x n - 1 - x n - 2 ) ,

2                      (10)

x_n - 2a cos ( 2nQ ) x_n - 1 + a² x_n - 2 =

= 0.5yasin ( 2nQ 0 ) ( 1 - x n - 1 )( x n ) - x n - 2 ) .

Вычисления по (10) будем сопоставлять с вычислениями методами Рунге – Кутта четвертого порядка ( RK4 ) и Хойна (метод второ-

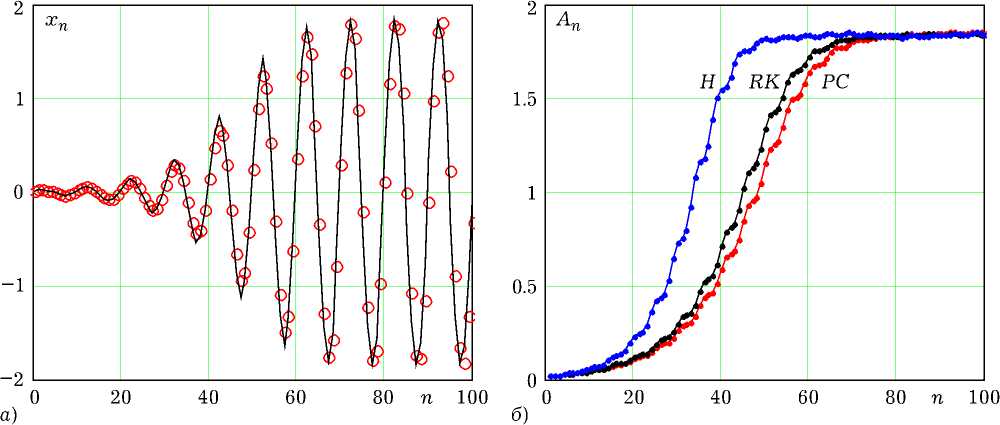
Рис. 1. Процесс установления автоколебаний

а)                                                             б)

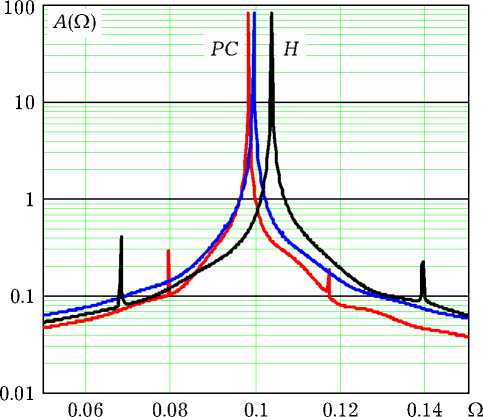
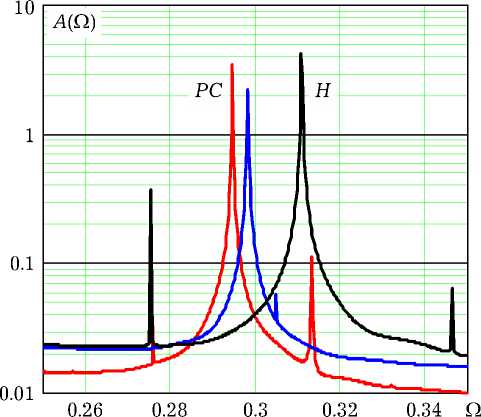
Рис. 2. Амплитудные спектры установившихся автоколебаний

го порядка). Метод RK4 , как наиболее точный, считается эталонным. При этом зафиксированы следующие значения параметров осциллятора Ван дер Поля: Q = 20 — типичное для автогенераторов значение; p = 7 — высокий уровень возбуждения; Qq = 0.1 — соответствует шагу интегрирования с десяти точками на период.

На рис. 1, а приведены графики процесса установления автоколебаний: точками отмечены значения x_n , рассчитанные по методу (10), непрерывной линией – по методу RK4 . Временные зависимости огибающих в процессе установления показаны на рис. 1, б : РС – метод прогноза и коррекции (10); RK – метод Рунге – Кутта; Н – метод Хойна. Выделение огибающих проведено методом аналитического сигнала с использованием дискретного преобразования Гильберта.

Как следует из графиков, в переходном режиме результаты метода (10) более близки к результатам метода RK4 , чем к результатам метода Хойна. При этом все три метода дают практически одно и то же значение амплитуды установившихся автоколебаний.

Сравнение частот автоколебаний, рассчитанных тремя методами, проведем в спектральной области.

На рис. 2 показаны амплитудные спектры A (Q) = | Х ( j Q)| установившихся автоколебаний в окрестности частоты первой ( а ) и третьей ( б ) гармоник. Спектральные оценки получены 4096-точечным дискретным преобразованием Фурье. Они демонстрируют близость частот автоколебаний, рассчитанных методами (10) и RK4 : Q rk = = 0.0981 ± 0.0001; Q(1q) = 0.0994 ± 0.0001. Причем

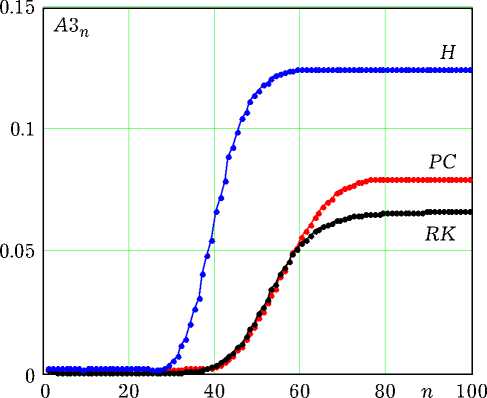
Рис. 3. Процесс установления амплитуды третьей гармоники эти частоты несколько ниже собственной частоты контура Ω0 = 0.1. Метод Хойна дает завышенное значение частоты: ΩH = 0.1035 ± 0.0001.

В качестве еще одной сравнительной характеристики методов можно использовать результаты генерации третьей гармоники автоколебаний. Временные зависимости ее амплитуды A 3 _n , рассчитанные тремя анализируемыми методами, показаны на рис. 3. Метод (10) дает завышенное по сравнению с RK4 значение. Но еще большее превышение демонстрирует метод Хойна.

Таким образом, результаты приведенного тестового примера дают основания считать, что предложенная схема прогноза и коррекции (8) имеет преимущества в точности расчетов перед стандартными методами второго порядка.

Заключение

Описанный здесь метод может быть полезен в численных экспериментах с нелинейными осцилляторами [8], в том числе при наличии шумовых воздействий [9]. В последнем случае, учитывая необходимость обработки большого числа реализаций стохастических колебаний, рассматриваются варианты использования методов невысоких порядков, вплоть до модификаций метода Эйлера (см., например, [10]). Метод применим также для моделирования автоколебательных систем с запаздывающими связями, например, таких, как генератор, исследуемый в работе [11].

Отметим также, что результаты спектрального анализа численных решений указывают на то, что высшие гармоники основной частоты нелинейных колебаний в процессе дискретизации времени могут быть подвержены эффекту под- мены частот [12]. Так как в спектре нелинейных колебаний в большинстве систем присутствует третья гармоника, в качестве одного из условий адекватности численной модели можно принять условие ее генерации без эффекта подмены. Это означает ограничение на шаг временной дискретизации в виде неравенства ω0∆≤π/3, следующего из неравенства 3Ω0 ≤ 0.5.