Метод расчета эволюции напряжений в стеклометаллокомпозите с учетом структурных и механических релаксационных процессов

Изучение возможности упрочнения стекла, входящего вместе со сталью в состав стеклометаллокомпозита, привело к созданию стержней, состоящих из стеклянного сердечника и стальной оболочки. Они изготавливаются методом припаивания стекла к стали в окислительной среде при определенном температурном режиме [1–3]. Технология их изготовления подразумевает получение так называемого сжатого спая со специальными прочностными характеристиками и в этих целях использует варьирование температуры, механических характеристик и структуры соединяемых материалов. Изменения служат причиной появления технологических напряжений, которые могут вызывать образование дефектов, разупрочняющих стеклометаллокомпозит. В свете этого актуальна разработка математической модели, прогнозирующей механическое поведение материала при колебании значений параметров технологического режима с учетом процесса стеклования и пластического течения в металле.

Явление стеклования, несмотря на большой накопленный экспериментальный опыт, не имеет общей теории, кроме гипотезы Г. Таммана, что стекло — это переохлажденная жидкость [4]. Тем не менее, теоретические исследования стеклования выделились из общей теории фазовых переходов в отдельное направление, вклад в развитие которого связывается с именами Александрова А.П., Лазуркина Ю.С. [5], Шмельцера Ю.В.П. [4, 7] Мазурина О.В. [6, 9, 10, 12], Старцева Ю.К. [8, 11], Тула А. [13], Нарайанасвами О. [14], Мойнихана К., Маседо П. [15] и других. Обзоры современного состояния теорий стеклования приведены в работах [4–6]. Неоднозначность походов к моделированию явления стеклования, как справедливо отмечает Старцев Ю.К. [7], приводит к ряду трудностей. Специалистам, занимающимся изучением свойств стеклообразных материалов, и технологам при изготовлении и эксплуатации приходится сталкиваться с непростой проблемой сравнительного анализа и выбора теории, в рамках которой будет выполняться решение актуальной научной и/или технологической задачи.

Разумным и эффективным при моделировании конкретного технологического процесса представляется выбор в пользу теоретического подхода, который апробирован экспериментально и близок по постановке задачи к исследуемой технологии и материалу. По результатам обзора методов математического описания технологических напряжений в стеклометаллокомпозитных стержнях было выбрано направление научной школы Института химии силикатов им. И.В. Гребенщикова АН СССР. Релаксационная теория стеклования и метод определения свойств стекол при переходе через фазу стеклования, разрабатываемые группой О.В. Мазурина [9–11], проверены на обширном экспериментальном материале, в том числе при отжиге спаев стекла с другими материалами [12]. В основе метода лежит идея А. Тула о введении в модель изменения структуры стекла в фазе стеклования структурного параметра, характеризующего состояние системы, — «фиктивной» температуры T _f . Параметр связан с приведенной изобарической теплоемкостью системы [13]. Аналогичный подход развивался за рубежом в работах Нарайанасвами О. [14], Мойнихана К. [15] (известен как ТНМ метод — метод Тула–Нарайанасвами–Мойнихана). В рамках релаксационной теории отжига спаев стекла с другими материалами разработаны методы расчета напряжений при температурной обработке, например, плоских вакуумноплотных двухслойных спаев стекла с металлом, которые эффективно применяются при расчетах напряжений в аморфных покрытиях [16, 17]. Справедливости ради считаем нужным использовать далее следующее сокращенное название метода: метод ТНММ — метод Тула– Нарайанасвами–Мазурина–Мойнихана. Существующие модели представления механических характеристик в спае, находимых по методу ТНММ, разработаны для плоских спаев и имеют следующие ограничения: опасными считаются растягивающие напряжения в стекле, поэтому контролируется напряженно-деформируемое состояние только в стекле (с целью предотвращения его разрушения), а эволюция напряженно-деформированного состояния металлических слоев не принимается во внимание, спаи считаются вакуумно плотными, поэтому на границе соединения стекла и металла предполагается идеальный контакт [12, 16, 17]. Похожие технологические задачи с учетом терморелаксационных переходов решаются в работах механиков пермской школы (см. моделирование конструкционной прочности силового кварцевого оптического волокна, неоднородно легированного по радиусу [18, 19], и полимерных материалов [20]) и в работах, опубликованных в зарубежных изданиях [21–24]. Между тем в стеклометаллокомпозитах в процессе изготовления возможно развитие упругопластического напряженно-деформируемого состояния (в металле), приводящегоиногда даже к разрушению металлического слоя при неправильно подобранных параметрах технологического процесса и размеров металлического слоя. Попытки описать изменение геометрии рассматриваемых спаев и упругопластическое деформирование металлического элемента спая требуют усложнения задачи и доработки метода ТНММ.

Целью данной работы является математическое моделирование и создание метода расчета эволюции напряженно-деформируемого состояния стеклометаллокомпозита с учетом как процесса стеклования и релаксации напряжений в стекле, так и пластического течения в металле.

2.    Постановка задачи

Температурный режим изготовления стеклометаллокомпозитных стержней (Рис. 1 а , б ) включает нагрев, охлаждение и последующий отжиг. На этапе нагрева стекло, доведенное до размягченного состояния, под действием приложенной нагрузки продавливается и плотно прилегает к внутренней поверхности металла. При охлаждении вязкость стекла возрастает, происходит процесс стеклования. Разница свойств соединенных стекла и металла приводит к значительным неравномерно распределенным остаточным напряжениям, для отслеживания которых необходимо осуществлять контролируемое охлаждение (отжиг). Обычно отжигу подвергается готовое изделие, которое дополнительно нагревается и затем охлаждается с разными скоростями. Стеклометаллокомпозиты отжигаются при изготовлении спая на этапе его охлаждения, поскольку существенное отличие механических характеристик соединяемых материалов ограничивает температуру повторного нагрева и заметно сужает температурно-временной интервал обработки изделия отжигом. Процесс отжига можно разделить на три последовательных операции (Рис. 1 в ): I — охлаждение от максимальной температуры T _max до температуры отжига T _от ; II — выдержка; III — охлаждение до температуры окружающей среды T _cр .

а

б                                в

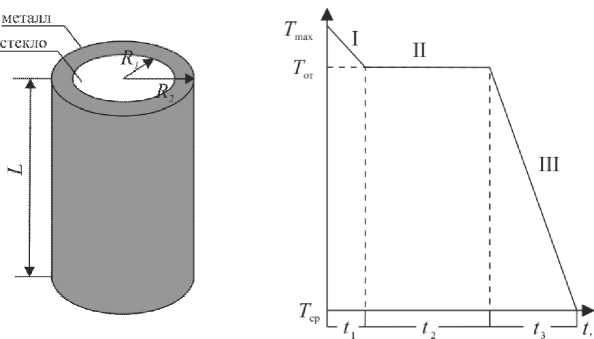
Рис. 1. Фотографии экспериментальных образцов из [3] (а); геометрия образцов (б); температурный режим отжига (в)

При охлаждении от температуры Tmax , которая может совпадать с температурой плавления стекла TI или быть несколько меньше ее, непрерывно изменяются структура и свойства стекла. Такой процесс называют стеклованием, и он протекает в некотором интервале (Tg , T^, одна из температур находится в его средней части и называется температурой стеклования — Tg . Ее положение зависит от скорости охлаждения, а границы интервала стеклования обычно соотносят с границами гистерезисной петли, характеризующей изменение свойства P при равномерном охлаждении и нагреве от равновесного состояния расплава к замороженной структуре (Рис. 2). Важным свойством, определяющим специфику стеклообразного состояния, является вязкость. Температуре стеклования Tg при различных составах стекла обычно соответствует температура при скорости охлаждения, равной 3 K/мин, и вязкость из диапазона 1013+1013,3 Па^с, температуре размягчения Tl — вязкость 4х(108+109) Па^с [11, 18, 25].

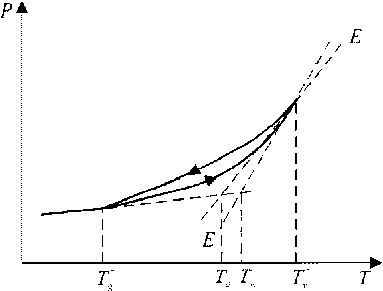
Рис. 2. Характер температурной зависимости изменения некоторого свойства стекла ( P ) при равномерном охлаждении и нагревании: T _g ‒ температура стеклования в режиме охлаждения, а T_w - в режиме нагрева; ( Е - Е ) -равновесная температурная зависимость свойства

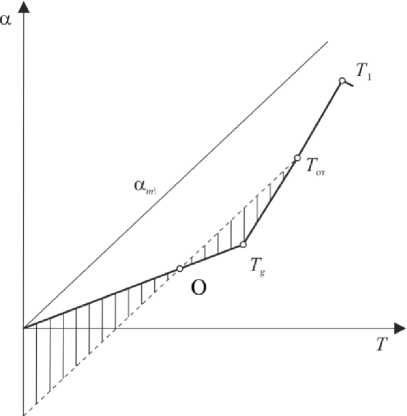
Рис. 3. Отжиг сжатых спаев металл–стекло, когда a m » а _g

При изготовлении стеклометаллокомпозита вследствие разницы линейных коэффициентов температурного расширения и модулей Юнга даже при равномерном распределении температуры возникают напряжения. Анализ зависимостей линейных коэффициентов температурного расширения стекла (аg) и металла (am) от температуры (Рис. 3) показывает, что в стекле при охлаждении возникают растягивающие напряжения, и только начиная от точки О напряжение меняет знак и становится сжимающим. Поэтому технологи рекомендуют выбирать режим отжига так, чтобы напряжения растяжения, возникающие при охлаждении, снижались, пусть даже за счет увеличения сжимающих напряжений [19]. Значит, температура отжига Tот должна быть близкой по значению температуре стеклования Tg , тогда точка О сместится в сторону более высоких температур. Поскольку стеклометаллокомпозиты получают в печах, режим их отжига необходимо отрегулировать таким образом, чтобы в области между Tl и точкой Tот скорость снижения температуры была наименьшей.

Кроме термического расширения, на образование напряжений существенное влияние оказывают размеры стеклянного и металлического цилиндров, изменение свойств стекла при переходе через интервал стеклования, а также возможность развития необратимых деформаций и пластического течения в металле. Учитывая все перечисленные особенности, рассмотрим задачу определения технологических и остаточных напряжений при отжиге стеклометаллокомпозитных стержней.

3.    Математическая модель

При математическом моделировании напряженно-деформированного состояния составного цилиндра (Рис. 1 б ) с разными механическими свойствами его частей (термовязкоупругого со структурными изменениями — во внутреннем стеклянном цилиндре, и термоупругопластического — в металлическом внешнем цилиндре) принимались следующие предположения:

– соблюдается температурный режим изготовления стеклометаллокомпозитных стержней, то есть они равномерно нагреваются, и изменение температуры имеет невысокую скорость, до 0,25°С/с (в работе [27] показано, что при определенных диаметрах ( d <  80 х 10 - 3 м) разница в изменении температуры по радиусу составляет 10^–2°С, что позволяет считать температурное распределение известным и одинаковым во всей расчетной области и соответствующим режиму изменения температуры Т ( t ) в среде (печи));

– в стеклянном компоненте преобразования структуры и колебания температуры приводят к изменению вязкости стекла и, соответственно, времени релаксации; для описания физико-механических явлений, связанных со стеклованием и структурной релаксацией, применима модель ТНММ;

– рассматриваются стержни с отношением диаметра к длине менее 1:10, при этом их торцы свободны от нагрузок; выполняется гипотеза об обобщенном плоском деформируемом состоянии ( е z = const);

– на границе соединения стекла со сталью соединение идеальное;

– материал металлического слоя идеально упругопластический (без упрочнения).

Базовым понятием модели ТНММ является «фиктивная» температура (fictive) T_f , которая в стабилизированном состоянии равна фактической температуре ( T ), в условиях замороженной структуры постоянна ( T_f = const), при равномерном охлаждении уменьшается вплоть до нижней границы интервала стеклования, минуя ее, далее остается постоянной [9, 13].

Фиктивная или структурная температура (температура, связанная со структурными изменениями в материале) в релаксационной теории имеет следующую математическую интерпретацию [14]:

Т = Тй + J (1 - Ms (£-£')) dTdS ,(1)

о

T ₀ — температура, от которой начинается охлаждение. Функция структурной релаксации свойств стекол хорошо описывается функцией Кольрауша [11, 21]:

Ms (S) = e:r)b = eK/nr)b,(2)

здесь b — постоянная величина для стекол определенных составов (0 <  b <  1), и вместо текущего времени t используется «приведенное» время S , которое, согласно методу температурно-временной аналогии [27], связано с текущим временем безразмерной универсальной функцией f ( Т ) соотношением d S = f ( t ) dt . Но обычно «приведенное» время выражают через сдвиговую вязкость или время релаксации свойств:

tt ^e( t ) = ! <) ^dt' или - ' t ) = ! w^dt'

где n r — вязкость сравнения (сдвиговая вязкость при произвольно выбранной температуре сравнения T r ), р ( t ) — текущая вязкость, т r — время релаксации при температуре сравнения, K r = р r /т r .

Изменение структурной температуры сказывается на изменении вязкости р и линейного коэффициента температурного расширения а через аналитические соотношения, предложенные в работах [9, 13]:

1g п = 1g П 0 + B e ( T f -” — T 0- 1) ) + B f ( T ') — T f -¹’) ,

а = a _e + ( а f

—

а e )( dT f/ dT ) ,

где п₀ — вязкость при T 0 , а B e , a _e , B_f , а f — коэффициенты, характеризующие температурные зависимости п и а в условиях равновесной и замороженной структур соответственно (Рис. 4).

В цилиндрической системе координат (см. Рис. 2) при осевой симметрии с учетом принятых предположений компоненты тензоров перемещений и деформаций представляются как ur = U (r, t), u ф= 0,   uz = w (z, t), du         u

⁸ rr    d r ’       ■ r ’

d w / \

8 =--= 8 u), £ =£ =£ = 0. zz d z\ /, r ф rz      ф z

Аналогично вводится тензор

напряжений,

имеющий три ненулевых компоненты ст _rr = ст _r ( r , t ) ,

ст =ст rt ст фф ф \ ,    , zz остается одно:

= ст z ( r , t ) из

уравнения равновесия при отсутствии массовых сил невырожденным

■ —ст

-----ф = 0.

r dCT r +CT 5r

Определяющие

соотношения

для 0 <  r <  R 1

(в стекле) могут быть описаны на основе принципа

суперпозиции Больцмана–Вольтерры [27]:

S r = 2 G e r —

s ф = 2 G | e ф —

S z = 2 G\e z —

t jM(n(t,t'))ed'I t,

■ jM (n(t, t))eфdt I, 0

t jM(n(t,t'))ezdt' I, 0

но, поскольку cтеклообразные материалы практически не обнаруживают объемных релаксационных свойств, их физическое поведение может быть представлено уравнением Дюамеля–Неймана:

ст ( r , t ) = 3 K 0 .

В (6) и (7) приняты обозначения: ст = ( ст _r + ст _ф + ст _z

T

= ( 8 r + 8 ф + 8 z )/з ; 9 = 3 8 — j a ( T ) dT ; s r =ст r —ст ,

5 =а — а: е =£ -s, е =8 ф ф ; r r , ф ф

—

T 0

8 , e_z =8 _z —8 ; G — модуль сдвига; K — модуль объемной деформации;

M ( п ( t , t ') ) — релаксационное ядро, характеризующее снижение к моменту времени t сдвиговых напряжений, вызванных деформацией в момент времени t' , аналитическая запись которого неэкспоненциального вида, принятого в (2), при этом параметры b и K_r отличаются от значений, используемых при отыскании структурного параметра T_f . Изменение структуры и температуры приводит к изменению вязкости п согласно формуле (3).

Для внешнего цилиндра ( R 1 <  r <  R 2 ) определяющие соотношения запишем в рамках модели Прандтля–Рейса с учетом тепловых явлений и разделением малых деформаций на обратимую (упругую 8 j ) и необратимую (пластическую 8 ^р ) составляющие (здесь и далее точка над символом означает дифференцирование по времени):

ep

⁸ ij    ⁸ ij ^{+ 8} ij

•

или 8

ep jj     ⁸ ij ^{+ 8} ij .

Упругое состояние в пространстве напряжений ограничим поверхностью предельного состояния Мизеса и условием активного нагружения f (°, T) = (°r — °^)2 + (o z — стф )2 + (CTr — °z)2 — 2° T ( T ) = 0, f-° д° r r

д f •

■ / ° r ^д° r

д f •     д f •   „

■    ° + — T > 0, д° r дT

предел прочности при растяжении ° _T (T ) зависит только от температуры. Пластические составляющие компонент тензора деформаций определим согласно закону ассоциированного течения:

⁵ f            ⁵ f            ⁵ f

sг V,   еф =Л^ ,   sz  Л/, д° r             д°ф             д° z здесь Л имеет смысл множителя Лагранжа при нахождении максимума удельной мощности деформирования с ограничением (9).

Учитывая соотношения (4) и (8), упругие деформации перепишем в виде:

s

e

r

д и

—

д r

s

p

r

,

s ;

u

—

s,

p

r

■ф

,

s \ = s zz

—

s:

p

z

.

Тогда напряжения и деформации в слое 0 <  r <  R_i будут связываться согласно формулам:

° r

° .

° z

Краевые условия установим исходя из условий отсутствия нагрузки на внешних поверхностях стержня и равенства радиальных напряжений и перемещений при переходе через границу стекла с металлом при идеальном контакте:

и ( R i — , t ) = и ( R i + , t ),       ° r ( R i — , t ) = ° r ( R i + , t ),

° r ( R 2 , t ) = 0,

L ^R ° z ⁽ r , t ) rdr ⁺ [ R ² ° z ⁽ r , t ) rdr = 0.

0                         R ₁

В начале процесса отжига считаем, что напряжения, перемещения и скорости их изменения во времени равны нулю:

и ( r ,0) = 0,      u( r ,0) = 0,

° r ( r ,0) = 0,      ° ( r ,0) = 0,      ° z ( r ,0) = 0,                              (13)

° r ( r ,0) = 0,     _ф(r ,0) = 0,     ° z (r ,0) = 0,     0 < r< Ri.

Используя соотношения (6), (7), уравнение равновесия (5) для цилиндра 0 <  r <  R _i можно переписать как

⁴ G + K

д ² и   i д и

+ д r   r д r

—

u r ²

2   r t ,,_xf д² и    i д и    и ] ,, „

— G M ( t , t ' ) —т +---- dt' = 0,

3   ^J0   ^V \д r ²    r д r  r ² J

в тоже время уравнение равновесия (5) для внешнего цилиндра R _i <  r <  R ₂ с учетом (ii) примет вид:

д ² и  i д и   и =     2 G     дs p  ^s p ^{— s} P

д r ²    r д r  r ²    ( 4 G / 3 ) + К^ д r r ^

Решением уравнений (14) и (15) (при упругом деформировании металлического слоя) является решение уравнения Эйлера:

ci¹ u   1 d u u _

—T +----= = 0, dr   r 5r  r u (r, t) = «

C 1 ( t ) r ,

C i ( t ) r + C ³ ( t ), r

0 <  r <  R„

R 1 <  r <  R ₂.

Здесь C 1 ( t ), C ₂ ( t ), C ₃ ( t ) и £ _z ( t ) — неизвестные коэффициенты, которые получаются из краевых условий (12). Пусть

^J Gg , Kg , ^ag , G , K , a = <  ^{g g g}

I ^G m , ^K m , ^a m ,

0 <  r <  R 1 , R 1 <  r <  R ₂.

Из соотношений (6) с учетом формул (4) и (16) имеем напряжения в явном виде:

( 2 G          3          (        7 A         2 G ,t    .      .                 .             ,t . .

a r = a , = I      + 6 K g I C 1 ( t ) +1 3 K g - ² G g I £ z ( t ) -      J M ( t , t ' )( C 1 ( t 3 - £ z ( t 3 ) dt ' - 3 K g J a g ( T ) dT ,

3             )           3          3 J             3 V0

Z 3                               X(18)

(         2 G I (         4 G I 2 G ,t    .      .                 .             ,t . .

a z = 2 | 3 K g - ,   I C i ( t ) + | 3 K g -  _   Is z ( t ) +   ,  J M ( t , t ‘ )( C i ( t 3 -£ _z ( t 3) dt '- 3 K g J a _t ( T ) dT .

3                3    J l                3    J                3   1,0

Соотношения (11) в упругой области с учетом (16) могут быть переписаны так:

a r =( 6 Km - 2 Gm | C2( t) - 2 Gm^ + (3 Km - 2 Gm \z (t) - 3 Km J" a m ( T ) dT , 3         3    J                  r      3         3    J a, = ( 6Km + 2 Gm IC2(t) + 2G C 1 t1 + ( 3K„ - 2 Gm | £z (t) - 3Km J T am (T) dT , 3         3    J                  r      3         3    J

T a = 2I 3Km — Gm IC (t) + 1 3Km + - Gm |sz (t) - 3Km [ a.(T) dT . z       m     m 2       m     mzm m

3          3 J          3          3 J

Введем новую неизвестную: C 1 ( t ) = C 1 ( t ) -£ _z ( t ) . В результате система (12) с учетом (16)-(19) примет вид:

С

^ ^ 1 +£ z = C 2 + -2 ,

R ₀

Ct

I 6 K m - - G m I C 2 ( t ) - 2 G m      + ( 3 K m - - G m |£ z ( t ) - 3 K „ J a m ( T ) dT = 0,

3        3 J                 R 3        3 J*

tT

G g J M ( t , t ' ) ( ? 1 ( t ' ) dt ' - 3 K g J a g ( T ) dT =

T

= I 6 K m - - G m I C 2 - 2 G m - 2 +I 3 K m - - G m |_£ z - 3 K m J a m ( T ) dT ,

3        3 J           R0 3       3 J

(   2 G„            2 G',,^,.T

2 1 3 K g - —g I C1 ( t ) + 9 K g £ z ( t ) + — g J M ( t , t ') C1 ( t ') dt ' - 3 K g J a g ( T ) dT +

2 _ V        2

3 G g + ⁶ K g I C 1 + ⁶ K g £ z - 3

+

I(

- 1 | 2 I 3 K m

J 3

— G„ I C, ( t ) + I 3 K„ + - G„ Ie. m 2           m      m

T I

( t ) - 3 K m Ja m ( T ) dT

T 0                  J

= 0.

Уравнения системы (20) 1 и (20) 2 , линейная комбинация (20) 3 (20) 4 образуют, в свою очередь, систему линейных алгебраических уравнений, разрешая которые относительно C ₂ ( t ) , C ₃ ( t ) и £ _z ( t ) , выражая через

C ˆ₁

и затем подставляя в уравнение (20)4, получаем интегральное уравнение Вольтерры 2-го рода, содержащее только C1 :

( 3 , ( t ) = А ( t ) + y J m ( t , t ' ) ( 2 , ( t ' ) dt' .

Здесь выражения для у и A ( t ) не приводятся вследствие их громоздкости и очевидности получения.

Резольвентой данного интегрального уравнения служит ряд да

R ( t , t ', yX^yX +i ( t , t ‘ ) , i = 0

который сходится абсолютно и равномерно, так как ядро интегрального уравнения (2) — M ( t , t ') , непрерывно при 0 <  t <  t max и 0 <  t ' <  t , и решение уравнения (21) примет вид:

C i ⁽ t ) = g ⁽ t ) + y JX ( t , t ‘ , y ) g ⁽ t ' ) ^dt' .

Г ( t - 1 ') K I ⁶

Если ядро (2) интегрального уравнения разностное: M ( t - 1 ') = e ^ ⁿ , то при b = 1 и постоянной вязкости n = n r резольвента имеет простой аналитический вид:

- ( t -’) K             - ^) K     ( t - 1 -)fr- K I

R (t, t', Y) = ^Y (tt) e   nr   = eY(t-t')e   n'   = e 1  nrJ, i =0 i !

и тогда c t (t-t,)| YI

C i = C 1 (t ) = g ( t ) + yJ e I ^{n r J} g ( t ') dt' . 0

При описании пластического течения во внешнем цилиндрическом слое уравнением текучести Мизеса (9) и вязкоупругого деформирования с учетом структурных изменений путем введения релаксационного ядра Кольрауша (2) получить аналитическое решение задачи (1)–(13) пока не представляется возможным, даже на основе всех принятых упрощений. Разработан численноаналитический метод решения задачи (1)–(13), его алгоритм оттестирован на аналитическом решении задачи (16)–(22).

4.    Численно-аналитический метод

Особенностью задачи (1)–(13) является ее зависимость от истории нагружения, поэтому при численной реализации все уравнения были переписаны в малых приращениях во времени всех параметров. Рассматривалась кусочно-равномерная по координатам и времени сетка с шагами A r g , A r m , A t и A t ' . Аппроксимация всех определяющих соотношений конечно-разностным методом хорошо описана, например, в работе [28], поэтому выделим только особенности развиваемого авторами в данной работе подхода.

На каждом временном слое k приращение перемещений во внутреннем цилиндре записываются как известные функции координат, в которых следует найти только приращение константы интегрирования: A u^k = A C^k • r . Приращения перемещений во внешнем цилиндре рассматриваются как сеточные функции A u ^kj , подлежащие определению из решения системы, получаемой при конечно-разностной записи уравнения (15). При этом приращение константы A C ^ может быть найдено из решения совместной системы, следующей из конечно-разностного представления уравнений (12) и (15). Учитывая малую величину шага, влияние релаксационных процессов на напряжения предлагается отыскивать в виде разности сумм приращений напряжений на всех предыдущих временных слоях и «релаксационных корректировочных» напряжений на текущем слое.

Для нахождения пластических деформаций предлагается использовать метод дополнительных деформаций, при котором реализуется двухэтапный итерационный метод [29]. На каждом шаге определяются нулевые приращения напряжений и деформаций. Если одновременно с этим не выполняется условие (9), то приращение пластических деформаций считается равным нулю и осуществляется переход на следующий временной слой; если условие (9) выполняется, то возникает пластическая деформации, «корректирующая» напряжения. И тогда запускается итерационная процедура вычисления этой пластической деформации.

Алгоритм вычисления совместных вязкоупругих напряжений в стекле с учетом структурных изменений при переходе через фазу стеклования и упругопластических напряжений в металле на каждом временном слое представлен в Таблице 1.

Таблица 1. Алгоритм реализации

№ шага 0 < r < R0, Arg , j = I,.., J0, rj = jArg RI < r < R2 , Arm , j = I,.., J0 , rj = jArm 1 Задание исходных данных Начальные условия ( k = 0 ) (верхний индекс у переменной означает номер временного слоя) AT0 = 0, Auj= 0, As0^,j = 0, Asp3z,j = 0, AaQ^,j = 0, AaO^cor = 0 2 Вычисление структурного параметра Tfk на каждом временном слое k 2 Tf = T ° +Z k i=i 1 - exP V ^ k ^ k -1 '-2(512^ 2 '11AT, 1         n r         J V                   JJ +у nrAk k i_i nk 1-1 , k „.,.,0             k 1   /^O 1)        k(-ik\ 1   k T-1)

lg n = lg П + B e ( ( ^Tf )  - ( ^T ) ) ⁺ B, ( ( ^T )   - ( T f ) ) ^,

	к       (        2 A Tf a _C e +(C f -C e ) A T T
3	Определение приращений перемещений на каждом временном слое k
	A u k _ A Ckr j	f^ r m + 1 1a u ‘ -f A r m - + 2 2 A u k +f1 - A r m 2 A u k, _ j + I                                    /                                  j - I V 2 ' j    J         V ' j      J        V    2 ' j J K,. 2      ( NePk - 1 NePk - 1    Ac- Pk - 1 AcPk - 1 _     2 Gm A ' m    1 As 'j + I -As 'j - I + As ' , j -AS i I ( 4 G m /3 ) + K m V    2A ' m              ' j       J

( k -I)          k

U j = u j   + A U j

Дополнение системы на шаге № 3 аппроксимированными уравнениями (12) с использованием формулы шага № 5 для нахождения приращений A C k , A u k , As k .

A u k

A C k = — J 0- ,

JoA 'g a '-I + f 3 Gg + 6 Kg \ C + f 3 Kg - 3 Gg jAs k - 3 Kg Aa g -AaLz =

(4        2 Auk,-Auk (     1   Vauk3

= a ^k + 1 - G + 3 K I — J + ¹---- J ⁰- + 1 3 K — G I — J ⁰- + As ^k - 3 K Aa ^k - 2 G As pk ',

'J Q V 3 m m J      a r        V m 3 m J I r       z I mm m oJ 0 ^,

. , 24          2 Auk -Auk , 2       2   2(Auk.2

k - I                                       J 1           J I^-1                                         J I Ar- k                     k               \<-Р^к - I

• ^a rJ i ⁺ (3 ^Gm ^{+ 3} K m J---- A r ----⁺ V ³ K m - 3 G JI R ^{+ AS} ' Г³ m - ^{2 G} ""  ^AS 'J । =

R O" 1 a k ^{- I} + ² 1 3 K g -2 G g Ia C k +I 3 K g + - G g Ias k -3 K g Aa g -AaI = RR 1 £ ( a k - ' - +a jj ) , ² V         V ³ J V ³ J                            J J । J о ² j = j q + i

• .     ., 24           2 ! 2       2 2 2 A uk -A uk, A uk 2         _.. ,

здесь a‘ =a j +I - Gm + 3 Km | Ask +I 3 Km - - Gm I j j' + -j - 3 Km Atam - 2 Gm As j' = 0 j j V 3          J V 3 JV    A rm        rj J

Определение приращений напряжений и напряжений на каждом временном слое k

k

Aa

+

k

z

Aa r = AaJ

ф

g

+ 6 K_g IA C k +

g

² G g К

3 K g

2 _G

g

k

z

k

-3 K g ac k

g

k

³ K g Aa;

—

k

k

g

Aa

k

Aa;

'cor , r , ф ^,

³ K g + ² G

g

k

As'

z

rj

T G m + 3 K m

A u¹

k

A u¹

2A r m

k

-3 K m Aci;

m

2 G m As j ,

k

Aa,

Aa

k

k

cor , z ,

ф j

T G m + 3 K m

k

j

- j - i

3 K m

Aa

k

cor , s

I Aa k

I Aa k

+ I 3 K m

2 _G

m

2 _G

m

A u

k

A u

2A r m

k

j - 1

+ As ^k

z

5 = ' , ф, Z

k

-3 K m A

Aa

k

zj

m

2 G m As j ,

T G m + 3 K m

3 K m

2 _G

m

k

-3 Km A&.\

m

2 G m As j ,

Aa m =a m -A T ,

^a m

A u

= ^a m

k

A u

2A r m

( T k ) .

k

j - 1

k

A u + — j

r j

Ak=a\-AT , a;

g

= ^a g

( ^T )

k

a,

rj

. k -I

= ^a rj

^{+ Aa} k ,

k

a ,

. k -I

=a ,

+ ^Aa Ф , ,

k

^a Zj

. k -I

= ^a zj

k

+ Aa.

zj

Вычисление приращений пластической деформации методом дополнительных деформаций. Если напряжения на k -м шаге по времени удовлетворяют условиям (9), включается счетчик итераций l

		l = 0, к = 0
	На каждой итерации уточняются A C k , As k и определяются Ao k , Ao p и Ao k	k   00       k   00 0_ 3      rj 3(     p j        zj )                  3      p j 3( rj        zj ) r j               2 Gm            ’         j               2 Gm            ’ — Ao k. --(Ao0. + Ao0) As”. = 3 zj 3 (     ' j . zj              2 G m Расчет интенсивности приращений пластических деформаций Asl ipj = ^y \'(As ” -As P i ) + (As P i As 0, ) + (As P -As P ) - Переопределение приращений пластических деформаций как Де p 0=Л С f 2 Дст0 _ 1 / Дст0+ Дст0 \) rj      2o T  13    4   3(     p j        zj ) J as p 0 = 3ЛГf2Дст0 _!(Дст0+ Дст0)), p j     2o T  (3     ’ j   3(     rj       zj ) J p 0 As p = —6 i L-f2 Aa ” - 1 Aa” +Aa “ I. zj      2o T 13 zj 3V ” '        rj ’) Переопределение интенсивности приращений пластических деформаций As Pi = 3y V( As P ° - As i ) 2 + ( As i -AS zP “ ) 2 + ( As p” -As Pi” ) 2
		Найденные приращения пластических деформаций As P 0, As; pj 0, As Pj 0 подставляются в уравнения шагов № 3 и 4 и находятся приращения перемещений. Затем по формулам шага № 5 переопределяются напряжения. Далее осуществляется итерационный процесс вычисления приращений деформаций l = 1 д P 1 =3_KL f2Д k 1 _ 1/д 1+ д 1 rj      2o T (3      rj 3(     p j         zj)) , д P 1=3As ip lf2ДО1 Л/До1 +ДО1 p j 2o T 13      p j 3(     rj       zj)) p 0 As P = —j f 2 Ao1 - 1 Ao' +AH1 I, zj 2o T 13 zj 3V ” j        rj ’) As P'= y- V( As P ' - As p ; ) 2 + ( As p1 - As P 1 ) 2 + ( As P1 - As Pj ) 2 l = 2 Итерационный процесс прекращается при выполнении условия u l - u1"' / u l -s• Здесь s - заданная точность. Тогда l = k , и происходит переход на следующий - ( к +1 )-й, временной слой

Таблица 2. Параметры отжига

№ режима	1	2	3	4	5	6	7	8	9
q 1 ,°С/с	0,008	0,016	0,05	0,008	0,016	0,05	0,008	0,016	0,05
t 2 , с	1800	1800	1800	3000	3000	3000	0	0	0

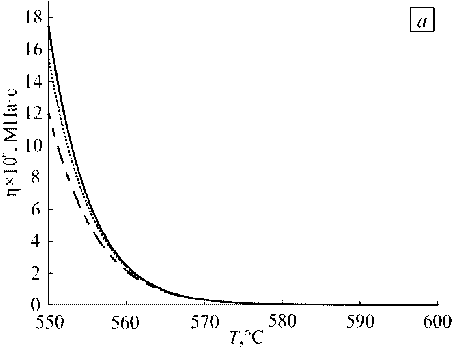
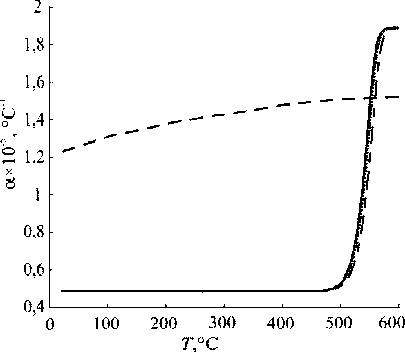
Расчеты показали, что в начале охлаждения структурная температура совпадает с текущей температурой, а далее начинает отставать и стабилизируется (становится постоянной) (Рис. 5). С отставанием этой температуры отражается на структуре жидкости: она перестает успевать за поведением структурной (фиктивной) температуры. Стабилизация последней показывает, что стекло находится в замороженном состоянии. На рисунке 6 представлены результаты изменения вязкости и коэффициента линейного температурного расширения для моделируемых режимов 1, 2 и 3 отжига в стекле и металле. Изменение коэффициента незначительно и почти линейно зависит от температуры.

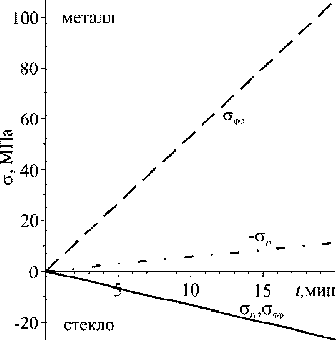
По кривым интенсивности напряжений (Рис. 7 а ) и напряжений σ _r и σ _z (Рис. 7 в , г ) в стеклянном компоненте спая при отжиге до T _от = 400 °С, что соответствует T_f =const с разными скоростями охлаждения, можно сказать, что при такой температуре отжига изменение скорости после выдержки не сильно повлияло на результаты расчета. Однако заметна разница в максимальных значениях напряжений (в 1,5 раза (Рис. 7 в , г )) на первом этапе охлаждения для разных режимов. Поскольку напряжения имеют положительный знак и являются растягивающими, то предпочтительно выбирать скорость охлаждения с меньшими растягивающими напряжениями.

б

Режим h 4, 7

Режим 2, 5. 8

Режим 3. 6, 9

Рис. 6. Изменение вязкости ( а ) и коэффициента линейного температурного расширения стекла ( б ); для сравнения на ( б ) пунктиром показана зависимость от температуры коэффициента металла

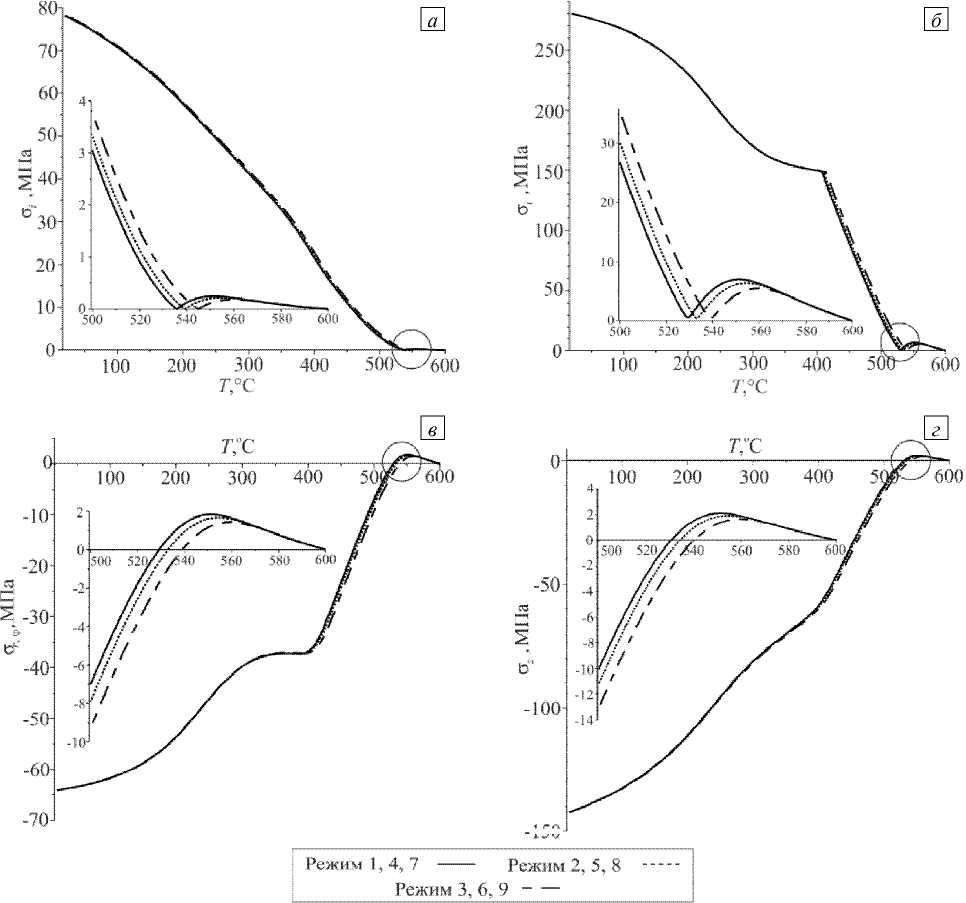
Рис. 7. Распределение интенсивности напряжений σ _i в стекле ( а ) и металле ( б ), а также распределение напряжений, возникающих

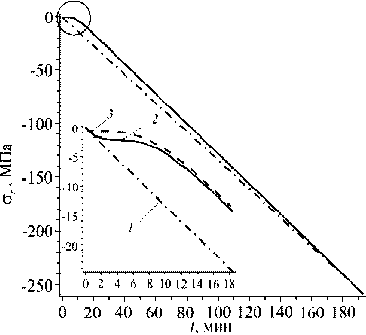
Рис. 4. К сравнению результатов расчетов с аналитическим решением (зависимость 1 ); данные вычислений по

а

б

алгоритму из таблицы 1 при различных шагах по времени, решения ( а ) и характер напряжений ( б )

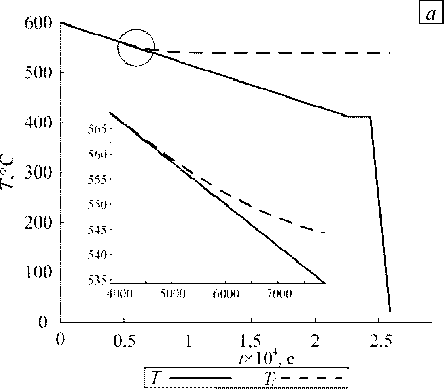
Δ t : 0,01 ( 2 ), 0,1 ( 3 ); демонстрация сходимости численного

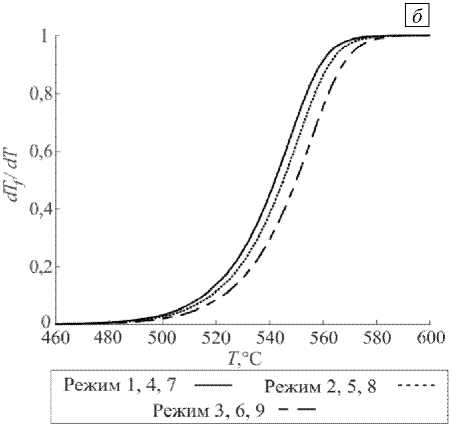
Рис. 5. Пример изменения фиктивной температуры для режима № 1 ( а ) (в выделенной области приведен интервал температур, в котором происходит отклонение T _f от T ); изменение скорости фиктивной температуры для трех режимов отжига ( б )

в сечении стеклянной составляющей стержня σ _r ( в ) и σ _z ( г ), для разных режимов отжига

Отдельная задача — подбор температуры отжига. На рисунке 7 приведены результаты для Т от. = T f = const с нулевой погрешностью отклонения от константы (для рассматриваемых теплофизических параметров Т _от = T f = 400 ° С (Рис.5)). Изменение интенсивности напряжений в стекле при разных температурах отжига (Рис. 8), позволяет отметить незначительный скачок (см. выделенный фрагмент) в значении интенсивности при 540°С. Данная температура выбиралась далее в качестве T _от при расчетах по режимам из Таблицы 2. Температуры отжига на рисунке 8 соответствуют различным значениям фиктивной температуры: 570°С отвечает T f = T ; 540°С — T f ^ T и T f = const; 493°С — T f ^ T и T f = const с погрешностью отклонения от константы е = 0,005 .

Поскольку для стекла опасными являются напряжения растяжения, то в качестве оптимального в данном случае был выбран режим № 4 (Табл.2), при котором напряжения растяжения на первом этапе достигают минимальной величины и максимально уменьшаются при выдержке, включающей охлаждение со скоростью 0,008ºС/с до температуры 540ºС, выдержку в течение 3000 с, дальнейшее охлаждение со скоростью 0,25ºС/с.

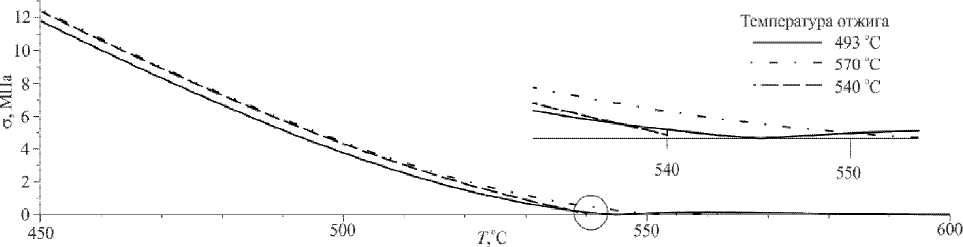
Рис. 8. Распределение интенсивности напряжений в стекле при разных значениях температуры отжига T _от

6.    Заключение

Поставлена и решена задача определения изменения параметров напряженно-деформируемого состояния в двухслойном цилиндрическом стеклометаллокомпозите при отжиге с учетом процесса стеклования во внутреннем стеклянном слое и пластического деформирования внешнего металлического слоя. Для метода ТНММ предложен алгоритм расчета цилиндрического стеклующегося слоя, сопряженного с пластично деформируемым нестеклующимся слоем. Для конкретно выбранных материалов продемонстрирован расчет технологических напряжений по разработанному алгоритму и выбран оптимальный режим отжига.

Расчеты по предложенному алгоритму позволяют вычислить технологические напряжения, возникающие вследствие структурных и механических релаксационных процессов. В целом алгоритм может быть применен для моделирования термонапряженного состояния в многослойных цилиндрических композитах, имеющих стеклующиеся слои.

Исследование выполнено при финансовой поддержке гранта Министерства науки и высшего образования РФ №14.584.21.0034. Уникальный идентификатор соглашения RFMEFI58418X0034.