Метод расчета нестационарного обтекания произвольного профиля

В данной работе рассматривается нестационарное безотрывное обтекание плоским потенциальным потоком несжимаемой жидкости профиля, колеблющегося как твердое тело с малой амплитудой по некоторому гармоническому закону. По данной проблеме опубликовано большое число специальных монографий и журнальных статей, но практически все имеющиеся результаты получены для слабоизогнутых и тонких профилей [1-10]. В данной же работе предлагается метод расчета нестационарного обтекания произвольного или телесного профиля, приведенного ранее авторами в работе [11] к интегральным уравнениям Фредгольма второго рода относительно величины стационарной скорости v ₀( 5 ) и амплитудного значения нестационарной части относительной скорости v(s).

1 Устранение особенности ядра

Введем прямоугольную систему координат OXY, так, что ось OX совпадает с геометрической хордой профиля, в среднем положении, причем х=0 соответствует носику, а координата х=1 — хвостику профиля. Обозначим через L_t — контур профиля в момент времени t, через L — контур профиля в среднем положении и, соответственно, C t и С — вихревые следы. Предполагаем, что в бесконечном удалении перед профилем жидкость имеет постоянную скорость V _m .

Рассмотрим полученное ранее авторами [11] интегральное уравнение Фредгольма второго рода относительно величины нестационарной скорости v ( 5 ):

• ^{1    v ( 5} ) ^- 1- J ^{v ( a} ) R ^{( 5} , ^ ) d a = F ⁽ v 0 ^{( 5} ), ⁵ )                      ⁽¹)

• 2       2п *

то

R ( 5 , a ) = K ( 5 , a ) - jq j e - j ^quK ( 5 , u ) du ,

K ( 5 , a ) = - Re i

ie‘ “ ^{( т} )

z ^{( 5} ) ^- ^ ^{( т} )

( x ( 5 ) - Z ( a )) sin a ( 5 ) - ( y ( 5 ) - n ( a )) cos a ( 5 ) ⁽ x ^{( 5} ) ^- £ ⁽ a ⁾⁾² + ⁽ y ^{( 5} ) ^- п ^{( т ))2}

то q2 A1 x j e - jquK (5, u) du

F ^{( v} 0 ^{( 5} ), ⁵ ) = ^Re i ^{ф ( 5} ) + 1-2 n

Ф ( 5 ) = e

,a ( 5 ) ( jq f g^{( a} ) e^{i a ( a} ) ^{d a} I ^{2 n j}     z ^- s

- — f v ₀( a ) g ^{( 5} ) ^- g⁽ a ) d a + 2 n i ^{j 0V}     ( z - s )²

ie - ^{i a ( 5} )

+-----

в ( 5 )

jq ^

где i — мнимая единица, j — мнимая единица, связанная с временными процессами, a (s ) — угол наклона к оси OX касательной к контуру L, a 1 (s , t ) = a (s ) + в ( s ) e^jmt — угол между касательной к контуру L t и осью

ОХ, q = ^- — число Струхаля, ю — круговая частота колебаний, g = gx - igy — комплексная форма гармонических колебаний профиля. Интегрирование по контуру ведется в положительном направлении (против часовой стрелки). Все линейные размеры нормированы к длине хорды профиля b, а величины, имеющие размерность скорости, — к скорости набегающего потока V„ .

Особенностью уравнения (1) является то, что его ядро и правая часть конкретно выписываются лишь при известном решении соответствующей стационарной задачи. Это связано с определением вихревого следа C t за профилем, который приближенно совпадает с критической линией тока стационарного потока С . Поэтому в дальнейшем будем предполагать, что нам известны все характеристики стационарного потока.

В этих формулах контур профиля L представляет собой кривую, гладкую в смысле Ляпунова всюду, за исключением задней кромки В, которая является точкой возврата. Выбор контура L с точкой возврата в задней кромке определен требованием однозначности направления скорости в этой точке, что необходимо для построения линии вихревого следа за профилем. Выражение ядра R(s,o) отличается от ядра K(s,o) для соответствующей стационарной задачи наличием членов, содержащих несобственный интеграл по линии вихревого следа, который моделируется линией разрыва касательных скоростей, расположенной вдоль критической линии тока стационарного потока. Этот интеграл сходится и для практических расчетов можно перейти к конечному промежутку интегрирования.

Интегральное уравнение (1) с данным ядром справедливо для всех точек контура L за исключением задней кромки В, в которой s=a=о и ядро имеет полюс первого порядка. Для однозначного определения решения уравнения (1) используется известный постулат Кутта — Жуковского, который формулируется так: скачок касательной составляющей скорости жидкости в задней кромке равен интенсивности сходящего с нее вихря:

v ( + 0) + v ( - 0) = —jq— [v ( s ) ds + —— A, , (2) v o (O) 1 v o (O) ¹ '

где v ₀(0) — скорость стационарного потока в точке В, у(+о) и у(-о) — предельные значения относительной скорости жидкости при подходе к точке В снизу и сверху, соответственно.

Условие (2) используется для устранения особенности ядра уравнения (1) в задней кромке. Из (1) следует, что:

v ( ± 0) = Y J v ( ст ) R ( ± 0, ст ) d ст + 2 F ( ± 0).

Тогда уравнение (1) с учетом (2) и (3) запишется в виде:

^{1 v ( 5} ) ^-     J v ^{( ст} ) R ^{( 5} , ^ст )

^{2       2 п} L    I

-

1       z         \

- R ( + 0, ст ) + R ( - 0, ст ) +

jq ⁿ v 0 (0)

dст =

= F ( 5 ) - 2 F ( + 0) + F ( - 0)

-

A, | .

2 v 0 (0) ¹ )

Ядро полученного уравнения (4) не имеет особенностей на контуре L, и его решение совпадает с решением (1).

Гидродинамический смысл проведенного устранения особенности ядра состоит в том, что решение уравнения (1) ищется в классе функций, обеспечивающих непрерывность давления всюду в потоке, в том числе и в острой задней кромке.

2 Метод расчета

Интегральное уравнение (4) разделим на действительную и мнимую по j части. Для этого запишем его в операторном виде:

^{( A +} j"^B ) v ^{( 5} ) = a ⁺ jb , ^{v ( 5} ) = ^v 1 ^{( 5} ) + jv 2 ^{( 5} ),                    ⁽⁵⁾

где

A = E - 1 ff K ( 5 , ст ) - K ^{( +} °' ^ст ) ⁺ K ( ' ^ ⁾ - n L ^                   2

Г "  ■ f^Z А K ^{( + 0,} u ) ⁺ K ^{( - 0,} u ) Y? Y?

- q J sin qu I K ( 5 , u )------------- I du I d ст ,

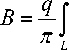
ю f

J cos qu I K ( 5 , u )

K ( + 0, u ) + K ( - 0, u )

du

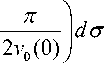
a = 2 Re i

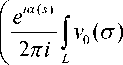
g ^{( 5} ) - g ст ) d ст ⁽ z ^- s )

q ² A "r

----¹ [cos( qu ) K ( 5 , u ) du -

^{2 п} 0

b = q Re i

e

1 г g ( ст ) e ^{a ( ст} ) d o _v ^{n i j}      z ^- q

-

qg ⁽ s ) +

+ q A j _sln( qu ) K ( s , u ) du - *±»± » < - 0). П "                           2

Критическая линия тока стационарного потока, необходимая для вычисления несобственных интегралов в формулах (6)-(9), определяется как решение следующей задачи Коши:

' dx , .

= v 0 x ⁽ x , y >.

dy

Tl ⁼ v 0 •⁽ x , y ),

x ⁽⁰⁾ = x B = 1 у ⁽⁰⁾ = У в = 0.

Здесь (xB, yB) — координата выходной кромки профиля в среднем положении. Функции v0x (x, у), v0y (x,у) определяются по формуле:

v 0 x

iv ,, = J-f ^v 0 ^{( ст} ) ^dCT ± e-• ^{2 n} i L z ^{( t} ) - ^{z ( ct} )

(ii)

где z(t) - САст) = (x(т) - ^(ст)) + i(у(т) - п(ст)), т — длина дуги контура, отсчитываемая вдоль линии вихревого следа от задней кромки, 6 — геометрический угол атаки, образуемый вектором скорости потока на бесконечности V„ и осью OX.

Разделяя уравнение (5) на действительную и мнимую части, получим систему двух уравнений:

Av , ( s ) - Bv ₂ ( s ) = a ,

Bv₁ ( s ) + Av ₂ ( s ) = b .

Из первого уравнения находим:

v,( s) = A-1 Bv 2( s) + A-1 a.(13)

Подставляя (13) во второе уравнение (12) и решая полученное уравнение относительно v ₂( s ), имеем:

v2(s) = (BA-1 B + A)(b - BA-1 a).(14)

Откуда, подставляя в (13), v1 (s) = A-1 B(BA-1 B + A)(b - BA-1 a) + A-1 a.(15)

Далее заменой интегралов в уравнениях (6)-(9), (11) конечными суммами методом, предложенным в работах [12-14], получим системы из N алгебраических уравнений относительно искомых величин, которые можно решить с применением ЭВМ.

Заключение

Интегральное уравнение Фредгольма второго рода относительно величины нестационарной скорости v ( s ) справедливо для всех точек контура L за исключением задней кромки В, в которой s=σ=о и ядро имеет полюс первого порядка. Для устранения особенности ядра уравнения используется постулат Кутта — Жуковского. Гидродинамический смысл проведенного устранения особенности ядра состоит в том, что решение ищется в классе функций, обеспечивающих непрерывность давления всюду в потоке, в том числе и в острой задней кромке. Критическая линия тока стационарного потока, необходимая для вычисления несобственных интегралов, определяется как решение задачи Коши (10). Заменяя интегралы в уравнениях (6)–(9), (11) конечными суммами, получаем системы из N алгебраических уравнений относительно искомых величин, которые предполагается в дальнейшем решить с применением ЭВМ.