Метод расчета параметров пересечения нулевого уровня для центрированных стационарных процессов

Предложен метод приближенного расчета параметров выбросов центрированных случайных процессов за нулевой уровень. В основу расчета положено использование корреляционной функции R1 (т) импульсной случайной последовательности B1(t), полученной в результате идеального двустороннего ограничения на нулевом уровне (клиппирования) исходного центрированного слу- чайного процесса X (t). Рассматривая импульсную последовательность B1(t) в качестве порождающей, можно получить из нее ряд импульсных последовательностей Bi (t), i = 2; 3 ... k путем деления B1(t) по частоте в i раз. В итоге, помимо исходной корреляционной функции R1 (т), появляются еще (к - 1) функций Ri (т), несущих дополнительную информацию об интервалах между сменами знака исходного центрированного случайного процесса X (t) •

Получена формула для приближенного расчета функции p ₀ ( т ) , которая является вероятностью того, что за время Т , отсчитанное от произвольного момента t ₀, не состоялось ни одного пересечения процессом X ( t ) нулевого уровня. Располагая функцией р ₀ ( т ) , легко рассчитать искомую плотность W ( т ) распределения интервалов между смежными нулями процесса X ( t ) . Погрешность приближения зависит от числа k учтенных функций R i ( т ) и может быть сделана сколь угодно малой с ростом k .

На примере моделирования трех широкополосных гауссовых процессов показано, что при k = 8 относительная погрешность расчета W ( т ) не превышает 5% даже при снижении величины относительно максимальных значений в 20 раз в области экспоненциальных «хвостов» плотности.

Постановка задачи

Многие задачи обнаружения и различения случайных и детерминированных сигналов на фоне помех с априорно неизвестными статистическими характеристиками могут успешно решаться с помощью устройств, адаптирующихся к наиболее информативным параметрам выбросов принимаемого колебания.

К таким параметрам относятся, например, среднее число пересечений одного или нескольких относительных уровней анализа за фиксированное время, распределение длительностей выбросов за уровень и пауз между ними, распределение времени пребывания сигнала в заданных границах. Полезной может оказаться информация о законераспределения интервала времени между произвольным моментом и первым пересечением сигналом нулевого уровня, о среднем интервале между экстремумами сигнала и т.д.

Примерами могут служить задачи различения вида сигнала (речевой, музыкальный, гармонический, импульсный), обнаружения сигнала известной формы в шумах, обнаружения и коррекции «щелчков» при цифровой передаче речи и музыки методом ИКМ, измерения частоты гармонических сигналов на фоне помех и множество других.

Несмотря на длительный интерес ряда исследователей и большое прикладное значение, разработка теории выбросов случайных процессов далека от своего завершения. Это объясняется сложностью математического описания тонкой структуры случайных процессов. Самыми изученными параметрами выбросов являются их средние длительности за уровень и, отчас- ти, дисперсии длительностей, а также начальные участки (первые приближения) плотностей распределения длительностей выбросов. Ввиду сложности строгого решения ряда задач в области теории выбросов, полезными оказываются приближенные результаты, которые удается довести до инженерных приложений.

Одновременно, в последние десятилетия для исследования характеристик выбросов широко используются методы статистического моделирования случайных процессов на ПК.

В предлагаемой статье кратко описан приближенный метод расчета закона распределения интервала времени между произвольным моментом и первым пересечением случайным процессом нулевого уровня с любым знаком производной (либо сверху вниз, либо наоборот). Полученные результаты позволили получить также оценку плотности распределения интервалов между нулями нескольких широкополосных гауссовых случайных процессов. Моделирование этих процессов на ПК позволило оценить качество приближений.

Показано, что ценой усложнения расчетов по предложенному методу можно получить сколь угодно малую погрешность приближений. Дополнительным достоинством данного метода является его применимость для центрированных случайных процессов с произвольным законом распределения мгновенных значений и произвольной автокорреляционной функцией.

Описание методикирасчетапараметров пересечения нулевого уровня

Для расчета параметров пересечения центрированным стационарным случайным процессом X ( t ) нулевого уровня можно использовать функции корреляции Rk ( т ) клиппированных после -довательностей B_k ( t ).

На рис. 1 представлена реализация случайного процесса X ( t ) и семейство клиппированных импульсных последовательностей B_k ( t ) при k

При k = 1 последовательность B₁ ( t ) представляет собой двуполярный импульсный процесс на выходе идеального ограничителя с характеристикой f ( x ) = 1, x > 0 , f ( x ) = -1, x < 0 при подаче на его вход случайного процесса X ( t ). Последовательности B_k ( t ) при k = 2; 3 ... формируются из порождающей их последовательности B₁ ( t ) путем ее деления по частоте в k раз (или суммирования k смежных интервалов между соседними сменами знака).

-10

Реализация случайного процесса X t)

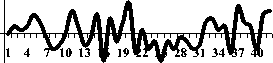
t

Нетрудно показать, что функции корреляции R k ( т ) клиппированных последовательностей B_k ( t ) можно выразить через P_k – вероятности k нулей с любым знаком производной на интервале т, отсчитанном от произвольного момента времени. Опуская преобразования, запишем в общем виде:

Клиппированная последовательность B1(t)

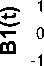
-2

Клиппированная последовательность B2(t)

, , "    22(0)т"

Rk ⁽ т ) = [ 1 - *] ⁺

⁺ k [ Pk + 1 ⁺ 2 Pk + 2 ⁺ 3 Pk + 3 ⁺ - ^{+ ( k} - 1 ) P 2 k - 1 ] ⁺ + 4 [ P 2 k ⁺ P 2 k + 1 ⁺ P 2 k + 2 ⁺ •" ⁺ P 3 k ] ⁺

• ⁺ 4 [ ⁽ k ^{+ 1 )} P 3 k + 1 ^{+ (} k ^{+ 2 )} P 3 k + 2 ⁺ “( 2 k ^{- 1 )} P 4 k - 1 ] ⁺

• ^{+8 ⎡}⎣ ^P4k^+P4k+1^+P4k+2^+...+P5k ^⎤⎦ ^{+          (1)}

• ⁺ k [ ^{( 2к +} 1 ) P5k + 1 ⁺ - ^{+ ( 3k -} 1 ) P6k - 1 ] ⁺

• ^{+ 12} [ P6k ⁺ P6k + 1 ⁺ P6k + 2 ⁺ ... ⁺ P 7 k ] ⁺ ...

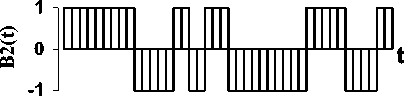
Клиппированная последовательность B3(t)

где 2 ( 0 ) - среднее число (интенсивность) нулей случайного процесса X ( t ) в единицу времени. Подстановка в (1) значения k = 1 дает

R 1 ( т ) = [ 1" 2 ^ ( 0 ) т ] + 4 ( P ₂ + P 3 ) + 8 ( P 4 + P 5 ) +

+ 12 P+P+ 16 P+P+ ... 67    89

С учетом очевидных соотношений:

-1

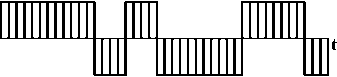
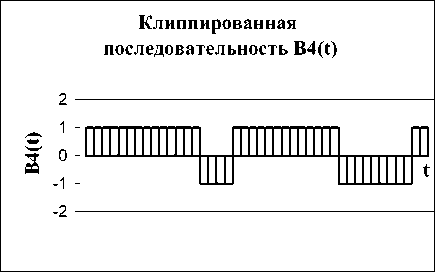
Рис. 1. Клиппированные последовательности B_k ( t ), k = 1; 2; 3 и 4

да            да

L Pk = 1, 2 ^k • Pk = А ( О ) т ,         (2)

к — О         k — 1

можно выразить искомую функцию через функции корреляции из (1).

Функция Ро ( т ) является вероятностью того, что за время т , отсчитанное от произвольного момента, не состоялось ни одного пересечения нулевого уровня. Изменяя в формуле (1) значения параметра k в диапазоне k = 1 … 8 и используя уравнения (2), получим

R1 ( т ) R₂ ( т ) 3 R ( т )

P 0 ^{( т} ) = ^{Л ( 0 ) т +}-14-⁺-22--- ³— ⁺

+2 R ( т ) -5 R 5< ^{T )} -3 R 612-7^7< ^{т )} +   (3)

+ 8 R 8 ⁽ т ) - 2 - P 11 - 3 P 12 - ⁷ P 13 - ^12P 14 - 18 P 15 - -

Как следует из выражения (3), оно представляет собой оценку сверху истиной функции P0 ( т ) . До тех значений интервала τ , при которых можно пренебречь вероятностями появления одиннадцати и более нулей, оценка P0 ( т ) должна оставаться хорошей. Можно показать, что увеличение k max вдвое (с k _max = 8 до k _max = 16) снижает погрешность (3) с P 11 до P 21 . Однако в этом нет необходимости, поскольку с удлинением ряда (3) и ростом интервала τ неизбежен рост погрешности вычислений Rk ( т ) и, как следствие, функции Р о ( т ) .

Формула (1) получилась довольно громоздкой и использовалась совместно с (2) исключительно для вывода (3). Вычисление интенсивности 2 ( 0 ) смен знака случайного процесса X ( t ) и функций корреляции Rk ( т ) клиппированных последовательностей B_k ( t ) в (3) целесообразно производить на ЭВМ во временной области, используя готовое программное обеспечение.

Для расчета плотности W (т ) распределения интервалов τ между смежными пересечениями нулевого уровня случайным процессом X ( t ) воспользуемся результатами [ 1 ] :

Оценка снизу (6) является более грубой сравнительно с оценкой сверху (5). Из [3] следует

W (т )

2 1d

+ —— *—й ^ ( ⁰ ) dT

1       я 2

1      d

W ^{( т} ) = 1 ( 5 ) * 1? P ^{( т ) .}

Дважды дифференцируя по τ , из (3) имеем

1 ,R1" (т)

∗

2 ( 0 )      4

£1 ^k * ^{( p} 2k + 1 ^{+ p} 2k + 2 )

Как видно из (7), погрешность в (6) определяется суммой вторых производных вероятностей появления трех и более нулей случайного процесса X ( t ) на интервале τ . Эта погрешность нарастает значительно быстрее, чем в (5). Следовательно, в широком диапазоне значений τ плотность W (т ) должна практически совпадать с оценкой сверху из (5).

Для проверки этого утверждения удобно использовать известные выражения р_к ( т ) , соответствующие закону Пуассона:

[^{2 ( 0 )} * ^т ] ^{k p} k ^{( т} ) = -(k)T"

* exp [ - 2 ( 0 ) * т ] ,

где 2 ( 0 ) = —-- интенсивность смены знака пу-

2 τ ₀

ассоновского процесса.

Средний интервал между соседними сменами знака т = ——— = 2т „. При k = 0

,       . ^я( 0 )       0

W (т) = , Л ^{V 7} 2( 0 )

R1 (т) R2 ( т ) 3R3 ( т V

--1-----+

''                             ''                             ''

5R τ 3R τ    7R τ

+ 2R. (т )----⁶⁽^-- 72-2 + ⁽⁵⁾

+ 8R8 ^{( т ) ]} - 2 ( 0 ) * { Р^{1 ( т} ) ^{+ 3} Р^ ^{( т} ) ⁺ ”^}’

Как видно из выражения (5) в квадратных скобках, оно представляет собой оценку сверху истиной плотности W (т ). До тех значений интервала τ , при которых можно пренебречь вторыми производными вероятностей появления одиннадцати и более нулей, оценка W ( т ) должна оставаться хорошей.

Интересно отметить, что первое слагаемое в (5) представляет собой оценку снизу плотности W (т ). Как показано в [2-3]:

W (т) > -1- * R1 (Т) .

V 7   2 (0)

p _п ( т ) = exp —— . Из (4) после двойного

0⎜

⎝0⎠ дифференцирования р0 (т) имеем

W ( т ) =--- exp

2 τ ₀

τ

2 τ

Нетрудно рассчитать абсолютную погрешность оценки (5):

А (т) = 1(0) *{Р11 (т) + 3Р^ (т) + "} и сравнить ее с истинным значением плотности из формулы (8) при различных значениях интервала т . Расчеты показали, что при т < 6тQ = 3т относительная погрешность оценки сверху по формуле (5) не превышает 5%. При τ=6τ0 =3τ значение W(т) в (8) снижается в 20 раз относительно максимальной величины (при τ = 0). Следовательно, оценка сверху по формуле (5) справедлива даже в области «хвостов» плотности W (т).

Отметим, что для реальных широкополосных процессов относительная погрешность оценки (5) может дополнительно снизиться. Из-за статистической связи длин соседних интервалов, вероятность появления нескольких коротких интервалов подряд для реальных процессов может уменьшиться. Это вызовет, сравнительно с пуассоновским процессом, снижение вероятностей большого числа смен знака на интервале τ , при неизменной интенсивности X ( 0 ) .

π 6

G, ( to ) =---- т 0 = const ,0 <  to <--- (9)

¹6    ⁰                      τ ₀

Гауссова СПМ имеет вид:

-

2 2 Л ω τ ₀ ⎞_⎟

4 ⎟

. τ ₀ . (10)

Процесс, являющийся первой производной предшествующего, имеет СПМ вида:

Экспериментальная проверка методов расчета плотности

Проведено моделирование на ЭВМ трех широкополосных гауссовых случайных процессов с резко различными энергетическими спектрами. Исследовались следующие процессы:

33 π

G3 ( to ) = —-— . to . exp

-

1 2_2 А

3 ωτ ₀

4 ⎟

. τ ₀ . (11)

-

процесс с равномерным энергетическим

спектром;

-

процесс с гауссовым энергетическим спект-

ром;

- процесс, полученный в результате однократного дифференцирования процесса с гауссовым энергетическим спектром.

Для объективного сравнения между собой все указанные процессы характеризовались одинаковой интенсивностью смены знака X ( 0 ) .

Объем выборки статистических данных для каждого из процессов составил N = 3 *10 отсчетов сигнала, взятых через интервал времени At = 0,1т0. Здесь т0 - интервал корреляции каждого процесса.

Средний интервал между нулями для всех процессов выбран одинаковым и равным 1π т =     =—р*т0 % 2,221т0. Таким образом,

Отметим, что нули первой производной соответствуют экстремумам исходного процесса с гауссовой СПМ. Известно [2], что интенсивность экстремумов гауссова процесса с гауссовой СПМ в 3 раз превышает интенсивность смены знака X ( 0 ) исходного процесса. Для объективного сравнения между собой всех трех процессов,СПМ (11) была нормирована таким образом, чтобы

средний квадрат частоты спектра ω ₁

ω интенсивность смены знака X ( 0 ) = —-π

2и

^τ 0

πτ ₀

были во всех случаях одинаковыми.

Первые два процесса являются результатом прохождения белого шума соответственно через идеальный и гауссов фильтры нижних частот. Третий из процессов сформировался на выходе полосового фильтра, АЧХ которого напоминает АЧХ одиночного колебательного контура низкой добротности.

среднийинтервал между смежными пересечениями процессом нулевого уровня содержал порядка 22-х отсчетов сигнала. Вся выборка статистических данных для каждого из процессов составила N 6

L = ^^ 1.35 . 10 интервалов. Этот объем вы-τ борки обеспечил относительную статистическую погрешность измерений плотности W(т) распределения интервалов не более 0,5% в области максимальных значений плотности. Соответственно, при снижении значений плотности в 100 раз в области «хвостов», относительная статистическая погрешность измерений не превышала 5%.

Спектральная плотность мощности (СПМ) процесса с равномерным энергетическим спектром описывается выражением

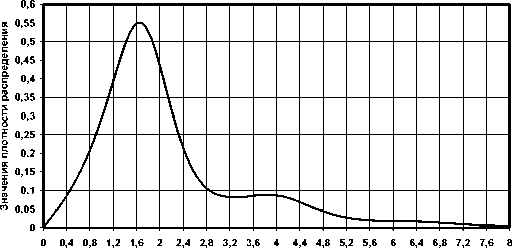
Нормированный интервал между нулями

Рис. 1. Экспериментальная плотность распределения интервалов между нулями гауссова процесса с равномерным энергетическим спектром

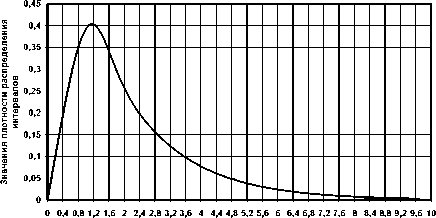
Нормированный интервал между нулями

Рис. 2. Экспериментальная плотность распределения интервалов между нулями гауссова процесса с гауссовым энергетическим спектром

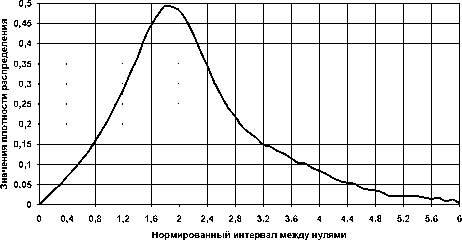
Рис. 6. Расчетная плотность распределения интервалов между нулями производной гауссова процесса с гауссовым энергетическим спектром

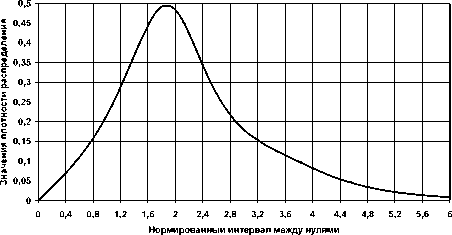
Рис. 3. Экспериментальная плотность распределения интервалов между нулями производной гауссова процесса с гауссовым энергетическим спектром

На рис. 1-3 представлены результаты моделирования на ЭВМ плотности W (т) распределения

интервалов между смежными пересечениями случайным процессом нулевого уровня. На рис. 4-6 показаны результаты расчета по формуле (5)

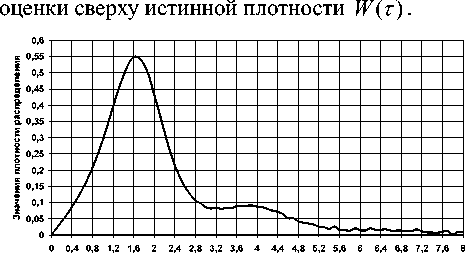
Нормированный интервал между нулями

Рис. 4. Расчетная плотность распределения интервалов между нулями гауссова процесса с равномер-

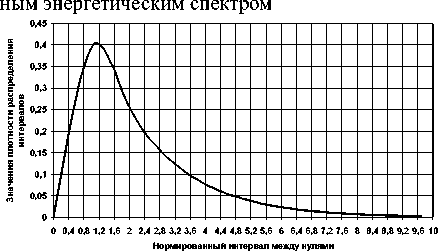
Рис. 5. Расчетная плотность распределения интервалов между нулями гауссова процесса с гауссовым энергетическим спектром

Попарное сравнение одноименных кривых W (т) между собой показывает их практическое совпадение в существенной области значений. Некоторое расхождение (колебательный процесс) наблюдается только в области экспоненциальных «хвостов» плотностей на рис. 4 и рис. 6, где значения W (т ) снижаются в 20 и более раз относительно максимальных величин.

Причиной небольших расхождений в области «хвостов» являются, по-видимому, погрешности расчета вторых производных функций корреляции Rk ( т ) клиппированных последовательностей в формуле (5). Снижение интервала между соседними отсчетами процесса позволит снизить погрешности вычислений первой и второй разностей в (5) до сколь угодно малых величин.

Выводы

• 1.    Показанапринципиальнаявозможностьпри-ближенного расчета, с любой степенью точности, функции P 0 ( т ) распределения интервала времени τ между произвольным моментом и первым пересечением случайным процессом нулевого уровня с любым знаком производной (либо сверху вниз, либо наоборот). При этом не требуется знания закона распределения мгновенных значений центрированного случайного процесса X ( t ) и его функции автокорреляции (либо энергетического спектра). Достаточно располагать семейством клиппированных последовательностей B_k ( t ), полученных из порождающей последовательности B₁ ( t ) путем ее деления по частоте в k раз.

• 2.    Порождающая клиппированная последовательность B₁ ( t ) определяется только своим энергетическим спектром (или функцией автокорреляции), которые связаны с аналогичными энергетическими параметрами исходного случайного процесса X ( t ). Следовательно, вид функции P 0 ( т ) и плотности распределения интервалов W (т ) определяются, главным образом, формой энергетического спектра и мало зависят от закона

• 3.    Результаты моделирования на ЭВМ трех широкополосных гауссовых случайных процессов подтвердили, что при числе использованных при расчетах корреляционных функций клиппи-рованныхпоследовательностей k =8погрешность расчета W (т) остается пренебрежимо малой и сопоставимой со статистической погрешностью измерений в широкой области значений τ , включая экспоненциальные «хвосты» плотности распределения интервалов W (т ) .

распределения мгновенных значений центрированного случайного процесса X ( t ).