Метод расчета предельных нагрузок на сооружения из заполненных цилиндрических оболочек

При проектировании подпорных сооружений, удерживающих грунт от обрушения (в промышленном и гражданском строительстве), возведении эстакад и устоев мостов (в транспортном строительстве), строительстве причальных набережных, пирсов, молов и других объектов гидротехнического строительства находят применение оболочки большого диаметра, занимающие промежуточное положение между защемленными в грунт тонкими стенками и массивными гравитационными сооружениями. Конструкция заполненной оболочки представляет собой тонкую оболочку (выполненную, как правило, из стали или железобетона) с внутренним наполнителем, в качестве которого используется грунт с заданными физическими и прочностными характеристиками. Отношение диаметра D к высоте конструкции H определяет группу оболочек большого диаметра, для которых указанное соотношение D/H находится в диапазоне от 0,7 до 1,0. Оболочки являются сравнительно выгодными экономически и позволяют в значительной мере учесть технологические возможности производителя строительных работ.

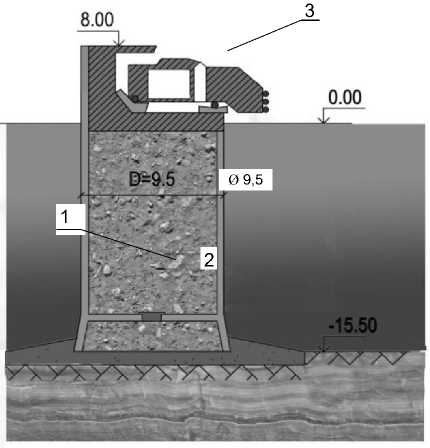
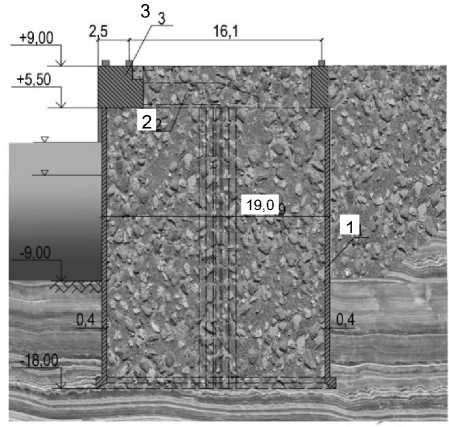
По способу опирания на основание заполненные оболочки можно условно разделить на гравитационные (рис. 1 а), устанавливаемые на специально подготовленный слой прочного несжимаемого грунта («каменная постель»), и частично заглубленные в грунт (рис. 1 б).

а

Рисунок 1 – Схемы вертикальных сечений заполненных цилиндрических оболочек: а – на «каменной постели»; б – заглубленная в грунт основания; 1 – оболочка; 2 – заполнитель (грунт); 3 – элементы верхнего строения (размеры в м)

б

Нагрузки, воспринимаемые оболочками большого диаметра с наполнителем, условно могут быть представлены в виде горизонтальной и вертикальной равнодействующих, из которых первая (для длительно действующих нагрузок), как правило, включается в собственный вес конструкции, а вторая является наиболее критичной, вызывающей потерю устойчивости сооружения.

Основные схемы возможного нарушения устойчивости массивных оболочечных конструкций в результате потери несущей способности оснований могут быть представлены как односторонний выпор грунта основания (рис. 2 а); двусторонний выпор грунта основания (рис. 2 б); сдвиг сооружения по плоскости подошвы (рис. 2 в); глубинный сдвиг и частичный сдвиг с захватом грунтов основания (рис. 2 г, д), а также сдвиг по слабым слоям грунта (рис. 2 е).

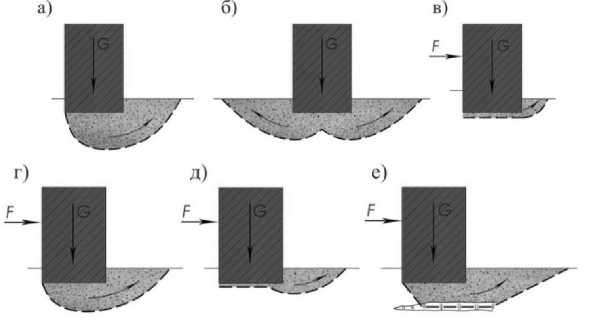
Рисунок 2 – Основные схемы возможных предельных состояний системы «оболочка - основание»

Наибольший расчетный интерес вызывает случай, когда нагрузки, действующие в различных сочетаниях, вызывают внецентренное нагружение оболочки, стремясь вызвать поворот сооружения и его отклонение от вертикали вследствие потери несущей способности основания.

Наблюдаемые случаи отклонения уже возведенных конструкций из оболочек большого диаметра с наполнителем (например, наблюдения за поведением конструкций набережной в г. Риге [2], обследование причальной набережной в торговом порту г. Владивостока) показывают наличие отклонений от вертикали при сохранении целостности конструкции оболочки. Установлено, что оболочки с наполнителем обладают большой «живучестью»: они могут испытывать значительные перемещения без разрушения тела конструкции. Основная причина наблюдаемых отклонений – потеря несущей способности основания, когда в грунте возникают зоны развития полей скольжения и система «оболочка - основание» переходит в область больших деформаций.

Цель исследования – разработка метода определения предельной горизонтальной нагрузки на гравитационные сооружения, выполненные из тонких цилиндрических оболочек большого диаметра, заполненных грунтом.

Существующие методы оценки несущей способности оснований

Расчет оснований выполняют с использованием двух основных расчетных моделей [4]. Первая модель предполагает, что вся область выпора или обрушения или отдельные ее отсеки (рис. 3 а) являются жестким недеформируемым телом. Форма поверхности скольжения в большинстве случаев принимается заданной. На всей поверхности скольжения принимается одновременное наличие состояния предельного равновесия грунта, т.е. по всей границе справедливо условие прочности Кулона-Мора. На этой модели построены основные приближенные инженерные способы оценки устойчивости сооружений, разработанные учеными К. Терцаги, Г. Крейем, Д. Тейлором, Г.Е. Паукером, Н.Н. Масловым, М.Н. Гольдштейном, А. Скемптоном, А. Бишопом и мн. др. Вторая модель оценки устойчивости основания основана на использовании решений теории предельного равновесия (рис. 3 б). Для этой модели принимается, что во всех точках грунтовой среды существует предельное напряженное состояние. При этом во всей толще грунтовой среды возникает система поверхностей скольжения. В рамках этой модели разработаны методы оценки устойчивости грунтовых откосов, представленные в работах Г. Рейснера, А. Како, В.В. Соколовского, С.С. Голушкевича, В.Г. Березанцева, Г. Мейергофа, М.В. Малышева, Ж. Биареза и др.

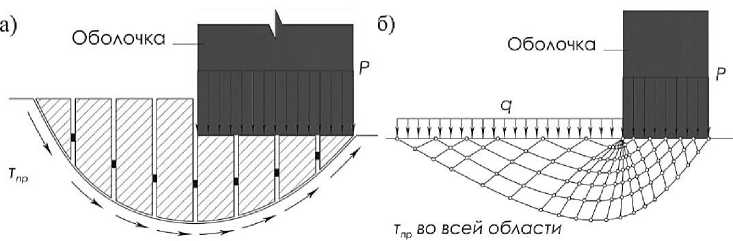
Рисунок 3 – Расчетные модели основания:

а – модель монолитных отсеков обрушения; б – модель теории предельного равновесия

Обе рассмотренные модели, используемые для оценки устойчивости дисперсных сред, сильно различаются по своим физическим предпосылкам. Для инженерного использования наиболее хорошо проработаны методы, опирающиеся на модель твердых отсеков, однако методы теории предельного равновесия являются теоретически более обоснованными и более свободными от допущений в своей постановке [4]. Предлагаемый в работе метод оценки устойчивости цилиндрических оболочек, установленных на сжимаемое грунтовое основание, построен на решении задачи теории предельного равновесия.

Метод расчета предельных нагрузок на сооружения из заполненных цилиндрических оболочек

Далее предлагается теоретическая модель оценки несущей способности основания цилиндрических оболочек, установленных в ряд (как конструкций в составе подпорных сооружений, набережных, пирсов, и др.). На основе положений теории предельного равновесия с дальнейшим использованием простых уравнений статического равновесия определяется максимальная горизонтальная нагрузка (равнодействующая), при которой соблюдается равновесие системы «оболочка – основание» (в основании оболочки не происходит глубинный сдвиг). Для обоснования модели необходимо вначале рассмотреть приложение теории предельного равновесия к решению задачи о несущей способности основания.

Принципы теории предельного равновесия использованы применительно к грунтовой среде для решения задачи определения несущей способности основания под действием нормальной нагрузки. Задача состоит в том, чтобы определить, при какой пригрузке q для заданной на части поверхности основания вертикальной нагрузки p во всех точках грунтового массива наступает предельное напряженное состояние (рис. 4). Как отмечается в различных источниках [8], схема напоминает рычажные весы. Помимо действующих нагрузок, равновесие обеспечивается также силами внутреннего сопротивления грунта, характеризуемые углом внутреннего трения ϕ и давлением связности σ c .

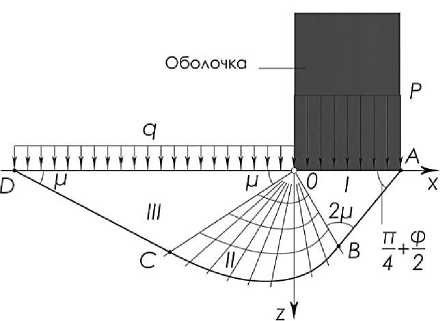
Рисунок 4 – Схема образования полей скольжения

При действии нагрузки в области основания выделяют три зоны [5]. В зоне I грунт под действием приложенной нагрузки p перемещается сверху вниз, в зоне III грунт перемещается снизу вверх (выпирает). Линии скольжения обоих семейств в областях I и III близки к прямолинейным (решение Ренкина для невесомой среды). В переходной зоне II линии скольжения первого семейства – это пучок прямых, а линии второго семейства – окружности или логарифмические спирали (решение Прандтля).

В рассматриваемом случае на грунт основания от сооружения передается, как правило, достаточно большая нагрузка, а поперечные размеры оградительных и подпорных сооружений невелики в сравнении с основными объектами строительства, в результате чего собственный вес грунта в пределах возможной призмы выпора не окажет существенного влияния на распределение напряжений и на очертание кривых скольжения, которые в данном случае определяются в основном внешней нагрузкой. В результате для упрощения решения задачи предельного равновесия при разработке метода оценки устойчивости системы основание принимается невесомым ( γ = 0).

С учетом данного предположения для определения предельной нагрузки p , вызывающей переход грунта в предельное состояние, рассматриваются только граничные условия на бесконечно малых участках вправо и влево от центра равновесия - точки О (р = р о ). Решение задачи [7] позволяет определить искомое давление:

1 + sin ф „. tg _V * e        1

1 — sin ф

1 + sin ф

Р 0 = ^c '          * e

1 — Sin ф

—

с т, . = c * ctg ф *

Рассмотрим ряд цилиндрических оболочек большого диаметра ( n штук), опирающихся на сжимаемое основание и воспринимающих помимо собственного веса G горизонтальную нагрузку F (рис. 5). Заданы основные размеры оболочки: наружный диаметр D , толщина стенки оболочки t , высота конструкции h , плечо равнодействующей нагрузки d , а также физико-механические характеристики грунта основания: угол внутреннего трения ф и удельное сцепление c .

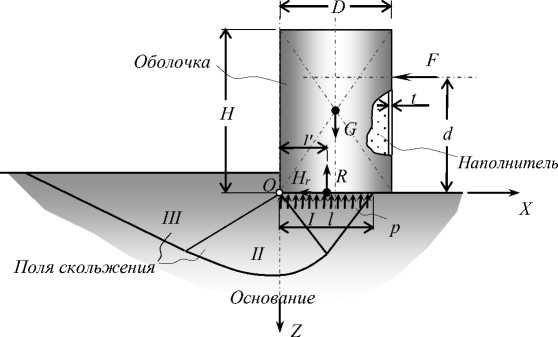
Рисунок 5 - Схема к расчету устойчивости сооружения

Далее разрабатывается зависимость, определяющая максимальную горизонтальную силу F max (при заданной высоте ее приложения d относительно подошвы сооружения), ведущую к опрокидыванию сооружения, которая представляет собой функцию от нескольких переменных, среди которых - размеры сооружения и характеристики грунта основания. Расчет устойчивости проводится по методике единого коэффициента запаса:

M >  k * M₂ , (2) где M 2 - опрокидывающий момент, определяемый действием горизонтальной равнодействующей нагрузки F и плечом d как расстоянием от подошвы сооружения до уровня приложения горизонтальной равнодействующей F ; k - коэффициент запаса, назначаемый в зависимости от класса сооружения и принимаемый равным по разным источникам 1,2^1,4 [3]; M i - удерживающий (восстанавливающий) момент, возникающий в результате действия сил собственного веса сооружения.

Устойчивость сооружения обеспечена в случае, если восстанавливающий момент превосходит предельный. Равенство указанных моментов определяет максимальную горизонтальную нагрузку F max , превышение которой ведет к опрокидыванию сооружения. При достижении предельной нагрузки сооружение полностью теряет проектное положение, так как центр тяжести системы переходит за точку приложения равнодействующей предельного давления.

Для определения предельной нагрузки F max , воспринимаемой оболочкой, рассматривается работа грунтового основания сооружения в пластической стадии. При достижении предельного давления в грунте развиваются поверхности скольжения, условно объединенные в поля (области) скольжения (см. рис. 4, 5). Предельная нагрузка при этом определяется по формуле (1). Собственный вес цилиндрической оболочки с наполнителем равен:

G = У * H ^ D- . (3)

При надлежащем обосновании в собственный вес могут быть также включены вес надстройки, вес прилежащих призм грунта, нагрузки от стационарного оборудования и другие длительные технологические нагрузки.

Эпюра давления предельной нагрузки в пределах участка контакта (участок длиной l ) принята равномерной (среднее давление p ), поскольку определить точную конфигурацию эпюры распределения давления достаточно сложно, особенно в области больших деформаций. Существует приближенное численное решение В.В. Соколовского о неравномерном распределении предельного давления по поверхности, учитывающее также удельный вес грунта [7]. Разработанные на основе этого решения приближенные методы расчета устойчивости достаточно трудоемки и реализованы для узкого круга задач (для некоторых конкретных случаев составлены таблицы и графики [6]. В отношении устойчивости массивных сооружений методы проработаны только для случаев, когда сооружение опирается на специально подготовленную каменную или щебеночную постель, предварительно уплотняемую и обжимающую грунт и практически исключающую возможность значительных глубинных деформаций основания [2]. Точное строгое в математическом отношении решение получено только для «невесомой» грунтовой среды, моделируемой как линейно-упругий, идеально пластичный материал, отвечающий критерию Кулона-Мора.

В состоянии равновесия опрокидывающий момент равен произведению предельной нагрузки F max на плечо (расстояние d от подошвы сооружения до уровня приложения равнодействующей нагрузки). Уравнение восстанавливающего момента основано на следующих положениях:

– условно считается, что центр тяжести сооружения G находится на расстоянии половины диаметра D /2 от наружной грани сооружения;

– предполагается, что результирующая сила реакции давления R на грунт (в предельном состоянии равная весу сооружения G ) располагается на середине участка контакта: l'=l/2 . Такое допущение возможно, поскольку сдвиг равнодействующей ближе к наружной грани сооружения (обусловленный возможным ростом давления к краю сооружения при его повороте) компенсируется ее сдвигом в обратном направлении – к центру сооружения (ввиду того, что сооружение имеет круглое поперечное сечение). Из условия равновесия следует длина участка контакта:

l = - .                                                (4)

p

В результате восстанавливающий момент M 1 равен произведению гравитационной силы G на плечо, равное полуразности ширины сооружения (диаметра D ) и длины участка контакта l :

M = -D-G- = G(D-) .(5)

Уравнение равенства моментов запишем в виде

G ■ ^ = k ■ F_ ■ d .(6)

Тогда из условия равновесия с (1), (2), (3), (4) может быть получена зависимость для определения максимальной (предельной) опрокидывающей силы F max :

y H n D ³

F = - n-- max

8 • d • k

y H

c • ctg ф

1 + sin ф

- 1

1 - sin ф

• e ⁿ ‘8 ^ф

-

Формула (7) представляет собой теоретическую модель, функционально связывающую физические и физико-механические параметры грунта основания и размеры сооружения с максимальным удерживающим моментом, который может быть обеспечен сооружением без нарушения равновесия системы «оболочка – основание».

Выводы

В работе предложен метод определения предельных горизонтальных нагрузок на сооружения из заполненных оболочек из условия обеспечения несущей способности основания. В основе метода заложена теоретическая модель, разработанная в результате решения задачи о предельном напряженном состоянии грунтового основания с учетом развития полей скольжения. Модель опирается на точное и строгое в математическом отношении решение, и может быть использована для верификации численных расчетов, содержащих большее количество допущений, но более полно описывающих конструктивные особенности сооружения [1]. В качестве сопутствующего результата можно отметить также возможность использования простой теоретической модели, описываемой приведенными в статье формулами, на ранних стадиях проектирования. Теоретическая модель функционально связывает основные характеристики модели грунтового основания Кулона-Мора с основными размерами сооружения и предельной опрокидывающей силой. Поэтому модель позволяет осуществить быстрый предварительный подбор габаритов сооружения при заданных характеристиках основания из условия сохранения несущей способности грунта. При этом необходимо иметь в виду, что теоретическая модель не учитывает многие факторы, влияющие на работу сооружения: при проектировании, как правило, требуется определить предельную нагрузку с учетом допустимых перемещений для данного типа сооружения. После предварительного назначения габаритов следует перейти к более трудоемкой стадии вычислений с использованием численных моделей, которые позволяют провести детальные расчеты перемещений сооружения, деформаций основания, и напряжений в теле оболочки, наполнителя и грунте основания.