Метод расчета течения вязкой среды в каналах распылительной форсунки дизеля

С применением системы впрыска Common Rail, основанной на принципе подачи топлива к форсункам от общего аккумулятора высокого давления, связаны последние достижения в снижении расхода топлива, токсичности отработавших газов, уровня шума дизеля. Ее главное преимущество – широкий диапазон регулирования рабочего процесса, который достигнут за счет разделения процессов создания давления и впрыска, а также реализации многократной подачи топлива на протяжении одного цикла работы силовой установки.

Электрогидравлическая форсунка (ЭГФ) – основной элемент системы впрыска, который позволяет за счет электронного управления фазами и продолжительностью открытия иглы распылителя регулировать углы опережения впрыскивания и цикловые подачи топлива [2, 4].

Известно [1, 5], что пропускная способность, внутренняя геометрия и состояние гидравлических трактов (силовые и температурные деформации конструкции форсунки, изношенность трущихся пар, загрязнение внутренних полостей, закоксовывание распыливающих отверстий) оказывает влияние на параметры и характеристики впрыскивания топлива. Поскольку при работе приходится учитывать весьма тонкие эффекты (точно распределенная во времени и пространстве подача топливных смесей, сравнимая по длительности с временем формирования фронтов рас-пыливания), встает задача расчета нестационарных по времени потоков в гидравлических трактах с учетом их состояния и влияющих факторов [4].

Также ставится задача построения математической модели гидравлических трактов форсунки, учитывающей параметры формирования топливной струи и эффективности топливоподачи:

• -    реологию (вязкость и сжимаемость) топлива и ее зависимость от полей температур, давлений и скоростей течения в гидравлических трактах;

• -    профилирование элементов гидравлических трактов: жиклеров, камер, игл распылителя;

• -    нестационарный характер работы форсунки, переменное по времени сечение гидравлических трактов, влияние хода иглы на формирование струй топлива.

Решение этих задач предусматривает поэтапный расчет нестационарных процессов работы форсунки, в частности, переменного по времени течения вязкой среды, которой является распыляемое топливо, в канале игла – корпус распылителя при различных положениях иглы (рис. 1).

Это течение вязкой сжимаемой жидкости описывает система дифференциальных уравнений в частных производных (Навье – Стокса).

В цилиндрических координатах, при наличии осевой симметрии, эти соотношения принима- ют следующий вид:

1 dp + р дx

1 д ( дv

-^1 r r д r I д r

д 2 v_x д ² x

1 дp      1 д ( дvr ^ д2 vr--- + V--1 r—1 + , r р дx     r д r V д r ) д2 x

д ( v x r ) । ^{д (} v r r ) = 0 д x       д r

где v_x и v_r – осевая и радиальная компоненты скорости течения соответственно; x и r – продольная и радиальная координаты.

Система уравнений (1)–(3), дополненная уравнен и ем теплопроводности и зависимостями реологического состояния, может описывать поведение многокомпонентных смесей жидкостей и газов.

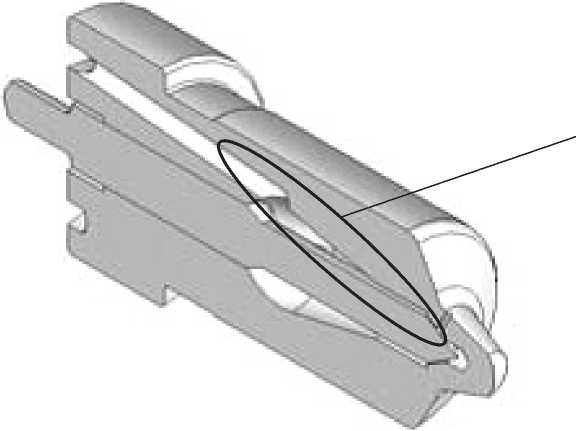
Область течения

Рис. 1. Канал игла-корпус распылителя [5]

Граничные и начальные условия для компонент с корости следующие (рис. 2, а):

Граница АЕ: vx = vнач = const, vr = 0 - задание входной скорости смеси;(4)

Границы ABCD и EFGH: vn = 0, vт = 0 - полное прилипание;(5)

Граница HI: vr = 0 – осевая симметрия;(6)

Граница DI: p = pцил (полное давление равно давлению в цилиндре).(7)

В настоящее время решения этих уравнений найдены лишь в некоторых частных случаях. Существует несколько ситуаций, обусловленных пр о стой геометрией, которые решены в аналитическом виде. Это стационарные течения в простых каналах – течение П у азёйля, Куэтта и др.. В остальных случаях используется численное моделирование [7, 8].

Решение этой задачи осложняется рядом факторов.

• 1.    Система Навье – Стокса нелинейна и ее решение сильно зависит от начальных и граничных условий.

• 2.    При превышении некоторого критерия (числа Рейнольдса, Re) выш е критичес к ого значения решение имеет хаотический (турбулентный) вид. При его уменьшен и и ниже критического решение принимает нехаотический (ламинарный) вид. Имеет место также исключительная чувствительность к изменению коэффициентов уравнен и я: при турбулентном режиме и при изменении Re на 0,05 % решения совершенно отличаются д р уг от друга.

• 3.    Для описания реальных течений приемлемую точность численного решения можно получить только при такой расчетной сетке, ячейки кото р ой меньше самого мелкого вихр я . Это требует очень больших затрат расчетного времени на современных компьютерах.

• 4.    Вблизи свободной поверхности жидкости при истечении из отверстия распылителя происходит резкое изменение скорости жидкости и ее плотности. Для того чтобы уловить эти изменения, необходима мелкая пространственная сетка. С ч итать во всей вычислительной области на такой сетке нельзя из-за ограниченности ресурсов ЭВМ, поэтому счет должен проводиться на неравномерной разностной сетке.

Экономичность, а следовательно, и быстродействие методов расчета таких задач значительно возрастают при простой форме расчетной области, в идеале прямоугольной в осевом сечении, допускающей построение высокоэффективных и апробированных разностных расчетных схем на ортогональных сетках. Ко всему этому надо добавить набор сервисных преимуществ, таких, как высокоточную интерполяцию, дифференцирование и интегрирование численного решения, простоту визуализации картины течения.

Поэтому существует устойчивый интерес к созданию методов построения ортог о нальных разностных сеток в области течения или, что то же с а мое - к их отображению на пара м етрические области (прямоугольники, параллелепипеды) и т. д. [10].

а)

б)

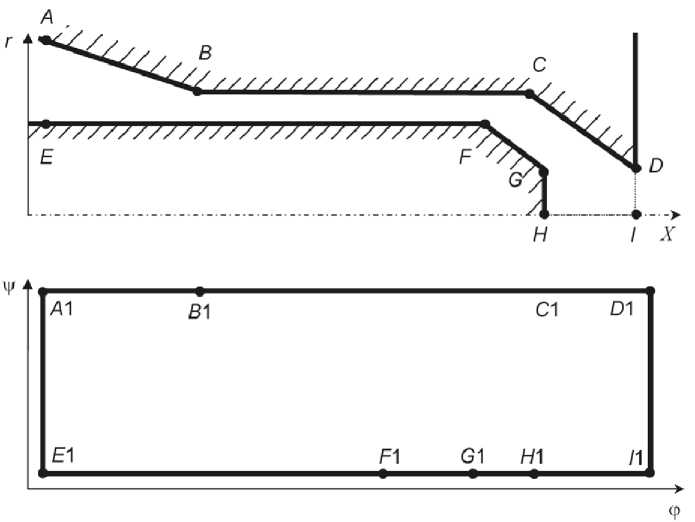
Рис. 2. Области течения (схематично): физическая (а) и параметрическая (б) плоскость

Поэтому, если будет найден достаточно универса л ьный метод преобразования исходной области течения среды в прямоугольник, с прямоугольной же расчетной сеткой, это позволит резко сократить расчетные затраты и повысить качество исследования и расчета кана л ов форсунок.

Перспективным методом выполнения такого преобразования координатных систем является его синтез путем построения конформного отображения. Однако разработанные до настоящего времени методы этого построения являются либо при г одными для ограниченного набора областей, либо построенными на итерационных алгоритмах, затратными с вычисл и тельной т о чки зрения и не дающими гарантий сходимости для более-менее реальных областей течения.

В данной работе предпринята попытка построения универсального метода численного синтеза конформного отображения, лишенного отмеченных выше недостатков.

Пусть ABCDIHGFE - выделенная для исследования область течения в осевом сечении гидравлических трактов распылителя. Введем в рассмотрение физическую плоскость с координатами x , r (см. рис. 2, а).

Пусть искомое отображение области ABCDIHG F E на прямоугольник A 1 B 1 C 1 D 1 I 1 H 1 G 1 F 1 E 1 (рис. 2, б) в параметрической плоскости с координатами ф , V реализуется функциями: ф = ф ( x , r ) , ф = ф ( x , r ) .

Для отображения области течения плоскости ( x , r ) решим следующие краевые задачи:

• а)    для V :

'Аф = 0 на: ABCDIHGFE

• V    = V 1 на: ABCD

• V    = ф ₂ на: EFGHI

  
  

• ^    = 0 на: AE

• 8    n

• = 0 на: DI .

Idn

Здесь ф 1 и V 2 — ординаты прямоугольника в параметрической области, задаваемые произвольно, А - оператор Лапласа: А = 3 2/ д х ² + d ²/ d r ² .

• b)    для ф :

'Аф = 0 на: ABCDIHGFE

Ф = Ф 1 на: AE

Ф = Ф ₂ на: DI

^ = 0 на: ABCD

• ³ n

2. Для краевых задач (8) и (9) решаются эквивалентные вариационные задачи:

^ = 0 на: EFGHI .

Idn

Здесь Ф1 - абсцисса левой стороны прямоугольника A 1 B 1 C 1 D 111 H1 G 1 F 1 E 1 в параметрической плоскости, задаваемая также произвольно.

Решение этих краевых задач сводится к последовательности следующих шагов, стандартных для метода конечного элемента [9].

1. Область течения ABCDIHGFE покрывается сеткой конечных элементов.

U 1 = 2 JJ (& ) + ( |2 ) dxdr ^ min, U 2 = 2 JJ (& ) + ( | у ) dxdr ^ min.

(10)

Опишем процедуру минимизации функционала U 1 для функции ф , задача минимизации функционала U 2 для функции ф решается аналогично.

3. Функция ф внутри каждого элемента аппроксимируется выражением вида

фe = N(e) {ф},

где

_N ( e )

- матрица-строка значений функций формы элемента в точке, { ф } — матрица-столбец

значений функции в узлах элемента.

Минимизируем функционал на множестве значений функции {ф} в узлах элементов. Вводя в рассмотрение матрицу производных {g}T

3ф 3ф dх dу

можем записать

U =JJ {g}T {g} ds ,

D или, суммируя по элементам в области течения:

U = EJ {g}T {g} ds .

E

Минимизация (13) приводит к системе

[K] {ф} =0.(14)

Система (14) состоит их линейных алгебраических уравнений с ленточной, положительно определенной матрицей [9]. Решая ее каким-либо численным методом, получим распределение значений функции { ф } в узлах элементов, покрывающих отображаемую область.

Краевая задача (9) для функции ф решается совершенно аналогично.

Из теории аналитических функций [6] известно, что односвязная область может быть отображена на прямоугольник с фиксированным соотношением сторон, или при заданной длине одной стороны – с определенной длиной другой стороны.

Поэтому, при заданных значениях функции ф : ф 1 и ф 2 , значение Ф 2 на правой стороне отображаемой области не может быть взято произвольным.

Воспользуемся соотношением, связывающим действительную ϕ и мнимую ψ части отображающей аналитической функции в любой точке области ABCDIHGFE , в частности – на сторонах AE и DI :

B ∂ψ ∂ψ

ϕ= - dx +    dy +ϕ 1 ,                                                            (15)

A ∂y∂x где ϕ1 – произвольная постоянная.

Интегрирование выполняется вдоль любого контура, соединяющего произвольные точки сторон AE и DI .

Таким образом, длина прямоугольника по координате ϕ :

• B ∂ψ ∂ψ

L =- dx + dy .                                                          (16)

∂y∂x

A

Приведенная методика, как видно из изложенного, снимает практически всякие ограничения по геометрии области течения в каналах распылителя.