Метод расчёта динамических характеристик гладких круговых цилиндрических многослойных оболочек при действии на них быстроизменяющегося внутреннего давления

Рассмотрим динамическое поведение тонкой трёхслойной круговой анизотропной цилиндрической оболочки, при воздействии на неё постоянного по величине внутреннего избыточного давления, распространяющегося вдоль её образующей с постоянным ускорением.

Рис. 1. Расчётная схема трёхслойной анизотропной круговой цилиндрической оболочки при постоянном давлении, распространяющимся с постоянным ускорением вдоль образующей оболочки

Предварительно сделаем некоторые допущения, которые упрощают расчёты, но незначительно влияют на конечные результаты. Первое допущение будет касаться сил внутреннего сопротивления, которыми будем пренебрегать, так как считаем, что частотный спектр внешнего воздействия далёк от резонансных частот цилиндрической оболочки.

Второе допущение касается инерционных сил в продольном направлении, которыми также можно пренебречь.

Третье допущение касается внешней нагрузки. Считаем, что она имеет осесимметричный характер, когда не учитываются круговые перемещения оболочки и их производные.

Согласно принятым допущениям расчётную схему можно представить так, как показано на рис. I.

Тогда с учётом сделанных допущений дифференциальные уравнения движения цилиндрической оболочки будут выглядеть таким образом [1]:

, д²и _ dw _ ди _      1     5⁴w d²w         ₂

Л--T^Cin--— 0; С]?--Н C77W Н— у Dil--т + ^л—у — 7ГГ PyClt ,         (1)

¹¹ д^ ¹² 9£      ¹² 9£   ²² г^{2 11} д^ ^р д?

где С_п, С, ₂, С₂₂, D_u - коэффициенты жёсткости цилиндрической оболочки;

7 д2

Wр = г Ср - Dp —2 ’ г ~ срединный радиус цилиндрической оболочки; Р^ - давление во внут реннем пространстве; а - ускорение, с которым передний фронт внутреннего избыточного давления распространяется вдоль образующей цилиндрической оболочки; и, w - соответственно продольные и радиальные перемещения срединной поверхности цилиндрической поверхности оболочки; £ - продольная координата цилиндрической оболочки; Ср - P\V\ * р^ * Р^ ; р - плотность материала; h, - толщина z-го слоя оболочки;

D_p ⁼ з(^1^1^{3 +} PiWh + ^³ -h³) + p₃(h³ -(h_v + h^)³)-!^^ + h₃ + h₃)-0,1Sh²(h_v -vh^ + h^y

Механика

Тогда из первого уравнения (1) получим — = — —w. Подставляя полученное значение для ^сн

— во второе уравнение (1), приходим к уравнению от одной неизвестной функции w(^,Z): 95

" а2

/"'2 Ai     д4 А

С_н ) г    9^

Для определения собственных частот оболочки рассмотрим это уравнение при отсутствии нагрузки. С учётом допущений, касающихся граничных условий закрепления краёв оболочки, собственные частоты определятся следующей формулой:

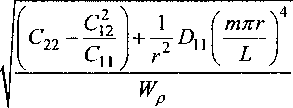
Так как нас интересуют низшие формы движения оболочки, и учитывая, что оболочка достаточно длинная, т.е. — > 2 J— , то вторым членом в числителе выражения (3) можно пренебречь.

Тогда можно считать, что со

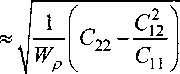
, и уравнение (3) примет следующий вид:

w + ro2w = Far,

где F = nr^P^IWp .

Уравнение (4) позволяет в первом приближении не учитывать условия закрепления краёв

оболочки [1].

При равноускоренном движении решение уравнения (4) можно записать в таком виде [2]:

Wpto

sin®/ Jr² cos tOTdr - cos mt ^т² smtOTdr о                       0

= w vcm

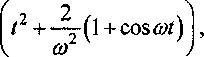
7СГ Руй           _ _                                                                                  ..

где wcm =............^--прогиб оболочки при полном давлении, т.е. при давлении, заполнившим все внутреннее пространство оболочки. Отсюда кд = -^- = г ч—y(l + cos®/). wcm to2

Анализ коэффициента динамичности показывает, что его величина не зависит от изменения

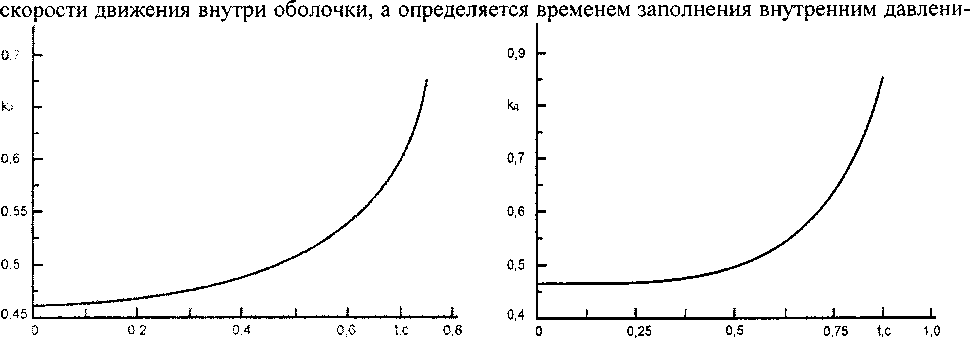
Рис. 3. Изменение коэффициента динамичности при минимально допустимом давлении и при максимальном времени заполнения внутреннего пространства цилиндрической оболочки

Рис. 2. Изменение коэффициента динамичности при максимально допустимом давлении и при минимальном времени заполнения внутреннего пространства цилиндрической оболочки

Машков Р.С. Метод расчёта динамических характеристик гладких круговых цилиндрических многослойных оболочек...

ем пространства оболочки и её собственной частотой. На рис. 2 и 3 показан характер изменения коэффициента динамичности в зависимости от времени для относительно коротких оболочек. Данные получены в программной среде MathCad для заданных эксплуатационных критических значений времени воздействия давления и его величины.

Анализ изменения коэффициента динамичности показывает, что максимальное его значение меньше единицы, поэтому динамическим усилением при дальнейших расчётах можно пренебречь. Это происходит потому, что корпус оболочки в силу своей инерционности и малого времени действия давления не успевает среагировать на эту нагрузку.

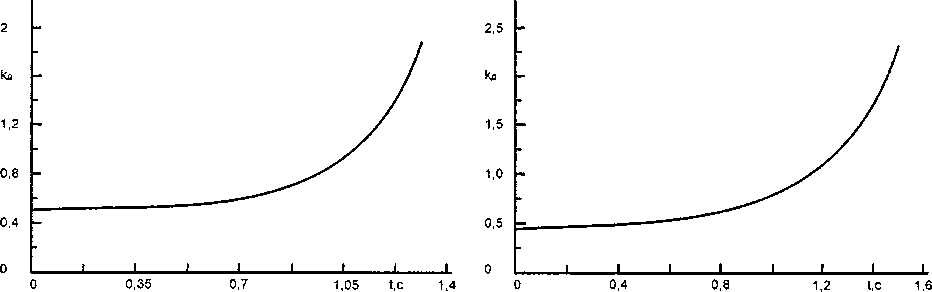
Рис. 4. Изменение коэффициента динамичности Рис. 5. Изменение коэффициента динамичности при максимально допустимом давлении и при при минимально допустимом давлении и при минимальном времени заполнения внутреннего максимальном времени заполнения внутреннего пространства цилиндрической оболочки пространства цилиндрической оболочки

На рис. 4 и 5 показан характер изменения коэффициента динамичности в зависимости от времени, в два раза превышающего предыдущие расчёты, т.е. для более длинных оболочек.

Анализ изменения коэффициента динамичности показывает, что при более длительном временном промежутке распространения избыточного давления внутри цилиндрической оболочки коэффициент динамичности существенно возрастает и особенности динамического поведения оболочки необходимо учитывать при расчётах.