Метод распознавания фигур с использованием Фурье-дескрипторов и нейронной сети

Введение. Распознавание образов является главной задачей в области машинного зрения. Многие задачи распознавания объектов на изображениях могут сводиться к распознаванию фигур - частному случаю распознавания образов. Эффективным и легкореализуемым способом представления фигур является использование фурье-дескрипторов [1]. В данной работе фурье-дескрипторы применяются совместно с нейронной сетью для решения задачи распознавания фигур.

Простые методы представления фигур на основе контура. Существующие методы представления фигур можно классифицировать следующим образом: это методы, основанные на контуре, и методы, основанные на области, пространственном домене и домене преобразования; информационно-сохраняющие (IP) и информационно-несохраняющие методы (NIP). В зависимости от способа обработки подходы к выделению и представлению фигур обычно разделяются на одномерные функции представления фигуры (one-dimensional function), аппроксимацию полигонов (рolygonal approximation), взаимосвязь пространственных признаков (spatial interrelation feature), моменты (moments), методы деления шкалы (scale-space methods), домены преобразования фигуры (shape transform domains) [2].

Для представления несложных фигур на основе контуров нередко используются комплексные координаты, функция расстояния, касательный угол, кривизна контура и фурье-дескрипто- ры. Все эти понятия (кроме фурье-дескрипторов) относятся к классу одномерных функций представления фигуры.

Комплексные координаты. Допустим, что изображение представляется в виде функции / ( x , у ) и P_n - ( x_n , у_п ), п - [1, N ] - множество точек на границе (контуре) фигуры. В этом случае z_n = x_n + iy_n называется комплексной координатой, которую можно использовать в качестве характеристики или дескриптора фигуры либо в качестве входных данных для фурье-преобразования. При этом контур обозначается в виде функции P_n = z_n , п =[1, N ].

Данный способ очень прост в реализации, но имеет ряд недостатков: получаемый результат является неинвариантным к перемещению, масштабированию и вращению. Чтобы комплексные координаты z_n были инвариантными к перемещению, они вычисляются с учетом центра тяжести (центроид): z_n =( x_n - x_g )+ i ( y_n - y_g ), где g =( x_g , y_g ) - центр тяжести фигуры.

Функция расстояния. Функция расстояния R_n для контура P_n =( x_n , y_n ), n =[1, N ] вычисляется как расстояние от неподвижной точки C ( x о , у о ) до каждой точки ( x_n , y_n ). В качестве точки С обычно выбирается центроид фигуры [2]:

^R n ^- 7^{( x} n - ^x о ) ^{2 + (} У п - У о ^{) 2} .

Функция расстояния имеет те же преимущества и недостатки, что и комплексные координаты.

Касательный угол. Каждый контур считается кривой линией, поэтому можно рассчитать угол наклона прямой, касательной к каждой его точке [2]:

- arctg

9 п

y n  ^У п - w

V ^xn ^{- x}n - w У

Здесь w - окно небольшого размера.

Несмотря на простоту реализации, данный метод имеет два существенных недостатка: чувствительность к шуму и прерывность. Для того чтобы избежать прерывности, определяется кумулятивная угловая функция ф _п - 9 _п - 9 _о , где 9 _о - касательный угол к случайной выбранной точке на контуре. До расчета этой функции часто применяется фильтр нижних частот. В настоящей работе кумулятивная угловая функция используется в качестве исходной функции для фурье-преобразования.

Фурье-дескрипторы. Фурье-дескрипторы получаются в результате применения фурье-преобразования к указанным выше одномерным функциям представления фигуры [3, 4]. Фурье-дескрипторами называются нормированные коэффициенты фурье-разложения. Предположим, что контур объекта обозначается непрерывной и периодичной функцией c ( t ), при этом

2 T                  2 T                    2—ГТ ak - — jc(t) cos(ktot)dt, bk - — jc(t) sin(ktot)dt, ck - aak + bk то                    то

( a_k - реальная часть; b_k - мнимая часть; c_k - фурье-дескриптор).

Фурье-дескрипторы устойчивы к перемещению, масштабированию и вращению объекта [2, 3], что позволяет использовать их для представления фигуры.

Алгоритм и его реализация. Процесс реализации системы включает два этапа: обучение и тестирование. Общая схема алгоритма показана на рис. 1. База данных для обучения содержит

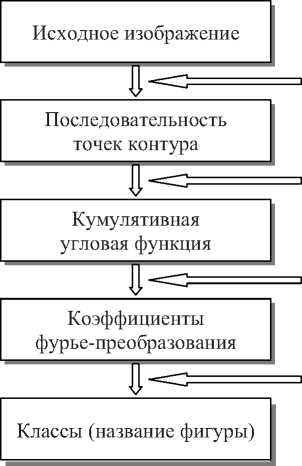
Рис. 1. Общая схема алгоритма

Извлечение контура

ПОПИВ 0ПИВП

□□□□□ а я и вл в

Рис. 2. База данных для обучения нейронной сети

20 "чистых" изображений одного объекта на черном фоне. Объекты делятся на следующие классы: окружности, треугольники, прямоугольники, полигоны (рис. 2).

Для выделения внешних граничных точек используется алгоритм соседних точек Мора (Moore’s neighbors) [5]. Результат выделения границы объекта с помощью алгоритма Мора представлен на рис. 3.

Выделенный контур сохраняется в виде массива точек P_n = ( x_n , y_n ), n = [1, N ], где N - количество граничных точек. Точки упорядочены по часовой стрелке. В каждой точке определяется угол наклона касательной линии к горизонтальной оси (угловая функция). Угловая функция меняется в диапазоне [0, 2 я ). Таким образом, она прерывна (резкий переход из 2 я в 0) и не может служить исходной функцией для фурье-преобразования. Для устранения этой проблемы используется кумулятивная угловая функция. Однако кумулятивная функция имеет ряд недостатков: она прерывна в последней точке контура и ее значения зависят от длины контура. Для того чтобы можно было применить фурье-преобразование, кумулятивная функция должна быть нормирована [3]:

Ф*(1) = ф| — t | +1 v 2л )

(ф - кумулятивная функция; ф - нормированная функция; L - длина контура).

Рис. 3. Выделение контура с использованием алгоритма Мора: а - исходное изображение; б - объект с выделенным контуром

б

а

е

*

Reto )

t

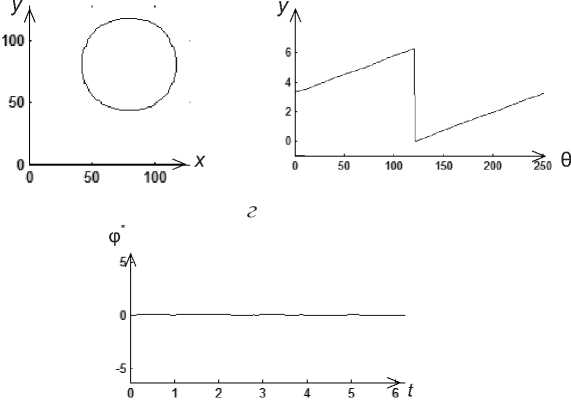
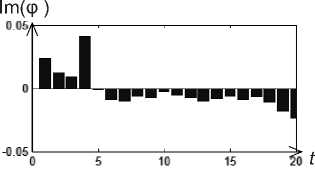
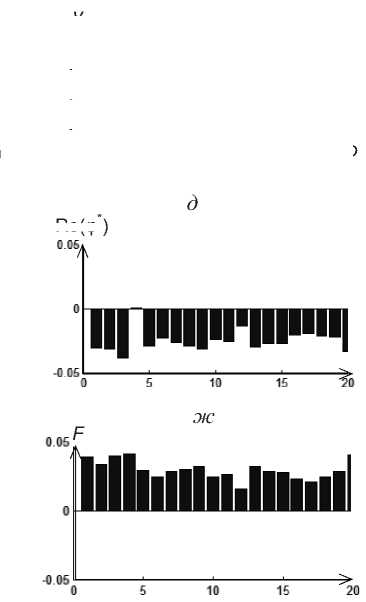
Рис. 4. Результаты фурье-преобразования для окружности:

а - исходный контур; б - касательная функция; в - кумулятивная угловая функция; г - нормированная кумулятивная угловая функция; д - реальная часть фурье-преобразования;

е - мнимая часть фурье-преобразования; ж - фурье-дескриптор

в

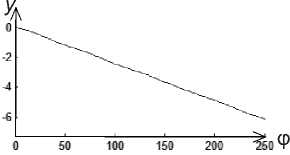
В результате применения фурье-преобразования к нормированной кумулятивной угловой функции имеем (рис. 4, д-ж ):

1 2 ^                                   2 ^

^Ck = ^ a k ^{+ b}k .

a_k =      ф ( t )cos( kt ) dt , b_k = ф ( t )sin( kt ) dt ,

4           ” 0

Полученные таким образом фурье-дескрипторы инвариантны к перемещению, масштабированию и вращению и могут быть использованы как входные данные для нейронной сети. Количество коэффициентов фурье-преобразования для нейронной сети будет зависеть от "сложности" фигуры. Эксперимент показывает, что для распознавания несложных тригонометрических фигур достаточно 15-20 коэффициентов. В данной работе используются 20 коэффициентов (дескрипторов).

Для распознавания фигур применяется традиционная многослойная нейронная сеть с обратным распространением ошибки, структура которой показана на рис. 5. В качестве функции активации используется обычная биполярная сигмоидальная функция. Для повышения скорости сходимости сети применяются следующие модификации: (Nguyen - Wldrow)-инициация, моментум, групповое обновление [6]. Эксперимент показывает, что 40 - 60 нейронов в скрытом слое дают лучший результат с точки зрения соотношения время обучения - сходимость. В данной работе используются 50 скрытых нейронов.

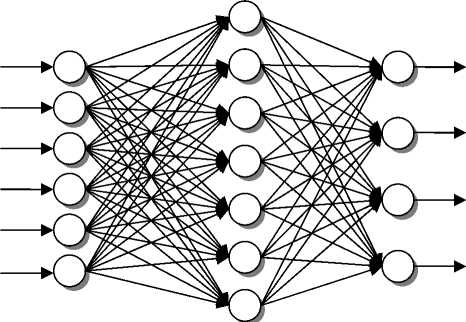
Скрытый слой -50 нейронов

Входной слой -20 нейронов

Выходной слой -4 нейрона

Рис. 5. Схема нейронной сети

Обсуждение результатов. Программа, реализованная на языке C# 2008, предоставляет возможность формирования базы данных для создания и обучения нейронной сети (многослойный персептрон), а также имеет отдельный интерфейс для проверки и тестирования работоспособности метода.

ИЕИПИ

ЕИЕИП

ВИИМ0

□в

Рис. 6. Тестовые изображения

На этапе обучения сеть сходится после 10 000 эпох со среднеквадратичной ошибкой, равной 0,001. Программа протестирована 50 раз с использованием тестовой базы данных, состоящей из 18 изображений (рис. 6). Частота появления ошибок составляет 0,1 %.

Для проверки эффективности работы алгоритма созданы другие базы данных тренировки и тестирования (рис. 7). Полученные результаты показали, что алгоритм позволяет распознавать достаточно сложные фигуры, состоящие из простых элементов (круг, эллипс, треугольники и т. д.) с высокой точностью: в результате обработки данных, показанных на рис. 7,

б после 30 тестов обнаружены две ошибки (частота ошибок - 0,15 %).

а

Рис. 7. Распознавание сложных фигур: а - обучение; б - тестирование

Выводы. Таким образом, создана программа для распознавания фигур на основе анализа контура с использованием фурье-дескрипторов и нейронной сети. Показано, что применение фурье-дескрипторов и нейронных сетей является эффективным методом решения задачи распознавания объектов. Разработанная программа способна распознавать сложные фигуры с высокой точностью.