Метод регуляризации решений бисингулярно возмущенной задачи в пространстве обобщенных функций
Автор: Акматов Абдилазиз Алиевич
Журнал: Бюллетень науки и практики @bulletennauki
Рубрика: Физико-математические науки
Статья в выпуске: 2 т.8, 2022 года.
Бесплатный доступ
При исследовании сингулярно возмущенных задач в случае изменения устойчивости вся работа производилась в пространстве аналитических функций. Естественно, возникнут вопросы, можно ли получить оценку решений сингулярно возмущенной задачи, не выходя на комплексную плоскость. В работе первыми полученными результатами являются решения сингулярно мотивированной задачи, не переходя в комплексную плоскость. Для этого разработан метод регуляризации в пространстве обобщенных функций и получены соответствующие оценки. Если выбрать начальную точку на устойчивом интервале, то вплоть до точки перехода асимптотическая близость решений возмущенной и невозмущенной задачи имеет порядок малого параметра ε. Проблема появится, когда точка принадлежит неустойчивому интервалу. Следовательно, до этого, работы переходили в комплексную плоскость. В таких задачах существует понятие времени запаздывания решений возмущенной и невозмущенной задачи. Линии уровня появятся в сложных плоскостях. В таких задачах существует понятие времени запаздывания решений возмущенной и невозмущенной задачи. Линии уровня появятся в сложных плоскостях. В особых точках эти линии имеют линии критического уровня. Поэтому невозможно выбрать начальную точку так, чтобы получить максимальное время задержки. Но асимптотическая близость решений возмущенной и невозмущенной задач возможна при ограниченных временных задержках. Если изучать решение в пространстве обобщенных функций, то можно выбрать начальную точку с максимальной задержкой по времени. А также, не переходя на комплексную плоскость, можно установить асимптотическую близость решений возмущенной и невозмущенной задачи. Для этого впервые разработан метод регуляризации решений сингулярно возмущенной задачи.
Дифференциальные уравнения, функционал, особая точка, бисингулярные возмущения, асимптотика, устойчивость, задача коши, носитель, регуляризация, финитность
Короткий адрес: https://sciup.org/14122895
IDR: 14122895 | УДК: 517.928 | DOI: 10.33619/2414-2948/75/01
Текст научной статьи Метод регуляризации решений бисингулярно возмущенной задачи в пространстве обобщенных функций
Бюллетень науки и практики / Bulletin of Science and Practice
УДК 517.928
В данной работе исследуем решения бисингулярно возмущенной задачи в случае смены устойчивости. Известно, что, не удается установить асимптотическую близость решений возмущенной и невозмущенной задачи в пространстве действительных функций [1–3, 5–7]. Поэтому, вся работа выполнялась, переходя к комплексной плоскости. В данной работе впервые разрабатываем метод регуляризации решений бисингулярно возмущенной задачи в пространстве обобщенной функции S '( R 1 ). Цель исследования. Доказать в пространстве обобщенных функций S '( R 1 ), асимптотическую близость решений бисингулярно возмущенной и невозмущенной задачи. С этой целью разрабатываем метод регуляризация решений бисингулярно возмущенной задачи в пространстве обобщенных функций S '( R 1 ). В данной работе впервые покажем суть метода регуляризации [4, с. 82–102] и приведем конкретный пример.
Материалы и методы исследования
Рассмотрим задачу sy' (t, s) = D (t) y (t, s) + s[f (t) + B (t) y (t, s)] (1)
У ( t o , s ) = У ° (2)
где D ( t ) = diag ( ^ ( t ), ^ ( t )), y ( t , s ) = colon ( y{ ( t , s'), y 2 ( t , s )), t e R 1, 0 < s - малый параметр, f ( t ) = colon ( f , ( t ), f 2 ( t ) ) , [ t o , T ] - отрезок действительной оси, t0 < T , C ” - пространство бесконечно дифференцируемых функций. Здесь S ( R 1 ) — пространство основных функций, S '( R 1) — пространство обобщенных функций. Действительные части собственных значений матрицы D ( t ) имеет устойчивые и неустойчивые интервалы.
Например, действительная часть собственных значений Re Л ( t ) < 0 , ( k = 1,2 ) в интервале t g ( -да , а 0) , то этот интервал является устойчивым, если Re Л ( t ) > 0 , ( k = 1,2 ) в интервале t g ( a 0 , +да ) - неустойчивым. Если Re Лк ( а 0) = 0 , тогда точка t = a0 является точкой перехода от устойчивого интервала к неустойчивому интервалу. Такие интервалы зависят от конкретных собственных значений матрицы D ( t ) . От устойчивого интервала выбираем начальную точку задачи Коши.
Взяв, формально £ = 0, получим невозмущенную задачу
D(t)~(t,0) = 0, D(t) ^ 0 .(3)
Уравнение (3) имеет единственное решение в пространстве S ( R 1 )
~ (t) = 0.(4)
Пусть выполняются условия:
Л (t) G Cда, Л2 (t) g Cда, Vt g Cда(Л (t) ^ 0, k = 1,2),
Определение 1. Обобщенной функцией называется всякий линейный непрерывный функционал на пространстве основных функций S ( R 1 ) и обозначается
+да
( y ( t , £ ), Ф ( t ) ) = j y ( t , £ ) Ф ( t ) dt .
-да
Определения 2. Финитным называют функции, которые обращаются в нуль функции вне некоторого конечного интервала.
t
Лемма 1. В области D , для функции e ( t , t 0, £ ) = y (0)( £ )exp 1 j D ( s ) ds , справедлива
k
t 0
следующая оценка
где с - некоторая постоянная.
Доказательство. Доказательство проводим в пространстве обобщенных функций S '( R 1 ), и составим, по определению функционала учитывая у (0)( £ ) = £ , получаем
+да — j D ( s ) ds
( E ( t , 1 0, £ ), ф ( t ) ) = £ j e"' 0
-да
ф ( t ) dt . Финитная функция изменит пределы интеграла в
окрестности особой точки
Определим норму функции,
S ( £ ) ij D ( s ) ds S ( £ ) 2j D ( s ) ds
( E ( t , t 0, £ ), ф ( t ) ) = £ j e '0 ф ( t ) dt = £ф ( t j) j e t 0 dt .
- S ( £ ) - S ( £ )
тогда ||( E ( t , 1 0 , £ ), ф 1 ( t ) J < 2 £S ( £ ) ф 1 ( t i )exp | 1 - F^0) | , где
lim S ( £ ) = 0, £ = o ( S ( £ ) ) . Отсюда видно, что доказано справедливости оценки (6) в
£ ^ 0
пространстве S ’( R 1 ). Лемма доказана.
t
t
Лемма 2. В области D , для интеграла E ( t, т , £ ) = j exp — j D ( s ) ds f ( r ) d r , справедлива
' 0
\
' 0
следующая оценка
IIE(t,T,£)|| < cS(£) , где lim S(£) = 0 , £ = o(S(£)), c - некоторые постоянные. £ ^0
+OT
Доказательство. Составим функционал ( E ( t , t , £ ), ф (t ) ) = j E(t , t , £ ) ф ( t ) dt . Из условия -от
+3 (£ £ финитности функции ф(t) имеем (E(t,r,£),ф(t))= jE(t,t,£)ф(t)dt. Из курса
-S (££ математического анализа известно, что если функция E(t,т,£) на интервале (t0,a0) монотонно возрастает и неотрицательна, а в интервале (a0, t) монотонно убывает и неотрицательна, тогда по формуле Бонне будет tt t - j D (s) ds j D (s) ds a 0
je£ f (r)dr = ea0 (j f (r)dr + j f (r)dr). Если функция f (t) интегрируема, тогда t0 t0
ir- t —j D (s) d s jj D (s)ds je^ f (tdr = e “0 [F(t) -F(t0)]. Функционал имеет вид определяющим с интегралом
' 0
S ( £ ) —J D ( s ) ds
( E ( t r £ ) ф - ( ' ) ) = j / a 0
S ( £ ) D ( s ) ds
£
F ( t ф ( t ) dt + F ( t 0) I e a 0 ф ( t ) dt . Оценим каждую слагаемую
-S ( £ ) -S ( £ )
S (£) -j D (s) ds j e a0 F(t)ф (t)dt
-S ( £ )
S ( £ ) —Re j D ( s ) ds
< F (0) ф ( tx ) j e £ a 0 dt
- S ( £ )
Последний интеграл стремится к
t нулю при £ ^ 0 , и Re j D (s) ds > 0 , F(0) ^ 0 .Оценим вторую слагаемую. Тогда 2). a 0
1 ' г i t
S ( £ ) j D ( s ) ds S ( £ ) j D ( s ) ds
F ( t 0) j e a 0 ф ( t ) d' = F ( ' 0 ) ф ( t [) j e a 0 dt , который стремится к нулю при £ ^ 0 . В
- S ( £ ) - S ( £ )
общем случае норма интеграла || E ( t , т , £ ) ф ( t )|| < c S ( £ ). Отсюда видно, что оценка (7) доказано.
Лемма полностью доказана.
Тогда имеет место следующая теорема.
Теорема. Пусть выполняются условия (5). Тогда задача (1), (2) имеет единственное решение и для нее справедлива оценка
||у(',£)|| < CS(£) , где а(£) ^ 0, £ ^ 0, t g C, C — постоянное число.
Доказательство. От задачи (1), (2) приходим к эквивалентному уравнению:
y ( t , e ) = y 0 ( e ) ) E ( t , t 0 , e ) + j E ( t , r , e ) [ f ( r ) + B ( r ) y( r , г ) ] d r , t 0
где
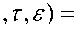
t
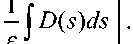
J
\ Г
Уравнение (9) будем решать методом последовательных приближений:
y0(t,г) ^ 0, y 1(t,г) = y0(e)E(t,tо,г) + jE(t,r,e)f (r)dr , t 0
t
У п ( t , e ) = y 1 ( t , e ) + j E ( t , r , e ) B ( r ) y n - 1 ( r , e ) d т , где t 0
Решение рассмотрим в R 1, поэтому имеем единственный путь интегрирования.
Учитывая лемму 1 и лемму 2, производим оценку последовательных приближений
t
у] (t, e) = y0 (e)E(t, 10, e) + j E(t, r, e)f (r)dr . Для первого приближения верна оценка t 0
||yx (t, e)|| < c8(e), где c — некоторая постоянная. Далее, для второго приближения аналогично получаем, ||у2 (t, e)|| < c8(e) + (c8(e))2 где c — некоторые постоянные. Предположим справедливость следующего неравенства ||yn(t,e)|| < c8(e) + (c8(e))2 +... + (c8(e))n, гдеc — некоторые постоянные, n g N. Справедливость оценки (8) доказана.
Теперь докажем сходимость последовательных приближений. Имеем ||У 1 ( t , e )|| < c 8 ( e ) < 1 , | y 2 ( t , e ) - у 1 ( t , e )|| <( c 8 ( e ) ) 2 < 1,
||y 3 ( t , e ) - у 2 ( t , e )|| < ( c 8 ( e ) ) 3 < 1, | y n - 1 ( t , e ) - У п - 2 ( t , e )|| < ( c 8 ( e ) ) n - 1 < 1.
Докажем справедливость оценки ||yn (t, e) - yn4 (t, e)||. Имеем что разность решений верна |yn (t, e) - Упч (t, e)|| < (c8(e))n < 1 .Построим ряд да
E ( y k ( t , e ) - y k - 1 ( t , e ) ) .
k = 1
Если ряд (10) сходится равномерно, то последовательность {yn (t, e)} сходится равномерно.
Докажем равномерную сходимость ряда (10). Имеем да
E ( Ук ( t , e ) - yk ( t , e ) )) k = 1
да
< EI y k ( t , e ) - y k - 1 ( t , e )ll = I y 1 ( t , e ) - y 0 ( t , e )1 + k = 1
+
||y 2 (t , e ) - y 1 ( t , e ) + ... + Iy n ( t , e ) - У п - 1 ( t , e )|| + ... = c 8 ( e ) + ( c 8 ( e ) ) 2
+
В рассматриваемой
+ ... + ( c 8 ( e ) ) n + ... = c 8 ( e ) x
r1
L 1 -(c8(e)) J
области || yn ( t , e )|| < c 8 ( e ) x
r Ucmr 1^ 1 - c8(e) J
,и при
n ^ да получим
||y ( t , e )|| < c 8 ( e ) .Теорема доказана.
На основе доказанной теоремы видно асимптотическую близость решений (8) и (4).
Приведем пример. Пусть матрица-функция D ( t ) имеет сопряженные собственные значение \ ( t ) = t + i и Л2 ( t ) = t - i .Определим действительную часть собственных значений Re ^ ( t ) = t , ( k = 1,2 ). Действительная часть собственных значениях устойчива в интервале t е ( -ю ,0 ) , и неустойчива в интервале t е [ 0, +® ) . Точки перехода t = 0 также входит в неустойчивом интервале. Потому, что в окрестности точки t = 0 и самой точке не определено устойчивость. В качестве начальной точки можно взять -ю < t 0< 0. Собственные значения комплексно-сопряженные, поэтому достаточно исследовать \ ( t ) = t + i . Полученные оценки выполняются аналогично. Задачи (1), (2) сведем к эквивалентной задаче вида (9), учитывая, что функция f ( t ) интегрируема в отрезке t е [ t 0, T ] , ( t 0 < T ) в векторном виде:
t
y(t, s) = y 0(s)E(t, 10, s) + j E(t, t, s)[f (t) - B(t)y(t, s)]dr . Для одного собственного t 0
-
1- ( ( t + i ) 2 - ( 1 0 + i ) 2 ) p — ( ( t + i ) 2 - ( t + i ) 2 )
значения имеем yx (t, s) = y^(s)e2s +j e2s f (t)dr . Используя лемму 1, t0
—( ( t + i ) 2 - ( 1 0 + i ) 2 )
оценим первую слагаемую y[ (s)e2s . Здесь y[ (s) = s можно заменить, учитывая условия устойчивости собственных значений. Тогда составим функционал в пространстве
S ’( R ‘)
— (( t + i ) 2 - ( t 0 + i ) 2 ) s e 2 £
I
+W
,ф( t) = s j
’ 2 ( ( t + i ) 2 — ( 1 0 + i ) 2)
e 2 s ф ( t ) dt . Определим абсолютную величину
J -'
функционала f ((‘+i)2 -(‘0+i)2 )
s e 2 s
I
, ф ( * ) J
величина функционала
среднем к функционалу
+ю - ( t 2 - 1 02 )
-
< s j e2 s ф (t ) dt .
-ю
f T ((t+i )2 -(t 0 + i )2 )\ se2s ,ф( t)
IJ
-
—( ( t + i ) 2 - ( t 0 + i ) 2 )
s e2 s , ф ( t )
IJ
Функция ф ( t ) финитна, поэтому абсолютная
+ s 1 2 ,2
( t - 1 0 )
-
< s I e 2 s ф ( t ) dt . Применим теоремы о
-
- V s
+ s ± ( 1 2 - 1 0; )
< s^ ( t j ) j e 2 s dt ^ 0, при s ^ 0 . Теперь
- s
p “( ( t + i ) 2 - ( t + i ) 2 )
оценим интеграл I e2s f (t)dr и составим функционал в пространстве обобщенных t 0
Г ~ ( ( t + i ) 2 - ( t + i ) 2 )
функций j e 2 s
x
+'
t
f T ) d T , ф ( t ) = j j e
J
-ю
\ t 0
—( ( t + i ) 2 - ( t + i ) 2 )
2 s f ( t ) d r ф ( t ) dt . Найдем абсолютную
J
величину
функционала
f2 X ( ( t + i ) 2 - ( t + i ) 2 ) ^
j e 2 s f i ( T X ф ( t )
1 1 0 J
+ю/ t
<1,
'A t 0
^( t 2 - T 2 ) e 2 s
f , ( t ) d r ф (t ) dt . А теперь J
определим
финитности
V. -L(( t + i ) 2 - ( t + i ) 2 ) ^
j e 2 s f 1( T ), ф ( t )
1 1 0 J
+ dSf t 1Z2 2. A
С Г — ( t - t )
-
< j j e 2 s f - ( t ) d T ф ( t ) dt .
-
- ^ 1 0 J
функций ф ( t ) :
Интеграл запишем в виде:
Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №2. 2022 t 1 2 2Л 012 2ч t 1 2 2ч
-—т 2
2 £ в интервале t е [ t 0,0 )
( t — т ) ( t — т ) ( t — т )
J e2 £ f ( т ) d т = J e2 £ f ( т ) d т + J e2 £ f ( т ) d т . Функция e
t 0 t 0 0
монотонно возрастает и неотрицательная, а в интервале t е ( 0, t ] монотонно убывает и неотрицательна. Видно, что выполняется условия формуле Бонне. Интеграл можно записать
t в виде J e t0
1 2 1 2 t t 1 2 _2ч 1 ,2
( t т ) t ( t т ) t
2 £ f ( т ) d т = e2 £ J f ( т ) d r . Интегрируя J e2 £ f ( т ) d r = e 2 £ [ F ( t ) — F ( t 0) ] .
t 0
t 0
Подставляя, этот интеграл к функционалу получаем
следующие интегралы
^f 4t 2 — т 2 )
J e 2 £
\ t 0
A f^T) dT,^ t) = J
—t 2 р — t 2
e 2 £ F ( t ) ф ( t ) dt + F ( t0 ) J e 2 £ ф ( t)dt .
Оценим
функционал.
—>! £
—V £
Тогда, учитывая теорему
о среднем, вычислим
интеграл
и получим,
■ ^^2 V £
J e2 £ F ( t ) ф ( t ) dt < e ф ( tx ) J F ( t ) dt = e ф ( t{ ) [ f ( 4s ) — F ( — ■ ) ] . Отсюда имеем
оценку равную
-у/ £
-у! £
c
-
некоторые
постоянные.
Второе
слагаемое
функционала
•V £ 1 2 ££
F ( 1 0 ) J e ^'^(. t ) dt = F ( 1 0 ) ф 1 ( 1 1 ) J
—V £
—
■ -12 г e2£ dt. Получаем оценку равную cd £ , где c - некоторые ■
постоянные.
В итоге для первого приближения имеем
|( y 1 ( t , £ ) ф ( t ) < ( c 44 ф ( t ) ) , отсюда видно что
IУ[ (t, £)| < c4~£ .А и для F (t) имеем |y2 (t, £)| < c4s , где c некоторые постоянные.
Последующие приближения определяются аналогично.
Результаты и обсуждение
Из выше доказанных лемм и теоремы видно, что в пространстве обобщенных функций S '( R ' ), можно установить асимптотическую близость решений бисингулярно возмущенных и невозмущенных задач.
Метод регуляризации обсуждено на основе примера на научном семинаре кафедры математического анализа под руководством профессора С. Каримова.
Выводы
Подведя итог, можем сказать, что последовательность { yn ( t , £ } равномерно сходится к некоторой функции y ( t , £ ) , которая является решением уравнения (1). Когда собственные значения матрицы имели устойчивый интервал, то можно доказать асимптотическую близость решений бисингулярно возмущенной и невозмущенной задачи. Появится вопрос: можно ли установить асимптотическую близость решений возмущенной и невозмущенной задачи когда, собственные значения матрицы не имели устойчивой интервал. В этом направлении продолжим исследовании.


