Метод решения обратной задачи идентификации функции источника с использованием преобразования Лапласа

Обратные задачи идентификации источника, возникают при исследовании различных процессов, связанных с переносом и распределением вещества, или энергии внутри тела. [1-3]. Математически в линейном приближении эти процессы описываются уравнениями параболического типа, с неизвестным неоднородным слагаемым, называемым функцией источника, и дополнительно известными начальными и граничными условиями. Для получения устойчивого численного решения рассматриваемых задач используют различные методы регуляризации [4-8].

В статье предложен метод решения обратной задачи идентификации функции источника, основанный на. применении прямого и обратного преобразований Лапласа. В подходах, использующих преобразования Лапласа, как правило, после выполнения прямого преобразования получают устойчивые решения с помощью методов регуляризации, а затем уже для этих решений применяют обратное преобразование (см., например, [9, 10]). Основная трудность при таком подходе состоит в том, что численная реализация обратного преобразования Лапласа, сильно неустойчива. В данном исследовании предложен другой под- ход, обобщающий результаты, представленные в работе [И]. В результате его применения сначала получают интегральное уравнение, устанавливающее явную зависимость функции источника от известных граничных и начальных данных, а затем уже для решения этого уравнения используют методы регуляризации. Аналогичная идея была использована в работах [12, 13] для решения обратной граничной задачи.

Практическая реализация предложенного подхода предусматривает разработку численного метода решения полученного интегрального уравнения. С разработкой и исследованием устойчивых численных алгоритмов связаны работы многих исследователей, например, [14-17]. В данном исследовании в качестве одного из возможных методов решения используется численный метод, основанный на схеме Лаврентьева с апостериорным выбором параметра регуляризации.

Статья имеет следующую структуру. В первом разделе приведена постановка задачи а также дополнительные свойства и ограничения на рассматриваемый класс функций. Второй раздел посвящен построению основного интегрального уравнения. В трерьем разделе предложен численный метод решения полученного уравнения В четвертой части статьи приведены результаты вычислительного эксперимента, основными целями которого являлись проверка эффективности предложенного подхода к решения задачи идентификации, основанному на преобразованиях Лапласа, а также получение экспериментальных оценок погрешностей регуляризованных решений. В заключении сформулированы итоговые выводы, полученные в результате проведенных исследований, а также указаны основные направления дальнейших исследований.

1.    Постановка задачи

Рассмотрим следующую задачу:

u t = au xx + f(t), x € (0,1), t> 0,                            (1)

u(0, t) = u(£, t) = u(x, 0) = 0,   x € [0,1] , t > 0,

ux(0,t) = g(t), t > 0, где функция f (t) подлежит опреле.тепито. Полагаем, что g € C2+ч[0, T] при всех T > 0. а ^ € (0,1) II существуя>т константы M,m такие. что |g(t)| — Memt для лтобого t € [0, T] при всех T > 0. Известно, что при некотором g(t) = go(t) существуют точное значение fo(t) и фу1 шипя uo(x,t). удовлетворяют пая (1)-(3) при f (t) = fo(t). но в место go известны некоторые приближения д§ и уровень погрешности 5 > 0 такие, что \\д§ — gohc(oT) — 5-Требуется сначала определить функцию f^t) € C1+ч(0, T) при всех T > 0, а затем найти u^ (x, t) € H2,1((0,1) х (0, T)) при T > 0, удовлетворяющую (1)-(3). Единственность решения рассматриваемой задачи (1)-(3) была доказана в работе [18].

В данном исследовании предлагается разделить решение обратной задачи идентификации источника на два этапа. Первый этап заключается в сведении исходной задачи идентификации функции f (t) к решению уравнения Вольтерра первого рода, характеризующего прямую зависимость функции f (t) от граничных условий. На втором этапе осуществляется численное решение полученного интегрального уравнения и по результатам решения вычисляются значения функции u^(x,t).

2.    Построение интегрального уравнения

Сведем задачу (1)-(3) к интегральному уравнению. С этой целью найдем решение прямой задачи, предположив, что искомая функция f (t) нам известна, то есть рассмотрим следующую задачу задачу:

u t = au xx + f(t), x € (0,1), t > 0,

u(0, t) = u(£, t) = u(x, 0) = 0,   x € [0, £],    t > 0.

Найдя решение u(x, t) этой задачи, и, выполнив затем соответствующие преобразова ния, получим уравнение, связывающее f(t) и ux(0,t) = g(t).

Полагаем, что существуют C, C > 0 i1 ^о,^ > 0 такие. что |u (x, t)| < Ce^°t 11 |f (t) | < Ce^t выполнены при x € [0, £] и при всех t € [0, T] для любого T > 0. Дополнительно полагаем, что функция f(t) удовлетворяет условиям Дирихле для любого t € [0, T] при всех T > 0. Тогда, следуя результатам, представленным в работе [19], применим прямое преобразование Лапласа в задаче (4), (5). Обозначив изображения функций u(x,t) и f (t) как u(x,p) и f (p) соответственно, получаем, что операторное изображение прямой задачи

(4), (5) имеет вид:

d2u p

^^^^.

^{-f (}p),

- dx2   a

u(0,p) = u(£,p) = 0.

Решение этой задачи определяется формулой:

uVp) =

_/(p) sh (VT') — sh (V?x) — sh (VT(< — x)) ^p                                                    sh^{\biggl(\sqrt{} p} a\ell^\biggr)

.

Лемма 1. Решение u (x, t) задачи (4), (5), имеет вид:

„ „ sin ( ^mM rxlt

-       2m + 1

m=0о sh \surdpx

Доказательство. Из теоремы , доказанной в 13 следует, что функцию ^ (x,p) = у Д sh p можно представить в виде:

2 ^

^ (x,p) = x + -

(-1)m

m

sin (-mx)

p p + m2-2 .

Тогда, имеют место следующие соотношения:

sh (Vpx) = x , 2 V^ (-1)™ • „ (-mx A P sh (VP^)   ^ + - m=1 m si £ P + T sh (Vp(^ — x))   ^ — x 2 £ (—1)m . /-m(£ — x) A p sh (VP^)   = ”T+ + - xL m sin £   ) p + m^a • a                     m=1                                   C2

Учитывая сходимость рядов в (8), выполним соответствующие преобразования в (6), получаем:

u(x,p) = 4& E

\pip

sin ^2^ +1 -x^

2m + 1    p +

p

(2 m +1) ² ^ ² a * £ 2

Принимая во внимание свойства функции f (t), применим обратное преобразование Лапласа к обеим частям (9). Далее, используя теорему о свертке [19], получаем:

u^t) = - X

sin (^ -x)

2m + 1

v ² (2 m + 1)² at £ 2

t

I f ( t )e ^m^ d_T* 0

Сходимость ряда (7) для любых x E [0,6) nt E [0, T) следует из теоремы Вейерштрасса и следующей оценки:

sin (2^-xj

2m + 1

v ²(2 m + 1)² at £ 2

t

I^{f (}T )e

V ² (2 m + 1)² aT £ 2

d\tau

\leq

— _o V ² (2 m + 1)² at

1      - , 2(2„₁+1)2 at    C£²e ¹ £2 *   + pt           c^t

(2m + 1)e           (-2(2m + 1)2a + 62^) — -2a(2m + 1)3 *

Обозначим Q t = (0,6) х (0, T) при T >  0. В силу того, что численное решение зада-чи(1)-(3) может быть найдено только в ограниченной области Qt, и, учитывая, что для его построения нам потребуются только значения u_x(0,t), мы можем сформулировать следующий результат.

Теорема 1. Пусть решение u(x,t) задачи (4), (5) определено формулой (7), тогда имеет место следующее представление

4 vv2 (2m + 1)2 at               тг2(2т + 1)2ат ux(0,t) = 6 e--£2----0 f (t)e----£2---- d\tau

при всех t E [0, T ] для каждого T >  0. и для любых 5 >  0 1i e >

0 найяется N такое, что

4 E -

\ell ^e

v ²(2 m + 1)² at ) £ 2

t

У ^{f (} т)e

v ² (2 т +1)² ат £ 2

d\tau - gdelta

< e + 5*

C (0 ,T )

Доказательство. Рассмотрим ряд

\infty

4 E co=( =

2m + 1 \ell

\pix e-

v ² (2 m + 1) ² at £ 2

t

У ^{f (} т )e

v ² (2 m + 1)² ат £ 2

d\tau.

(Ю)

Применяя рассуждения,

аналогичные

приведенным в лемме 1,

получаем:

cos ^

2m + 1 \ell

\pix

t

У ^{f (} т )e

V ² (2 m + 1)² at

e          £ ²

v ² (2 m + 1)² ат £ 2

d\tau

C6² e ^t

-2a(2m + 1)2

\infty

Из сходимости ряда X (2m+i)2 ’ а также из теоремы Вейерштрасса следует сходимость m=0 к ряда (10) при всех x Е [0,7). Таким образом, используя свойства сходящихся рядов, получаем:

4        / ux(x,t) = 7 cos =

2m + 1 \ell

t

)v2 (2m + 1)2 at e                f (t )e

v ² (2 m +1) ² ат

ё ²     dT.

Далее аппроксимируем функцию u x (0,t) конечным рядом. Тогда, (10) для любого Е >  0 пандется N такое, что

в силу сходимости ряда

N ^t

4 \—A _ ’ ²⁽² m + ^1)2a t

7 2^ e      ё2        f (t)e m=0           0

v ² (2 m + 1) ² ат

^ё 2      dT - ux(0, t)

< \varepsilon.

(И)

Принимая во внимание условие (3), получаем требуемое неравенство.

Таким образом, мы можем сформулировать основной результат. Из теоремы 1 и условия (3) следует, что неизвестная функция источника f (t) может быть определена при решении следующего уравнения:

4 E — \ell^e

v ² (2 m + 1) ² at ё ²

t

I f ( t )e ( ^ё + ) dT = g (t) 0

при условии, что вместо точно заданной функции g (t) известны g § (t) и 5 > 0 такие, что \\g (t) - go (t)Н < 5 при всех t Е [0,T].

3.    Численный метод

Определив K(t,T ) при всех t Е [0; T ] соотношением

N

Kn (t - T) = 4 E e-(t-)- и при условии, что g (0) = 0, мы можем рассматривать уравнение (12) как уравнение Воль-терра первого рода:

t

Af = I K n (t — t )f ( t )dT = g(t).

Единственность решения этого уравнения при всех t Е [0, T ] для любых T >  0 была доказана в [20]. Решение уравнения (13) возможно получить, применяя различные численные методы, но выбор наиболее оптимального метода решения уравнения (13) не является целью даннного исследования, поэтому нам достаточно рассмотреть один из возможных методов решения задачи идентификации. В качестве такого метода мы используем вычислительную схему, основанную на методе регуляризации Лаврентьева.

Построение численного решения задачи (1)-(3) осуществим в два этапа. На первом выбирем количество слагаемых в (11). Для этого ортогонализуем систему функций v ² (2 m +1) ² a ^N                                                                           N

|e    ё2    | для каждого N > 2 и t Е [0,T]. Обозначим через {^m(t)}o полученную ор- тогонализованную систему функций. Найдем коэффициенты {gm(t)}N в разложение функции gg (t) по этой системе, используя формулу:

T

^g 8m —

/

g s ^(т ) ^m ^(т )

d\tau.

N

Полагаем g N§ — ^2 9 6m ^ (t)- Перегруппировав слагаемые в последнем соотношении, m=0

^N       _ 77 2 (2m + 1)2 a                    N получаем gN§ — 2L cme    12    , гДе {cm(t)/o — коэффициенты, полученные после ne- m=0

регруппировки.

Далее при каждом значения N вычисляем величину hN по формуле hN —

4 Л

_\ell        c m e

7 ² (2 m + 1)² a

^Г2     - g s

C ([0,T ])

Используя условие 6 <  h N <  6 + е при е ^ 0, находим N. Заметим, что при таком подходе величина N может принимать только небольшие значения.

На втором этапе получаем численные решения уравнения (13), используя вычислительную схему, основанную на методе регуляризации, предложенном в [21]. Согласно этому подходу, регуляризованное решение поставленной задачи определяется из уравнения:

Af + af — g s ,                                  (16)

при соблюдении условия ||Af — gg|| < 6 + е при е ^ 0. Выбор параметра а можно осуществить с помощью различных подходов. В данном исследовании параметр а выберем следующим образом. Предположим, что для некоторого «0 было получено решение f^ урав-P нения (15). Вычислим P — HAfU и M — м--ту. Затем используем идею, предложенную в \bigm\|fdelta \bigm\| работе [22], согласно которой параметр регуляризации определим с помощью функции

ф⁽«) ^— и^а(аЕ+ A h N ^)-2g g - f 11 +—+ "g^ ^N , а а²

где 0 < а <  M. Для выбора параметра, а мы на каждом этапе при фиксированном N определяем наименьшее по а значение функции Ф(а). В работе доказано [22], что при таком подходе, мы получаем единственное обобщенное квазиоптимальное значение а. Таким образом, для численного решения уравнения Вольтерра мы получаем итерационную вычислительную схему, где параметрами регуляризации являются количество слагаемых N в ряде (11) и величина а.

4.    Вычислительный эксперимент

Подход, позволяющий с помощью преобразований Лапласа свести решение задачи идентификации источника, к интегральному уравнению, послужил основой для разработки численного метода, и проведения вычислительного эксперимента. Основными целями эксперимента. являлись оценка, эффективности данного подхода, а. также получение экспериментальных оценок погрешностей численных решений. Эксперимент проводился для тестовых функций с использованием равномерной сетки (x i , t j ) из (n + 1) х (r + 1) узлов. В качестве

Таблица 1

Экспериментальные погрешности Afopt

\delta f1 f2 f3 f4 f5 f6 0,02 0,0367 0,7471 0,0412 0,0522 0,1112 0,0811 0,05 0,0749 0,8551 0,0838 0,0732 0,1562 0,1672 0,1 0,1878 0,7878 — 0,1723 0,1885 0,2060 тестовых были использованы следующие функции:

f i = te t , f2 = (1 - t) e^- 2 t, f = t (e- t — e^-1 ) , f 4 = sin (3^t) e^-t,

,      • мп -t г \ sin(5^t) — 2.5t2, t E [0;0.5), f5 = srn(1Me t, f6 = cos(5^t), t E [0.5; 1]

Основные этапы вычислительного эксперимента состояли в следующем.

Этап 1. Для тестовой функции fk (t) находим решение Uk (x, t) прямой задачи (4), (5), используя конечно-разностные уравнения. Затем моделируем значения g(t j ) в узлах (xi, tj), с помощью конечно-разностных аппроксимаций частных производных. Далее задаем возмущение правой части уравнения (13) так, что g § (t j ) = g(t j ) + e g (t j ), г де e g (t j ) является случайной величиной равномерно распределенной на [g(tj) — 5; g(t j ) + 5].

Этап 2. Находим решение fl интегрального уравнения (13) с помощью предложенного численного метода. Для аппроксимации интегралов используем квадратуру правых прямоугольников. После построения fl вычисляем величину Af = ||f1 — fk ^c(ot )•

Этап 3. Подставляя найденые fl в (4) и используя (5), находим иЦ и вычисляем Au = IH^{( x,t) —} uk ^(x,t)hL 1( Q_T )•

Этап 4- Для исследования влияния параметров N и а на устойчивость метода повторяем этапы 2, 3 для различных N и а и вычисляем Af при каждом повторе.

Заметим, что подходы, используемые для моделирования возмущенных данных и вычисления Au обусловлены физическим смыслом задачи и спецификой проведения расчетов, основанных на экспериментальных данных, когда известен только максимальный уровень шума, а другие характеристики шума носят случайный характер и требуется, с одной стороны, избежать излишнего усложнения вычислительной процедуры, а с другой стороны, получить численное решение, имеющее приемлимый уровень погрешности.

Результаты вычислительного эксперимента приведены в таблицах и представлены на рисунках. Средние значения Afopt и A_Uopt, полученные при различных 5 и оптимальных значениях параметров N (5) и а (5), представлены в таблицах 1 и 2, а соответствующие им графики и поверхности представлены на рис. 1-6. Таблицы 3-8 содержат результаты исследования влияния параметров N и а на погрешность решений при выбранном подходе к моделированию возмущенных данных. В статье представлены результаты этих исследований, полученные при 5 = 0, 02.

На всех рисунках используются одинаковые обозначения. Одномерные рисунки иллюстрируют графики функций источника f. Обозначение «model» соответствует графикам тестовых функций fk, к = 1, 6 а графики решений fl уравнения (15) обозначены как fg.

Таблица 2

Экспериментальные погрешности Auopt

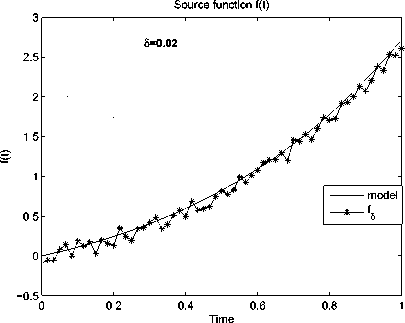
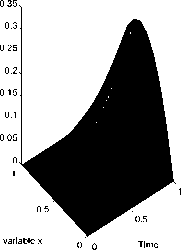
Рис. 1. Результаты численного решения задачи (1)-(3) для функции fi(t)

Exact Solution

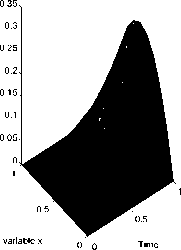
Verification

\delta	f 1	f 2	f 3	f 4	f 5	f 6
0,02	0,0076	0,0174	0,0125	0,0169	0,0188	0,0215
0,05	0,0218	0,0230	0,0251	0,0198	0,0202	0,0243
0,1	0,0267	0,0272	—	0,0274	0,0291	0,0304

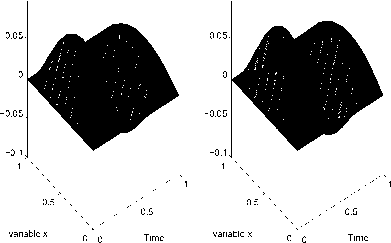
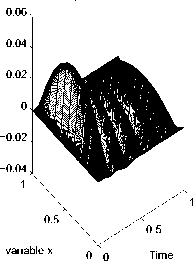
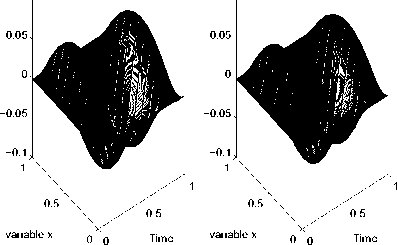
Величина погрешности, при которой проводились расчеты, обозначена 5. Двумерные поверхности, имеющие обозначение «Exact Solution», соответствуют решениям U k прямой задачи (4), (5), построенным для тестовых функций. Поверхности, соответствующие решению u^(x,t), полученному с использованием функции fj, обозначены как «Verification».

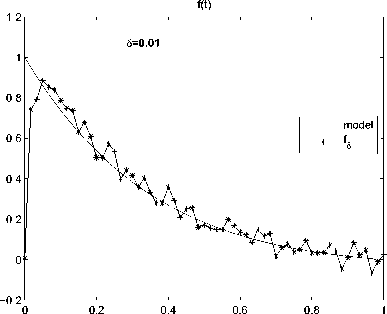
Рис. 2. Результаты численного решения задачи (1)-(3) для функции f2(t)

Exact Solution

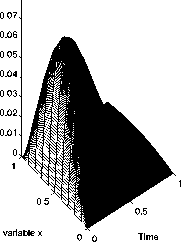
Verification

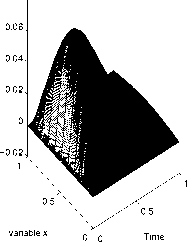
На основании полученных результатов эксперимента можно сделать следующие выводы. Предложенный метод решения задачи идентификации функции источника позволяет получать регуляризованные решения с удовлетворительной точностью. При этом уровень погрешности исходных данных оказывают наиболее существенное влияние на величину погрешности приближенного решения f¹. Влияние значений N и а на величину уклонения f

Таблица 3

Экспериментальная погрешность Af1 для функций fi

N	а = 10-3	а = 10-4	а = 10-5	а = 10-6	а = 10-7	а = 10-8
3	0,0557	0,0536	0,0510	0,0524	0,0529	0,0538
4	0,0548	0,0512	0,0462	0,0474	0,0480	0,0491
5	0,0425	0,0386	0,0367	0,0381	0,0402	0,0408
6	0,0478	0,0433	0,0424	0,0442	0,0455	0,0461
7	0,0521	0,0508	0,0515	0,0518	0,0522	0,0524

Таблица 4

Экспериментальная погрешность Af2 для функций /2

N	а = 10-3	а = 10-4	а = 10-5	а = 10-6	а = 10-7	а = 10-8
3	0,8210	0,8115	0,7934	0,8024	0,8212	0,8234
4	0,8181	0,8023	0,7732	0,7874	0,8034	0,8177
5	0,8052	0,7756	0,7471	0,7618	0,7945	0,8067
6	0,8137	0,7893	0,7723	0,7856	0,8076	0,8111
7	0,8164	0,8005	0,7802	0,7912	0,8085	0,8123

Таблица 5

Экспериментальная погрешность Af3 для функций /з

N	а = 10-3	а = 10-4	а = 10-5	а = 10-6	а = 10-7	а = 10-8
3	0,0490	0,0478	0,0463	0,0468	0,0472	0,0478
4	0,0474	0,0467	0,0437	0,0445	0,0448	0,0451
5	0,0453	0,0438	0,0412	0,0418	0,0421	0,0423
6	0,0464	0,0452	0,0441	0,0445	0,0451	0,0452
7	0,0470	0,0462	0,0450	0,0458	0,0462	0,0465

Таблица 6

Экспериментальная погрешность Af4 для функций f4

N	а = 10-3	а = 10-4	а = 10-5	а = 10-6	а = 10-7	а = 10-8
3	0,0549	0,0543	0,0538	0,0542	0,0544	0,0546
4	0,0545	0,0539	0,0531	0,0535	0,0540	0,0542
5	0,0536	0,0529	0,0522	0,0533	0,0537	0,0539
6	0,0542	0,0536	0,0531	0,0535	0,0539	0,0542
7	0,0547	0,0542	0,0536	0,0540	0,0545	0,0549

Таблица 7

Экспериментальная погрешность Af5 для функций f5

N	а = 10-3	а = 10-4	а = 10-5	а = 10-6	а = 10-7	а = 10-8
3	0,1157	0,1154	0,1141	0,1143	0,1145	0,1146
4	0,1153	0,1115	0,1132	0,1134	0,1137	0,1141
5	0,1147	0,1143	0,1112	0,1118	0,1122	0,1127
6	0,1149	0,1146	0,1127	0,1129	0,1131	0,1133
7	0,1151	0,1147	0,1135	0,1136	0,1136	0,1137

Таблица 8

Экспериментальная погрешность Af6 для функций fg

N	а = 10-3	а = 10-4	а = 10-5	а = 10-6	а = 10-7	а = 10-8
3	0,0842	0,0838	0,0836	0,0839	0,0841	0,0840
4	0,0834	0,0832	0,0826	0,0830	0,0837	0,0839
5	0,0828	0,0817	0,0811	0,0819	0,0825	0,0827
6	0,0830	0,0825	0,0819	0,0827	0,0828	0,0829
7	0,0832	0,0831	0,0827	0,0829	0,0830	0,0831

f(t)

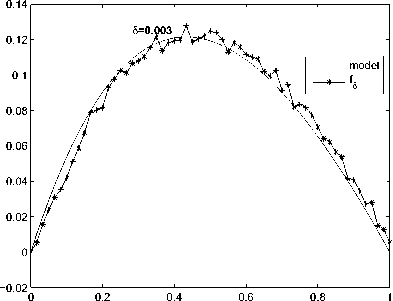
Рис. 3. Результаты численного решения задачи (1)-(3) для функции fa(t)

Exact Solution

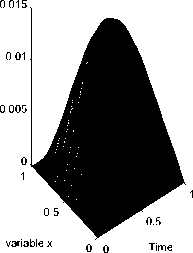
Verification

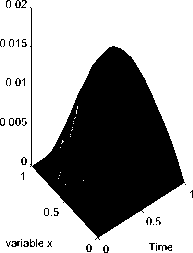
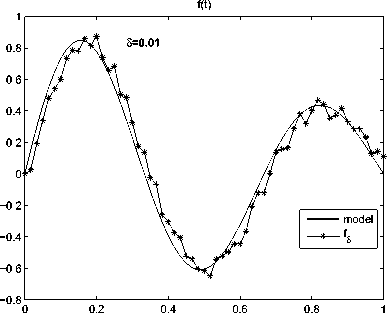
Рис. 4. Результаты численного решения задачи (1)-(3) для функции f4(t)

Exact Solution

Verification

0.1

f(t)

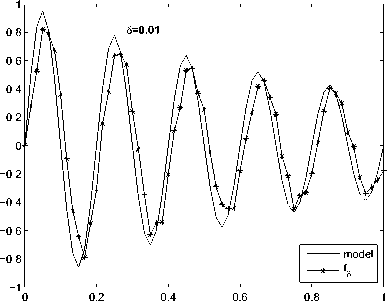
Рис. 5. Результаты численного решения задачи (1)-(3) для функции fa(t)

Exact Solution

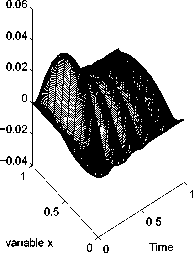
Verification

от f k ^ПР^И рассматриваемом подходе к моделированию возмущенных данных имеет гораздо меньший эффект, что позволяет ограничиваться небольшими значениями этих параметров при проведении расчетов, основанных на результатах реальных измерений.

Заключение

В статье рассмотрена обратная задача идентификации функции источника для параболического уравнения. С помощью применения прямого и обратного перобразований Л апла-

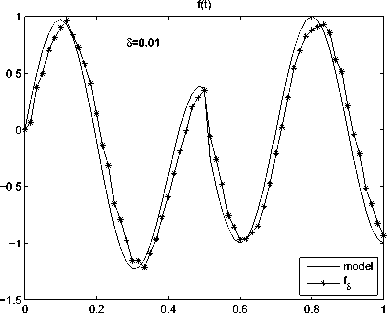
Рис. 6. Результаты численного решения задачи (1)-(3) для функции fa(t)

Exact Solution

Verification

0.1

0.1

са эта задача сводится к решению уравнения Вольтерра первого рода, характеризующее прямую зависимость неизвестной функции источника от известных граничных условий. Такой подход позволил исключить неустойчивую процедуру численного обращения преобразования Лапласа из вычислительной схемы. В статье предложен численный метод решения полученного интегрального уравнения, основанный на применении регуляризующего алгоритма с апостериорным выбором параметров регуляризации и послуживший основой для проведения вычислительного эксперимента. Результаты эксперимента свидетельствуют об устойчивости регуляризованных решений и достаточной эффективности предложенного подхода к решению задачи идентификации функции источника. Для более строгого исследования влияния параметра N на точность решений требуется провести дополнительные исследования, в которых возмушения в правой части (13) задаются специальным образом. Результаты данного исследования могут быть использованы при решении прикладных задач, возникающих, например, в металлургии, машиностроении, а также при исследовании различных диффузионных прцессов.

С целью уточнения оценки погрешности решений, полученных при использовании этого подхода, и улучшения сходимости построенных решений в дальнейшем планируется рассмотреть численное решение уравнения такого типа с помощью подходов, основанных на устойчивых разностных методах, где в качестве параметра регуляризации выступает шаг сетки по аналогии с результатами, представленными в работах [12], [14].