Метод С. К. Годунова для многоскоростной модели гетерогенной среды

Ранние модели гетерогенных сред не являлись гиперболическими, что приводило при их использовании к появлению различного рода, нефизичных эффектов, связанных, например, с наличием волн, распространяющихся с бесконечно большими скоростями. Кроме того, для этих моделей, описывающих течение гетерогенных сред, задача. Коши не всегда, оказывалась корректной, что затрудняло применение численных методов [1]. Поэтому дальнейшее развитие получили гиперболические модели гетерогенных сред. Обзор наиболее часто используемых гиперболических моделей имеется в [2].

В настоящей работе используется гиперболическая модель из работы [3], в которой введено в рассмотрение такое состояние среды как смесь в целом, характеризуемая осреднен-ными значениями величин, уравнения для которых совпадают с газодинамическими. К этим соотношениям добавляются уравнения, выражающие законы сохранения, но только для тех компонентов смеси, в которых локальные скорости перемещения возмущений не превышают скорость движения волны в смеси в целом. При этом считалось, что остальные волны поглощаются средой, формируя волну в смеси. Давление полагалось общим для всех фракций смеси. Для газожидкостных смесей модель с газодинамическим ядром из [3] описывает « пузырьковое » течение, и оно полностью соответствует наблюдаемому в экспериментах (см. [2]).

Метод С.К. Годунова. (МГ) [4], широко используемый для решения газодинамических задач, предназначен для численного интегрирования гиперболических систем уравнений, записанных в дивергентной форме. Применение оригинального МГ для интегрирования уравнений многоскоростной гетерогенной среды невозможно, поскольку система, определяющих уравнений модели [3] не является полностью дивергентной. В представленной работе описан модифицированный МГ, позволяющий численно решить систему уравнений модели

В.С. Суров, И.В. Березанский гетерогенной среды с газодинамическим ядром из [3] недивергентного вида. Отметим, что ранее МГ успешно использовался для расчета течений, описываемых различными моделями гетерогенных сред в рамках односкоростного приближения. В частности, в работе [5] МГ с точным римановским решателем из [6] использовался при исследовании ударно-волновых процессов во вспененных жидкостях в рамках условно гиперболической модели. В работе [7] описан модифицированный МГ, предназначенный для интегрирования уравнений гиперболической модели односкоростной гетерогенной среды из [8]. Для этой модели среды точный решатель Римана, используемый в алгоритме метода, представлен в работе [9], а приближенный – в [10].

Поведение сжимаемых фракций для определенности будем описывать с помощью двучленного уравнения состояния

E i =

P - c *i (P 0 — P *i) = b i + pB i P^{0 (}Y i ^- 1)           P 0

- d i ,

где E - удельная внутренняя энергия, р 0 - истинная плотность i -й фракции, B i = 1/(Y i — 1) , d i = c^ i B i , b i = d i P * i ( Y i , P *i , c *i — константы, индивидуализирующие i -ю фракцию). В частности, для воды - y = 5.59, c * = 1500 м/с, р* = 1000 кг/м ³ .

При рассмотрении алгоритма МГ ограничимся одномерным приближением. Используемый подход непосредственно обобщается на многомерный случай.

1.    Модель гетерогенной среды

Система уравнений n -компонентной смеси с первыми m сжимаемыми фракциями, описывающая одномерное течение многоскоростной гетерогенной среды из [3], включает в себя уравнения законов сохранения массы, импульса и энергии для смеси в целом др + dpu = 0 ∂t ∂x

дри   д (р + ри²) _

∂t ∂x

∂p ∂p

8t + "ax

-

c 2 д1+ ulr^ = °- ∂t ∂x

где c - скорость перемещения волны в смеси в целом, e = E + 2 и ² - удельная полная энергия смеси, p – давление, u – скорость смеси, ρ – плотность смеси.

Для сжимаемых фракций имеем 3( m – 1) законов сохранения:

da i p ⁰ la i p 0 U i         da i p^U i ^da i p + P 0 ^u 2)

"ат; ⁺ ^x? = ⁰' ""8^ ⁺----lx----= ⁿi^(u - ^{u i )}'          (3)

∂α i ρ ⁰ e i    ∂α i ρ ⁰ e i u i ∂α i pu i

—57--1--5--1--5  = n i U i (u - Ui)' i = 1'...,m - 1'

∂t        ∂x ∂x где αi – объемная доля i-й фракции.

Для несжимаемых компонентов справедливы 2( n – m ) выражений

∂α j    ∂α j u j

∂t ∂x

= 0 '

la j U j ^da j (^u j ^{+ pp} j)    n j (u — U j )

∂t           ∂x             ρ _j ⁰

j = m + 1,..., n,

представляющие собой законы сохранения массы и импульса.

При записи уравнений (3) для определенности полагалось, что скорость возмущений в m -й фракции превосходит с , поэтому законы сохранения для этой составляющей опущены. При расчете сил сопротивления предполагалось, что они пропорциональны разнице скоростей смеси в целом и отдельного компонента. При вычислении скорости волны в смеси в

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ целом использовалась формула обобщенно-равновесной модели, которая в случае применения двучленного уравнения состояния (1) принимает вид m-1

Bm + £ i=1

a i (b m B i — b i B m )

b i + pB i

^-1                      m - 1

b m + P 1 + B m -£

^a i ^{( b} im + pB im )

b i + pB i

,

где b im = b i — b _m , B im = B i — B m . Скорость c из выражения (5) близка к рассчитанной по аппроксимирующей экспериментальные данные формуле Вуда (6) [11].

n

• ¹    = ^a k

• 2              0 2 ^.

ρc     _{k - 1} ρ _k c _k

k - 1

Перепишем систему уравнений (2) – (4) в квазилинейной форме как где

∂ρ ∂ρ ∂u dt + UdX + PdX = 0,

∂α i      ∂α i

"dt ^{+ U i} dX ⁺

du + du + 1 dp 0 ∂ρ _i ⁰      ∂ρ _i ⁰       ∂u ^ρ ∂p

“;x~ ^{+ u} i "XX--Hi xx-- K i XX^-

∂t     ∂x∂x ∂x dui     dui    1 dpda

∂t   ui ∂x   ρi0 ∂x

-

-

-

∂p ∂p    2 ∂u at + udX + pc dX = 0;

L dr = o.

∂x

η i

α i ρ _i ⁰

(u — U i ) ,

a^Hj du + a i K i dp ₊    1 LA du i

ρ _i ⁰ ∂x ρ _i ⁰ ∂x ⁱ ρ _i ⁰ ∂x dm ₊ .dm ₊ 1 dp ₊ G.da j = n j ∂t ^j ∂x   ρ _j ⁰ ∂x     ^j ∂x    α j ρ _j ⁰

∂α j -m + uj

∂t

= 0, i = 1,... ,m — 1;

(u — U j ) ,

d,+ - j ^d =0, ∂x ∂x

j = m + 1,..., n,

H = pc^p^Ei i   -iGi + p^Fi,

F i =

K i =

( u — u i ) p _i ⁰ E i

∂ε i ∂ρ _i ⁰

-

^a i G i ^{+ p} 0 F i

L i = —

α i ρ _i ⁰ G i

p = ( p 0)2

-

b i ^{+ p (1 +} B i )

( P 0)²        ’

^a i G i ⁺ P 0 F i

∂ε

E i =

∂p

G i = A- α i ρ _i ⁰

B i _{ρ i} 0 ^,

Систему (7) можно представить в векторном виде как dU + YdU = S

∂t ∂x , где

^U = (p,u,p, [ p ⁰ ,u i ,^a i] ^m _:1 ¹ , [u j ^,- j ] n ₌ m ₊ i

S = 0 , 0 , 0 , 0 ,

П (u — u i ) α i ρ _i ⁰

m - 1

, 0

i =1

n j ^{( u —} u j )

α j ρ _j ⁰

, 0

,

В.С. Суров, И.В. Березанский а матрица Y примет вид

0 u       ρ 0 u	0          0     0     0     ...     0         0         0        0        0      ...    0     0 1 0     0     0     ...     0         0         0        0        0      ...    0     0
0         ρc 2 B B 0       - H 1	ρ u          0     0     0     ...     0         0         0        0        0      ...    0     0 - K 1         u 1    - L 1     0     . . .      0         0          0         0         0       . . .    0     0 C
00	1              0       u 1      G 1     . . .       0           0            0          0          0        . . .     0      0 ρ 01
α 1 H 1 v          0 ρ 01	α K           c 2 1 1         0       1 u ...      0         0          0         0         0       ...    0     0 ρ 0 1                  G 1       1
B 0    - H m-1	- K m-1       0     0     0    . . .  u m-1   - L m-1      0       0       0      . . .   0    0 C
00	ρ 0 1 -1         0      0      0     . . .      0        u m-1     G m-1       0         0       . . .    0     0 C
α m-1 H m-1 ρ 0 m-1	α m- 0 1 K m- 1    0    0     0    ...    0       c 2 m- 1     u m-1      0       0      ...   0    0 ρ m-1                                  G m- 1 1
00	0           0    0     0    ...    0        0        0      u m+1   G m+1   ...   0    0
B0             0	m 0 +1         0     0     0     . . .     0         0         0      α m+1 u m+1 . . . 0     0 C
B 0             0 00	0     0     0     ...     0         0         0        0        0      ...   u n    G n C ρ 0 n 0         0     0     0    ...     0        0        0       0       0      ...  α n    u n

Штрихом отмечен оператор транспонирования.

Матрица Y имеет только действительные собственные значения, которые равны u ± c, u,   u1 ± c1 ,   u1 ,   . . . ,   um-1 ± cm-1 ,   um-1 ,   um+1 ± cm+1 ,   . . . ,   un ± cn, где pFi                               p ci \               Qp , i 1, . * * , m 1; cj 4 / 0 , j m + 1, * * * ,n*

у ^a i G i + p 0 F i                           у p 0

Кроме того, собственные векторы, соответствующие собственным значениям, линейно независимы, поэтому система уравнений модели относится к гиперболическому типу.

2.    Метод Годунова для недивергентных систем

Систему (2) – (4) перепишем в векторной квазидивергентной форме dW+dF+p - p) dG=s, ∂t ∂x           ∂x

где

W = (p,pu,p, [ a i p ⁰ , a i p ⁰ U i , a i p ⁰ e i ] i=₁ ¹ , [a j- ,a j u j ] n=_m+1) ,

F = ^pnpp ⁺ pu 2 ,p^u, [aip ⁰ u i , ^a i (^ p ⁺ p ^{0 u} 2 ) , u i ^{( a} i p ⁺ p i ^e i ) ] m=₁ ¹ , [ ^a j u j , ^a j (u ^{2 +} pp ° )] n_=m+1 G =(0,0,u, 0, ***, 0) ’ ,

,

′

S = 0, 0, 0, [0, n i (u - u i ) , n i u i (u

m -1

u i ^)] i=1 , ⁰,

n nj (u - uj)

ρ _j ⁰

j = m +1

.

Переходя от дифференциальных соотношений в (9) к конечно-разностным, получим следующее явное выражение, связывающее искомые параметры на новом временном слое t +At

(с индексами вверху) с соответствующими значениями на предыдущем слое t (с индексами

внизу):

W ^k - W k   ^F k +1 / 2 ^{- F} k -1 / 2             ^G k +1 / 2 ^{- G} k -1 / 2

⁺-----AX-----⁺<^{pc -} p к -----AX-----

= S k ,

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ где Fk±i/2= RuU, P + RU2, PU,

{AR ^ Ui, A i ( P + R^ , A i U i ( P + R 0 E i )] m=₁ ¹

G k±i/2 =(0,0,U, 0,..., 0) k±i/2 .

′

JA j U j .A j j + R 0')l     )

^j     j=m+1 _{k ± 1/2}

,

Используемые в (10) обозначения соответствуют принятым в [4]: узлы конечноразностной сетки имеют целые индексы, а грани ячеек – полуцелые. ≪ Большие ≫ величины, которые входят в выражения (10) ( P – давление; U , U i , U j – скорости, R – плотность смеси; R _i ⁰ и E i –плотность и удельная полная энергия i -й составляющей смеси; A i , A j – объемные доли), относящиеся к граням смежных ячеек, определяются из решения соответствующих задач Римана, алгоритм для расчета которых приведен ниже.

Другой способ интегрирования недивергентной системы (2) – (4) связан, как и в предыдущем случае, с выделением уравнений, приводящихся к дивергентному виду, для которых выписываются явные выражения, связывающие искомые параметры на новом временном слое t + At (с индексами вверху) с соответствующими значениями на предыдущем слое t (с индексами внизу):

^{p k} — ^p k ⁺ [ ^{(R U} ) k-1/2 ^{— ( RU} ) k+1/2 ] AX’

^{(pu) — (pu) k +} [( ^{P + RU} ) k-i/2 ^— ( ^{P + RU} ^+1/2 ] A X ’

( ^{a i P} 0 ) ^— ( ^{a i p} 0 ) k ⁺ [( ^{A i R} 0 ^U ) k-i/2 ^— ( A i R i’ U ) k₊i/2 ] AX^;

( ^a i ^p 0 ^u i ) ^— ( ^a i ^p 0 ^u i ) _k ⁺ |( ^A i P ^{+ A} i ^R 0 ^U i ² ) _{k - 1}/₂ ^— ( ^A i ^{P +} A i RiUi') k +1 / 2 ^ AX⁺ + [n i (u — U i )] _k At’

( ^a i ^p 0 ^{e i} ) ^— ( ^a i ^p 0 ^{e i} ) k ⁺ | [( ^R 0 ^{E i +} P i ) ^{A i U i} ] k-1/2 ^— [( ^R 0 ^{E i +} P i ) ^{A i U i} ] k +1 / 2 ^ AX⁺

+ [n i U i (u — U i )] _k At’      i — 1,...,m — 1;

(a j ) k — (a j ) k +[(A j U j )

k-1/2 ^{(A j U j} ) k+1/2 ] A_X’

^(a j u j ^{) k — (a} j u j ) k ⁺ *

[^Aj (U ^{2 +} jlk-1/2 — [^А' (U ^{2 +} 3l

At

AX⁺ k+1/2

+

n j ^{( u —} u j ) ^ρ j ⁰

_k At,

j — m + 1,..., n.

Используемые в (11) обозначения соответствуют принятым в [4].

Для вычисления оставшейся неизвестной переменной p на новом временном слое запишем в конечно-разностном виде третье уравнение (2), используя противопоточную схему, как pk - pk - pk+1 - pk + pk - pk-1

—--+ Ufc ---X-- + u+---X----

At ^k AX ^k AX

2 c _k

(

ρ ^k

- ρ _k

At

^ρ k+1 ^{- ρ} k

+ Ufc k   AX

^ρ k ^{- ρ} k-1

+ u + ---X---- k    _{A X}

— 0,

где

В.С. Суров, И.В. Березанский

“ + = ^^(u k ⁺ | u k I ) ’ “k = ^^(u k - ^{| u} k I ) •

Из уравнения (12) вычисляется давление p ^k , что завершает вычислительный цикл. Отметим, что ранее подобный подход показал свою эффективность в расчетах течений односкоростной гетерогенной среды (см. [7]).

3.    Линеаризованный римановский решатель

Задача Римана для гетерогенной среды формулируется следующим образом. Пусть имеются две однородные многокомпонентные массы среды, состоящие из n L и n R составляющих каждая, расположенные в начальный момент t = 0 соответственно « слева » от плоскости x = 0 и « справа » от нее. Необходимо рассчитать течение, возникающее при t >  0 . « Точ-ный ≫ решатель задачи Римана для модели из [3] приведен в [12], применение которого требует значительных временных затрат. Существует ряд ≪ быстрых ≫ способов приближенного решения задачи Римана для сред, описываемых системами гиперболических уравнений. Это решатели Роя, Хартена – Лакса – ван Лира (HLL, HLLC), Лакса – Фридрихса, Русанова и др. [13, 14], предназначенные в основном для дивергентных систем. В этом разделе описан алгоритм линеаризованного римановского решателя (LRR) [15] для модели среды с газодинамическим ядром.

При описании римановского решателя для определенности ограничимся газожидкостной смесью, состоящей из двух сжимаемых сред – газа, параметры которого отмечены индексом g, и жидкости (с индексом l). В этом случае система дифференциальных уравнений (2) – (4) принимает вид где

d^p +Л+pdu = 0, ∂t ∂x ∂x

du du 1 dp ∂t u ∂x ρ ∂x

∂p ∂p

= ^0, at ⁺ “dx

-

∂ρl0     ∂ρl0      ∂u dt + Ul dx l Эх txx

;dt^{+ U l} dx ⁺ p 0 dx^{+ G l} ^x = ap ^{0 ( u - U l ) s} S’

-

-

_K ∂p l _∂x

-

η l

∂u

L l^ = 0, ∂x

c2 X'+ “Ir^ =0, ∂t ∂x

∂αl     ∂αl d + ul dx +

α l H l ∂u

_{ρ l} 0 _∂x

+

α l K l ∂p

_{ρ l} 0 _∂x

α l ρ _l

+ a _l 1 +

L l ∂u l p¹⁰) dx = ’

H l =

ρc ² ρ _l ⁰ E l

a i G l + p 0 F i ,

K l

(u - “ l ) p ⁰ E l a l G l + p ⁰ F l ’

L l

-

α l ρ _l ⁰ G l a l G l + p ⁰ F l ’

B l

E l = ^_0^, ρ _l ⁰

F i =

-

b l + P (1 + B l )

ρ _l 0 2

p

’    G l           A ’

α l ρ _l ⁰

cl=v

pFl al Gl + P^Fl

G g =

p

α g ρ ⁰ _g ^,

F g =

-

c = Уp ^-1 [ s , +

b g ^{+ p (1 +} B g )

( P 0 ) 2        ’ c g

=

pF g

^a g ^G g ^{+ р}^ д

a i (b g B i

-

b l B g

b l + pB l b lg = b l

)] I

b _g + p 1 + B _g

-

a l (b lg + pB lg bi + pB l

) ,

-

b g ,    B lg = B l — B g .

Поскольку скорость перемещения возмущений c _g превосходит скорость движения волны в смеси в целом, поэтому уравнения для газовой фракции не включены в общую систему уравнений.

Формула линеаризованного римановского решателя, с использованием которого вычисляются параметры смеси на контактной границе ( U C ) по известным значениям параметров

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ среды слева (UL) и справа (UR) от нее, имеет вид (см. [15]):

U C

1 ⁶

= U - 2 52 a k sign (^X k ) R k • k=1

В (14) введены обозначения

U C

ρ

u

ρ

u

ρ

u

p

P l

U i

α l _C

U = 2 ( U l + U r ) , U l

^p ρ l

U l

α l   _L

p

P l

U l α l

R

Правые собственные векторы R k системы (13), соответствующие корням характеристического уравнения A i = u , A 2 = u i , А з = u i — c i , A 4 = u i + c i , A 5 = u — c , А б = u +c , имеют вид

R 1 =

R 4 =

V

V

-

-

\

/

c l

L

c _l

L l G l

,

/

R 2

,

V

R 5 =

V

\

/

,

-

ρ

c

- ρc

Q 1

Q 2

Q 3

R 3

/

,

0 0

0 L l c l 1

c l ^- G l

R 6 =

ρ _c

Pc

Q 4

Q 5

Q 6

где pl (Hl — PcKl) (u — c — ul)2 — c2 + Ll [alGlHl + Pc (ul — u + c — alGlKl)]

Qi =

P 0 (u — c — u l ) [ (u — c) ² + u l ² — c l ² — 2u l (u — c) ]

Q = ^a l ^G l ^H l ⁺ Pc ^{( u} l — ^{u +} c — ^a l ^G l ^K l ) Q = ^a l ^G l ^{( u} — ^u l — ^{c) (H} l — ^PcK1 ) — ^Pc cl ²     P 0 [ (u — c) ² + u l ² — c l ² — 2u l (u — c) ] ’      ³     P 0 G l [ (u — c) ² + u l ² — c l ² — 2u i (u — c) ] ’

P l ⁽ H l ⁺ PcK l ) ^{(u +} c ^{— u} l ^{) — c} 2 ⁺ L l ^{[ a} l G l H l ⁺ Pc ^{( u +} c ^{— u} l ^{— a} l G l K l ^)]

Qa =

P 0 (u + c — u l ) [ (u + c) ² + u l ² — c l ² — 2u l (u + c) ]

Q = ^a l ^G l ^H l ⁺ Pc ^{( u — u} l ⁺ c ^{+ a} l ^G l ^K l ) Q = ^a l ^G l ^{( u — u} l ^{+ c) (H} l ^{+ P}c^K l ) ^{+ P}cci

• ⁵     P 0 [ (u + c) ² + u l ² — c l ² — 2u l (u + c) ] ’      6     P 0 G l [ (u + c) ² + u l ² — c l ² — 2u i (u + c) ]

В.С. Суров, И.В. Березанский

Значения констант a 1 , ... , a 6 , которые входят в (14), определяются из выражений a i —Ap — ^Ap, c ²

0 LlGl a2—Apl +--2~ l        cl2

а з — 2 (Au i —

Aa i —

^Ap [q4 - Q i +

2Pc

L l G l

2 c _l

^(Q 6 ^— Q 3 )

-

Au

""2"" Q4 ^{+ Q} 1 ⁺

L^ (Q 6 + Q 3 ) , c _l ²

G l

—A a i c l

) +^^ 2 — Q 5 +

7    4Pc L

— ^(Q 6 ^{— Q} 3 ) j    4" ^ Q 2 ⁺ Q 5

-

^(Q 6 ^{+ Q} 3 ) j , c l

a ^{4 —}L  ^v

l

-

G 1 л     Ap

-^Aai ⁺ -— Q 5

c l          2Pc

-

Q 2 +^(Q 6 ^{— Q} 3 ) c l

Au

■ 2

Q 2 ⁺ Q 5 +^(Q 6 ^{+ Q} 3 ) 1, c l

где

a 5 2 ^Au

-

—Ap) , ρc

a6 —

1 ^Au + — Ap^ , 2 V Pc 7

AP— P _R — P L ,  Au—u R

AP 0 — ( p 0 ) r

-

u L ,  Ap—p R — p L ,

Au i — (u i ) R

-

^{( u}ik,

-

(P0)L,   ^Aa l ^{— (a} l )

R

-

^{( a} i ) L •

≪ Большие ≫ величины, входящие в расчетные формулы (10) – (11), вычисляются из соотношений:

(R,U,P,U i ,R i ,A i ) k+i/2 —

ρ, u, p, u l , ρ _l ⁰ , α l _k , ρ, u, p, u l , ρ _l ⁰ , α l _k+1 , ρ, u, p, u l , ρ _l ⁰ , α l _C ,

(u — c) c > 0;

(u + c) c < 0;

(u — c) c <  0, (u + c) c >  0

4.    Результаты численного моделирования

В качестве примера применения описанных выше алгоритмов МГ рассчитана задача об отражении ударной волны в газожидкостной смеси от абсолютно жесткой неподвижной стенки. Константы уравнения состояния уравнения (1) для жидкой фракции следующие: p *l — 200 кг/м ³ , Y *i — 5,59, c *i — 1500 м/с. Соответствующие константы уравнения (1) для газа: p *g — 1,19 кг/м ³ , Y *g — 1,14, c *g — 0. Коэффициент П 1 принимался равным нулю. Параметры смеси до распада следующие: слева от диафрагмы ( х <  0) - p o l — 0,15 МПа, u o l — ui o l — 0, a i o L — 0,05, p 0_0L — p *i , p g_0L — p *g ; справа от нее ( x >  0) - p o r — 0,1 МПа, u o r — u i 0 R — 0, a i o R — 0,05, p 00R — p *i , P^ o r — p *_g . В момент времени t = 0 диафрагма мгновенно удаляется, при этом реализуется режим течения с волной разрежения, перемещающейся влево и ударным скачком, движущимся вправо.

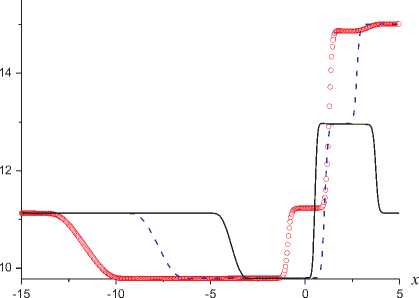
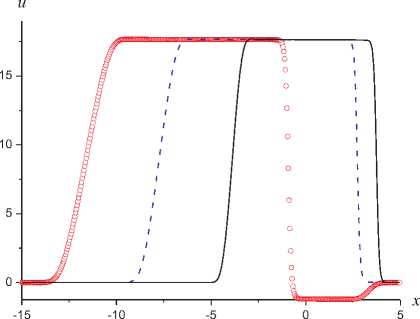
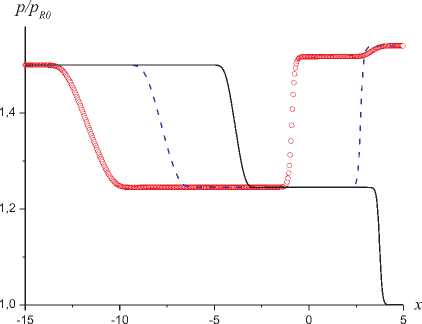
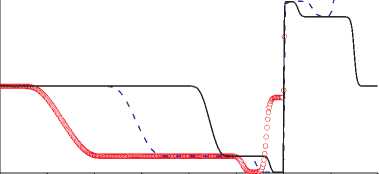
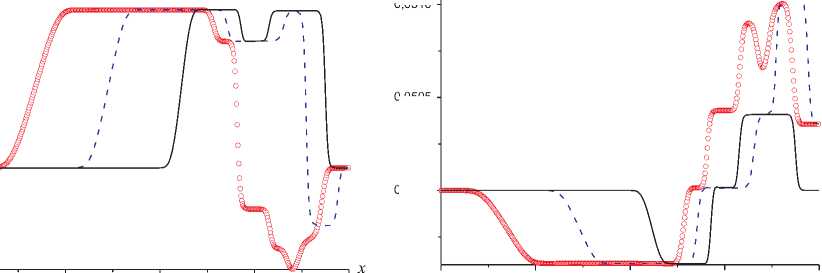
На рисунке представлены результаты расчетов, полученные к моментам времени t = 0,03, 0,06 и 0,09 с. Данные этого рисунка иллюстрируют возникновение ≪ вторичных ≫ волн при распаде начального разрыва (сплошные кривые), формирование отраженной ≪ вторич-ной ≫ волны, возникшей вследствие отражения УВ от преграды (пунктирные кривые), процесс взаимодействия движущейся к преграде и отраженной ≪ вторичных ≫ волн (кружочки). Отметим, что описанная картина образования и взаимодействия ≪ вторичных ≫ волн происходит на фоне неизменного уровня давления. Под ≪ вторичными ≫ волнами подразумеваются волны, характеризуемые измененными значениями объемных долей отдельных компонентов в смеси и их локальных скоростей при неизменном профиле давления.

Заключение

Описан модифицированный метод С.К. Годунова, предназначенный для интегрирования уравнений многоскоростной многокомпонентной смеси недивергентного вида. При расчете

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

р

р l

200,01

200,00

199,99

ul

200,02

-10

-5

x

-15

0,0510

^ l

1,0

0,5

0,0

-0,5

0,0505

0,0500

-15

-10

-5

-10

-5

x

-15

Зависимости p(x) , u(x) , p(x)/p R0 , P 0 (x) , u l (x) , a l (x) к моментам времени t = 0,03 (сплошные), 0,06 (пунктирные), 0,09 с (кружочки), полученные с использованием формул (10)

задач распада произвольного разрыва использован линеаризованный римановский решатель. Рассмотренный метод расчета непосредственно распространяется на задачи с несколькими пространственными переменными. Расчеты рассмотренной задачи, выполненные по формулам (11) – (12) с точностью до графического представления совпадают с данными, полученными с использованием выражений (10) представленными на рисунке.

В.С. Суров, И.В. Березанский