Метод сопряжённого уравнения в задаче об определении источника диффузии

Значительная часть теоретических расчетов наблюдаемых в экспериментах величин производится с целью проверки тех или иных предположений о характере среды или параметрах физической модели, описывающей изучаемое явление (процесс). Вычисления наблюдаемых физических величин принято называть прямой задачей . Определение же количественных характеристик модели по экспериментально наблюдаемым величинам на основе теоретических расчетов принято называть обратной задачей.

Как и в классе прямых задач, методы решения задач обратного типа разделяются на две группы: аналитические и численные. К первой относятся построение функционально-инвариантных решений гиперболических уравнений, аналитические представления решений и коэффициентов параболических уравнений, представление решения и коэффициента уравнения Штурма-Лиувилля с применением в обратных задачах теории рассеяния, построение гармонических и других потенциалов для вычисления решений (скорости) и коэффициентов (давления) системы уравнений газовой динамики и др. [1-3].

Вторую группу составляет большая коллекция численных методов (см. монографии [4-7] и др.). Особую роль играют задачи, в которых определению подлежат положения и свойства удалённых (во времени и пространстве) источников. Назовём их обратными задачами первого рода , отнеся ко второму роду задачи по извлечению информации о коэффициентах диффузионных уравнений. Примеры обратных задач первого рода рассматриваются в работах [6-14]. В частности, в

[9-10] развивается метод решения обратной задачи диффузионного типа, основанный на использовании прямого и обратного преобразований Лапласа, что позволяет свести исходную задачу к решению интегрального уравнения Вольтерры первого рода, характеризующего прямую зависимость искомой функции источника от известных граничных условий.

Однако в большинстве практически интересных случаев решение прямой задачи не выражается в аналитическом виде, не говоря уж об обратной задаче. На деле это сводится к параметризации физической модели изучаемого процесса с дальнейшим определением количественных значений этих параметров на основе лучшего совпадения результатов теоретических расчетов с экспериментально измеренными значениями. При этом сама процедура параметризации физической модели зачастую неоднозначна, а вводимые параметры требуют дополнительного физического толкования.

Подробное описание постановки различного типа обратных задач можно найти в работах [6, 7]. В настоящей работе рассматривается частный случай обратной задачи по определению функции источника, основанный на двойственном представлении показаний детектора с использованием функции ценности [15, 16] и в этом смысле являющийся продолжением идей, сформулированных в наших ранних работах [17, 18].

Описание метода

Уравнение теплопроводности (диффузии), как и другие уравнения переноса, могут быть представлены в операторной форме

L Ф ( u ) = S ( и ),                                           (1)

где и - набор фазовых координат, например, для одномерного уравнения диффузии и = { t, x }. Наличие известного решения Ф( и ) превращает определение источника S ( и ) в прямую задачу о вычислении L Ф( и ), и особых проблем не возникает. Однако в реальном физическом эксперименте измеряются не значения функции Ф( и ), а некоторый функционал от неё, представляющий показание прибора (детектора). Ограничившись линейным представлением, запишем его в виде скалярного произведения

J = J du Ф ( и ) D ( и ) = ( Ф , D ).                                 (2)

Введя в функцию чувствительности детектора D ( и ) совокупность характеризующих его параметров а , выразим этот функционал через решение соответствующего сопряженного уравнения (функцию ценности):

L ⁺Ф⁺ ( и , а ) = D ( и , а ),                                     (3)

оператор L + в котором удовлетворяет соотношению Лагранжа:

(Ф⁺, L Ф) = (Ф, L ⁺ Ф⁺).

Согласно принципу двойственности показания такого детектора могут быть выражены также через функцию ценности:

J ( а ) = J du Ф⁺ ( и , а ) S ( и ) = ( Ф⁺ , S ).                             (4)

Таким образом, использование двойственного представления функционала естественным образом сводит задачу параметрического определения функции источника (в чем и состоит специфика данной работы) к решению интегрального уравнения первого рода. Будет это уравнение Вольтерры или Фредгольма, зависит от свойств оператора переноса L и граничных условий задачи. Заметим также, что отмена правой части уравнения (1) и использование вместо неё начального условия

Ф (0, x ) = g ( x )                                         (5)

эквивалентно задаче (1) с функцией источника:

S ( t , x ) = J ( t ) g ( x ), содержащей дельта-функцию, отвечающую мгновенному (импульсному) характеру источника.

Если функцию чувствительности детектора выбрать в виде

D ( t , x ) = 5 ( t - t o ) £ ( x - x 0 ),                                     (6)

Математика

(заметим, здесь t 0 , x 0 представляют совокупность α ), то решением уравнения (3) будет функция Грина, через которую могут быть выражены решения, соответствующие другим функциям чувствительности, то есть другим функционалам (2).

Рассмотрим модельную задачу для одномерной диффузии в неограниченном пространстве с различными точечными источниками:

S ( t , x ) = φ ( t ) δ ( x ).

Дополнительным как для уравнения (1), так и для уравнения (3) в этом случае будет граничное условие – равенство нулю на бесконечности искомых функций.

В случае постоянного коэффициента диффузии a ² уравнение (3) имеет вид:

-

∂Φ+ ∂t

-

a ²

∂2Φ+

∂ x ²

= δ ( t - t ₀) δ ( x - x ₀).

Данное уравнение отличается от классического «прямого» уравнения только знаком перед производной по времени. Путем замены переменных оно легко сводится к классическому уравнению диффузии (теплопроводности), для которого решение известно:

Φ⁺ ( t , x , t ₀, x ₀) =

exp 2 a π ( t 0 - t )

-

( x - x 0 ) 2 ^ ⁴ a 2 ( ‘ 0 - ‘ ) _v

.

Пусть нам известно, что источник является точечным, а найти требуется зависимость мощности источника от времени, характеризуемую множителем φ(t). Подставляя (7) и (9) в (4), по- лучим интегральное уравнение Вольтерры I рода:

‘ °         1               (

[-----, exp ■

0 ² a 4ⁿ ( ‘ 0 - ‘ )     I

x 0 ²

4 a ( t ₀ - t )

^ф( ‘ ) d‘ = J ( x 0 , ‘ o ).

Заметим, что для краевой задачи теплопроводности в стержне единичной длины , рассматриваемой в работах [8, 9], функция ценности будет представляться в виде гармонического ряда с весовыми сомножителями ~ exp(– a 2 π 2 t ), что соответствует виду ядра уравнений, решаемых в цитируемых работах.

Известно, что замена интеграла в выражении (10) квадратурными формулами и сведение задачи к системе линейных уравнений часто приводит к плохо обусловленным матрицам и, как следствие, нерегулярным решениям. Тестовые расчеты для нескольких видов φ(t) подтверждают это заключение.

Регуляризация решения

Вопросы регуляризации решений интегральных уравнений I рода рассматривались во многих работах. Одним из способов получить устойчивое решение для уравнения Вольтерры I рода является сведение его к уравнению II рода путем дифференцирования. В рассматриваемом случае ядро интегрального оператора таково, что после первого дифференцирования уравнение по-прежнему будет первого рода, так как Ф ⁺ ( t 0 , t 0 ) = 0. Дальнейшее дифференцирование приводит к такому же результату.

Другим способом решения интегральных уравнений Вольтерры I рода является применение различных методов регуляризации [8, 19, 20], основная идея которых состоит в минимизации некоторого функционала от искомого решения.

Предположим, что нам известны значения функционала в разные моменты времени при фиксированном x 0 : J_k ≡ J ( x ₀, t_k ), k = 1, M.

Зададим две сетки значений моментов времени t 1 <  t 2 < … <  t N = t M , в которые необходимо определить значения искомой функции φ ( t ), входящей в выражение (10). Представим её интерполяционным полиномом Лагранжа степени n :

nn

Ф ( ‘ ) = ^ Ф ( ‘m + 1 ) П TT-j-A ■ (^H) l = 0 j = 0, j ≠ l ( t m + l ^- t m + j )

В выражении (11) значение индекса m определяет номер начального узла интерполяции и влияет на вид матрицы квадратурных коэффициентов, получающихся при подстановке выражения (11) в (10). Подставим (11) в (10) и выполним интегрирование для всех значений y_k , получим

N

Z ^Акт ^ф(t m ) = J k ,    ¹ - k - M .

m = 1

При N <  M система (12) переопределена и для её решения можно воспользоваться методом наименьших квадратов для минимизации невязки. Такой метод, в частности, реализован в пакете MATLAB для решения переопределенных систем.

В случае мгновенного протяженного источника S ( t, x ) = δ ( t ) g ( x ) подстановка данного выра-

жения и функции ценности (7) в равенство (4) приведет к уравнению:

+∞

2 a

-∞

exp f -       ■ '

V ⁴ a t 0 у

g ( x ) dx = J ( X o , t 0 ).

В данном случае момент наблюдения t 0 является параметром. Для восстановления функции g ( x ), определяющей пространственную зависимость мгновенного источника, потребуется набор значений функционала J в нескольких точках. Будем в дальнейшем для данной задачи использовать обозначение J ( y ) ≡ J ( y , t ₀).

Уравнение (13) в отличие от уравнения (10) является уравнением Фредгольма. Пробные расчеты показали, что примененный к решению уравнения (10) метод регуляризации при помощи переопределения системы линейных уравнений не дает желаемого результата. В настоящей работе для получения устойчивого решения уравнения (13) применен метод регуляризации Тихонова, заключающийся в поиске минимума функционала:

d

V = j dy

c

b                         I ²

J K ( y , x ) g ( x ) dx - J ( y )

bb

+ a J g ² ( x ) dx + a J [ g '( x )]² dx,

aa где α – малый параметр регуляризации.

При получении результатов, приведенных ниже, значение параметра α определялось простым перебором, что является приемлемым при небольшом числе расчетов и применяется рядом авторов. В общем случае пределы интегрирования в приведенном выражении должны быть бесконечными, но при построении квадратурных формул в рассматриваемом примере использовался отрезок [–7, 7], выбранный исходя из поведения функций J ( y ) и g ( x ).

Обсуждение результатов

На рис. 1 и рис. 2 приведены результаты решения уравнения (10) для различных характеров поведения искомой функции φ ( t ). На рис. 1 представлены расчеты для монотонно изменяющихся функций φ ( t ) = t 3/2 и φ ( t ) = exp( - 3 t /2). Значения второй функции на заданном интервале поиска изменяется на шесть порядков. Из рис. 1 и 2 видно, что при выбранных параметрах расчетов решения ведут себя регулярно и точность вполне достаточная. Расчеты проводились для шага по времени Δ t = 0,25 и M = 2 N .

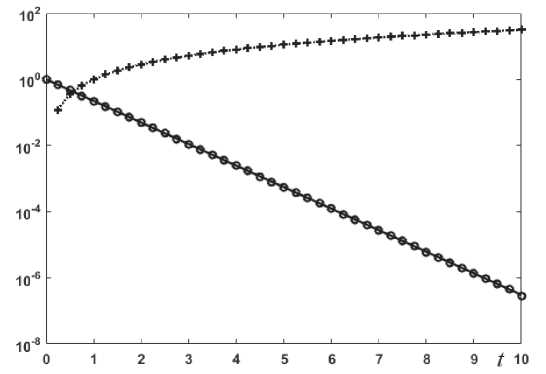
Рис. 1. Результаты решения уравнения (10) для монотонных источников.

Линии – точное исходное значение, +, о – численное решение; + – φ ( t ) = t ^3/2 , o – φ ( t ) = exp( - 3 t /2)

Математика

На рис. 2 приводятся результаты решения уравнения (10) для источников с гармонической составляющей: ф ( t ) = 1 + sin(5 t ) и ф ( t ) = 1 + sin(2 t ) /(2 t ). В обоих случаях решалась переопределенная система линейных уравнений с количеством уравнений в два раза большим числа неизвестных. И в этом случае решения ведут себя регулярно и для выбранной сетки с шагом A t = 0,2 достигается хорошая точность.

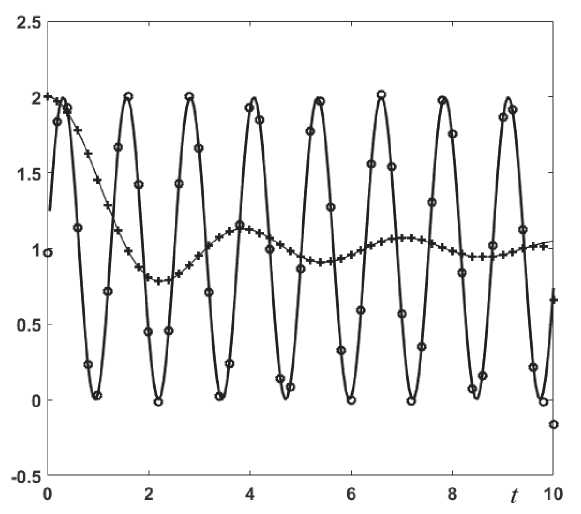
Рис. 2. Результаты решения уравнения (10) для источников с гармонической составляющей. Линии – точное исходное значение, +, о - численное решение; + - ф ( t ) = 1 + sin(2 t )/(2 t ) , o - ф(t ) = 1 + sin(5 t )

На рис. 3 представлены результаты решения уравнения (13) путем минимизации функционала Тихонова. Параметр регуляризации подбирался вручную из условия отсутствия осцилляций (разболтки) решения. Из рис. 3 видно, что рассматриваемый метод позволяет получить удовлетворительную точность для гладких функций. Несколько хуже результат получился для источника в виде прямоугольного импульса.

Заключение

Использованное в работе для определения функции источника представление функционала в форме (4) имеет общий вид для задач тепло- и массообмена, других задач переноса частиц и излучений. Нахождение ядра интегрального оператора сводится к нахождению обобщенного решения (функции Грина) уравнения переноса (в рассматриваемом случае – диффузии). Для многих задач теории переноса обобщенные решения известны, это позволяет сформулировать задачу определения источника сразу в виде интегрального уравнения первого рода с известным ядром.

Приведенные в работе результаты модельных расчетов для различных типов функций источника уравнения диффузии показывают, что использованный в работе метод решения уравнения Вольтерры I рода путем сведения задачи к переопределенной системе линейных уравнений позволяет получить устойчивые решения. Из приведённых результатов видно, что при выбранных параметрах расчетов полученные предлагаемым методом решения ведут себя регулярно и обладают вполне приемлемой точностью даже несмотря на то, что значения искомой функции на заданном интервале поиска изменяются на шесть порядков. В этом мы видим главное отличие нашего метода от других подходов к решению данной задачи.

Авторы благодарны Российскому фонду фундаментальных исследований за финансовую поддержку работы (грант 18-51-53018) .

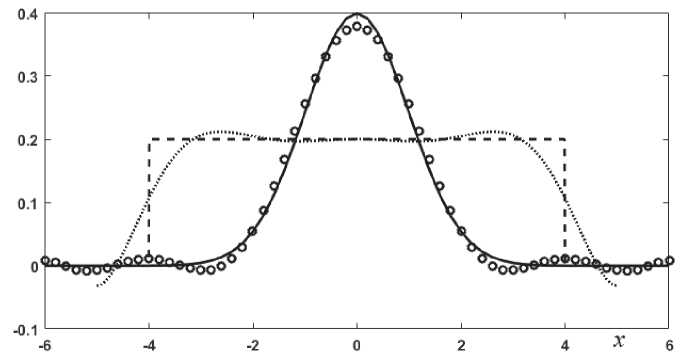
Рис. 3. Результаты восстановления пространственного мгновенного источника. Сплошная линия и пунктир – точные решения. Маленькие точки и кружки – результат решения уравнения (13). Сплошная линия и кружки – g ( x ) ~ exp(– x ²/2). Пунктирная линия – прямоугольный импульс