Метод спектрального разложения для анализа системы со сдвинутыми эрланговским и гиперэрланговским распределениями

Данная работа посвящена анализу системы массового обслуживания (СМО) E 2 /HE 2 /I со сдвинутыми эрланговским входным потоком требований и гиперэрланговским распределением 2-го порядка времени обслуживания в системе, которая обозначена E 2 /HE 2 / 1 , где знак «-» означает сдвиг закона распределения вправо от нулевой точки на величину t ₀. Как известно из теории массового обслуживания, среднее время ожидания является основной характеристикой для любых СМО. По этой характеристике оценивают задержки пакетов в сетях пакетной коммутации при моделировании телетрафика с помощью СМО. Рассматриваемая СМО E 2 /HE 2 / 1 по символике Кендалла для их классификации относится к типу G/G/1.

В теории массового обслуживания исследования систем G/G/1 актуальны в связи с тем, что они активно используются в современной теории телетрафика, хотя необходимо заметить, что при моделировании активного сетевого оборудования с ограниченным буфером системы с неограниченным временем ожидания могут быть использованы только в первом приближении [9]. В пакетах имитационного моделирования также предусмотрено использование систем G/G/1 при частных законах распределений [10].

Метод спектрального разложения решения интегрального уравнения Линдли (ИУЛ) в ис-

следовании систем G/G/1 играет важную роль, и большинство результатов в теории массового обслуживания получены именно с помощью данного метода. Одна из форм ИУЛ выглядит так [1]:

V (у ) =

<

y

I

-да

V ( у - u ) d C ( и ) ,

⁰ у <  °

у >  0;

где I V ( у ) - функция распределения вероятностей (ФРВ) времени ожидания требования в очереди; C ( и ) = P ( U <  и) - ФРВ случайной величины и = x - t , где, в свою очередь, x - случайное время обслуживания требования; t - случайная величина - интервал времени между поступлениями требований.

При кратком изложении метода решения уравнения Линдли будем придерживаться подхода и символики автора [1]. Для этого через A*(s) и В * ( s ) обозначим преобразования Лапласа функций плотности распределения интервалов между поступлениями и времени обслуживания соответственно. Суть решения интегрального уравнения Линдли методом спектрального разложения состоит в нахождении для выражения A * ( - s ) ■ В * ( s ) -1 представления в виде произведения двух множителей, которое давало бы рациональную функцию от s . Следовательно, для нахождения закона распределения времени ожидания

необходимо следующее спектральное разложение: A * ( - s ) • B * ( s ) -1 — v₊ ( s ) / V - ( s ) , где V₊ ( s ) и V - ( s ) — некоторые рациональные функции от s , которые можно разложить на множители. Функции v , ( s ) и V - ( s ) должны удовлетворять следующим условиям согласно [1]:

• 1.    Для Re ( s ) > 0 функция v₊ ( s ) является аналитической без нулей в этой полуплоскости;

• 2.    Для Re ( s ) <  D функция V - ( s ) является аналитической без нулей в этой полу-   (1)

плоскости, где D - некоторая положительная константа, определяемая из условия:

a (t)

lim      < м .

t ^ю e ^- Dt

Кроме того, функции v+ (5) и v- (s) должны обладать следующими свойствами:

lim

| s| ^® ,Re ( s ) > 0

^V +^{( s} ) = 1 ; s

^V -^{( s} ) -------— -1 .

lim

|s | ^® ,Re ( s ) < D

s

• 1.    Постановка задачи

• 2.    Решение задачи для системы E-2/HE-2/1

В работе ставится задача нахождения решения для среднего времени ожидания требований в очереди в СМО E 2 /HE 2 / 1 со сдвинутыми эрлан-говским (E ^— ) и гиперэрланговским (HE 2 ) входными распределениями с использованием классического метода спектрального разложения решения ИУЛ. Для других систем применение этого метода рассмотрено в работах [2; 6-8]. Вопросы аппроксимации законов распределений подробно освещены в [3-5], а новые исследования по системам массового обслуживания приведены в [11–14].

Рассмотрим СМО E ^— /HE ^- / 1 , для которой законы распределения входного потока и времени обслуживания задаются функциями плотности:

|4Х ² ( t - t₀)e ^{- 2 Х(} t ^- t ⁰ ) , t >  t ₀;

a ( t ) —^       ^{(      0} )              ’         ⁰                       (3)

^0 , 0 <  t <  t 0 ,

4 q ц 2 ( t - 1 ₀ ) e ^{2 Ц 1 (} t t ⁰ ) +

ь ( t ) = ^<+ 4 ( 1 - q ) ^ц 2 ( t - 1 0 ) e ^{2 ц} 2 ⁽ t t ⁰ ) , t > 1 0 ;

0 , 0 <  t <  t 0 .

Как видно из распределений (3) и (4), они при параметре сдвига t0 = 0 обращаются в обычные распределения, и в этом можно заметить преемственность обычных систем и систем с запаздыванием во времени.

Запишем преобразования Лапласа функций (3) и (4):

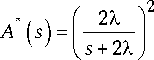
- te^s e ⁰

;

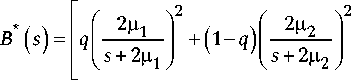
- te^s e ⁰

В этом случае выражение для спектрального разложения решения ИУЛ примет следующий вид:

V ₊ ( ^s ) Г 2X ) ² _v ----H- — I         I e ⁰ x

V - ( s ) ( 2X- s J

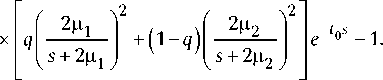
Здесь экспоненты из-за противоположных знаков обнуляются, и тем самым операция сдвига законов распределений нивелируется.

Представим выражение, стоящее в квадратных скобках, в виде

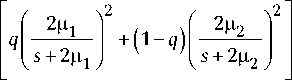
b 0 + b 1 s + b 2 s ²

=             2_X2 ^,

( s + 2ц 1 ) ( s + 2^ 2 )

где промежуточные параметры обозначены b ₀ = = 1бц 2 ц 2 , b 1 = 16Ц 1 Ц 2 [ q Ц 1 + ( 1 - q ) ^ 2 ], b 2 = 4 [ q ^ ² + + ( 1 - q ) ц 2 ]. Продолжая спектральное разложение (5), получим:

• V ₊ ( s )         4X ² ( b ₀ + b 1 s + b ₂ s ² )

• ^V -^{( s} ) ( 2X- s ) ² ( 2ц 1 + s ) ² ( 2ц 2 + s ) ²

( 2X- s ) ² ( 2ц 1 + s ) ² ( 2ц 2 + s ) ²

( 2X- s ) ² ( 2ц 1 + s ) ² ( 2ц 2 + s ) ²

• -    s ( s - d 4 s - d 3 s - d 2 s - d ^ s - d 0 )

( 2X - s )^ ( 2ц ^ + s ) ( 2^ 2 + s )

• -    s ( s + a 1 )( s + ^ 2 )( s + ^ 3 )( s + ^ 4 )( s - a₅ )

( 2X- s ) ² ( 2ц 1 + s ) ² ( 2ц 2 + s ) ²

Окончательно спектральное разложение решения ИУЛ для системы E 2 /HE 2 / 1 имеет вид

V+js) _ - S ( S + 0 1 )( S + 0 2 )( s + 0 3 )( s + 0 4 )( s -0 5 ) ^y - ( ^s )        ( 21- s ) ² ( 2ц 1 + s ) ² ( 2ц 2 + s ) ²

Пояснения к разложению (6). Многочлен пятой степени в числителе разложения в случае стабильной системы Р _ т ^ / т ^ < 1

s ⁵ - d 4 s ⁴ - d 3 s ³ - d 2 s ² - d 1 s - d 0                        (7)

с коэффициентами:

d0 _ 641^1^2 [^1^2 - 1(^1 + О) + 4b1^2 ], d1 _ 16{41^1^2 (Ц1 +^2) -

• -1 [ 2ц 1 о + ( Ц 1 + Ц 2 ) ] + 4 b 2 1 },

d 2 _ 161 [( p, 1 + О ) + 2Ц 1 Ц 2 ] -

• ^- 16⁽Ц 1 + Ц 2 ^{)( 1} 2 + Ц 1 Ц 2 ),

d3 _ -4[1 + Ц1 + Ц2 - 41(Ц1 + Ц2) + 4Ц1Ц2 ], d4 _ 4(1-Ц1 -^2), имеет четыре действительных отрицательных корня -01, -02, -03, -04 (либо два действительных отрицательных корня и два комплексно сопряженных с отрицательными действительными частями) и один положительный корень 05. Исследование знака младшего коэффициента d0 показывает, что d0 > 0 всегда в случае стабильной системы, когда 0 < р < 1. С учетом знака минус перед d0 в многочлене (7) это также подтверждает предположение о наличии таких корней многочлена.

На рисунке показана комплексная s – плоскость с нулями и полюсами функции у + ( s ) / у - ( s ) , где полюсы отмечены крестиками, а нули - кружками. Нули и полюсы нужны для построения функций у₊ ( s ) и у - ( s ) в отдельности.

Принимая во внимание условия спектрального разложения (1), (2) строим функции у + ( s ) и у - ( s ) с учетом нулей и полюсов разложения:

У +^{( s ) _}

s ( s + 0 1 ) ( s + 0 2 )( s + 0 3 )( s + 0 4 ) ( 2^ 1 + s ) ² ( 2^ 2 + s ) ²

у - ( s ) _

( 21- s ) ²

^{( s -0} 5 ) .

Константа спектрального разложения –

K _ lim *+!sl _ s ^0 s

( s + 0 1 ) ( s + 0 2 )( s + 0 3 )( s + 0 4 )

_ lim ----------------------------_ s^0     (2^1 + s)2 (2^2 + s)2

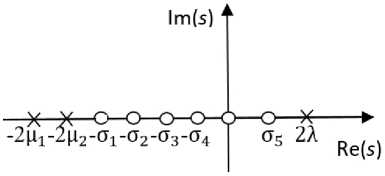
Рис. Нули и полюсы функции у₊ ( s ) / у - ( s ) для системы М/

HE2/1

Fig. Zeros and poles of the function y₊ ( s ) / у - ( s ) for the system M/HE₂/1

Эта константа определяет вероятность того, что поступающее в систему требование застает ее свободной.

Далее по методике спектрального разложения строим функцию ф+( s)_ K _ у+ (s)

0 1 0 2 0 3 0 4 ( 2Ц 1 + s ) ² ( 2^ 2 + s ) ² _--------------------------------------------------- .

16Ц 1 Ц 2 s ( s + 0 1 ) ( s + 0 2 )( s + 0 3 )( s + 0 4 )

Отсюда преобразование Лапласа функции плотности времени ожидания W ( s ) _ s -Ф₊ ( s ) будет равно

^ *( _s ) _     о,⁰ , ⁰ ; ⁰ j ( ² ^ , ^{+ s} П ²О ^{+ s} ) 2            (8)

16Ц 2 Ц 2 ( s + 0 1 ) ( s + 0 2 )( s + 0 3 )( s + 0 4 )

Для нахождения среднего времени ожидания найдем производную от функции W ( s ) со знаком минус в точке s = 0:

_ — +--+--+-----

0 1   0 2   0 3   0 4 Ц 1 О

Преобразование Лапласа (8) позволяет кроме среднего времени ожидания находить также и моменты высшего порядка времени ожидания. С учетом определения вариации задержки – джиттера в телекоммуникациях как разброс времени ожидания от его среднего значения [14], тем самым получим возможность определения джиттера через дисперсию времени ожидания.

Для того чтобы воспользоваться формулой (9) для расчетов среднего времени ожидания, необходимо задать входные параметры, в качестве которых используем значения начальных моментов первого порядка интервалов поступлений т 1 и времени обслуживания т ^ , а также их коэффициентов вариаций с 1 , c ^ . С помощью этих входных параметров необходимо определить методом моментов неизвестные параметры распределений (3) и (4) 1 , q , Ц 1 , о, а затем коэффициенты многочлена (7).

Определим числовые характеристики распределения (3) с использованием преобразования Лапласа. Средний интервал между поступлениями требований в систему E — / НЕ — / 1 равен

^Т х = ^х

^{1 +} t 0 .

и потребуем выполнения условия (14). Подставив частное решение (15) в (14), решим полученное уравнение четвертой степени q ( 1 - q )[ 8 ( 1 + c ^ ) q -- 8 ( 1 + c² ) q + 3 ] = 0 относительно параметра q с учетом условия 0 <  q < 1 и выберем нужное решение:

Второй начальный момент интервала между поступлениями равен

d ² A *( s ) ds ²

3 t _{0    2}

= F ^{+ 2}Т ⁺ t 0, s = 0  ^{2 Х} 2 ^Х

=1 ₊ 1 - ^_3(2E.z t 0J ²^_ ^{q 2} Р ^{8 [(} Тц^- t 0 ^{) 2} + c ц Т ^{2 ]} ,

откуда

2 _ ³ t 0 . 22

^Т х = —+ 2 ² - ⁺ t 0 .

2 Х ^{2    х}

Определим квадрат коэффициента вариации:

2 _г 2 _2х c х =

- ( Т х ) ²

( т_х ) ²       2 ( 1 + х t ₀ ) ²

.

Отсюда коэффициент вариации: c _х= [ 72( 1+х 1 ₀ )] ^{- 1} .

Значение первой производной функции B * ( s ) со знаком минус в точке s = 0 дает среднее значение времени обслуживания

а затем определим из (15) параметры Ц 1 и Ц 2 •

Задавая значения ту , Т ц , c х , c ц , t 0 в качестве входных параметров системы, таким образом находим известным методом моментов все неизвестные параметры распределений (3) и (4).

Теперь рассмотрим влияние параметра сдвига на коэффициенты вариаций распределений. Для эрланговского закона распределений интервалов поступлений с у = 1 / 72, и, сравнивая это с выражением (11), устанавливаем, что параметр сдвига t 0 > 0 уменьшает коэффициент вариации интервалов поступлений в 1+ Х t 0 раз. Для обычного распределения HE₂ времени обслуживания, как следует из выражений (14), получим:

^т ц = ^{q ц} 11 ^{+ ( 1 - q ) ц} 21 ⁺ t 0 ’

c

, 2 = ^{ц 2 - 2} q ^ц 2 ^{( ц} 1 ^-ц 2 ) ⁺ q ^{( 1 - 2} q ^{)( ц} 1 ^-ц 2 ^{) 2}

' ц

а значение второй производной функции B ( s ) в точке s = 0 дает второй начальный момент времени обслуживания

^{2 [ ц} 1 ^- q ^{( ц} 1 ^-ц 2 ^{)] 2}

.

^Т ц = t 0 ^{+ 2} t 0

q ₊ ^{( 1} - q )

L^

Ц 2

₊ 3 q ₊ 3 ( 1 - q )

2ц 2     2ц 2

.

Отсюда определим квадрат коэффициента вариации интервалов поступления:

c

, 2 = ^{ц 2 - 2} q ^ц 2 ^{( ц} 1 ^-ц 2 ) ⁺ q ^{( 1 - 2} q ^{)( ц} 1 ^-ц 2 ^{) 2}

■ ц

2 [ ц 1 - q ( ц 1 -ц₂ ) + t ₀ц 1 ц 2 ] ²

.

Заметим, что коэффициенты вариации < 1 / 72 и c ц > 0 при параметре сдвига t ₀

0 <  c х <

> 0 . Та-

Сравнивая последнее выражение с (14), убеждаемся, что параметр сдвига во времени t ₀ > 0 уменьшает коэффициент вариации интервалов поступлений в 1 +---^--- раз. Учитывая

[ ц 1 ( 1 - q ) + ц₂ q ]

квадратичную зависимость среднего времени ожидания от коэффициентов вариаций интервалов поступлений и времени обслуживания, убеждаемся в том, что введение параметра сдвига в законы распределения уменьшает среднее время ожидания в очереди в СМО.

ким образом, очевидно, что система Е 2 /НЕ 2 / 1 относится к типу G/G/1.

Рассматривая выражения (10)–(15) как форму записи метода моментов, найдем неизвестные параметры распределения (3) и (4). Определим параметр распределения (3) Х из (10) и получим значение Х = 1 /( Т у - 1 0 ).

Нахождение параметров распределения (4) ц , ц 2 , q будет аналогичным нахождению этих параметров для обычного распределения. Теперь, исходя из вида уравнения (12), положим:

ц1 = 2q /(тц -10), ц2 = 2(1 - q)/(тц-10),

3. Результаты вычислительных экспериментов

В таблице приведены расчетные значения среднего времени ожидания для системы с запаздыванием Е 2 /НЕ 2 / 1 для случаев малой, средней и высокой нагрузки р = 0 , 1 ; 0,5; 0,9 при значениях параметра сдвига t ₀ от 0,001 до 0,999 и коэффициенте вариации времени обслуживания с _м = 0 , 71 для обычной системы E₂/H₂/1. Значения параметров с х и с _м в системе Е₂ /НЕ₂ / 1 изменяются согласно выражениям (11) и (14). Расчеты проведены для нормированного времени обслуживания ^Т ц = 1 .

Таблица. Результаты экспериментов для СМО Е₂/Н₂ /1 при с ^ = 0,71 для системы E₂/HE₂/1 Table. Experimental results for the QS Е - /Н - /1 at, с _ц = 0,71 for the E₂/HE₂/1 system

Таким образом, данные таблицы демонстрируют качественное и количественное влияние параметра сдвига t ₀ > 0 на числовые характеристики распределений (3) и (4) и, следовательно, на основную характеристику системы - среднее время ожидания. Как и следовало ожидать, уменьшение коэффициентов вариации с _л и с _м влечет за собой многократное уменьшение времени ожидания.

Заключение

Таким образом, по результатам работы можно сделать следующие выводы.

Научная новизна результатов заключается в том, что получено спектральное разложение решения интегрального уравнения Линдли для рас-

сматриваемой системы и с его помощью выведена расчетная формула для среднего времени ожидания в очереди для этой системы в замкнутой форме. Данные численных экспериментов подтверждают полную адекватность полученных теоретических результатов.

Практическое значение работы состоит в том, что полученные результаты с успехом могут быть применены в современной теории телетрафика, где задержки пакетов входящего трафика играют первостепенную роль. Для этого необходимо знать числовые характеристики интервалов входящего трафика и времени обслуживания на уровне двух первых моментов, что не вызывает трудностей при использовании современных анализаторов трафика.

Входные параметры				Среднее время ожидания
ρ	c λ	c µ	t 0	для системы Е 2 /Н /1	для системы E 2 /HE 2 /I
0,1	0,636	0,355	0,999	0,006	0,018
	0,672	0,473	0,5	0,006
	0,700	0,645	0,1	0,013
	0,706	0,703	0,01	0,017
	0,707	0,709	0,001	0,018
0,5	0,354	0,355	0,999	0,063	0,395
	0,530	0,473	0,5	0,124
	0,672	0,645	0,1	0,321
	0,704	0,703	0,01	0,386
	0,707	0,709	0,001	0,394
0,9	0,071	0,355	0,999	0,568	4,380
	0,389	0,473	0,5	1,511
	0,643	0,645	0,1	3,578
	0,701	0,703	0,01	4,292
	0,706	0,709	0,001	4,371