Метод текстурной сегментации аэрокосмических изображений

В системах аэрокосмического мониторинга земной поверхности для решения задач анализа изображений широко применяется сегментация, которая позволяет выделить на изображениях интересующие области. Все известные методы сегментации изображений можно условно разделить на методы контурной сегментации и методы, основанные на выделении однородных (текстурных) областей. Методы на основе выделения контуров обладают высоким быстродействием, но не всегда оказываются приемлемыми при выделении на изображении областей, не имеющих четко выраженных границ и лишенных существенных деталей. В этом случае необходимо использовать идентификацию областей изображений на основе анализа их текстуры.

В [1] показано, что для описания текстуры могут быть использованы марковские случайные поля. Однако при обработке аэрокосмических изображений, представляющих собой полутоновые (или цветные) изображения с числом уровней яркости 2" , возникает проблема хранения в памяти и оперирования с матрицами вероятностей переходов размерностью 2^ х 2^. Такая обработка изображений требует больших вычислительных ресурсов. Представление g -разрядных полутоновых изображений g -разрядными двоичными изображениями (РДИ) в [2-3] позволило снизить вычислительные ресурсы за счет оперирования с матрицами вероятностей переходов размером 2×2. В статье предложен метод текстурной сегментации аэрокосмических изображений на основе марковских случайных полей, позволяющий при меньших вычислительных ресурсах эффективно выделять протяженные области с однородными статистическими характеристиками.

Метод текстурной сегментации

Пусть  g -разрядное цифровое полутоно вое изображение (ЦПИ) представлено набором g -РДИ. Учитывая характер статистической связи между элементами изображения, будем считать, что элементы ЦПИ образуют двумерную цепь Маркова с несколькими состояниями, а

РДИ – двумерную цепь Маркова с двумя равновероятными состояниями м\'\ m\ и мат- рицами вероятностей переходов по горизонтали и вертикали 2n =

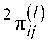
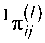
*n =

2x2

2x2

На рис. 1 представлен фрагмент двумерного / -Г0 РДИ, соответствующего марковскому слу- чайному полю. Элементами ближайшей окрес-(0

тности анализируемого элемента V 2 являются (/) (0

элементы ¥-v2 •

Так как однородная двумерная цепь Маркова полностью определяется матрицами вероятностей переходов вместе с вектором начальных вероятностей, то в качестве текстурного признака предлагается использовать оценку вероятностей перехода в двумерной цепи Маркова. Предполагается, что текстурный признак внутри одной области изменяется незначительно, а на разных областях принимает существенно различные значения. Учитывая, что основные детальные области выражены на старших разрядах ЦПИ, для их выделения необходимо обработать РДИ старших разрядов ЦПИ с наиболее выраженными текстурными признаками.

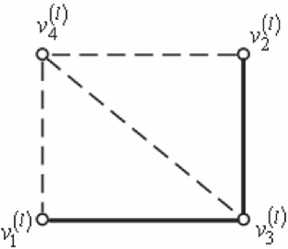
Рис. 1. Фрагмент двоичного изображения

Для определения вероятности перехода Ищ в двумерной цепи Маркова воспользуемся многомерной математической моделью изображения, синтезируемой в [2]. Вероятность состояния эле-

JO          1

мента V 2 (см. рис. 1) определится энтропией элемента относительно состояний элементов ближайшей окрестности Л,. -)vl , v2

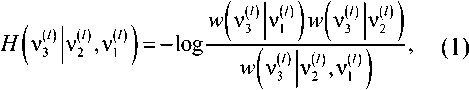
(')l (¥ (Ol (01

где ¥v3 |vi 2 wIv’- vVI – одномерные плотности вероятностей перехода между соседними

( (О I (/)\ значениями; и- vV V,',vv – плотность вероятности перехода в двумерной цепи Маркова. Плотность вероятности перехода в двумерной двоичной цепи Маркова можно выразить как

W Vj 7 v\ ,VJ 1 =

^ _n(J‘^M^\J‘^M⁽p-J‘^M^)><  (2)

i,j,4=l x8(v\l}-Mp)^Jp-Mp), где 8(") – дельта функция. На основании аргумента (1) матрица П) для сочетаний состояний элементов окрестности ^y* имеет вид:

к J 7Г J a{^ a/^ n(,)= ^ -7* = Op aP a^ a'P a;<2 up ; i*j; i = ^,g; (3) элементы которой симметричны и удовлетворяют условию нормировки aq + aq ’ = 1 "

Элементы матрицы n(,) (3) связаны с эле-

2rr(/) ментами матриц            как где 3 TtP – элемент матрицы вероятностей пере-ходов3П^ = 'п(/)х 2П(/).

Вычисление оценки 1 ™!/ вероятности перехода по горизонтали сводится к вычислению средней длины последовательности элементов одного знака [3]:

i^w =1-^212

" xu'r'

где – оценка средней длины последовательности одинаковых элементов l -го разряда на г -ом шаге уточнения оценки.

Начиная со второй строки РДИ, используя множество элементов жМ^Х’Х’Х*} и ра- нее вычисленную оценку tiV вероятности пе- реходов по горизонтали, вычисляются оценки 2 л^ И Л ^ . Учитывая локальные изменения статистических характеристик на изображении, для их вычисления используется метод «сканирующего окна» [4]. Размер окна задается исходя из заданной точности оценки и минимальных вычислительных затрат.

При обработке первых строк и столбцов изображения размер окна будет увеличиваться по мере увеличения номера обрабатываемого элемента, пока не достигнет заданных размеров. Размер окна на каждом этапе обработки определяется из пары соотношений:

w = l?(2z -l)? z = 2, ( W -1 )/2; (5) W = l,(2j-1), 7 = 2,(W-l)/2, где z, j – координаты обрабатываемого изображения, M,N – заданные ширина и высота сканирующего окна. Усредняя оценки вероятностей переходов в пределах окна, вычисляется оценка средней вероятности перехода к\'' для элемента, соответствующего центральному элементу окна:

-и-гЛ) ^iii

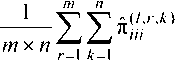
На каждом последующем шаге окно перемещается на один элемент (слева-направо, сверху-вниз) и вычисляется оценка средней вероятности перехода для каждого элемента РДИ.

Для выделения областей с разной тексту» „ „ „ рой вычисленная оценка л;7/ сравнивается с порогом. Пороговым значением h между двумя разными текстурными областями является оценка ^Ш 3 которая для текстурных областей с разными вероятностными характеристиками может быть выбрана на основе анализа гистограмм изображения. В случае когда априорно известно, что изображение содержит области двух текстур с разными статистическими характеристиками, для их выделения будет достаточно двух меток (0 и 1). Всем элементам, для которых оценка ^й превышает порог, присваивается метка 1, остальным элементам – метка 0.

В случае когда ЦПИ содержит несколько текстур, необходимо каждой из них присвоить свою метку. При этом используется несколько пороговых значений, соответствующих нескольким текстурам на изображении. Если ЦПИ содержит несколько текстур, необходимо каждой из них присвоить свою метку. При этом используется несколько пороговых значений, соответствующих нескольким текстурам на изображении.

На рис. 2 приведен пример гистограммы текстурного признака изображения, содержащего области четырех текстур с матрицами вероятно сти переходов равными:

*П = 2П =

’П = 2П =

'П = 2П =

0,75 0,25 0,5 0,5

0,25

0,75

0,5

0,5 ’

0,95

0,05

0,05

0,95

0,6 0,4

0,4 0,6

Пикселей,

0,5         0,6         0,7         0,8         0,9     ~(J)1

Рис. 2. Гистограмма текстурного признака

Число пиков на гистограмме текстурного признака изображения соответствует количеству текстур на текстурном изображении. Пороговое значение выбирается как минимальное значение между двумя соседними пиками гистограммы. Выбрав порог по тестовому набору изображений с разными статистическими характеристиками, данное пороговое значение можно использовать для сегментации других изображений, содержащих области с такими же статистическими характеристиками.

Результаты моделирования

Моделирование проводилось на реальных и искусственных изображениях, имитирующих реальные аэрокосмические изображения и содержащее естественные текстурные области в среде Matlab.

и)

б)

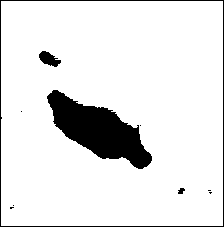
Для получения оценки качества сегментированного изображения искусственное изображение формировалось по заданной разметке. На рис.3 представлены результаты сегментации искусственного аэрокосмического изображения (размер 1024×1024 пикселей) разработанным и известными контурными методами. Сегментация разработанным и известными методами осуществлялась по 6-му РДИ. Для закрашивания контурных областей (см. рис. 3 д, ж, з), полученных известными методами, применялся построчный алгоритм заполнения с затравкой [5].

Из приведенных на рис. 3 данных следует, что разработанный метод эффективно выделяет на изображении два сегмента, один из которых относится к области леса, а другой к области озера (см. рис. 3г). Область леса однородна с точки зрения текстуры, но при этом внутри этой области присутствует большое число перепадов яркости, которые воспринимаются методами, основанными на вычислении градиента как границы областей. Известные методы выделяют значительно большее количество сегментов.

е)

Таблица 1

Тип ЦПИ	Разработанный метод	Метод Капни	Метод Собела	Метод Лапласиана гауссиана
Искусственное	0,0079	0,7665	0,4811	0,5956
Реальное	0,0388	0,7268	0,4707	0,5969

Рис. 3. Результаты сегментации искусственного изображения: а) исходное изображение; б) разметка; в) РДИ; г) результат сегментации разработанным методом; д,ж,и) контуры, выделенные методами Канни, Собела, Лапласиана гауссиана, соответственно; е, з, к) сегментированные изображения, полученные методами Канни, Собела, Лапласиана гауссиана, соответственно

Для оценки качества работы метода выделения текстурных областей и сравнения его с известными контурными методами вычислялось количество ошибочно сегментированных элементов VESEY для определения которых сегментированное изображение сравнивалось с разметкой. Результаты вычисленного критерия ESE приведены в таблице 1.

Из приведенных в таблице 1 данных следует, что ошибка сегментации разработанным методом более чем в 10 раз ниже по сравнению с известными методами, основанными на вычислении градиента. Таким образом, предложенный метод текстурной сегментации аэрокосмических изображений на основе марковских случайных полей при меньших вычислительных ресурсах эффективно выделяет протяженные области с однородными статистическими характеристиками.