Метод учета дисперсионных свойств кварцевого стекла в задачах расчета хроматической дисперсии оптических волокон

Предложен метод расчета значений показателя преломления кварцевого стекла в зависимости от концентрации легирующей присадки на заданной длине волны. Метод основан на использовании формулы Селлмейера и предназначен для применения в задачах анализа хроматической дисперсии оптических волокон (ОВ). Приведены оценки погрешностей, полученные в результате сопоставления дисперсионных характеристик ОВ, рассчитанных при использовании предложенного и известных методов учета материальной дисперсии, с экспериментальными кривыми для ОВ из кварцевого стекла, легированного германием.

Для расчета хроматической дисперсии ОВ необходимо знать спектральные характеристики распределения показателя преломления по сечению волокна. Для коаксиальных ОВ это распределение полностью описывается профилем показателя преломления – функцией, описыва- ющей изменения показателя преломления вдоль диаметра волокна. Профиль показателя преломления формируется за счет соответствующего распределения концентрации легирующих присадок. Если конструкция ОВ задается профилем показателя преломления, то для расчета хроматической дисперсии требуется решение как прямой, так и обратной задачи. А именно – расчет распределения концентрации присадки по заданному на некоторой длине волны профилю, и наоборот, расчет спектральной зависимости показателя преломления в зависимости от концентрации присадки.

Спектральные характеристики показателя преломления кварцевых стекол принято описывать дисперсионными формулами Селлмейера [1-9]:

n2

N

= i+Е

a i • Я2

i=1

λ2

^^^—

b

,

где n – показатель преломления; a i , b i – коэффициенты формулы Селлмейера; Я - длина волны.

Обычно используют формулу из трех членов ( N =3). Однако известно применение формул и более высокого порядка [10]. Основная проблема использования дисперсионных формул – ограниченный объем данных о коэффициентах a i , b i . Значения коэффициентов находят в результате обработки полученных экспериментальным путем спектральных зависимостей показателя преломления образцов стекол. Как правило, для одного типа стекла коэффициенты формулы Селлмейера известны не более чем для 4 – 5 значений концентрации легирующей добавки. При этом объединять данные, полученные для образцов разного происхождения, нельзя.

Для определения коэффициентов Селлмейе-ра и, соответственно, спектральных характеристик показателя преломления для произвольных значений концентрации легирующих добавок используют методы интерполяции. В [4-5] коэффициенты формулы находят путем интерполяции их зависимостей от концентрации присадки. Предложенный в [5] Дж. Флемингом метод 1 основан на линейной аппроксимации зависимостей коэффициентов формулы Селлмейера от концентрации присадки:

а = си + С •            ),

i        Si , i                dop , i        Si , i ,

bi = bSi,i + C " (bdop,i — bSi,i) , где C - концентрация легирующей присадки; aSi,I, bSi,i – коэффициенты чистого кварцевого

стекла; a dopi,I , b dop,i – коэффициенты чистой добавки.

В [4] описан метод 2, согласно которому коэффициенты дисперсионной формулы для произвольных значений концентрации присадки находят с помощью интерполяционных формул Лагранжа. Ограниченное число табличных значений, неравномерность шкалы аргумента при сложном характере зависимостей не позволяют говорить о возможности достижения высокой точности нахождения коэффициентов Селлмейера на основе интерполяции этих данных. Но при этом, зависимости показателя преломления от концентрации легирующей присадки, полученные при расчетах по формуле Селлмейера по этим данным для диапазона длин волн 1200 нм – 1700 нм являются достаточно гладкими (рис. 5) и, как было отмечено еще в работе Дж. Флеминга [5], их характер близок к линейному.

В [12] предложен метод 3, согласно которому коэффициенты Селлмейера определяются по результатам аппроксимации спектральной характеристики показателя преломления стекла, полученной путем интерполяции данных зависимостей показателя преломления от концентрации добавки, рассчитанных на заданной сетке длин волн. Как рекомендовано в [11], для определения коэффициентов формулы путем аппроксимации спектральной характеристики показателя преломления по формуле Селлмейера используют метод наименьших квадратов. Такой подход требует выполнения большого объема вычислений и относительно большого объема памяти, особенно в задачах синтеза ОВ.

Вместе с тем, как следует из сопоставления теоретических и экспериментальных оценок спектральных зависимостей хроматической дисперсии оптических волокон, несмотря на относительно большие погрешности определения коэффициентов Селлмейера по методу 1 и методу 2 по сравнению с методом 3, погрешности расчетов хроматической дисперсии при их использовании – величины одного порядка [12].

Следует отметить, что все рассмотренные выше традиционные методы учета материальной дисперсии в задачах прогноза хроматической дисперсии кварцевых ОВ требуют определения коэффициентов Селлмейера для заданной концентрации присадки и расчета спектральных характеристик показателя преломления и его производных на основе дисперсионной формулы Селлмейера на каждом шаге вычислений.

В данной работе предлагается метод учета дисперсионных свойств материала ОВ, основанный на линейной аппроксимации зависимости

показателя преломления кварцевого стекла от концентрации легирующей добавки:

n c = n Si ^{+ C} • (n dop - n Si )           (2)

где n C – показатель преломления кварцевого стекла с концентрацией C легирующей присадки; n dop – показатель преломления чистого материала легирующей присадки; n _Si – показатель преломления чистого кварцевого стекла; C – концентрация легирующей добавки.

Метод предусматривает предварительный расчет по формуле Селлмейера на заданной сетке длин волн спектральных характеристик показателя преломления и его первой и второй производных для чистого кварцевого стекла и чистого материала легирующей добавки (например двуокиси германия – GeO 2 ), коэффициенты Селлмейе-ра которых известны. А затем расчет по формуле (2) спектральных характеристик показателя преломления и его первой и второй производных для кварцевого стекла легированного с заданной концентрацией.

Показатель преломления в квадрате и производные этой величины определяются из (1). Значения показателя преломления и его производных связаны с этими величинами следующи- 2 ∂n     1 ∂n²

ми соотношениями: n ⁼ n ^;     =    ⋅     ^;

∂λ   2n ∂λ

∂ ² n ₌ 1

∂λ ^{2 =} 2n

∂ ² n ²      _{2 ⎜}⎛ ∂ n _⎟⎞ ²

∂λ ^{2 -   ⋅}⎝∂λ ⎠

Здесь, в отличие от традиционного подхода, формула Селлмейера используется только дважды на предварительном этапе. В процессе вычислений хроматичекой дисперсии ОВ спектральные характеристики кварцевого стекла в зависимости от профиля показателя преломления рассчитываются на основе формулы (2). Исключена необходимость определения коэффициентов дисперсионных формул. Легко решается как прямая, так и обратная задача – из (2) следует, что распределение концентрации легирующей добавки по заданному на некоторой длине волны профилю находится как:

C = n c - n Si

n dop - n Si

Все это позволяет существенно сократить объем и время вычислений, что особенно важно при решении задач синтеза ОВ. Область применения предложенного подхода можно существенно расширить, если привести формулу (2) к виду:

n Cx = n Si ^{+ C} x • ⁽ n C — n Si ) / ^C , (4)

где n _Cx , n _C – показатели преломления кварцевого стекла при концентрации легирующей присадки C _x и C, соответственно.

В этом случае достаточно знать коэффициенты Селлмейера для чистого кварца и для одного из значений концентрации легирующей добавки.

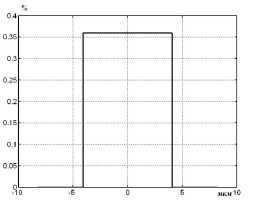
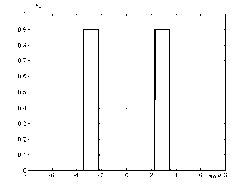
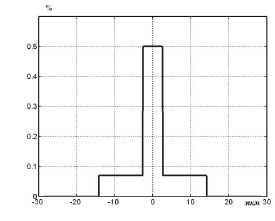
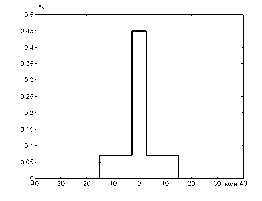
В таблице 1 представлены данные, а на рис.1 внешний вид четырех профилей показателя преломления ОВ, для которых существуют аналитические решения [1-3, 13-17] и известны экспериментальные данные спектральных характеристик хроматической дисперсии [18-20]. Для данных профилей были выполнены расчеты спектральных характеристик хроматической дисперсии при использовании предложенного метода учета материальной дисперсии и при использовании известных методов.

a)

б)

в)                                 г)

Рис. 1. Профили показателя преломления ОВ: профиль 1 ( а ), профиль 2 ( б ), профиль 3 ( в ), профиль 4 ( г )

Таблица 1. Параметры профилей показателя преломления

Тип профиля	r 1 , мкм	4 1 , %	r 2 , мкм	4 2 , %
Профиль 1	4 , 1	0 , 36	–	–
Профиль 2	2 , 85	0 , 50	14 , 23	0 , 07
Профиль 3	2 , 33	0 , 00	3 , 50	0 , 90
Профиль 4	3 , 03	0 , 45	15 , 15	0 , 07

Постоянная распространения рассчитывалась на основе известных аналитических решений [1-3,13-17]. Решение характеристических уравнений осуществлялось численными методами. Хроматическая дисперсия рассчитывалась по формуле:

D =- A.^ .106, c ⋅ λ dk 2

где D – хроматическая дисперсия в пс/(нмЧкм); в - постоянная распространения, 1/м; к = 2 -_П / Х — постоянная распространения в свободном пространстве, 1/м; X - длина волны, м; c - скорость света м/с.

Производные постоянной распространения в (5) находили численными методами. При этом использовалась аппроксимация спектральных характеристик сплайнами.

В качестве примера на рис. 2-5 приведены экспериментальные кривые и результаты вычислений дисперсионных характеристик, выполненные при использовании предложенного метода учета материальной дисперсии и при использовании известного метода 2.

Здесь 1 – экспериментальная кривая, 2 – спектральная характеристика, рассчитанная при использовании предложенного метода, 3 – спектральная характеристика, рассчитанная при использовании известного метода.

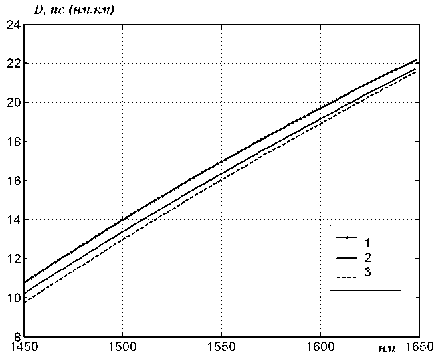
Рис. 2. Дисперсионные кривые для ОВ с профилем 1

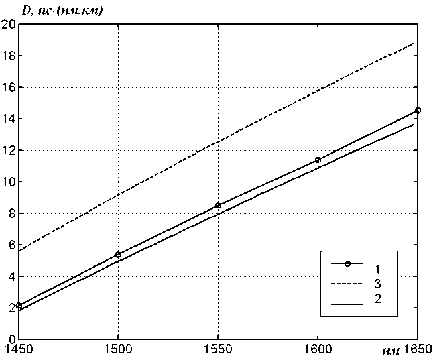
Рис. 3. Дисперсионные кривые для ОВ с профилем 2

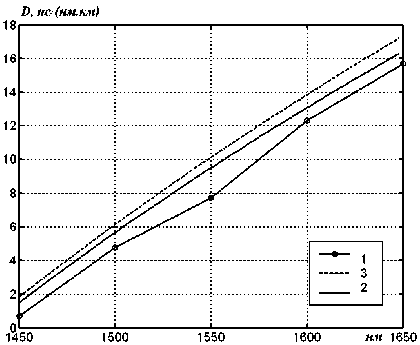
Рис. 4. Дисперсионные кривые для ОВ с профилем 3

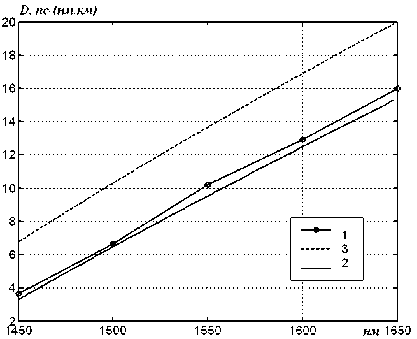
Рис. 5. Дисперсионные кривые для ОВ с профилем 4

Во всех случаях отклонение от экспериментальных оценок теоретических, полученных при использовании предложенного метода, меньше чем у полученных при использовании традиционных методов. Для профилей 1 и 3 погрешность снижается в 1,5-3,0 раза. А для профилей 2 и 4 – практически на порядок. Это позволяет рекомендовать предложенный метод для применения в задачах прогноза спектральных характеристик хроматической дисперсии кварцевых германат-ных слабонаправляющих оптических волокон, а также предположить возможность его использования при анализе характеристик ОВ другого типа.