Метод упорядочения альтернатив на основе заданных норм

На этапах проектирования и применения технических систем востребован поиск лучшего варианта. Разработке методов оценки качества и технического уровня сложных технических систем на всех этапах жизненного цикла посвящены книги С.С. Семёнова [1-3]. Оригинальный метод оценки с учётом полного жизненного цикла был опубликован в [4]. Начиная с 2010 года С.С. Семёнов проводил исследования в области создания и применения многоцелевых комплексов беспилотных летательных аппаратов (БЛА), в которых рассматривались вопросы формирования состава показателей, подлежащих оцениванию, поиска информации об их значениях для разных типов БЛА, выбора критериев, оценочных функций и весов показателей [5-14]. Эти работы позволяют принимать взвешенные решения при формировании облика проектируемых БЛА.

В качестве исходных данных для выбора варианта облика предлагалось использовать существующие образцы БЛА. При выборе наилучшего варианта образцы БЛА сопоставляются между собой по значениям характеризующих их показателей, отвечающих отношениям превосходства [15, 16]: y j <  C j , ограничение сверху (не более C j ); y j >  C j , ограничение снизу (не менее C j ), где y j - проектное, а C j - целевое значение j -го показателя БЛА, j = 1, n . Ранжирование образцов БЛА выполняется по результатам решения задачи многокритериальной оптимизации [17]. Количество критериев определяется числом n >1 оцениваемых показателей. В качестве целевого значения C j оптимизируемого j -го показателя принимается одна из границ шкалы [ y j _mm, y j max ]:

C j = y j mm — при минимизации j -го показателя,

C j = y j _max — при максимизации j -го показателя.

Облик проектируемого БЛА должен быть сбалансирован относительно граничных значений показателей, которые не всегда могут быть целевыми. Альтернативой им может быть используемое на практике понятие нормы [18, 19], которое можно распространить на перспективные значения показателей (норма меняется вместе с техническим прогрессом).

В данной работе предлагается использовать понятие нормы для выбора значений показателей перспективных вариантов БЛА. Для исследования методов упорядочения БЛА использована инструментальная системы выбора и ранжирования СВИРЬ-М [20].

1    Соотношение цели и нормы

Любая активная система чередует либо совмещает процессы сохранения и улучшения своего состояния. Для улучшения состояния она руководствуется целью , а достигнутое состояние принимается за норму , которой придерживаются в заданном промежутке времени. Таким образом, на содержательном уровне цель и норма связываются процессами сохранения и улучшения системой своего состояния. Цель - это то, что надо достигать, а норма - это то, что надо сохранять. Процессы сохранения и улучшения состояния отражают противоположные свойства стабильности и развития системы.

Формальные модели этих процессов выражаются через предикаты первого порядка на шкале оцениваемого показателя объекта x . Жёсткая цель представляется предикатом y ( x ) ^ max (min), а мягкая цель - предикатом y ( x ) >  c (y ( x ) <  c ) или словесно - значение y должно быть не менее (не более) значения C .

Норма формализуется предикатом принадлежности интервалу значений шкалы показателя: y ( x ) e [ c 1 , с ₂]. При равной важности всех значений показателя в интервале [ с 1 , с ₂] принадлежность ему выражается через совмещение двух мягких целей: C 1 <  y <  C 2 или в раздельной записи: ( y >  C 1 ) & ( y <  C 2 ).

Если в интервале выделена наиболее значимая точка, например с = ( с 1 + с ₂)/2, то норма сводится к достижению двух противоположных жёстких целей: y ( x ) ^ max, если y ( x ) <  с 1 и y ( x ) ^ min, если y ( x ) >  с ₂. Таким образом, содержательные связи между свойствами стабильности и развития системы формализуются логической связью между их моделями.

Жёсткие границы интервала [с 1, с2] следует рассматривать как частный случай отсутствия размытости границ. В общем случае границы нормы являются размытыми, что расши- ряет интервал до допустимых и предельных границ нормы. Достижение показателем предельной границы угрожает существованию объекта x.

Допустимые и предельные границы нормы выражаются соответственно через интервалы [cдом, cдоб] и [cпом, cпоб], где индексами дом (пом) и доб (поб) обозначаются допустимые (д) и предельные (п) отклонения (о) от границ нормы в сторону меньших (м) и больших (б) значений показателя. Расширению границ нормы соответствуют отношения вхождения интерва- лов: [c 1, c2] с [cДом

, c доб ] с [ c

пом

, ^c поб ^].

2    Модели нормы и решаемые задачи

Интервалы [ c _пом, c 1 ) и ( c ₂, c _поб] представляют отрезки шкалы показателя, отражающие отклонения его значения в меньшую и большую сторону от нормы. Если принять интервал [ c 1 , c ₂] за модель нормы (Н), то интервалу [ c _пом, c 1 ) ставится в соответствие класс «Меньше нормы» (МН), а интервалу ( c ₂, c _поб] - класс «Больше нормы» (БН). Этим формулируется задача классификации объекта x по оцениваемому показателю на три класса: Н, МН и БН. Границы допустимых отклонений от нормы могут быть использованы как центры области размытости между соседними классами. Примеры нелинейных функций принадлежности классам Н, МН и БН приведены в [21]. Принадлежность объекта каждому из этих классов по многим показателям вычисляется как их средневзвешенная свёртка.

Принадлежность значения показателя классам МН и БН рассматривается в задачах наблюдения состояния объекта и его управления. Моделирование развития объекта по многим показателям приводит к усложнению классификационной модели в направлении учёта показателей, требующих улучшения. В связи с этим для представления отношения нежелательности / желательности отклонения в [21] введены два дополнительных класса «Хуже нормы» (ХН) и «Лучше нормы» (ЛН). Нежелательность отклонения значения нейтрального показателя в любую сторону от границ нормы выражается через делегирование принадлежностей классам МН и БН в класс ХН. Элементы класса ЛН формируются из принадлежностей классу БН для максимизируемых показателей и из принадлежностей классу МН для минимизируемых показателей.

Результатом вычисления принадлежности объекта классам по многим показателям является вектор ц ( x ) = ( р _н( x ), Ц _хн( x ), р _лн( x )), (р_н( x ) + р_хн( x ) + р_лн( x )) = 1. Компоненты вектора отражают состояние объекта через постоянство, ухудшение и улучшение его свойств.

Качество состояния оценивается через соотношение таких свойств, как стабильность, риск и развитие. В отсутствие отклонений от нормы р_н( x ) ^ 1, что означает отсутствие как риска, так и развития. Представляет интерес соотношение р_н( x ) и р_лн( x ), как долей единицы при р_хн( x ) ^ 0. Соотношение р_н( x ) > р_лн( x ) характеризует превосходство стабильности над развитием, а р_н( x ) < р_лн( x ) отражает обратную тенденцию.

В задаче сопоставления объектов по принадлежности одному из классов выполняется их упорядочение по величине функции принадлежности этому классу. Для получения линейного порядка на множестве объектов по принадлежности всем классам требуется преобразование векторных оценок в скалярные (числовые) оценки, которые называются индикаторами состояния (ИС) объекта [21]. Они вычисляются суммированием оценочных функций, образуемых на основе критериев: р _Н( x ) ^ max, р _ЛН( x ) ^ max, р _ХН( x ) ^ min. Важность оценочных функций задаётся вектором весов: w = ( w ( р _Н( x )); w ( р _ЛН( x )); w ( р _ХН( x ))).

В отсутствие информации об их важности w ( р _Н( x )) = w ( р _ЛН( x )) = w ( р _ХН( x )) =1/3.

Если на основе статистики установлены границы уровней качества на шкале [0, 1] ИС, то существует возможность по значению ИС определить уровень качества объекта x. Для сопоставления объектов по их ИС в задаче с оптимизируемыми показателями веса всех классов должны быть ненулевыми. Для сопоставления объектов по одному из классов веса остальных классов задаются нулевыми.

Таким образом, задача упорядочения объектов по результатам классификации решается в следующей последовательности.

• 1)    задаются шкалы и нормы количественных показателей.

• 2)    задаются важности (веса) показателей.

• 3)    выполняется классификация каждого объекта относительно нормы.

• 4)    задаются важности (веса) классов.

• 5)    вычисляется ИС объекта.

• 6)    выполняется упорядочение объектов по ИС.

• 7)    по результатам упорядочения выбирается предпочтительный объект.

• 8)    для оценивания отклонений от нормы объекты упорядочиваются относительно соответствующих классов.

• 3.1    Характеристики беспилотных летательных аппаратов

3    Сопоставление методов упорядочениябеспилотных летательных аппаратов

Свойства метода упорядочения объектов по заданным нормам могут быть определены в сопоставлении с методами упорядочения с использованием многокритериальной и многомерной оптимизация объектов по ценности. Для проведения экспериментов по упорядочению БЛА разными методами принят минимальный набор наиболее значимых показателей.

В эксперименте приняты характеристики БЛА, приведённые в таблице 1 [13]:

M ВЗЛ – взлётная масса БЛА (кг);

M _БН – масса боевой нагрузки (кг);

D _П – дальность полёта (км);

T _П – продолжительность полёта (км);

H _П – высота полёта (м);

V max – максимальная скорость полёта (км/ч);

n – количество точек подвески УР, УАБ (ед.);

С БЛА – стоимость БЛА (млн. долл.).

Символом ∗ в таблице помечены экспертные оценки показателей.

Таблица 1 - Характеристики разведывательно-ударных и ударных беспилотных летательных аппаратов с взлётной массой 0,3-2,0 т. [13]

N	БЛА	Страна	M ВЗЛ	M БН	D П	T П	H П	max	n	С БЛА
1	Форпост-М	Россия	454	100	500	17,5	5000	200	2	7,5
2	Дозор-600	Россия	640	220	3700	30	7500	210	2	6
3	Байрактар ТВ2	Турция	650	150	300	24	7000	220	4	8
4	Гермес 900	Израиль	1180	350	4000	36	9145	220	2∗	12∗
5	Орион-1 (Э)	Россия	1200	200	600	24	8000	200	2	6
6	Импакт 1300	Израиль	1300	400	1500	30	9000	250	2∗	9∗
7	СН-4В	Китай	1350	345	1600	14	7000	250	4	4
8	Вин Лун-1D	Китай	1500	400	2000	35	7500	280	4	8 ∗
9	MQ-1C Грэй Игл	США	1634	478	8000	36	8840	280	4	17∗
10	Рустом-2	Индия	1800	350	900	24	10660	300	2	10

Функциональность БЛА характеризуется скоростью, высотой и продолжительностью полёта. Продолжительность полёта косвенно характеризует энергоёмкость БЛА. Она оценивается затратами электроэнергии либо топлива на дальность полёта.

Взлётная масса является классификационным показателем, который в значительной степени определяет массу полезной нагрузки БЛА. Если по значению классификационного показателя два БЛА различаются в два и более раз, они принадлежат разным категориям [14]. Согласно этому условию первые три БЛА по взлётной массе не сопоставимы с остальными БЛА, выделенными (полужирный шрифт в таблице 1) в оцениваемую группу.

• 3.2    Модель многомерного оценивания беспилотных летательных аппаратов

Показатели БЛА разделены на группы: экономические и характеристики. Для сопоставления разных методов упорядочения БЛА можно ограничиться показателями группы характеристики, которые разделены на четыре подгруппы: тактическая, техническая, боевая, выживаемость. В тактическую подгруппу включены дальность и продолжительность полёта, в техническую – взлётная масса и масса боевой нагрузки, в боевую – количество точек подвески, в подгруппу выживаемость – максимальная скорость и высота полёта.

Методы упорядочения БЛА различаются требованиями, предъявляемыми к значениям показателей.

• ■    Для метода многокритериальной оптимизации предъявляется требование максимизации значений y j → max, которое моделируется линейной оценочной функцией (ОцФ), возрастающей на шкале [ y j min , y j max ].

• ■    В качестве ОцФ для многомерной оптимизации БЛА приемлема логистическая ОцФ. Одним из её параметров является точка перегиба c j . Для сопоставимости с методом упорядочения по принадлежности классам рассматриваются два варианта задания значения c j , связанного с границами нормы:

• o    по среднему значению нормы c j 1 = ( c j н + c j в )/2;

• o    по среднему значению переднего фронта классу Н c j 2 = ( c дом, j + c j н )/2.

• ■    Для упорядочения БЛА по принадлежности классам требуется вычисление ИС БЛА [21]. Все оцениваемые показатели оптимизируемы, причём µ лн ( y j ) = µ бн ( y j ). Вычисление ИС по принадлежности одному классу осуществляется путём назначения единицы этому классу в векторе весов и нулю – остальным классам. Например, для вычисления ИС по классу Н вектор весов w = ( w ( µ Н ( x )); w ( µ ЛН ( x )); w ( µ ХН ( x ))) кодируется как w = (1, 0, 0).

Для создания модели многомерной оптимизации БЛА по отклонению от норм помимо границ шкал показателей БЛА задаются границы норм и допустимых отклонений от норм в меньшую и большую стороны от границ норм (см. таблицу 2).

В таблице 2 приняты следующие обозначения: МинГШ (МаксГШ) – минималь-	Таблица 2 - Границы шкал и норм показателей беспилотных летательных аппаратов
ная (максимальная) граница шка-		D П	M БН	ПН	n	max	H П	С БЛА
лы показателя;	МинГШ	300	14	0,16	0	200	5000	4
НГК (ВГК) Норма – нижняя	МаксГШ	8000	36	0,35	4	300	10660	17
(верхняя) граница нормы на шка-	НГК Норма	950	20	0,29	1,9	245	6900	6,8
ле показателя;	ВГК Норма	1050	22	0,31	2,1	255	7100	7,2
ДОМ (ДОБ) – допустимое отклонение в меньшую (большую) сторону от границы нормы.	ДОМ	900	18	0,28	1,5	240	6800	6,5
	ДОБ	1100	24	0,32	2,5	260	7200	7,5

Представляют интерес два варианта параметров нормы: среднее значение нормы (СН) и среднее значение расплывчатости нормы (СРН). Модель нормы содержит двусторонние требования к значению показателя.

Для оценивания степени различия / сходства рейтингов БЛА, получаемых разными методами, использованы два показателя: показатель изменения порядка мест D ( A , B ) в рейтинге

B по сравнению с A и показатель сходства рейтингов - коэффициент ранговой корреляции Кендалла r ( A , B ) [22].

Показатель изменения порядка мест D ( A , B ) измеряется в шкале [0, 1]. Значению 0 соответствует полное сходство порядков A и B , а значению 1 - их обратный порядок. Значение 0,5 означает безразличие порядков A и B . Показатель r ( A, B ) отражает сходство рейтингов A и B , представляемое коэффициентом ранговой корреляции с шкалой [-1, 1]¹. Значению 1 соответствует полное сходство рейтингов A и B , а значению -1 - их обратный порядок. Значение 0 означает отсутствие взаимосвязи между A и B .

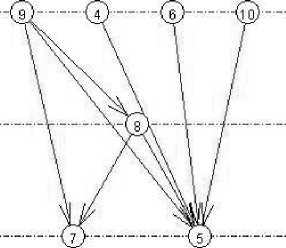
Рисунок 1 - Граф Парето-доминирования

4    Примеры упорядочения беспилотныхлетательных аппаратов

На рисунке 1 показан граф Парето-доминирования на множестве номеров2 оцениваемых БЛА {4, 5, 6, 7, 8, 9, 10}. Множество Парето-недоминируемых альтернатив представлено БЛА Гермес 900 (4), Импакт 1300 (6), MQ-1C Грэй Игл (9), Рустом-2 (10). Любой из них является кандидатом на лучший объект, для выбора которого необходимо привлечь дополнительную информацию, в качестве которой использована важность (вес) оцениваемого показателя. В отсутствие экспертных предпочтений веса показателей приняты равноценными.

В таблице 3 приведены веса составных и первичных показателей. Равноценные веса четырёх составных показателей (выделены полужирным шрифтом) рассчитываются, исходя из их числа: % = 0,25. Веса первичных показателей определяются их числом в подгруппе.

Таблица 3 - Веса составных и первичных показателей беспилотных летательных аппаратов

Показатель	Вес в подгруппе	Вес в иерархии
Характеристика БЛА	1,00	1,000
Тактический	0,25	0,250
Дальность полёта D n , км	0,50	0,125
Продолжительность полёта ТП, ч	0,50	0,125
Технический	0,25	0,250
Полезная нагрузка	1,00	0,250
Боевой	0,25	0,250
Количество точек подвески (УР и УАБ) n, ед.	1,00	0,250
Выживаемость	0,25	0,250
Макс. скорость полёта VMAKC, км/ч	0,50	0,125
Высота полёта Н П , м	0,50	0,125

Количественная оценка БЛА по всем показателям рассчитывается как средневзвешенная свёртка их значений.

В таблицах сопоставления рейтингов, полученных разными методами упорядочения (таблицы 4-8), методы именуются типом применяемой ОцФ, сокращённое имя которой приводится в тексте. Цифры в двух левых столбцах таблицы указывают на места, полученные БЛА при оценивании каждым методом, а цифры в правых столбцах таблицы - на различие рангов БЛА, полученных сопоставляемыми методами. Отрицательный знак указывает на повышение места БЛА, а положительный - на его понижение. Нули означают неизменность места БЛА при оценивании разными методами. Для сокращения в тексте, помечающем каждый эксперимент сопоставления методов упорядочения БЛА, используются имена ОцФ.

• 4.1    Линейные и логистические оценочные функции показателей

• 4.2    Логистические оценочные функции с точками перегиба

беспилотных летательных аппаратов

Таблица 4 - Сопоставление рейтингов с оценочными функциями Лин и «среднее значение нормы» показателей беспилотных летательных аппаратов

БЛА	ОцФ Лин	ОцФ СН	Изменение	Различие, %
MQ-1C Грэй Игл	1	1	0	0,00
Ван Лун-1D	2	2	0	0,00
Гермес-900	3	5	2	33,33
СН-4В	4	4	0	0,00
Импакт-1300	5	3	-2	-33,33
Рустом-2	6	6	0	0,00
Орион-1 (Э)	7	7	0	0,00

За базовую принята модель БЛА с линейными ОцФ Лин. С ней сопоставлена модель с возрастающими логистическими ОцФ показателей с точкой перегиба, равной СН. Например, согласно таблице 2 c 1 (D п ) = (950 + 1050)/2=1000. Результаты сопоставления полученных рейтингов БЛА показаны в таблице 4.

Изменение порядка мест БЛА составляет D (ОцФ Лин, ОцФ СН) 14,3%, а сходство рейтингов r (ОцФ Лин, ОцФ СН) 71,4% оценивается как высокое. БЛА Гермес-900 и Импакт-1300 обменялись местами (3-е и 5-е места). Учитывая параметрическую связь логистических ОцФ с нормой, БЛА Импакт-1300 в большей степени соответствует норме.

«среднее значение нормы» и «среднее значение расплывчатости нормы»

За базовую принята модель БЛА с логистическими ОцФ показателей с точкой перегиба, равной СН. С ней сопоставлена модель с логистическими ОцФ показателей с СРН. Результаты сопоставления полученных рейтингов БЛА показаны в таблице 5.

СН ОцФ равно c 2 (D п ) =

Таблица 5 - Сопоставление рейтингов с оценочными функциями «среднее значение нормы» и «среднее значение расплывчатости нормы» показателей беспилотных летательных аппаратов

БЛА	ОцФ СН	ОцФ СРН	Изменение	Различие, %
MQ-1C Грэй Игл	1	1	0	0,00
Ван Лун-1D	2	4	2	33,33
Импакт-1300	3	2	-1	-16,67
СН-4В	4	6	2	33,33
Гермес-900	5	3	-2	-33,33
Рустом-2	6	5	-1	-16,67
Орион-1 (Э)	7	7	0	0,00

1000, а СРН ОцФ равно c2(Dп) = (900 + 950)/2 = 925. Изменение этого параметра логистической функции повлияло на изменение порядка мест БЛА. Оно определено параметром D(ОцФ Лин, ОцФ СН) 19,3%. Сходство рейтингов r(ОцФ Лин, ОцФ СН) 61,9% оценивается как умеренное. Сдвиг точки перегиба логистических ОцФ с середины нормы на фронт моде- ли нормы оказывает существенное влияние на рейтинг БЛА с изменением их порядка на 19%.

• 4.3    Линейные оценочные функции показателей беспилотных летательных аппаратов и принадлежность классу Н

4.4 Логистические оценочные функции с точками перегиба «среднее значение нормы» и принадлежность классу Н

За базовую принята модель БЛА с ОцФ Лин. С ней сопоставлена модель с функциями принадлежности классу Н. Результаты сопоставления полученных рейтингов БЛА показаны в таблице 6.

Таблица 6 - Сопоставление рейтингов с оценочными функциями Лин и функциями принадлежности классу Н показателей беспилотных летательных аппаратов

БЛА	ОцФ Лин	Класс Н	Изменение	Различие, %
MQ-1C Грэй Игл	1	6	5	83,33
Ван Лун-1D	2	7	5	83,33
Гермес-900	3	2	-1	-16,67
СН-4В	4	4	0	0,00
Импакт-1300	5	1	-4	-66,67
Рустом-2	6	5	-1	-16,67
Орион-1 (Э)	7	3	-4	-66,67

Изменение порядка мест БЛА составляет D (ОцФ Лин, ОцФ СН) 66,67%, а сходство рейтингов r (ОцФ Лин, ОцФ СН) 33,33% оценивается как низкое. Коэффициент изменения порядка D = 66,67% отражает слабую обратную связь рейтингов.

Таблица 7 - Сопоставление рейтингов с оценочными функциями «среднее значение нормы» и функциями принадлежности классу Н показателей беспилотных летательных аппаратов

БЛА	ОцФ СН	Класс Н	Изменение	Различие, %
MQ-1C Грэй Игл	1	6	5	83,33
Ван Лун-1D	2	7	5	83,33
Импакт-1300	3	1	-2	-33,33
СН-4В	4	4	0	0,00
Гермес-900	5	2	-3	-50,00
Рустом-2	6	5	-1	-16,67
Орион-1 (Э)	7	3	-4	-66,67

За базовую принята модель БЛА с логистическими ОцФ с точками перегиба СН. С ней сопоставлена модель с функциями принадлежности классу Н. Результаты сопоставления полученных рейтингов БЛА показаны в таблице 7.

Изменение порядка мест БЛА составляет D (ОцФ Лин,

ОцФ СН) 61,9%, а сходство рейтингов r (ОцФ Лин, ОцФ СН) 21,81% оценивается как низкое. Коэффициент изменения порядка D = 61,9% отражает ещё более слабую обратную связь рейтингов в сравнении с применением ОцФ Лин.

4.5 Логистические оценочные функции с точками перегиба

«среднее значение расплывчатости нормы» и принадлежность классу Н

Таблица 8 - Сопоставление рейтингов с оценочными функциями «среднее значение расплывчатости нормы» и функциями принадлежности классу Н показателей беспилотных летательных аппаратов

БЛА	ОцФ СРН	Класс Н	Изменение	Различие, %
MQ-1C Грэй Игл	1	6	5	83,33
Импакт-1300	2	1	-1	-16,67
Гермес-900	3	2	-1	-16,67
Ван Лун-1D	4	7	3	50,00
Рустом-2	5	5	0	0,00
СН-4В	6	4	-2	-33,33
Орион-1 (Э)	7	3	-4	-66,67

За базовую принята модель БЛА с логистическими ОцФ с точками перегиба СРН. С ней сопоставлена модель с функциями принадлежности классу Н. Результаты сопоставления полученных рейтингов БЛА показаны в таблице 8.

Изменение порядка мест БЛА составляет D (ОцФ Лин, ОцФ СН)

52,38%, а сходство рейтингов r (ОцФ Лин, ОцФ СН) 4,76% оценивается как очень низкое. Коэффициент изменения порядка D = 52,38% соответствует значению 0,5 в шкале [0, 1]. Это

означает практическое отсутствие сходства между сопоставляемыми рейтингами БЛА.

Результаты упорядочения БЛА по принадлежности норме не обязательно согласуются с отношением Парето-доминирования (см. рисунок 2). Если занявший первое место БЛА Им-пакт-1300 входит во множество Парето, то входящие в него БЛА MQ-1C Грэй Игл (9) и Рустом-2 (10) получили места ниже всеми доминируемого БЛА Орион-1 (5), занявшего 3-е место. Это объясняется ужесточением требований к значениям показателей со стороны нормы.

Выполненные сопоставления рейтингов БЛА, полученных разными методами упорядочения, позволяют сделать вывод о значительном расхождении рейтингов, что объясняется различием требований к значениям показателей.

5    Оценка отклонений беспилотных летательных аппаратов от нормы

Поскольку упорядочение БЛА по принадлежности классу Н выполняется в два этапа, информация, полученная на этапе классификации, может использоваться для оценивания меры отклонений показателей от нормы. В таблице 9 приведена принадлежность БЛА классам по всем показателям. Для упорядочения БЛА по принадлежности классу Н используется класс ХН, суммирующий отклонения в обе стороны от границ нормы. Лучшим считается БЛА, имеющий наименьшее суммарное отклонение от нормы. Таковым является БЛА Им-пакт-1300 с µ ХН (Импакт-1300) 0,46. Поскольку целевым классом является Н, класс ЛН в этой задаче не учитывается.

Таблица 9 - Принадлежность беспилотных летательных аппаратов классам отклонений

БЛА	Меньше нормы	Норма	Больше нормы	Лучше нормы	Хуже нормы
Гермес-900	0,12	0,37	0,38	0,00	0,50
Орион-1 (Э)	0,42	0,29	0,19	0,00	0,60
Импакт-1300	0,00	0,39	0,46	0,00	0,46
СН-4В	0,21	0,25	0,37	0,00	0,58
Ван Лун-1D	0,08	0,00	0,92	0,00	1,00
MQ-1C Грэй Игл	0,00	0,02	0,92	0,00	0,92
Рустом-2	0,15	0,25	0,40	0,00	0,54

Оценка меры отклонений БЛА Импакт-1300 от нормы выполняется по таблице 10, в которой показатели ранжируются по кратности отклонения от ближайшей границы нормы.

Таблица 10 – Показатели беспилотного летательного аппарата Импакт-1300, имеющие отклонение от класса Н

Показатель	Значение	Норма	Отклонение
Дальность полёта D П , км	1500	[950, 1050]	1,43
Продолжительность полёта T П , час	30	[20, 22]	1,36
Высота полёта H П , м	9000	[6900, 7100]	1,27
Масса боевой нагрузки MБН, кг	400	[226, 352]	1,13

Наибольшее отклонение имеется по показателю дальности полёта в большую сторону от границы 1050 км. Полуторный запас по этому показателю отражает его избыточность по отношению к потребностям. Это касается и остальных трёх показателей с меньшей долей избыточности. Можно отметить, что в таблице 10 отсутствуют показатели с отклонением в меньшую сторону от заданных норм.

Заключение

В работе упорядочение объектов относительно выполнения односторонних требований к значениям показателей расширено на случай двусторонних требований, выраженных через понятие нормы. Определение отношения соответствия значения показателя норме относится к задачам классификации. Для учёта отклонений значений показателей от нормы в меньшую или в большую сторону требуется включение в рассмотрение двух дополнительных классов. Принадлежность объекта каждому из этих классов расширяет исходные данные для последующего упорядочения объектов в отношении превосходства. Таким образом, задача упорядочения объектов относительно нормы представляет собой двухэтапную процедуру реализации отношений соответствия и превосходства. Наряду с базовым вариантом упорядочения объектов относительно нормы имеется возможность их ранжирования относительно как каждого типа отклонения, так и в целом на основе вычисления ИС объекта.

По результатам экспериментального сопоставления известных и предложенного методов упорядочения объектов, выполненного в системе выбора и ранжирования СВИРЬ-М на примере семи БЛА, было установлено: отсутствие сходства полученных рейтингов БЛА; рассогласование рангов отдельных БЛА с отношением Парето-доминирования, построенным по односторонним требованиям к значениям показателей.