Метод усреднения в задачах о продольном ударе стержней переменного сечения

Математической моделью для многих задач динамики элементов оборудования и сооружений является стержень с переменным сечением (ударный инструмент в силовых импульсных системах, стойки и сваи различной конфигурации и пр.). Основная трудность при решении таких задач состоит в том, что собственные функции соответствующих граничных задач являются решением уравнений с переменными коэффициентами. Для некоторых частных случаев найдены аналитические решения таких уравнений, например, в работах [1, 2] рассмотрены задачи продольного удара стержней конической и гиперболической формы, в статье [3], при исследовании собственных и вынужденных продольных колебаний в конических стойках трубчатого сечения решение получено в функциях Бесселя. В работе [4] решение уравнения продольных колебаний стержня неоднородной структуры находится в виде ряда, который строится на основе рекуррентной интегральной зависимости. Тем не менее, не существует общего метода для аналитического решения таких уравнений. Поэтому для практических расчетов широкое распространение получили численные методы, в том числе и на основе аппроксимации поверхности стержней различных форм последовательно сопряженными цилиндрическими участками [5]. Однако так как численное решение можно получить исключительно для объекта с заданными параметрами, такой подход практически не применим на стадии проектных разработок. Поэтому становится актуальным вопрос об использовании методов упрощения математической модели и проведения оценок таких методов.

В работе [6] представлены различные методы приведения уравнений колебаний упругих систем к уравнениям с постоянными коэффициентами. Одним из таких методов является метод усреднения переменных коэффициентов. Такой метод был, например, использован в задаче устойчивости бурильных колон [7], а также при нахождении собственных значений для краевых спек- тральных задач четвертого порядка [8].

Рис. 1. Схема удара стержня переменного сечения о жесткий ограничитель

Поставим задачу об ударе стержня переменного сечения о жесткий ограничитель (рис. 1), принятая схема аналогична, рассмотренным в работах [1,2].

Для этого решим граничную задачу д (       дu)          д2и

I EF (x)   I = pF (x)-у , дx V       дx )д и (0, t ) = 0,(2)

и ‘(l, t ) = 0.(3)

С начальными условиями и (x,0) = 0, ut (x,0) = -vоe(x),(4)

Механика

где u (x, t) - продольное перемещение, F (x) - площадь поперечного сечения стержня, будем считать, монотонно-возрастающей на участке [0; l], E - модуль упругости, р - плотность материала, e (x) - единичная функция.

Уравнение (1) представим в виде ddUu)\d

TI F(z)т I = YF(z)^, dz V      dz)d

x

– скорость волны продольных колебаний стержня.

где z = - (0 < z < 1), у= —, c = lc

Для решения уравнения (5) применим метод Фурье. Из соотношения (5) следует уравнение для определения собственных функций Z n ( z )

Z‘ +—Z ‘+ X Zn = о, n n nn

F где An - собственные значения.

Уравнение (6) является уравнением с переменным коэффициентом. Усредним переменный коэффициент

1—(z) ,    , ,

2a = - —dz-dz = In k ,

i F(z)

где

_k = — ( 0 )

— (1)

( k <  1 ) - отношение площади поперечного сечения меньшего торца к площади

большего.

Тогда уравнение (6) представим уравнением с постоянными коэффициентами

Zn- 2aZ'n + A Zn = 0.                                (7)

Общее решение уравнения (7) имеет вид

Zn = eaz ( Qcos Pnz + C2 sin Pnz ) ,                             (8)

где P n = 7 ^x n ^{- a 2}.

Следует отметить, что при k = 1, уравнение (7) будет соответствовать уравнению для стержня постоянного сечения, а функция (8) будет его точным решением. Из граничного условия (2) находим С 1 = 0, тогда выражение для собственных функций примет вид

Zn (z) = eaz sinPnz .

Из условия (3) получим уравнение для определения собственных значений

2^ A n; - 4ln² I k ln k

в .71.7.

tan в = n, или tan. XP ln2 k = n a         n 4

Из зависимости (10) видно, что при fi n ^ 0 а ^ 1, таким образом, получаем наименьшее значение параметра k _min = 1/ e ², для которого можно определить собственные значения из уравнения (10).

На графиках рис. 2 показаны зависимости первых двух собственных значений от параметра k . Пунктирная линия отображает соответствующие зависимости, построенные на основании аналитических решений для стержней конической и гиперболической форм [1,2]. Из полученных зависимостей определяем наибольшее расхождение между значениями первого собственного числа, найденных из аналитического решения и по методу усреднения, в точке k _min составит 1,3 %, для второго, как и для всех последующих, расхождение не будет превышать 1 %. Таким образом, на основании сравнения собственных значений (собственных частот) следует вывод о том, что предложенная модель, с достаточной точностью, может использоваться для практиче-

Улитин Г.М., Царенко С.Н.

Метод усреднения в задачах о продольном ударе стержней переменного сечения ских расчетов стержней переменного сечения, у которых отношение площадей торцов не менее чем 1/e2 .

Уравнение собственных продольных колебаний с учетом первого начального условия (4) будет иметь вид:

^

u (z, t) = E AnZn (z) sin ton, n=1

где to n

A = ^C

Y 1

– частота собственных колебаний, A_n – произвольные постоянные.

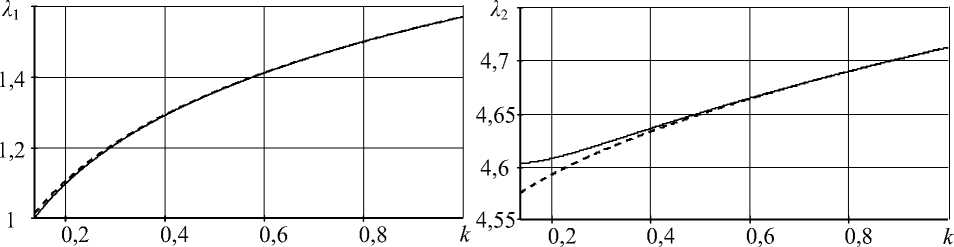
Рис. 2. Зависимость λ n от величины параметра k

Дня нахождения коэффициентов A_n , при наличии аналитического решения, используется свойство ортогональности собственных функций. В нашем случае они не будут ортогональны. Покажем, что функция Y m ( z ) = e ^{-a z} sin P m z будет ортогональна с функцией Z_n ( z ) на промежутке [0; 1] для всех m * n

J ZnYmdz = Jsin Pnz sin Pmzdz = ^2n ^2^m ( Pm tan Pn - Pn tan Pm ) , (12) 0 0 e - em так, как в * Pm, а также учитывая, что а * 0, то подставив в уравнение (12) зависимость (10)

получим f ZnYmdz = c°S ^n cos Pm (PmPn - PnPm ) = 0.

0        «(в - em)

Из второго начального условия следует уравнение

^

EAntonZn (z) = -v0e(z) .

n = 1

Умножим обе части равенства (14) на Y_m ( z ) и проинтегрируем на участке [0; 1], тогда с учетом свойства (13) получим

■ v 0 J Yndz ,

Anton JZnYndz = - откуда находим произвольные постоянные

A n

^^^^^^^в

J Y n dz v _{0 0} to ^{1 n} J Z n Y n dz 0

^^^^^^^в

c

4v0l (Л2 - а2 ) „2 - а2 - sin (2-

I2 - а2 )

.

Подставив выражение (15) в уравнение (11), получим зависимость для определения продольных перемещений сечений стержня

Механика

u ( z , t )

4 vj _a^{( 2} n   ^ ) sin(V ^{ЛЛ a} 2 z )      .

--0_e^a ^         ------- x --- sin _to n .

c     ⁿ = 1 T ? ( ² V ^Л - ^a 2 ^{- sin} (² V ^Л П ^{- a 2} ) J

Выражение для напряжений будет иметь вид:

_ ( Л - a ² ) ( a sin (V Л П - a ² z ) + V Л П - a ² cos (_x Л - a ² z ) ) ^ ( z , t ) = - E ^ v ⁰ e ^{a z} ^---------------- sin " n t .

c    n=1         431(24^-^-sin(2Vлп-a2)j

Усилие в ударном торце определяется зависимостью

4v “           I ЛЛ - a2)3

P ( t ) = - EF ₀4 v 0E                ----- ) ,_______xx sin ® n t ,

c n=1 дйТ |2VлЛ - a2 - sin (2VлЛ - a2))

где F ₀ = F ( 0 )

В работе [5] представлены результаты численных исследований на основе аппроксимации конической поверхности стержней последовательно сопряженными цилиндрическими участками. В качестве базовой модели был принят стержень постоянного сечения диаметром d0 = 0,025 м и длиной l = 1 м, конические стержни, по отношению к базовому, имели такой же диаметр ударного торца и массу, а углы уклона φ, составляли: 0,5°; 1°; 3°; 6° и 9°. Для сравнения результатов, найденных численным методом и методом усреднения, определим расчетное значение параметра k для конических стержней по формуле [2]

,

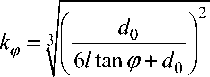
откуда находим: к ₀,₅ = 0,471; k 1 = 0,334 ; к ₃ = 0,176 ; к ₆ = 0,113 ; к 9 = 0,087. По полученным значениям видим, что для стержней с уклоном 6° и 9° рассматриваемый метод не применим, так как соответствующие значения к меньше предельного к _min = 1/ e ² = 0,135.

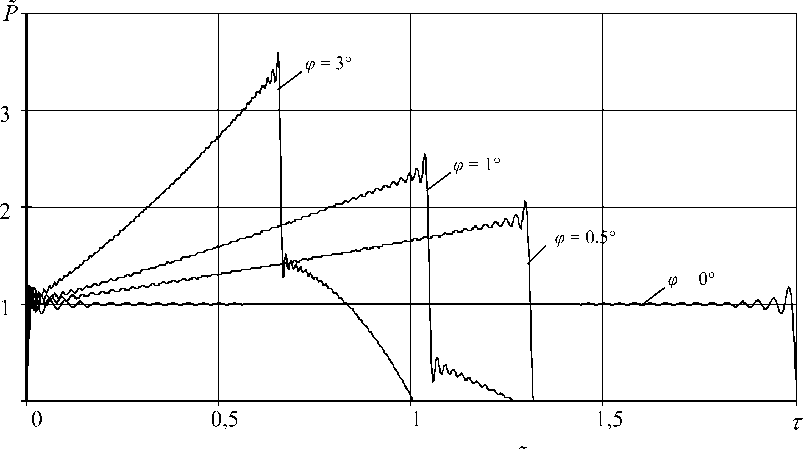
Рис. 3. Зависимость величины усилия в ударном торце P от безразмерного времени τ

Улитин Г.М.,                                Метод усреднения в задачах о продольном ударе

Царенко С.Н.                                                стержней переменного сечения

На рис. 3 представлены графики безразмерной величины усилия в ударном сечении Pc                           c

P =---в зависимости от безразмерного времени т =—t для конических стержней с раз-EF0 v0                                                  l личным углом уклона φ. Графики (рис. 3) практически полностью согласуются по характеру поведения и расчетным значениям с представленными в литературе [5], например, для стержня с φ = 3° Pmax = 3,632 [5], а максимальное значение, найденное из зависимости (16), Pmax =3,595, т.е. расхождение составляет порядка 1 %.

На основании полученных результатов, можно сделать вывод, что метод усреднения переменных коэффициентов дает достаточную точность для технических расчетов в моделях продольного удара стержней переменного сечения. При этом он ограничен предельной величиной соотношения площадей поперечных сечений, а также условием монотонности изменения площади в пределах длины стержня или участка. Учитывая, что полученные расчетные формулы не зависят от формы сечения и очертания стержня, то данный метод, с достаточной точностью для инженерных решений, дает обоснование выбора шага (участок длины стержня, в пределах которого отношение площадей сечений составляет менее чем 1/ e 2 ) для аппроксимации сложных поверхностей участками конической или другой формы, для которой известно аналитическое решение.