Метод возмущений и точные решения уравнений нелинейной динамики сред с микроструктурой

В задачах волновой динамики деформируемых сред с микроструктурой [1] часто приходится иметь дело с нелинейными уравнениями градиентного типа, содержащими слагаемые с пространственными производными высокого порядка, характеризующими нелинейность, дисперсию и диссипацию. В настоящее время существует класс эффективных методов построения точных солитоноподобных решений таких уравнений на основе их аналитической структуры [2]. При этом практически все процедуры реализуются вне методов возмущений [3]. Это понятно, так как солитоны, являясь существенно нелинейными образованиями, не могут быть получены ни в каком конечном порядке метода возмущений на основе линеаризованного решения [4, 5].

Цель данной статьи состоит в том, чтобы расширить представления о возможностях метода возмущений при решении нелинейных уравнений в частных производных и предложить эффективную методику построения их точных уединенно-волновых решений.

Рассмотрим уравнение Кортевега-де Вриза (КдВ), используемое как базовое при изложении новых методов наиболее часто:

и, + U _xxx + ии _х = 0.

Перейдя к «бегущей» переменной z = кх — ю t , после интегрирования по z получим обыкновенное дифференциальное уравнение для функции u ( z )

и "-4- и + -1г и 2 = 0,(1)

k3

решение которого построим в форме функционального ряда с формальным параметром б :

и = Ёбkuk (z).

к = 1

Подставив (2) в (1) и сгруппировав члены по степеням б , придем к системе уравнений для функций u _k :

и ,"— 4 U = 0,

1 k 3 1 ,

	1 u 1 2
и3 —uU= = 2 k 32	— к? Ч

ю„ - 1

и_л--uU= =-- uU_aU₃ ,

3 k33

„ ю        1 ( и 4 — 7W и 4 = — ТУ I и1и 3 +V I, к       к ^

Уравнение (3)1 системы является однородным и имеет частное решение и1 = exp (z) при условии ю = к3, представляющем собой дисперсионное соотношение линеаризованной задачи (1). Структура правых частей остальных уравнений позволяет отыскать их решения в форме ип = КпиП, где n — номер уравнения, Kn — постоянный множитель. Последовательно проанализировав уравнения, начиная с (3)2, определим множители Kn и придадим выражению (2) форму степенного ряда y2

и = у--? +

6 k ²

y ³ y ⁴

—

48 k ⁴ 432 k ⁶

5 y ⁵          y ⁶

+--А--- т—

20736 k ⁸ 41472 k ¹⁰

где у = б и 1 .

Заметим, что на этом этапе проделанные выше очевидные действия дублируют результаты Хироты, приведенные во введении его основной статьи [6], содержащей изложение знаменитого билинейного метода построения N -солитонных решений и преобразований Бэклунда. Хирота отмечает, что ряды вида (4) «…не сходятся быстро и даже расходятся. …Хотя мы можем построить Паде-аппроксиманту прямо из степенного ряда (4), значительно интереснее преобразовать первоначальное уравнение к специальному виду, удобному для использования Паде-аппроксиманты» [6]. Объектом дальнейшего рассмотрения будет ряд (4), непосредственно возникший при решении уравнения КдВ методом возмущений.

Как известно, диагональные аппроксиманты Паде являются наилучшими приближениями суммы степенного ряда [7]. Диагональную аппроксиманту [ N / N ] для ряда (4) представим в виде рациональной дроби, числитель и знаменатель которой есть полные многочлены порядка N с неопределенными коэффициентами:

a 0 + a 1 у + ... + a _N y ^N 1 + b у + ... + b N У ^N

Для отыскания этих коэффициентов приведем к общему знаменателю разность выражений (4) и (5) и сгруппируем слагаемые в числителе по степеням у . Приравняв нулю первые 2N +1 таких слагаемых, получим систему линейных уравнений для установления коэффициентов (5). По найденным таким образом выражениям для нескольких первых диагональных аппроксимант ряда (4)

/1] = 6^ , [2/2] = / 144 k⁴\ 2 , [3/3] = / ¹⁴⁴ k⁴\ 2 , [4/4] = / ¹⁴⁴ k⁴yV , ...

• ^{6 k} + у             ( 12 k ² + y )             ( 12 k ² + y )              ( 12 k ² + y )

видно, что начиная с порядка [2/2], они перестают изменяться. Это означает, что ряд (4) является геометрическим, и аппроксиманта [2/2] дает его точную сумму. Действительно, представив [2/2] в форме суммы бесконечно убывающей геометрической прогрессии

144k4 y    a23

[2/2] =---------- =----= a + aq + aq + aq +...,

(12 k2+y)

yy где a = y, q =------ , легко проверить, что ряды (4) и (6) совпадают.

6 k ² 144 k ⁴

После обратной замены y = &  exp ( kx -ю t ) из аппроксиманты [2/2] вытекает известное односолитонное решение уравнения КдВ:

144 k 4е exp (kx - k31)        „ f 1 (      „

.

и =-------------------------= 3k2 sech2I I kx - k31 + In I2"

(12 k2 +f exp (kx - k31))              121v

Напомним, что к ведущим членам [2] эволюционных уравнений относятся слагаемые со старшей производной и старшей нелинейностью, то есть и" и и ²/ ( 2 k ² ) в случае уравнения (1). Подставив в них вместо и степенную функцию a y ^в , найдем, что равенство ведущих членов достигается при р = - 2 , следовательно, решение уравнения (1) обладает полюсом второго порядка. Физический смысл приравнивания ведущих членов состоит в том, что для существования солитоноподобного решения необходимо, чтобы дисперсия и нелинейность, характеризуемые ими, компенсировали друг друга. Решение (7), последовавшее из аппроксиманты [2/2], также имеет полюс второго порядка. Таким образом, анализ ведущих членов уравнения позволил установить младшую аппроксиманту [ N / N ], начиная с которой следует искать последовательность совпадающих аппроксимант.

Другими словами, применение диагональных аппроксимант Паде перестраивает ряд метода возмущений для уравнения КдВ в геометрический таким образом, что сумма ряда совпадает с соответствующей аппроксимантой и дает точное решение исходного уравнения. Основной результат здесь состоит в том, что точное солитонное решение возникает не в каком-то конечном порядке, а в предельном случае — в виде суммы геометрического ряда метода возмущений. Этот результат носит принципиальный характер: он не опровергает тезис о невозможности получения солитона в конечном порядке метода возмущений, но определяет точное солитонное решение как сумму ряда при условии его геометричности.

С вычислительной точки зрения метод возмущений при отыскании точных решений уравнений нелинейной волновой динамики состоит из двух последовательных этапов: построения степенного ряда и требования его геометричности. Критерием геометричности ряда служит постоянство значений последовательных диагональных аппроксимант Паде, минимальный порядок которых обуславливается порядком полюса искомого решения, и сумма ряда представляет собой точное решение исходного уравнения. Заметим, что для эффективного использования данного критерия нужно, чтобы соответствующий степенной ряд содержал все натуральные степени переменной.

Как правило, метод возмущений для неинтегрируемых уравнений с постоянными коэффициентами приводит к слишком громоздким степенным рядам, что затрудняет вычисления с ними в ручном режиме. Зачастую выражениями для аппроксимант Паде порядков выше [3/3] непросто оперировать даже с использованием современных компьютерных систем символьной математики типа Maple или Mathematica. Кроме того, для применения метода возмущений с аппроксимантами Паде необходимо, чтобы степенной ряд соответствовал функции с полюсом целого порядка. Поэтому, если ряд характеризует функцию с полюсом нулевого, дробного или целого порядка выше второго, следует преобразовать ряд таким образом, чтобы он соответствовал функции с полюсом первого или второго порядка. Для этого ряд метода возмущений можно почленно продифференцировать, возвести в рациональную степень, обратить.

2.    Решения уравнения нелинейной волновой динамики зернистых сред

Рассмотрим уравнение с кубической нелинейностью для компоненты поперечного смещения w ( т,, ) в континуальной модели цепочки круглых частиц, выведенное в [8] при моделировании распространения волн в зернистых средах:

w _тт - Aw ,, - Bw _TT,, + Cw ,,,, ± Dw ^ w ,, = 0.

Уравнения типа (8) часто возникают при асимптотическом упрощении систем уравнений движения стержней, пластин и оболочек. Такие уравнения, иногда называемые уравнениями с «двумя дисперсиями» [9], описывают широкий спектр динамических процессов: от изгибных волн в упругих системах до продольных волн в нелинейно-упругих средах. В последнем случае степень нелинейности соответствует конкретной форме нелинейного закона Гука.

Пусть уравнение характеризуется произвольным параметром нелинейности n :

wтт - Aw,, - Bwтт,, + Cw,,,, + Dw"w,, = 0, так что (8) представляет собой его частный случай при n = 2. С использованием прямого метода возмущений, обоснованного выше, построим классы точных решений уравнения (9) при различных n и сравним их с точным решением, приведенным в [8]. Посчитав коэффициенты в (9) положительными, в результате масштабирования зависимой и независимых переменных

1 D           1 =

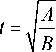
V = -/= " — w ,     x = -/=,,

BAB приведем это уравнение к виду:

v - v - v + av   + v"v = 0,

Vtt     Vxx     Vttxx        Vxxxx     Vx Vxx , где a = C/(AB).

Перейдя в (10) к бегущей переменной z = kx -tot , произведем замену зависимой переменной V ( z ) = j u ( z ) dz и проинтегрируем полученное уравнение по z . Придем к уравнению для функции u ( z ) , пропорциональной компоненте деформации среды:

u" + 5 u + X u+1 + C0 = 0,                                        (11)

где C0 — постоянная интегрирования, а коэффициенты 5 и X равны to2 - к2                         к"

к2(aк2 -to2)           (n + 1)(aк2 -to2)

Заметим, что полученное из КдВ уравнение (1) есть частный случай (11).

Рассмотрим далее уравнение (9) при разных значениях параметра n .

• 2.1.    Параметр нелинейности n = 1

В стандартном методе возмущений величина б в (2) есть малый параметр, поэтому к разложению (2) можно относиться как к решению в окрестности нуля. Отыщем более общее решение в окрестности произвольной константы E , которому соответствует выражение to

u = E + £б kuk (z).

к = 1

Подставив (13) в (11), при нулевом порядке по б получим E2X + E5 + C0 = 0, откуда C0 =-E2X- E5 , при следующих порядках, соответственно, u‘+( 2X E + 5) u1 = 0, u 2 + ( 2XE + 5) u 2 = -Xu12, u 3" + ( 2X E + 5) u 3 = -2Xu1u 2,

2        (14)

Из уравнения (14)1 найдем u1 = exp(z) при условии E = -(1 + 5)/(2X). Последовательно определив u2, u3, ... из системы (14) и обозначив у = еu1, придем к уравнению да

Ее S = у к=1

X у ² + X ² у³ X ³ у ⁴ ₊ 5 X ⁴ у⁵ 3 ⁺ 12    54 ⁺ 1296

X ⁵ у ⁶ --+... 1296

Решение уравнения (11) при n = 1 обладает полюсом второго порядка. Диагональные аппроксиманты Паде в разложении (15) равняются

[1/1] = /'7,   [2/2] = -^-2-,   [3/3] =    3^{6 у} , ...,

^X у ^{+ 3}             ( X у + 6 )             ( X у + 6 )

откуда видно, что они сохраняют постоянство, начиная с порядка [2/2]. Следовательно, ряд (15) — геометрический, его сумма совпадает с аппроксимантой [2/2]. Точное решение уравнения (11) выглядит как

1 + 5     36е ez u =---17 ,

^{2 X} ( Xe e z + 6 ) 2

является ограниченным при Xe > 0 и по форме представляет из себя солитон со сдвигом. Соответствующее решение уравнения в частных производных (10) дает компоненту смещения v v =

1 + 8,,      .36

+ C ,

-----( КХ - Ю t)--;-----;

2 X ^{v        !} X ( Xe e x ^{- -ю} t + 6 )

где 5 и X выражаются через коэффициент а и произвольные параметры к , ю посредством (12), C — постоянная интегрирования. Данное решение при 5 = - 1 имеет форму обычного кинка.

• 2.2.    Параметр нелинейности n = 2

По аналогии с предыдущим случаем при нулевом порядке по е постоянная интегрирования записывается как C0 = -E3X - E5. При следующих порядках uf+(3X E2 +5) u1 = 0, u 2 + (3X E2 +5) u 2 = -3 E X u12,                               2

u3" + (3XE2 +5)u3 = -6EXu1 u2-Xu13, ... .

Из уравнения (16) 1 найдем u 1 = exp ( z ) при

5 =-3XE2 -1.(17)

Разрешив последующие уравнения системы (16), получим

£ekuk = у-XEy2 +X(6XE2 -1)у3 -^^E(2XE2 -1)у4 + к=1                        84

+^(20X2E4 -20XE2 +1)у5 -X-E(6XE2 -1)(2XE2 -3)у6 +....(18)

При n = 2 решение уравнения (11) имеет полюс первого порядка. Проверка показывает, что начиная с [2/2], все диагональные аппроксиманты Паде для (18) остаются неизменными, равными

8 y

X ( 2 X E ² + 1 ) у ² + 8 X Ey + 8 ’

и дают точное решение уравнения (11):

,                    ⁸⁸ e ^Z

u = E +—;----;---. „ „ --------------.

X ( 2 X E ² + 1 ) 8 2 e ^{2 z} + 8 X E 8 e ^z + 8

Выразив постоянную E из (17), решение (19) можно представить в форме, содержащей только коэффициенты уравнения (11):

u = ±V-X(5 +1) +________________88 ez_________________

.

X      |(1 - 25)82 e2z ± -8= -X(5 +1)£ ez + 8

Проинтегрировав (19) по z и вернувшись к переменным x и t , получим решение уравнения (10)

v = ( kx -to t ) E + 8a arctg I       ( ( 2 X E ² + 1 ) 8 e kx ^{-m t} + 4 E )

где X определяется из (12). Решение (20) содержит четыре свободных параметра: 8 , E , k , to , и при E = 0 сводится к решению, приведенному в [8].

• 2.3.    Список точных решений при различных значениях параметра нелинейности

3.    Решения обобщенного неинтегрируемого уравнения 6-го порядка

Точные решения уравнения (11), найденные предложенным методом при различных значениях n , сведены в таблицу, где p обозначает порядок полюса решения.

Таблица. Точные решения уравнения (11)

Параметр нелинейности n	Порядок полюса p	Соотношения между постоянными	Вид точных решений
1	2	C = 0    4 X	1 + 5      62 8 e z u         +           . 2 X    ( X8 e z + 6 ) 2
2	1	( 1 25Ц ,. ( 5. 1 , C 0 = ±     зЛх	u = ± V-X ( 5 + 1 ) +________________ 8 8 e z ________________ 3 х X      X ( 1 - 2 5 ) 8 2 e2 z ±-8= y-X ( 5 + 1 ) 8 e z + 8
3	2 3	C 0 = 0, 5 = - 1	10 2/3 8 e z u =--------------- 273 ( X 8 3 e 3 z + 10 )
4	1 2	C 0 = 0, 5 = - 1	712 8 e z u = 7 X8 4e4 z + 12
1 2	4	C 0 = 0 , 5 = - 4	204 82 e2 z u =---------- 4 ( X8 e z + 20 )
3 2	4 3	C 0 = 0 , 5 = - 4	28 4/3 8 2 e 2 z u =-----------------473" ( X8 3 e 3 z + 28 )

Заметим, что в случаях дробного порядка полюса p = a/b перед вычислением аппроксимант Паде ряд метода возмущений следует возвести в степень b ; при n = 1/ 2 и n = 3/2 для избавления от радикалов в уравнении (11) необходимо перейти к новой зависимой переменной U ( z ) = ^ u ( z ) . Таким образом, в отличие от большинства методов нелинейной математической физики [2], предложенный метод в случае дробного порядка полюса решения не требует предварительного преобразования исходного уравнения для получения полюса целого порядка — вместо этого достаточно возвести ряд метода возмущений в соответствующую степень.

Рассмотрим обобщение уравнения (8), содержащее дополнительный член с шестой производной, характеризующий высокочастотную дисперсию u„ — au  — bu,, — cu ± f uu — u — 0.

tt xx ttxx xxxx          x xx xxxxxx .

Подобные уравнения возникают в задачах для сплошных сред с микроструктурой и деформируемых систем с конструктивной неоднородностью. Например, в [10] уравнение типа (21) выведено при исследовании продольных волн для компоненты продольного перемещения нелинейно-упругой ребристой цилиндрической оболочки.

Сначала исследуем (21) со знаком «—» перед нелинейным слагаемым. В соответствии с [8], такой выбор соответствует случаю «жесткой» нелинейности среды. Применим метод возмущений непосредственно к уравнению (21) и будем строить его решение в форме со u — ^еkuk (х, t).

к — 1

Подставив (22) в (21) и сгруппировав по степеням е , получим систему для функций u _k ( х , t ) :

u1 tt — au1 хх — bu1 ttxx — cu1 хххх — u1 хххххх — 0, u 2 tt — au 2 хх — bu 2 ttxx — cu 2 хххх — u 2 хххххх — 0

u3tt — au3хх — bu3«хх — cu3хххх — u3хххххх — У 2utu хх ,                              3

u4tt — au4хх — bu4«хх — cu4хххх — u4хххххх — У 2 (uLu2хх + 2u1 xU2xU1 хх ) , u5 tt — au5хх — bu5ttxx — cu5хххх — u5хххххх — У 2 (uUu3хх + 2u1 xU2xU2хх +( 2u1 xU3х + u22х ) u1 хх ) ,- из уравнения (23)1 которой найдем u1 — exp (кх — юt), при условии, что связь между ю и k задается дисперсионным соотношением ю — ± к

к ⁴ + ck ² + a

1 — bk ²

Для того, чтобы установить решения оставшихся уравнений системы (23) с номерами n — 2, 3,... в форме u n — K n u n , необходимо положить равными нулю коэффициенты K n с четными индексами n . Разрешив уравнения с нечетными номерами, для ряда (22), с учетом у — е u 1 , придем к выражению:

—      У2 (1 — bk2) у3       +____________________У4 (1 — bk2 )2 у5____________________ y 72 (—9 bk4 + ab +10 k2 + с) 2880 (—9bk4 + ab +10 k2 + c)(—25 bk4 + ab + 26 k2 + c)

У ⁶ ( 1 — bk ² ) 3 ( — 17 bk ⁴ + ab + 18 k ² + с ) у ⁷

96768 ( — 9 bk ⁴ + ab + 10 k ² + c ) 2 ( — 25 bk ⁴ + ab + 26 k ² + c )( — 49 bk ⁴ + ab + 50 k ² + c )

Преобразуем ряд (25) таким образом, чтобы он стал содержать все натуральные степени переменной y .

Для этого умножим его почленно на у и введем обозначение у — у ² . Аппроксиманта [1/1] полученного ряда запишется как

[V1] —

Y

1 +        У² ( 1 — bk ² ) Y

72 ( — 9 bk ⁴ + ab + 10 k ² + c )

Выражения для следующих аппроксимант [2/2], [3/3], … не приводим ввиду их громоздкости.

Анализ ведущих членов уравнения (21) позволяет заключить, что его решение имеет полюс 1-го порядка. Требование равенства последовательных диагональных аппроксимант, начиная с [1/1], приводит к условию с = -11 bk4 - ab +10к2.

При выполнении (26) все аппроксиманты равны 1440 к ²уД f ² у + 1440 к ² ) и предоставляют выражение для точного решения уравнения (21):

1440 s к ² e - ^to t

f 2 s 2 e ^{2 kx} 2 ■ t + 1440 к ²

6 к Vw                 s f

------sech I kx -tot + In -----;= f (        112 к VW

где to определяется равенством (24).

Заметим, что решение (28), имеющее форму классического солитона (бегущего импульса), не может быть получено с использованием методов укороченных разложений, гиперболического тангенса, простейших уравнений [2], логистической функции [11]. Аналогичная ситуация наблюдается для модифицированного уравнения Кортевега-де Вриза (мКдВ), при поиске уединенно-волновых решений которого перечисленные методы выявляют одну из двух ветвей, соответствующую гиперболическому тангенсу. Решение в виде гиперболического секанса определяется методами Хироты [6], методом проективных уравнений Риккати [12], sech-методом [13], однако анализ эффективности их применения для неинтегрируемых уравнений типа (21) является проблемой, исследование которой выходит за рамки настоящей статьи. В предлагаемом методе возмущений с аппроксимантами Паде решение (27) возникает естественно в результате его поиска в окрестности нуля.

Теперь рассмотрим случай «мягкой» нелинейности, когда в (21) перед соответствующим слагаемым стоит знак « + ». Отыскание решения по методу возмущений в окрестности линейной функции Ex , тождественно удовлетворяющей уравнению (21), в форме

№ u = Ex + ^ sкик (х, t), к=1

для функций и _к ( х , t ) дает систему уравнений

^U 1 tt ⁺ ( ^{f 2 E 2} - ^a ) ^U 1 xx - bu 1 ttxx - ^cu 1 xxxx - u 1 xxxxxx = 0, u 2 tt ⁺ ( ^{f 2 E 2} - ^a ) u 2 xx - bu 2 ttxx - ^cu 2 xxxx - u 2 xxxxxx = - ^{2 f} 2 ^EU1 x^U1 xx , u 3 tt ⁺ ( ^{f 2 E 2} - a ) u 3 xx - ^b u 3 ttxx - ^CU 3 xxxx - u 3 xxxxxx = - ^f 2 ( ^{2 EU}1 x u 2 xx ⁺ ( ^UL ^{+ 2 Eu} 2 x ) ^U 1 xx ) , u 4 tt ⁺( ^{f 2 E 2} - ^a ) u 4 xx - bu 4 ttxx - ^cu 4 xxxx - u 4 xxxxxx = - ^f 2 ( ^{2 EU}1 x u 3 xx ^{+ 2} ( ^U 1 x u 2 x ^{+ 2 Eu} 3 x ) ^U 1 xx ⁺ ( ^UL ^{+ 2 Eu} 2 x ) u 2 xx ) ,-

Уравнение (29) 1 системы имеет решение u 1 = exp ( kx -to t ) при условии

I E ² f ² - к ⁴ - ск ² - a

\       Ьк ² - 1

Решив оставшиеся уравнения системы (29) относительно функций u_k ( x , t ) , для ряда из (28) получим

/ A                 f ² E ( Ьк ² - 1 ) у ²

> sKuk ( x, t) = у + —       -------------г + к=1   "V 7      6 к (E2 bf2 + 4 Ьк4 - ab - 5 к2 - с)

f ² ( bk ² - 1 )( 3 E ² bf ² к ² + 4 bk ⁶ - 2 E ² f ² - abk ² - 5 к ⁴ - ск ² ) у ³

72 к ² ( E ² bf ² + 4 bk ⁴ - ab - 5 к ² - с )( E ² bf ² + 9 bk ⁴ - ab - 10 к ² - с ) ...

Вычислив диагональные аппроксиманты Паде для ряда (31)

[1/1] =

y

1 _          f 2 E ( bk 2 - 1 ) У

6 k ( E ² bf ² + 4 bk ⁴ - ab - 5 k ² - c )

потребуем их равенства, начиная с [1/1], как и в предыдущем случае. При выполнении условия c = VicEf (bk2 -1) + E2bf2 + 4bk4 - ab - 5k2, все аппроксиманты равны 6/10ky, (fy + 6V10"k) и дают точное решение уравнения (21):

u = Ex +

6/10 k e e kx ^{-m 1}

6/10 k + f e e kx ^{-m 1}

где го определяется из (30). При E = 0 решение (32) имеет форму бегущего фронта (кинка).

Данные результаты установлены при верхних знаках для го в формулах (24) и (30).

4.    Заключение

В статье предложен вычислительный метод получения точных решений эволюционных уравнений нелинейной волновой динамики сплошных сред, состоящий в построении степенного ряда метода возмущений и удовлетворении требования его геометричности. Показано, что солитоноподобные решения интегрируемых и неинтегрируемых уравнений представляют собой суммы геометрических рядов метода возмущений. Для уравнения, описывающего распространение нелинейных волн в зернистых средах, найдены точные солитоноподобные решения при различных значениях параметра нелинейности. При суммировании рядов метода возмущений используются их диагональные аппроксиманты Паде, порядки которых обуславливаются порядками полюсов решений уравнения. Для обобщенного неинтегрируемого уравнения 6-го порядка определены точные решения в виде бегущего фронта и бегущего импульса.

Работа выполнена при финансовой поддержке РФФИ (проект № 16-01-00176-a).