Методические аспекты применения численного прочностного анализа силового каркаса квадроцикла

Материалы и методы

Силовой каркас является одним из важнейших элементов транспортного средства (ТС), отвечающих за его заявленные эксплуатационные характеристики. Большинство рам для квадроциклов, трициклов, мотоциклов, багги и прочих подобных ТС представляют собой набор соединенных различным способом труб. Такая особенность обусловлена конструктивно-технологическими и экономическими причинами. Каркас из трубного проката является достаточно дешевым и доступным и при этом удовлетворяет таким критериям, как легкость, прочность, технологичность изготовления. Заготовки труб режут, придают определенную форму на гибочных станках, соединяя их впоследствии при помощи сварки, а также другими способами. При всей кажущейся лаконичности конструкции большинство рам квадроциклов имеют сложную пространственную геометрию, что предполагает наличие значительных трудностей в оценке локальных напряжений и деформаций в отдельных узлах и местах соединений, которые возникают под воздействием заданных эксплуатационных нагрузок.

Пространственная геометрия трубчатых рам трицикла, квадроцикла и баги в общем случае, как правило, являются расширенной функциональной вариацией «мотоциклетной» рамы. Такой конструкторский подход важен с экономической и потребительской (сервисной) точек зрения: детали и технические узлы различных ТС должны иметь определенную степень унификации деталей и узлов, что удешевляет процесс производства всей номенклатуры ТС. При этом расширение конструктивного функционала силового каркаса от мотоцикла до уровня трицикла, или квадроцикла, или баги достигается за счет присоединения к модифицированной базовой раме дополнительных силовых элементов, соответствующих типу ТС. Такая объемная модификация силового каркаса преследует две главные цели: создать условия для компоновки узлов и механизмов в зависимости от типа ТС, а также обеспечить необходимые прочностные характеристики при действии рабочих нагрузок.

Общая конструкция деталей и узлов мотоциклов и квадроциклов в достаточной мере типична для многих моделей, так же, как и типичны принципы проектирования силовых рам ТС, включая инженерный анализ [1–6]. На современном этапе развития вычислительной техники и специализированного программного обеспечения проведение большого количества натурных экспериментов при каждой модификации силового каркаса является нецелесообразным. Компьютерная трехмерная виртуальная модель трубчатого каркаса в комбинации с численным прочностным анализом состояния конструкции под действием рабочих нагрузок позволяют проводить практически безграничное количество виртуальных модификаций силового каркаса до получения желаемых прочностных характеристик. На рис. 1 представлена схема использования численного анализа для принятия оптимальных решений в отношении конструкции каркаса квадроцикла.

II

I

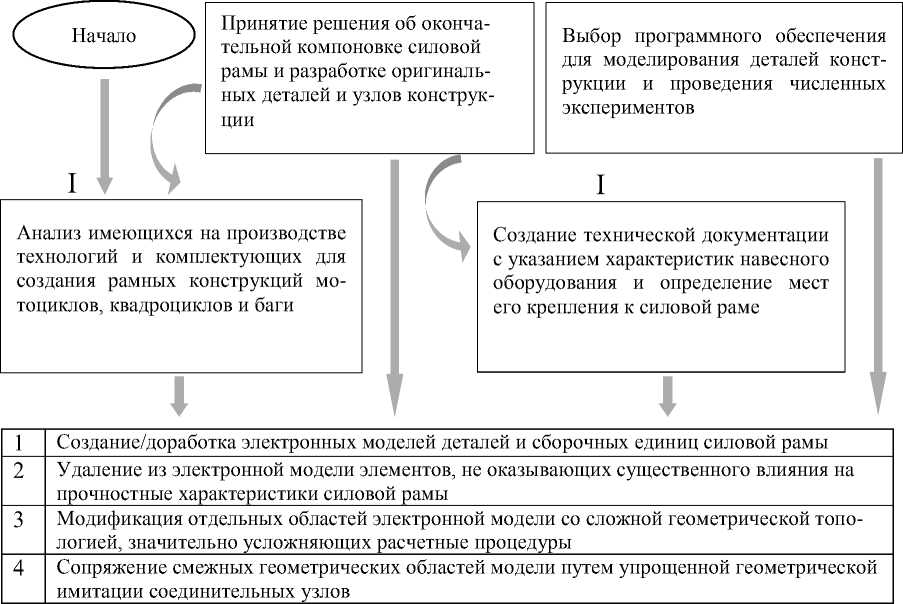
Рис. 1. Схема использования численного анализа для определения прочностных характеристик рамной конструкции силовой рамы

Численные методы моделирования

Исходя из приведенной схемы, можно видеть, что данные работы начинаются одновременно по двум направлениям (I–II). Во-первых, необходимо проанализировать имеющиеся технологические возможности предприятия и конструкторско-технологический задел, который сформировался при проектировании и производстве аналогичной продукции в прошлом. Во-вторых, необходимо принять окончательное компоновочное решение о силовой раме в соответствии с выставляемыми требованиями по размещению узлов и механизмов, а также в соответствии с эргономическими характеристиками, поскольку с некоторыми элементами рамной конструкции человек-пользователь будет взаимодействовать непосредственно. В-третьих, необходимо определиться с составом узлов и оборудования, которое крепится к силовой раме, а также с типами и формами креплений. В-четвертых, поскольку на рынке программных систем электронного геометрического моделирования и численного инженерного анализа имеется достаточно широкий выбор продуктов, необходимо определиться, какой из них является оптимальным для решения задач численного прочного анализа силовой рамы. Обобщающий блок задач (1–4), указанный на схеме, выполняется уже в виртуальной компьютерной среде одной либо нескольких выбранных программных систем.

Один из наиболее простых и понятных подходов для выполнения численного эксперимента – это выбор в пользу компьютерных систем полного жизненного цикла (PLМ-системы), что позволяет проводить работы по электронному моделированию и численному анализу в рамках одной виртуальной среды, исключая вероятность возникновения проблем трансфера численных данных между программными продуктами различных производителей.

На настоящий момент существует множество публикаций по использованию современных методов численного прочного анализа как в отношении достаточно абстрактных стержневых трубчатых конструкций [1–15], к каковым можно отнести и силовую раму квадроцикла, так и к рамам и кузовным деталям конкретных транспортных средств [16–22]. В этих источниках рассматриваются численные эксперименты, отражающие отклик конструкции на нагрузку при варьировании различных характеристик: материала изготовления, пространственной конфигурации конструкций и прочее. Во многих работах в качестве средства вычислений используются расчетные модули специализированных инженерных программных PLM-систем.

В PLM-системах для проведения численного инженерного анализа используется в основном метод конечных элементов, когда электронная геометрическая модель исследуемой конструкции преобразуется в связанную сетку прямоугольных и треугольных элементов, обладающих определенными математическими и физическими характеристиками. Однажды созданная подобная конечно-элементная модель конструкции может использоваться для бесконечного числа численных экспериментов с различными нагрузками, условиями закрепления и методами расчетов, где, если рассматривать с общих позиций, используется известный математический инструментарий.

Общее уравнение движения механической системы в матричной форме имеет вид

Mu + Cu + Ku = F ( t ) , (1) где М – матрица масс; С – матрица коэффициентов демпфирования (сопротивлений); К – матрица коэффициентов жесткостей звеньев; u^.. – вектор узловых ускорений; u^. – вектор узловых скоростей; u - вектор узловых перемещений; F ( t ) - вектор нагрузок; t - время.

В динамическом прочностном анализе происходит определение частотных характеристик исследуемой модели, что позволяет произвести качественную оценку прочностных свойств, определить вибрационную стойкость и наиболее слабые элементы конструкции.

Для определения собственных частот принимается допущение, что конструкция, подвергающаяся анализу, совершает незатухающие колебания без воздействия внешних сил. Следовательно, C = 0 и F(t) = 0 . В этом случае уравнение (1) имеет следующий вид:

• MU + Ku = 0. (2)

Поскольку уравнение линейное, а колебания для линейных систем носят гармонический характер, вектор перемещений можно записать в виде

• ^ui = ^uo^{cos (}® i^t ) , (3)

где to, - собственная частота колебаний, u_; - перемещение i -го элемента, u₀ - начальное перемещение.

После подстановки выражения (3) в уравнение (2) получаем:

• - Mu_i to. 2 cos to_t t + Ku cos to_t t = 0.

Тогда при t = 0

• ( K -to ²M ) u = 0.

Из теории линейных алгебраических уравнений подобного вида известно, что нетривиальное решение существует тогда и только тогда, когда определитель, составленный из коэффициентов перед элементами вектора u i (при u i ^ 0), имеет нулевое значение, т. е.

det ( K - Мю_}² ) = 0.

Это уравнение является исходным для поиска собственных частот колебаний исследуемой конечно-элементной модели. Решение этого уравнения является чисто математической задачей определения собственных значений, и алгоритм этого решения входит в стандартные процедуры PLM-систем.

Анализ напряжённо-деформируемой силовой рамы квадроцикла, находящегося в состоянии покоя, под воздействием массовых нагрузок со стороны навесных элементов и под воздействием силы тяжести является статической задачей. В статическом анализе вектора узловых скоростей it и ускорений U являются нулевыми, поэтому инерционные и демпфирующие компоненты выпадают из рассмотрения и уравнение равновесия (1) приобретает вид

Ku = F ( t ) .

Алгоритм решения этой задачи даже входит в стандартный расчетный модуль PLM-систем.

Результаты

В рамках работы над конструкцией квадроцикла было разработано следующее компоновочное решение (рис. 2).

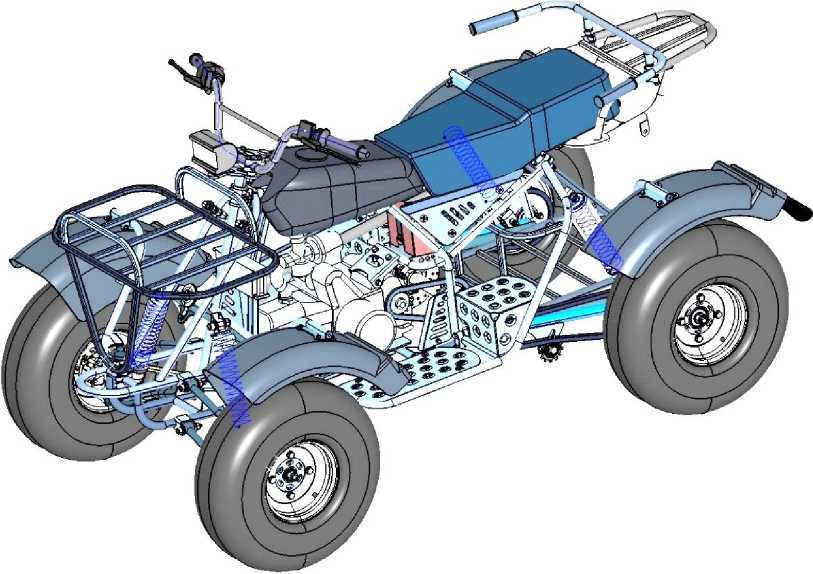
Рис. 2. Общий вид квадроцикла

Численные методы моделирования

Численный прочностной анализ силовых элементов конструкции является на сегодняшний день наиболее распространённой практикой при разработке различных типов ТС [1, 2] как в полном, так и упрощенном виде. Задачей виртуального прочностного анализа конструкции являлось выявление локализаций с пониженной прочностной устойчивостью, что должно было позволить определиться с дополнительными усиливающими элементами либо в форме отдельных деталей, либо в форме локального изменения геометрии трубчатой конструкции. Для проведения численного эксперимента полная электронная геометрия конструкции была существенно сокращена и модифицирована.

Двигатель, механизмы управления и передачи крутящего момента на колеса ТС, вес полезной нагрузки (водитель, пассажир, багаж) являются факторами, определяющими статическую рабочую нагрузку на силовой каркас. Поэтому для проведения расчетов при разработке электронной геометрической модели эти компоненты были исключены из расчетной схемы с последующим замещением на соответствующие точечные (по местам крепления узлов и механизмов) и распределенные нагрузки. На рис. 3 представлена силовая несущая рама квадроцикла.

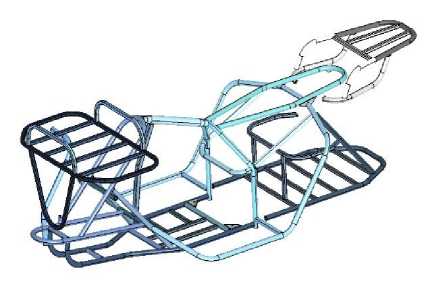
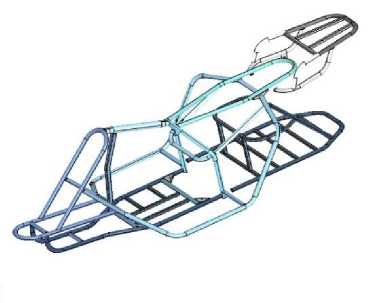
а)                                                                   б)

Рис. 3. Силовая несущая рама квадроцикла: а – с багажным сегментом, б – без багажного сегмента

В дополнение к этому виртуальная модель силовой рамы была подвергнута модификации с целью замены узлов соединения деталей упрощенными соединительными геометрическими формами. Также с учетом симметричности конструкции в расчетную схему была включена только половина геометрии: вторая половина условно моделировалась соответствующими ограничениями симметричности перемещений (рис. 4). Результирующая конечно-элементная сетка в итоге составила 647648 узлов и 2500947 элементов.

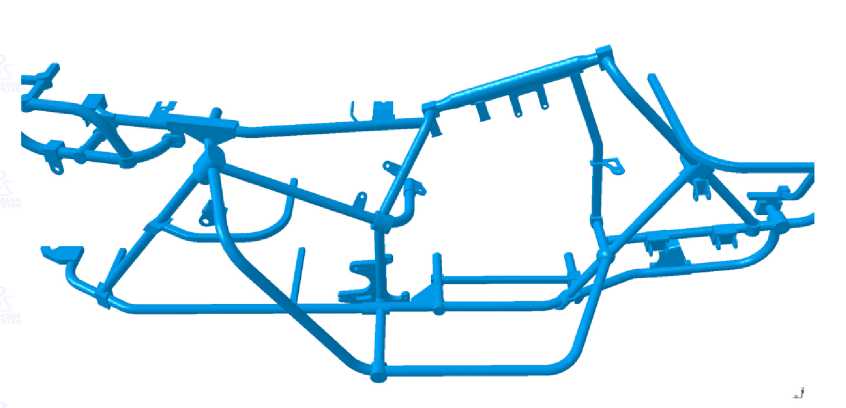
Рис. 4. Электронная модель силовой рамы для прочностного анализа

Для проведения расчетных процедур использовался материал (сталь) с характеристиками, представленными в табл. 1.

Таблица 1

Характеристика материала расчетной модели

Параметр	Значение
Материал	сталь
Модуль Юнг	2e11N/м2
Коэффициент Пуассона	0,266
Плотность	7860 кг/м3
Предел прочности	4,6 е8 N/м2

Таким образом, с учетом характеристик материала структурная масса модели (половина модели силовой рамы с учетом упрощения ее симметричности по осевой плоскости) составила 22,8 кг. Схема граничных условий и определения нагрузки конструкции силовой рамы представлена на рис. 5, где большими желтыми кругами отмечены массовые нагрузки на раму. Характеристики конечно-элементного разбиения расчетной модели представлены в табл. 2.

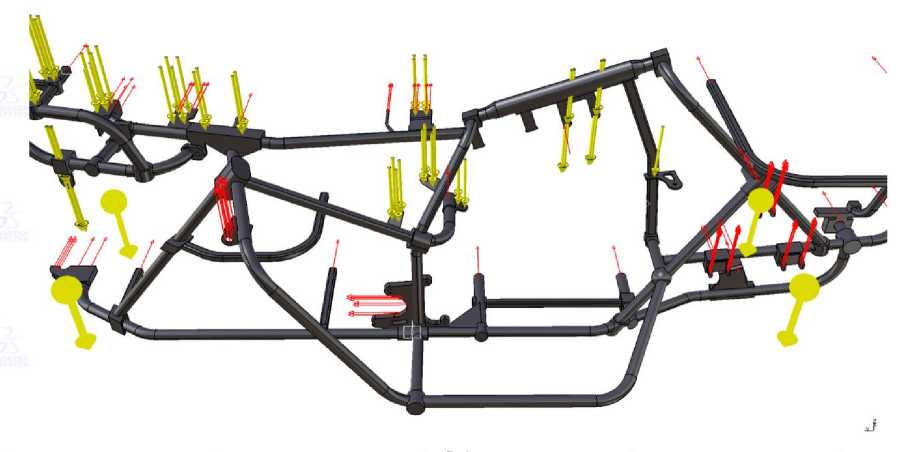
Рис. 5. Схема начальных и граничных условий при проведении статического прочного анализа

Таблица 2

Характеристики конечно-элементной модели

Параметр	Значение
Количество линий	1942944
Количество коэффициентов	36277671
Количество блоков	73
Максимальное количество коэффициентов на блок	500000
Общий размер матрицы	422,58 Mb

По результатам проведения численного прочностного анализа при статических нагрузках были получены следующие результаты по тензору полного напряжения (рис. 6).

Численные методы моделирования

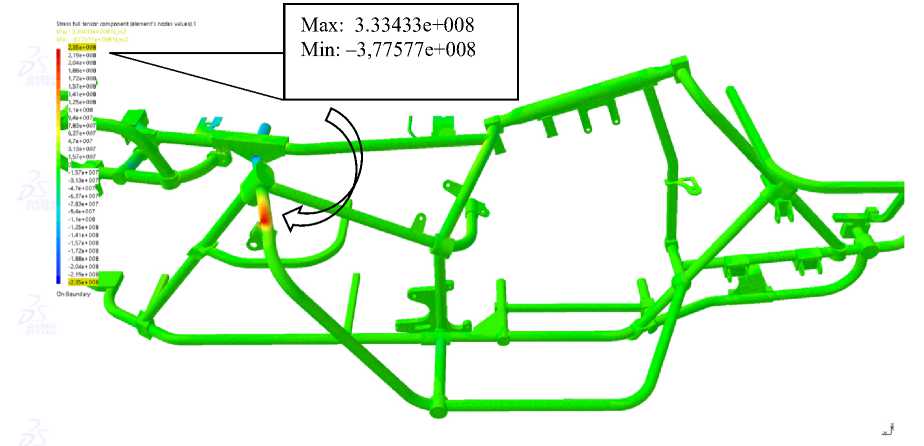
Max: 3.33433e+008

Min: –3,77577e+008

Рис. 6. Картина напряженно-деформируемого состояния трубчатого каркаса силовой рамы квадроцикла

Обсуждение

Как можно видеть из цветовой эпюры напряжений, в конструкции имеется область с пониженными прочностными характеристиками. Ее локализация в данном месте не является случайной. Рама квадроцикла конструкционно представляет собой обширный центральный осевой блок (как у рамы мотоциклов) с примыкающими к нему боковыми трубчатыми дугами, расширяющими силовую раму до габаритов квадроцикла. Расчеты выявили, что область с пониженными прочностными характеристиками располагается именно в области сопряжения «мотоциклетной» рамы и дополнительных дуг расширения. Для оптимизации конструкции было проведено несколько циклов прочностных экспериментов с варьированием толщины стенки трубчатой конструкции в этой области, а также формы ее крепления к «мотоциклетной» раме. В результате были получены следующие окончательные результаты оптимизации.

Локально возникающее максимальное напряжение растяжения в силовой раме – 333,4 МПа. Эта область отмечена красным. Здесь напряжение не превышает предела прочности для взятого материала (сталь), который составляет 460 МПа, что говорит о правильно выбранном компоновочном решении трубчатых составляющих каркаса конструкции.

В качестве выводов можно отметить, что данная выбранная схема трубчатого каркаса квадроцикла является в достаточной степени адаптивной по своим прочностным характеристикам для принятия в качестве основной в разрабатываемой модели ТС. Однако стоит заметить, что в некоторых локальных областях при статических нагрузках наблюдается незначительное превышения предела текучести, что потребовало введения дополнительных элементов усиления.