Методические рекомендации подготовки к олимпиадам по физике

Школьные олимпиады по физике проводятся в Москве с 1938 года. Первое всесоюзное соревнование прошло в 1962 году. В заключительном этапе ежегодно принимают участие около 300 российских школьников. Станут ли они гениальными учеными – этот вопрос даже в отношении победителей олимпиады по физике остается открытым. Но очевидно – с такими хорошими знаниями в области одной из важнейших естественных наук ребята не пропадут.

В этой статье мы поговорим о методических рекомендациях для учителей по подготовке к олимпиадам и рассмотрим несколько примеров решения задач.

Олимпиадники — неудобная, раздражающая аудитория для непривычного учителя. Их не убеждает звук вашего голоса, они непрерывно ищут у вас ошибки и неточности. И неизбежно их находят, потому что школьный курс физики, втиснутый в рамки образовательных стандартов, всегда содержит недоговоренности, а иногда и неточности. Потенциальный кандидат на участие в олимпиаде по физике всегда задает «неудобные» вопросы, отвечать на которые во время обычного урока бывает некогда.

Олимпиадная задача по физике — это всегда маленькое исследование. Ученику необходимо придумывать модель, которая охватывает основные черты физического явления, описанного в задаче. Он использует физические законы, которым подчиняется модель. Ему приходится задействовать подходящий математический аппарат для нахождения результата. И ему нужно превратить математическую формулу ответа в физическую интерпретацию, в предсказание исхода описанного физического эксперимента или объяснение внутренних причин сюжета задачи. И это уже исследование.

Главный принцип подготовки к олимпиадам изобретен десятилетия назад и очень прост: требуется решать олимпиадные задачи, сравнивать свои решения с авторскими и разбираться, почему возникли ошибки. Роль преподавателя на начальном этапе бесценна - он не только объясняет, где кроются физические парадоксы, но и внушает уверенность, что ошибки — нормальный путь к глубокому пониманию физики.

Многие университетские профессора, академики, понимая важность физических олимпиад, написали чудесные пособия, золотой фонд олимпиадной литературы. Остается только подобрать книгу, подходящую ученику по уровню подготовки. С развитием интернет-технологий подготовка к олимпиадам существенно упростилась — в сети доступны практически любые пособия, авторские видеокурсы, варианты олимпиад разных лет с разобранными решениями.

Вариант работы состоит из двух частей и включает 13 заданий.

Часть 1: содержит 10 заданий с выбором ответа. К каждому заданию приводится четыре варианта ответа, из которых только один правильный.

Часть 2: содержит три задачи открытого типа, для которых необходимо привести развернутый ответ.

Оценивание отдельных заданий и работы в целом.

Задание с выбором ответа считается выполненным, если выбранный участником Олимпиады номер ответа совпадает с верным ответом. Каждое задание части 1 оценивается в 3 балла.

Задания 11-13 оцениваются в 10 баллов каждое, если в задаче приведено развернутое верное решение и получено числовое значение (там, где необходимы расчеты).

Таким образом, максимальный балл за работу составляет 60 баллов.

На выполнение работы учащимся 7-8 классов отводится 1 час, учащимся 9-11 классов - 2 часа.

Для выполнения заданий Олимпиады каждому участнику выдаются чистые двойные листы в клетку (для чистовика и для черновика), а также распечатанный текст заданий.

Участники олимпиады в 7-8 классах вписывают номера правильных ответов к заданиям 1-10 в таблицу, приведенную в тексте работы. К заданиям 11-13 необходимо привести развернутое решение на листочке.

При    выполнении    заданий    допускается    использование непрограммируемого калькулятора.

По окончании работы учащиеся сдают на проверку распечатанные тексты заданий с заполненной таблицей и листы (чистовики и черновики) с решениями заданий открытого типа.

Рассмотрим некоторые задачи второй части олимпиады заданий 11-13:

Задача 1.

Саша, Коля и Дима приняли участие в соревнованиях по бегу на дистанцию L = 200 м. На старте друзья располагались на соседних дорожках. Саша, стартовавший на первой дорожке, финишировал первым через t = 40 с, а Дима на третьей дорожке отстал от победителя на Δt = 10 с. Определите скорость Коли на второй дорожке, если известно, что в момент финиша Саши все три бегуна располагались на одной прямой. Скорости бега спортсменов можно считать постоянными на всей дистанции, а беговую дорожку прямой.

Возможное решение:

Найдём скорость Саши: V1 = L/t и скорость Димы: V3 = L/(t + At)

В момент времени t Дима отстал от Саши на расстояние

Al = (V1 - V3)t.

Из того, что все три друга в этот момент находились на одной прямой, следует, что Коля отстал от Саши на расстояние Δl/2. С другой стороны Δl/2 = (V1 - V2)t, где V2 - скорость Коли. Решая записанную систему уравнений, получим:

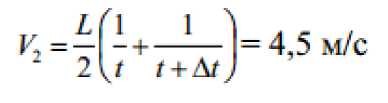
Критерии оценивания:

• •    Найдены скорости Саши и Димы (по 1 баллу за каждую): 2 балла

• •    Найдено расстояние, на которое Дима отстал от Саши в момент времени t: 2 балла

• •    Использовано, что друзья расположены на одной прямой, и получена связь между расстояниями, на которые Дима и Коля отстали от Саши: 2 балла

• •    Записано выражение для расстояния, на которое Коля отстал от Саши в момент времени t, через скорость Коли: 2 балла

• •    Получено выражение для скорости Коли: 1 балл

• •    Получено численное значение скорости Коли: 1 балл

Максимум за задачу – 10 баллов.

Задача 2.

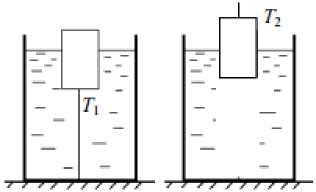
Тело, привязанное нитью ко дну сосуда, погружено в жидкость на 2/3 своего объёма. Сила натяжения нити при этом равна T 1 = 12 Н. Для того чтобы вынуть это тело из жидкости на 2/3 объёма, нужно отвязать тело от дна и приложить к нему сверху направленную вертикально вверх силу T 2 = 9 Н. Определите отношение плотностей жидкости и тела.

Возможное решение:

Запишем условие равновесия тела в первом случае:

Тг + pTVg = Pxg--V ^ ^Р^' Рт) flV = Л где рТ - плотность тела, рЖ - плотность жидкости, □ V- объём тела.

Условие равновесия тела во втором случае:

Тг^РжО--₃V = p_TVg => (р_т "Рж) gV = Т₂

Поделим одно уравнение на другое:

s             _ 3(71+72) _ 7 1

(РтДрж) Т_{2 Л} 1^2 Т₁₊2Г_г •

Критерии оценивания:

• •    Сила Архимеда в виде ρЖ gVпогр: 1 балл

• •    Условие равновесия тела в первом случае : 4 балла

• •    Условие равновесия тела во втором случае : 4 балла

• •    ρЖ/ρT = 2.1: 1 балл

Максимум за задачу – 10 баллов

Готовясь к олимпиадам по физике, нужно помнить о том, что олимпиада – это всего лишь интеллектуальное соревнование, которое проводится, прежде всего, с целью повышения интереса школьников к изучению предмета, а так же на проверку внимательности, так как хорошо прочитанное условие дает возможность не сделать ошибок и правильно решить задачу. Поэтому не следует расстраиваться, если стать победителем олимпиады не удалось. В любом случае подготовка к олимпиаде позволяет глубже освоить школьную программу, изучить дополнительные вопросы курса физики, научиться решать различные типы задач (в том числе, весьма трудных). В конечном итоге, все это принесет ощутимую пользу в плане получения хорошего образования и положительно скажется при сдаче итоговой аттестации в форме ЕГЭ и дополнительных вступительных испытаний при поступлении в Московский университет.