Методические возможности включения темы «Помехоустойчивые коды Рида-Соломона» в образовательный процесс в педагогическом вузе
Автор: Глухова Наталья Владимировна, Сафина Элина Эдуардовна
Журнал: Поволжский педагогический поиск @journal-ppp-ulspu
Рубрика: Математические исследования и образование
Статья в выпуске: 4 (34), 2020 года.
Бесплатный доступ
Целью настоящей работы является демонстрация того, как тема «помехоустойчивое кодирование» может быть использована при обучении будущих учителей математики или информатики. Изучение данного раздела полезно как с точки зрения знакомства будущих учителей с современными методами защиты информации, что важно для учителя информатики, так и с позиции «чистой математики», так как позволяет продемонстрировать прикладную направленность большинства наиболее значимых разделов вузовского курса алгебры. В работе осуществлена попытка восполнения пробелов, имеющихся в литературе по кодам Рида-Соломона и затрудняющих для студентов понимание данного метода защиты информации от ошибок. Рассмотрен конкретный пример составления задач на кодирование и декодирование с нахождением ошибок по методу Рида-Соломона с развернутым (чисто математическим) решением. При этом систематическое кодирование предлагается осуществлять на основе порождающего полинома, а декодирование - при помощи проверочной матрицы, что позволяет избежать некоторых вычислительных сложностей, возникающих при решении задачи без применения электронно-вычислительных средств. Результаты проведенного исследования могут быть использованы для организации внеурочной и проектной деятельности школьников.
Коды рида-соломона, помехоустойчивое кодирование, расширенные конечные поля, преподавание алгебры, расширенный алгоритм евклида, порождающий полином
Короткий адрес: https://sciup.org/142226356
IDR: 142226356 | УДК: 378:519.725:512.6 | DOI: 10.33065/2307-1052-2020-4-34-116-124
Текст научной статьи Методические возможности включения темы «Помехоустойчивые коды Рида-Соломона» в образовательный процесс в педагогическом вузе
Введение. Целью настоящего исследования является рассмотрение возможности и полезности включения вопросов, связанных с теорией кодирования, в процесс подготовки учителей математики и информатики в педагогическом вузе. В частности, методы помехоустойчивого кодирования, которые имеют самое широкое применение в нашей повседневной жизни (так как они предназначены для защиты информации от повреждений), изучаемые во многих технических вузах, редко включается в программы педагогического образования математического профиля. Курс «Элементы абстрактной и компьютерной алгебры», который был включен в образовательные стандарты второго поколения [Матрос 2004: 3, 197; Глухова 2008: 26], предполагал знакомство с основами теории кодирования. К сожалению, такой курс не указывается в качестве обязательного во ФГОС 3 (с его версиями) для педагогического образования. Впрочем, в этих версиях образовательных стандартов вообще отсутствует какое-либо содержательное наполнение предметных профилей.
Для студентов технических вузов тема является весьма сложной. Даже популярные статьи, например, размещенные на сайте habr, призванные помочь разобраться с темой «теория кодирования», которая, по мнению авторов, является самой сложной, изобилуют пропусками и не являются вполне доступными для понимания [Кузмин 2013]. Это связано с тем, что студенты технических вузов не владеют достаточно глубоко математическим аппаратом, необходимым им для полного понимания теоретических основ помехоустойчивого кодирования. Для этого было бы нужно глубокое владение курсами абстрактной теории алгебраических структур, теории чисел, теории многочленов, но они очень в малом объеме изучаются в технических вузах, а такая дисциплины как «теория чисел» даже не упоминается в курсе математики [Сагалович 2010: 4].
В педагогических же вузах классически рассматривают подробно как теорию алгебраических структур, так и теории чисел и многочленов, но студентом не всегда понятно, зачем нужны те или иные разделы этих дисциплин. Чтобы освоить тему «помехоустойчивое кодирование», нужно уметь работать с матрицами и системами линейных уравнений, применять расширенный алгоритм Евклида, который изучается для избавления от иррациональности в знаменателе и для решения уравнений в целых числах в вузовском курсе. Этот алгоритм позволяет находить обратные элементы в конечных полях, а также решать ключевое уравнение для нахождения позиций ошибок. Также полезны знания в области теории групп (классы смежности, циклические группы), колец (сравнимость элементов в кольце по идеалу), теории расширений полей. И, безусловно, необходимо уметь работать с классами вычетов и сравнениями. Все это изучается в рамках стандартного курса математики в педагогических вузах.
Изучение хотя бы в минимальном объеме теории кодирования, хотя бы (и даже, особенно) на математическом уровне (без составления компьютерных программ) могло бы продемонстрировать студентам полезность абстрактных математических знаний в практической деятельности человека. Это в последующем дало бы возможность будущим учителям транслировать ученикам ощущение важности математики, например, во время внеурочной деятельности в рамках таких тем, как «Матрицы», «Алгоритм Евклида», «Теория делимости», а также с помощью организации работы над проектами по тематике теории кодирования. Помимо этого, осознанный подход к изучению дисциплины позволяет подготовить потенциальных квалифицированных преподавателей математики для технических вузов, которые будут в состоянии обращать внимание студентов на необходимые им математические сведения.
В настоящем сообщении мы попытаемся продемонстрировать, как можно решать практические задачи кодирования и декодирования с исправлением ошибок. При этом мы выберем из нескольких различных методов наиболее простые компоненты с тем, чтобы решение этих задачи стало доступным студентам практически без выхода за рамки дисциплин обычного курса математики педагогического вуза: дисциплин «линейная алгебра», «алгебра многочленов», «теория чисел».
Коды Рида-Соломона как метод защиты информации . Коды Рида-Соломона (РС-коды) – это метод помехоустойчивого кодирования (кодирования, позволяющего находить и исправлять ошибки), относятся к группе БЧХ-кодов, впервые были описаны в 1960 году [Reed 1960: 300–304] и в настоящее время находят самое широкое применение в различных сферах, начиная от защиты данных на компакт дисках от царапин, и вплоть до космической связи [Reed 1999: 233–234].
Интерес к построению все новых методов, упрощающих алгоритмы работы с РС-кодами, не ослабевает вплоть до настоящего времени [Квашенников 2020: 37–41, Рацеев 2020: 3–12]. В первую очередь это связано со стремлением ускорить работу данных алгоритмов, что приводит к появлению новых подходов к декодированию, в которых используется все более сложный математический аппарат (быстрое (дискретное) преобразование Фурье [Блейхут 1986: 364, Самсонов 2002: 283], спектральный анализ [Блейхут 1986: 247], теория аппроксимации Паде с рекуррентными соотношениями между определителями Ганкеля [Квашенников 2020: 37]).
Несмотря на большое количество обширных учебников и иных источников по РС-кодам, понимание используемых алгоритмов часто вызывает большие сложности, так как за записями программ и описанием методов ускорения их аппаратной реализации, а также оценками степени вычислительной сложности алгоритма, нередко теряется сама суть метода. Кроме того, алгоритмы требуют выполнения расчетов в полях Галуа. Поэтому для понимания описываемых программ и алгоритмов необходимо владеть способами оперирования с такими элементами. В то же время авторы учебных пособий и научных статей в пояснениях к алгоритмам часто ограничиваются числовыми примерами [Глухова 2008: 29-30, Охорзин 2010: 34-36], либо примерами над простыми (числовыми) полями Галуа GF(p), где р – простое число [Кузмин 2013]. Например, А. Кузмин приводит пример кода над простым полем Галуа и лишь в конце отмечает, что в реальности используются не простые, а расширенные поля [Кузмин 2013]. Как быть в случае расширенных полей, этот автор не поясняет, как, впрочем, и многие другие. Хотя вопросов в этом отношении возникает не мало. Так в учебном пособии Б.Б. Самсонова с соавторами «Теория информации и кодирование» отмечается, что позиции ошибок являются величинами обратными к позициям ошибок и при этом приведены наглядные примеры кодирования с помощью целочисленных матриц, исходя из которых очень хорошо понятно, что в случае, если обратным к корню многочлена является, например, число 2, то и ошибка находится на второй позиции, если 4 – то и ошибка на четвертом месте, и т.п. [Самсонов 2002: 246–247]. Но в случае с расширенными полями Галуа мы имеем дело с такими элементами как а или а2 + 1. Если а2 + 1 - это позиция ошибки,то не так-то просто сразу без дополнительных пояснений понять, где именно она находится, и уж тем более это не ясно, если это лишь элемент обратный к позиции ошибки. Ниже мы попытаемся восполнить указанные пробелы.
Идея систематического помехоустойчивого кодирования базируется на введении некоторой избыточности в сообщение, то есть наряду с k информационными символами вводятся несколько проверочных, так что общая длина передаваемого сообщения (кодового слова) равна n. Такие коды обозначаются (n, k) кодами (количество избыточных символов m = n – k). Для кодов Рида-Соломона используется сокращение РС (n, k).
В книге Лидла и Нидеррайтера представлено полное математическое обоснование теории линейных корректирующих кодов, однако в ней рассматриваются двоичные коды, алфавит которых состоит из 0 и 1 [Лидл 1988:587], в результате чего обнаружение позиции ошибки равносильно ее исправлению (если ошибочен 0, то это 1, а если ошибочна 1, то это 0), поэтому в данной работе не уделяется специального внимания методам расчета величины ошибки. Особенностью (и преимуществом) кодов Рида-Соломона является то, что все вычисления выполняются в рамках двоичного расширенного поля Галуа (это соответствует в действительности применяемым методам работы с байтами, а не с битами, что обеспечивает РС кодам максимальную корректирующую способность [Сагалович 1999: 225, Владимиров 2016: 67]).
Кодирование по методу Рида-Соломона в классических вариантах осуществляется одним из следующих двух способов [Сагалович 1999: 224].
Первый способ основан на применении проверочной и генераторной матрицы, сообщение представляется как вектор, при умножении его на генераторную матрицу вычисляются кодовые слова (передаваемые сообщения), которые затем декодируются с помощью умножения принимающей стороной полученного сообщения на проверочную матрицу. Очень распространено использование в качестве проверочной матрицы усеченной матрицы Вандермонда, Ганкелевых матриц. Вычисление генераторной матрицы для систематического кодирования является более трудоемким процессом [Самсонов 2002: 245].
Второй способ осуществляется путем представления сообщения в виде многочлена, который кодируется путем умножения его на хт (т - количество проверочных символов) с последующим делением на порождающий полином g(x). Прибавляя к полиному информационного сообщения остаток от указанного деления, мы получаем полином, который делится на порождающий полином. Такое свойство обусловлено тем, что действия сложения и вычитания осуществляются в поле Галуа, являющемся расширением поля классов вычетов по модулю два, что делает операции сложения и вычитания в данном поле идентичными. Для декодирования необходимо построение проверочного полинома h(x) степени k, удовлетворяющего условию:
h(x)g(x)≡0(mod (xn+1)) [Владимиров 2016: 66].
Мы предлагаем совместить оба подхода в их наиболее рациональных частях, то есть осуществлять кодирование с помощью порождающего полинома степени dmin-1=n-k=m вида: g(x)=∏(j=0)(m-1)(x+αj ) [Владимиров 2016: 66], корнями которого, очевидно, служат несколько степеней примитивного элемента α выбранного поля Галуа (степень многочлена и количество корней определяется выбранной корректирующей способностью кода). Например, если мы хотим построить код, корректирующий две ошибки, то необходимо добавить к сообщению 4 проверочных символа (два для определения позиции ошибки и два для определения величины ошибки). Тогда необходимо рассмотреть код РС (7, 3). Выберем, для примера, в качестве алфавита поле GF(23), примитивным элементом которого будет корень неприводимого над данным полем многочлена p(x)=x3+x+1 . Обозначим этот корень α. Тогда порождающий полином находится по формуле:
g((73)b=0)(x)=∏(x+αj )=(x+1)(x+α)(x+α2 )(x+α3 )=x4+α2 x3+α5 x2+α5 x+α6
((,), ) (j=0)
Закодируем с помощью данного порождающего полинома информационное сообщение ( α , 1, 0), считая первую координату свободным членом полинома и далее располагая коэффициенты по возрастанию степеней. Многочленом информационного сообщения будет x4 (α+x+0x2 )=x5+αx4 .
Разделим этот полином на порождающий:
|
x5+αx4 |
x4+α2 x3+α5 x2+α5 x+α6 |
|
x5+α2 x4+α5 x3+α5 x2+α6 x |
x+α4 |
α4 x4+α5x3+α5 x2+α6 x
α4 x4+α6x3+α2x2+α2 x+α3
αx3+α3 x2+x+α3=r(x)
х5+ах4+г(х)=х5+ах4+ах3+а.зx2+x+a3 - кодовое слово.
Декодирование же удобно осуществить с помощью матрицы, первая строка которой состоит из 1 (нулевых степеней примитивного элемента α) , вторая строка состоит из степеней альфа в порядке убывания (до нулевой), а все следующие строки являются квадратами, кубами и последующими степенями этой строки. В нашем примере для РС(7, 3) кода в качестве проверочной можно взять матрицу вида
|
f 1 |
1 |
1 |
1 |
1 |
1 |
1 |
^ |
|
1 |
2 |
3 |
4 |
5 |
в |
||
|
a |
a |
a |
a |
a |
a |
||
|
1 |
2 |
4 |
6 |
8 |
0 |
2 |
|
|
a |
a |
a |
a |
a |
a |
||
|
< 1 |
3 |
6 |
9 |
2 |
8 |
||
|
a |
a |
a |
a |
a |
a |
7 |
Данная матрица представляет собой усеченную матрицу Вандермонда, Как легко видеть, умножение на такую матрицу коэффициентов некоторого полинома (от свободного до старшего) соответствует поочередной подстановке в этот полином корней порождающего полинома (которые, как было отмечено выше, совпадают со степенями α ). Поэтому равенство нулю всех результатов такой подстановки эквивалентно, на основании теоремы Безу, делимости многочлена на все линейные множители в разложении порождающего полинома, что в силу их взаимной простоты гарантирует и делимость на сам порождающий полином. Поэтому, если принято правильное сообщение, то остаток от деления его на порождающий полином будет равен нулю, равно как и произведение проверочной матрицы на вектор, составленный из коэффициентов многочлена, являющегося принятым сообщением и записанный в столбец, даст в результате нулевой вектор. Этот факт позволяет объединить оба рассматриваемых подхода к решению задачи декодирования в один.
Т.к. все вычисления производятся в GF(23)), мультипликативная группа которого циклична, все ненулевые элементы поля могут быть получены как степени примитив-
|
ного элемента α , α7=1 . Пользуясь этим фактом можно упростить проверочную матрицу |
||||||||||||
|
i |
1 α |
1 α2 |
1 α3 |
1 α4 |
1 α5 |
α6 = |
/ 1 1 1α |
1 α2 |
1 α3 |
1 α4 |
1 α5 |
1 \ α6 α5 α4 |
|
α2 |
α4 |
α6 |
α8 |
α10 |
α12 |
1 α2 |
α4 |
α6 |
α |
α3 |
||
|
α3 |
α6 |
α9 |
α12 |
α15 |
α18 |
1 α3 |
α6 |
α2 |
α5 |
α |
||
(например, α12 = α7α5 = 1α5 = α5)
Построенный код является систематическим, что, в случае отсутствия ошибок, позволяет очень легко провести процедуру декодирования путем простого отбрасывания проверочных символов. В случае наличия ошибок результат умножения принятого сообщения на проверочную матрицу будет отличаться от нуля, а его коэффициенты дадут полином синдрома S(x).
Многочисленные задачи декодирования преподаватель может легко составить самостоятельно, если будет кодировать некоторое информационное сообщение, а затем произвольно делать любые ошибки в кодовом слове (при этом ошибочными могут быть как информационные, так и проверочные символы). Например, пусть вместо вычисленного ранее кодового слова x5+αx4+αx3+α3 x2+x+α3, , было принято сообщение αx5+x4+αx3+α3 x2+x+α3. Для проверки умножим вектор из его коэффициентов на прове- рочную матрицу
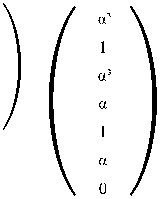
Ненулевой
результат
означает
наличие ошибок, а полином синдрома имеет вид
S(x)=α3 x+α3 x2+α2 x3 .
Дальнейший процесс декодирования состоит в решении ключевого уравнения
S(x)σ(x)+Ф(х) xm= ω(x), которое можно также записать в виде S(x)σ(x)=ω(x)modxm
(известны S(x) и хm, полиномы σ(x), ω(x) требуется найти). Для вычисления полинома локаторов ошибок мы следуем алгоритму, описанному в работе Самсонова [Самсонов 2002: 254–257]: применяется расширенный алгоритм Евклида с выписыванием выражений
R i (x)=a(x) Q i (x)+b(x)P i (x), где a(x)=x m ,b(x)=S(x) и R i (x),P i (x),Q i (x) - возможные значения ω(x),σ(x) и Ф(х). Процесс деления завершается, как только степень выражения в скобках при S(x) станет больше, чем степень остатка.
Сделаем это в нашем примере. x m =x4 , (m = n - k = 4 - количество избыточных символов), синдром S(x)=a3 x+a3 x2+a2 x3 .
д 17 4 4 7 4
х | ax + ax + ax х4 + ах3 + ах2 а5х + а6
«х3 + «х2
ах3 + а2х2 + а2х _________ а4х2 + а2х = /?1(х)
x4=S(x)(a5 x+аб )+Ri (x) . Выразим остаток
Ri (x)=x4-S(x)(a5 x+a6) .
Остаток имеет вторую степень, а многочлен при S(x) – первую, поэтому продолжим процесс деления по алгоритму Евклида
7 4 47 4 I 4 7 7
ах + ах + ax ах + ах а2х3 + х2 а5х + а4
«х2 + а3х
«х2 + а6х а4х = R2to
S(x)=Ri (x)(a5 x+a4 )+R (x)
R2 (x)=S(x)+Ri (x)(a5 x+a4 )=S(x)+(x4+S(x)(a5 x+аб ))(a5 x+a4 )=x4(a5x+a4 )+S(x)(a3 x2+ax+a3+1)
Т.к. степень многочлена, стоящего в скобках рядом с S(x), больше чем степень выражения слева, в этом случае полином в скобках при S(x) является полиномом локаторов ошибок o(x)=a3 x2+ax+a3+1 . Свободный член данного многочлена можно упростить, разделив его на минимальный многочлен для α и заменив на остаток (α3+1= α) , откуда o(x)=a3 x2+ax+a
Вычислив корни данного многочлена (это можно сделать путем простого перебора всех элементов в конечном поле Галуа и последовательной подстановкой их в многочлен), и найдя обратные им, мы получим некоторые элементы поля Галуа, которые можно представить в виде степеней α (примитивный элемент поля). Соответствующие степени переменной в принятом полиноме указывают на позиции ошибочных коэффициентов.
В нашем примере элементов в поле Галуа 8, это 0 и все степени α от первой до седьмой. Подставив х = 0 в многочлен локаторов ошибок, получим α3·0+α·0+α=α≠0 , значит, х = 0 не является корнем; при x=α получим α5+α2+α , поделим его столбиком на минимальный многочлен α3+α+1 , получим что
α5+α2+α = (α3 + α + 1)(α2 + 1) + 1 = 1
(в силу того, что α корень многочлена х3 + х + 1, α3 + α + 1 = 0), поэтому α не является корнем полинома локаторов ошибок. При подстановке x=α2 в полином локаторов ошибок получим α7+α3+α = 1 + α3+α=0, т.е. x=α2 является корнем.
Аналогично находим, что x= α 3 есть корень нашего полинома локаторов (α4+α2+α=α(α3 +α+1)=0), а x=α4, x=α5, х = α6 корнями не являются.
Таким образом, имеется два корня у многочлена локаторов ошибок. Это α 2 и α 3. Найдем обратные к ним, используя соотношение α7=1 . Легко заметить, что α2∙α5=α7 , то есть обратным для α2 является α5 . Аналогично, из отношения α3∙α4=α7 , находим, что ( α3 )-1 является α 4. Следовательно, ошибочны коэффициенты при x5, x4 (в векторном представлении это соответствует пятой и шестой координатам).
Последний остаток до остановки алгоритма Евклида можно принять за полином ошибок (весов) ; он может быть использован для вычисления величин ошибок по методу Форни [Самсонов 2002: 247] . Для решения задачи декодирования в чисто математическом ключе этот метод нам не нужен, так как величины ошибок можно вычислить непосредственно: обозначим произвольными переменными коэффициенты на позициях, в которых были допущены ошибки. Умножим новый вектор с переменными на проверочную матрицу и приравняем результат к нулевому вектору. Решив полученную систему, найдем правильное сообщение.
Так как в нашем примере обозначим ошибочные символы переменными a и b.
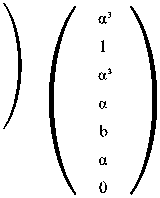
Если сообщение не содержит ошибок, то полученный вектор синдрома должен быть равен 0:
{ а5 а+а4 b=0
α3 a+αb+α5=0
αa+α5 b+α5=0
Решим данную систему способом Гаусса – приведем матрицу системы к ступенчатому виду. Первую строку матрицы умножим на α5 и сложим со второй строкой, также первую строку матрицы умножим на α3 и сложим с третьей строкой. Получим:
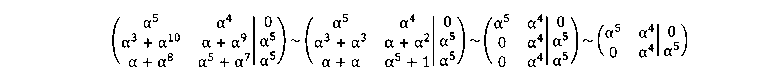
Далее выпишем получившуюся систему уравнений
{ а5 a+а4 b=0 α4 b=α5 .
Отсюда b=α,a=1. Получили x5+αx4+αx3+α3 x2+x+α3 – искомое кодовое слово.
Многочленом информационного сообщения будет x5+αx4 .
Заключение. Таким образом, Коды-Рида Соломона являются достаточно простым и доступным практическим приложением очень большого диапазона теоретических сведений, изучаемых в базовом курсе алгебры. Обучить с их помощью решению задач кодирования и декодирования можно без привлечения сложного математического аппарата. С помощью включения этой темы в учебный процесс в педагогическом вузе можно продемонстрировать практическую полезность сведений из курса теории чисел (таких, как умение находить обратный элемент числа, работать с классами вычетов), из теории многочленов (расширенный алгоритм Евклида, теорема Виета и ряд других), курса линейной алгебры (матрицы, системы линейных уравнений).
К настоящему моменту попытки внедрения данной темы были успешно осуществлены в рамках дисциплины по выбору – «избранные вопросы алгебры», а также при выполнении студентами курсовых проектов. В последние учебные планы 2019 года по профилю «Информатика» были включены дисциплины «компьютерная алгебра» или «компьютерная и абстрактная алгебра». Полагаем, было бы полезным включать эти дисциплины (хотя бы на уровне вариативных курсов) и для студентов математиков. Изучение темы «кодирование» на примере кодов Рида-Соломона позволяет повысить интерес к теоретической математике, закрепить полученные умения и освоить новые понятия «поля Галуа», «алгебраические коды», научится работать с ними на практике.
Список литературы Методические возможности включения темы «Помехоустойчивые коды Рида-Соломона» в образовательный процесс в педагогическом вузе
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986. 576 с.
- Владимиров С. С. Математические основы теории помехоустойчивого кодирования. СПб.: СПбГУТ, 2016. 96 с.
- Глухова Н. В. К вопросу совершенствования обучения теме "Помехоустойчивое кодирование" в курсе "Элементы абстрактной и компьютерной алгебры" // Актуальные вопросы методики обучения математике и информатике. Ульяновск, 2008. Вып. 5. С. 26-31.
- Квашенников В. В. Упрощенный алгоритм декодирования кода Рида- Соломона. Серпухов: Известия института инженерной физики, 2020. № 1 (55). С. 37-41.
- Кузьмин А. Коды Рида-Соломона. Простой пример. [Электронный ресурс]. // URL: https://habr.com/ru/ post/191418/ (дата обращения: 12.08.2020).
- Лидл Р., Нидеррайтер Г. Конечные поля. М.: Мир, 1988. Т. I. 818 с.
- Матрос Д. Ш., Поднебесова Г. Б. Элементы абстрактной и компьютерной алгебры. М.: Академия, 2004. 240 с.
- Охорзин В. М. Построение каскадных кодов на основе кодов Боуза Чоудхури Хоквингема и Рида Соломона. Санкт-Петербург: Теледом, 2010. 56 с.
- Рацеев С. М., Череватенко О. И. О простом алгоритме декодировании кодов БЧХ, кодов Рида-Соломона и кодов Гоппы // Вестник СибГУТИ, 2020. C. 3-14.
- Сагалович Ю. Л. Введение в алгебраические коды. М.: ИППИ РАН, 2010. 302 с.
- Самсонов Б. Б., Плохов Е. М., Филоненков А. И., Кречет Т. В. Теория информации и кодирования. Ростов- на-Дону: Феликс, 2002. 288 с.
- Reed I. S., Chen X. Reed-Solomon Codes. In: Error-Control Coding for Data Networks // The Springer International Series in Engineering and Computer Science. 1999 V. 508. Springer, Boston, MA. Рр. 233-84.
- Reed I. S., Solomon G. Polynomial codes over certain finite fields // SIAM Journal of Applied Mathematics. 1960. Vol. 8. Рр. 300-304.


