Методика агрегированного оценивания систем с поддержкой ключевых компонентов

Построение агрегированных оценок - одно из востребованных направлений современных исследований. Многие управленческие решения принимаются на их основе. Они являются неотъемлемой частью различных методик определения качества продукции, эффективности функционирования социальных и экономических структур, состояния окружающей среды и так далее (см., например, [1-5]). Нередко подобные оценки строятся как различного рода средние: арифметическое, геометрическое, гармоническое, медиана, и имеют иерархический характер: итоговая оценка и оценки промежуточных уровней получаются из оценок нижнего уровня с учётом соответствующей иерархии, причём рост оценки связывают с улучшением качественного состояния системы [1-3].

Составляющие иерархического оценивания часто предполагаются неравноправными: оценки нижних уровней иерархии вносят разный вклад в промежуточные и итоговую оценки. Это обстоятельство обычно учитывается весами начальных и промежуточных оценок и от простых средних переходят к взвешенным средним. Однако подобное оценивание обладает определёнными недостатками.

Во-первых, при достаточно развитой иерархии оценки нижних уровней иерархии слабо влияют на общую оценку. Изменение какой-либо оценки начального уровня практически не сказывается на итоге (на это было обращено внимание, например, в [6]).

Во-вторых, с его помощью невозможностью учесть такую особенность как ключевые компоненты (подсистемы, функциональные элементы) в системе. Под ключевым здесь понимается компонент, утрата которого обесценивает соответствующую подсистему или систему в целом. «Обесценивание» здесь означает, что агрегированная оценка принимает своё наименьшее значение, например ноль. Действительно, независимо от значений весовых коэффициентов α(Ci, S), обнуление любого из слагаемых, например, при средневзвешенном оценивании:

n ( S )

£ a ( C i , S ) x ( C i)

X ( S ) =

i = 1

n ( S )

£ a ( C i , S )

i = 1

не обеспечивает нулевого значения χ ( S ) при отдельно взятом χ ( C i ) = 0. Здесь χ ( S ), χ ( C i ) -оценки системы S и компонента C i соответственно, α ( C i , S ) - вес (ценность) компонента C i для системы S , n ( S ) - число компонентов C i в системе S (считаем, что χ = 0 означает утрату, обесценивание соответствующего компонента или системы). Агрегирование при помощи средних геометрических или средних гармонических (включая взвешенные), наоборот, приводит к тому, что все компоненты становятся «ключевыми». Несколько сложнее ситуация с медианным оцениванием, однако и здесь при наличии трёх и более компонентов в системе или подсистеме эффективный учёт ключевых компонентов практически невозможен (медиана получит нулевое значение только если более половины компонентов будут охарактеризованы числом 0).

Наконец, в-третьих, при известных способах агрегирования обычно учитываются только иерархические связи между компонентами (вхождение функционального элемента в подсистему, подсистемы в систему, причём обычно с непересекающимися ветвями иерархий), но не влияние компонентов друг на друга, когда утрата функциональности одного из них влечёт снижение или утрату функциональности другого.

Очевидно, что если влияние компонентов друг на друга существенно и в системе имеются ключевые компоненты, подобные способы агрегирования оказываются неподходящими. Возникает задача разработки методики оценивания, учитывающей эти особенности. Причём методика должна позволять назначать эти компоненты выборочно, в соответствии с особенностями системы.

1    Агрегированное оценивание с поддержкой ключевых компонентов

В работе [7] предложен логико-аксиологический подход к оценке эффективности систем.

В его основу положено следующее.

• I .    Система S считается состоящей из компонентов C i , в качестве которых рассматриваем подсистемы и функциональные элементы; компоненты-подсистемы в свою очередь также могут содержать свои собственные компоненты. Здесь i - индекс компонента; количество компонентов на каждом уровне иерархии считаем конечным.

• II .    Состояние системы в целом и каждого из её компонентов характеризуется числами χ ( S ), χ ( C i ) ∈ [0, 1] (характеризующие числа), где 0 означает утрату системы (компонента), неисполнение системой или компонентом своих целевых задач, а 1- полноценное функционирование.

• III .    С каждым компонентом C также связаны одно или несколько чисел а ( C , С ‘ ) е [0, 1], называемых ценностью C для C ′ ; α ( C , С ′ ) показывает на сколько уменьшается характеризующее число χ (C ′ ) при утрате компонента C (когда χ ( C ) = 0). В качестве C ′ выступают те компоненты системы, характеризующие числа которых зависят от C . Это может быть систе-

• ма/подсистема, содержащая C в качестве своего непосредственного компонента, или другой компонент, на состояние которого C оказывает непосредственное влияние.

• IV .    Вводится понятие ключевого компонента . Компонент C является ключевым для C ′ , если χ ( C ) = 0 влечёт χ ( C ′ ) = 0. Если C ключевой для C ′ , то α ( C , С ′ ) = 1.

• V .    Убыль эффективности компонента C ′ при частичной утрате компонентом C своих функциональных возможностей рассчитывается как:

• (1)                               ∆ ( C ′ ) = α ( C , С ′ ) ⋅ ∆ ( C ),

где ∆ ( C ′ ) = 1 - χ ( C ′ ) и ∆ ( C ) = 1 - χ ( C ).

• VI . Если состояние компонента C ′ зависит от состояний компонентов C 1 , C 2 , …, C n :

• (2)                                 ∆ 1 ( C ′ ) = α ( C 1 , С ′ ) ⋅ ∆ ( C 1 );

• (3)                                 ∆ 2 ( C ′ ) = α ( C 2 , С ′ ) ⋅ ∆ ( C 2 );

• (4)                                 ∆ n ( C ′ ) = α ( C n , С ′ ) ⋅ ∆ ( C n ).

∆ i ( C ′ ) - это частичные утраты функциональности компонента C ′ , обусловленные частичной утратой (снижением качества, снижением функциональности и т.д.) компонентов C i . Для расчёта результирующего значения ∆ ( C ′ ) воспользуемся некоторой функцией u ( ∆ 1 ( С ′ ),…, ∆ n ( С ′ )) со свойствами:

• (5)                            ∀ i ( ∆ i = 0) ⇔ u ( ∆ 1 ,…, ∆ n ) = 0;

• (6)                              ∃ i ( ∆ i = 1) ⇒ u ( ∆ 1 , …, ∆ n ) = 1;

• (7)                            ∀ i (¹ ∆ i ≤ ² ∆ i ⇒ u (…,¹ ∆ i , …) ≤ u (…,² ∆ i , …)).

(здесь и далее для краткости используем обозначения ∆ i ( C ′ ) = ∆ i , χ i ( C ′ ) = χ i , α ( C i , С ′ ) = α i , ∆ ( C ′ ) = ∆ , χ ( C ′ ) = χ ).

Принимая во внимание связи ∆ i = 1 - χ i и ∆ ( C i ) = 1 - χ ( C i ), выражения для (2)-(4) можно переписать относительно χ ( C i ):

χ 1 = 1 - α 1 ⋅ (1 - χ ( C 1 ));

χ 2 = 1 - α 2 ⋅ (1 - χ ( C 2 ));

χ n = 1 - α n ⋅ (1 - χ ( C n )).

И результирующее значение χ рассчитывать с использованием функции v ( χ 1 ,…, χ n ), со свойствами:

• (8)                              ∀ i ( χ i = 1) ⇔ v ( χ 1 ,…, χ n ) = 1;

• (9)                              ∃ i ( χ i = 0) ⇒ v ( χ 1 ,…, χ n ) = 0;

• (10)                            ∀ i (¹ χ i ≥ ² χ i ⇒ v (…,¹ χ i , …) ≥ v (…,² χ i , …)).

Свойства (5) и (8) означают, что C ′ полноценно функционирует если и только если полноценно функционируют все влияющие на него компоненты C i ; (6) и (9), - что утрата ключевого компонента (когда ∆ i = 1) влечёт утрату C ′ ; (7) и (10), - что ущерб для C ′ монотонно возрастает с ростом ∆ i , а функциональность C ′ падает с падением функциональности влияющих на него компонентов.

Кроме того отметим, что поскольку между χ ( C i ) и ∆ ( C i ), а также χ i и ∆ i существует взаимосвязь χ ( C i ) + ∆ ( C i ) = 1 и χ i + ∆ i = 1, её естественно требовать и для пары агрегированных показателей χ и ∆ . Это влечёт равенство:

• (11)                            u ( ∆ 1 ,…, ∆ n ) + v ( χ 1 ,…, χ n ) = 1.

Пары функций u (…) и v (…) будем называть сопряженными. Примерами таких пар являются:

u ( A 1 , A 2 ,..., A n ) = max ( A 1 , A 2 ,..., A n );

u ( A i , A 2 ,_, A n ) = 1 - П ( 1 -A, ) ;

i = 1

u ( A i , A 2 ,_, A n ) = min( 1 , g A , ) ;

i = 1

v ( X 1 , X 2 ,-, X n ) = ^mi^{n (} X 1 , X 2 ,^, X n );

• v ( χ 1 , χ 2 ,…, χ n ) = ∏ ⁿ χ _i ;

i = 1

• V ( X 1 , % 2 ,^, X n ) = max( 0 , ^gX , — 1 ) ;

i = 1

n

u ( A A 2 ,_, A n ) = 1 - n П ( 1 — A , ) ;

n

α i n

u( A 1 , A 2 ,_, A n ) = 1 - П ( 1 — A , -) g ° - ;

i = 1

Первые три группы функций связаны с понятиями

n

v ( χ 1 , χ 2 ,…, χ n ) = n ∏ χ _i ;

α i

n n

v ( χ 1 , χ 2 ,…, χ n ) = ∏ χ _i ∑ _{i = 1} ^α i .

i = 1

триангулированной ко-нормы и триангу-

лированной нормы, известными из нечёткой логики и теории нечётких множеств [8]. Четвёртая и пятая – среднее геометрическое и среднее геометрическое взвешенное, используемые в квалиметрии [1, 9]. Этим список функций не исчерпывается.

Компоненты C i , связанные с C ′ , выступают в двух качествах: как структурные компоненты, образующие C ′ (если C ′ – это сама система S , то структурные компоненты есть образующие S подсистемы и функциональные компоненты первого уровня иерархии), и (возможно) как компоненты влияния. Под последними понимаем компоненты, не входящие в состав C ′ , но влияющие на его функционирование (рисунок 1). Их принципиально различает то, что утрата любого количества компонентов влияния (если только среди них нет ключевых) не влечёт утраты C ′ , тогда как утрата всех структурных компонентов влечёт утрату C ′ , даже если они не ключевые. С целью учёта такой особенности структурных компонентов, для расчёта результирующих значений ∆ ( C ′ ) и χ ( C ′ ) при изменении χ ( C i ) структурных компонентов используем полученные на основе u (…) и v (…) функции:

U ( ∆ 1 ,…, ∆ n ) =

u ( A 1 ,..., A n ) ; u ( a ₁ ,..., a n ) ’

V ( χ 1 , …, χ n ) =

V ⁽ X 1 ,-, X n ) ^- V ^{( 1 - a} 1 ^,-, ^{1 - a} n )

1 - v ( 1 - a ₁ ,..., 1 - a n )

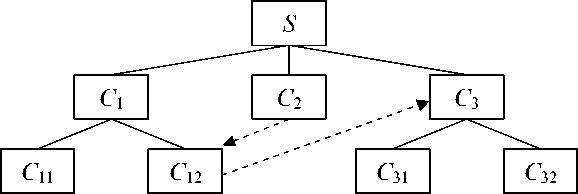
структурный компонент (отношение «состоит из»);

компонент влияния (отношение «влияет на»)

Рисунок 1 – К понятиям структурного компонента и компонента влияния

Функции U (…) и V (…) имеют свойства, аналогичные функциям u (…) и v (…):

• (14)       ∀ i ( ∆ i = 0) ⇔ U ( ∆ 1 ,…, ∆ n ) = 0;      ∀ i ( χ i = 1) ⇔ V ( χ 1 ,…, χ n ) = 1;

• (15)       ∃ i ( ∆ i = 1) ⇒ U ( ∆ 1 ,…, ∆ n ) = 1;        ∃ i ( χ i = 0) ⇒ V ( ∆ 1 ,…, ∆ n ) = 0;

∀ i (¹ ∆ i ≤ ² ∆ i ⇒ U (…,¹ ∆ i , …) ≤ U (…,² ∆ i , …));

∀ i (¹ χ i ≥ ² χ ⇒ V (…,¹ χ i , …) ≥ V (…,² χ i , …)).

Они следуют из определений U (…) и V (…) и свойств функций u (…) и v (…): (5) и (8) - для (14), (6) и (9) - для (15). При этом в (14) учтено, что в силу зависимостей ∆ i = α i ⋅ ∆ ( C i ) и ∆ i + χ i = 1, равенства ∆ i = 1 и χ i = 0 реализуются, если и только если α i = 1. Плюс к этим трём свойствам, повторяющим свойства функций u (…) и v (…), добавляется ещё:

U ( α 1 ,…, α n ) = 1;

• V (1 - α 1 ,…, 1 - α n ) = 0.

Это обеспечивает правильные значения ∆ и χ при утрате всех структурных компонентов. Наконец, можно удостовериться и в справедливости свойства:

U(∆1,…, ∆n) + V(χ1,…, χn) = 1, которое вытекает из (11) и того факта, что u(α1,…, αn) = 1 - v(1-α1,…, 1-αn).

Отметим также, что если u ( α 1 ,…, α n ) = 1, то U ( ∆ 1 ,…, ∆ n ) = u ( ∆ 1 , …, ∆ n ), и V ( χ 1 , …, χ n ) = v ( χ 1 ,…, χ n ). Первое равенство очевидно, второе следует из первого, из определения V (…) и из (11).

• VII . Для получения итоговых ∆ и χ используем сначала функции U (…) и V (…) для учёта вкладов структурных компонентов, затем функции u (…) и v (…) для учёта вкладов компонентов влияния.

2    Логико-аксиологический подход к агрегированному оцениванию

Вышеприведённая методика эффективно реализуется как логический вывод на основе технологии экспертных систем (ЭС). Это позволяет разработать достаточно универсальную оценивающую программу, в которой впоследствии придётся менять только базу знаний, описывающую конкретную систему, и вид функций u (…) и v (…), если это необходимо. В основе реализации лежит аналогия между этапами вышеописанного агрегированного оценивания и присоединённым логическим выводом, использующим нечёткую логику.

Считаем χ истинностью суждения «Компонент C ′ эффективен», а ∆ - суждения «Компонент C ′ не эффективен», которые будем обозначать как c ′ и c ′ . Обозначая истинность произвольного суждения a как || a ||, можно записать: || c ′ || = χ и || c ′ || = ∆ . Аналогично:

||«Компонент C i эффективен»|| = || c i || = χ ( С i );

||«Компонент C i не эффективен»|| = || c i || = ∆ ( С i ).

Ценность α ( C i , С ′ ) свяжем с истинностью суждения:

|| c i → c ′ || = α ( C i , С ′ ).

С учётом этого агрегирование по схеме (2)-(4) с последующим объединением частичных убылей эффективности и с использованием функций U и u выглядит как логический вывод по схеме:

c 1 , c 1 → c ′ ├ c ′ : || c ′ || 1 = || c 1 || ⋅ || c 1 → c ′ ||;

cn, cn→c′├ c′: ||c′||n = ||cn||⋅||cn → c′|| c′: ||c′|| = ∪(||c′||1,… , ||c′||n);

где ∪ (|| c ′ || 1 ,… , || c ′ || n ) = U (|| c ′ || 1 ,… , || c ′ || n ) для структурных компонентов и ∪ (|| c ′ || 1 , … , || c ′ || n ) = u (|| c ′ || 1 , … , || c ′ || n ) для компонентов влияния. Это присоединённый вывод по правилу modus ponens ; через двоеточие указана схема расчёта истинности заключения по истинности посылок.

Предлагаемый подход пригоден для учёта не только положительного, но и отрицательного вклада компонентов в функционирование C ′ , когда C i «подавляет» C ′ . Формально это можно выразить равенством

• (16)                               ∆ i ( C ′ ) = α ( C i , С ′ ) ⋅ χ ( C i ),

или импликацией ci → c′, и шагом вывода ci, ci → c′├ c′: ||c′||i = ||ci||⋅||ci → c′|| в логической форме. Функции U(…) и V(…), обрабатывающие компоненты структуры, при этом сохраняются, с той особенностью, что в выражениях u(α1,…, αn) и v(1-α1,…, 1-αn), не учитывается вклад структурных компонентов, отрицательно влияющих на C′ (назовём их «паразитными»). В этом можно убедиться, заметив, что u(α1,…, αn) и v(1-α1,…, 1-αn) - это значения функций u(…) и v(…) при всех χ(Ci) = 0 (утрата всех компонентов структуры соответствующего C′). Но в силу (16), соответствующие ∆i(C′) в этом случае равны 0.

Цепочка вывода выстраивается так, чтобы учесть особенности («последовательность») взаимодействия компонентов.

3    Примеры

В завершение продемонстрируем описанную методику на двух примерах.

Пусть компоненты C 1 , C 2 , C 3 на рисунке 1 имеют ценности α 1 = 0.5, α 2 = 0.6, α 3 = 0.7 для S (т.е. в качестве C ′ выступает сама система); C 11 , C 12 имеют ценности α 11 = 0.8, α 12 = 0.9 для C 1 ; C 31 , C 32 - ценности α 31 = 0.9, α 32 = 0.5 для C 3 , причём компонент C 32 паразитный. Компонентами влияния выступают C 2 , влияющий негативно с силой α 2-12 = 0.3 на C 12 и компонент C 12 , влияющий с силой α 12-3 = 0.7 на C 3 . Характеризующие числа компонентов χ ( C 11 ), χ ( C 12 ), χ ( C 2 ), χ ( C 31 ), χ ( C 32 ) все примем равными 0.6.

Соответствующий вывод выглядит следующим образом. Сначала инициируются значения истинности стартовых компонентов:

• 1)    χ ( C 11 ) = || с 11 || = 0.6;

• 2)    χ ( C 12 ) = || с 12 || = 0.6;

• 3)    χ ( C 2 ) = || с 2 || = 0.6;

• 4)    χ ( C 31 ) = || с 31 || = 0.6;

• 5)    χ ( C 32 ) = || с 32 || = 0.6.

Далее, поскольку есть влияние на стартовые компоненты (здесь - C 2 на C 12 ), вносим коррективы в || с 12 ||:

• 6)    c 2 , c 2 → c 12 ├ c 12 : || c 12 || 2 = || c 2 || ⋅ || c 2 → c 12 || = || с 2 || ⋅ α 2-12 = 0.6 ⋅ 0.3 = 0.18;

• 7)    || c 12 || = u (0.4, 0.18) = 0.4 + 0.18 - 0.4 ⋅ 0.18 = 0.508 - объединяем введённую истинность || с 12 || = 0.4 с вычисленным только что вкладом негативного компонента влияния с 2 ; в качестве u (…) здесь и далее возьмем (12).

Рассчитаем ∆ 1 :

• 8)     c 11 , c 11 → c 1 ├ c 1 : || c 1 || 1 = || c 11 || ⋅ || c 11 → c 1 || = || с 11 || ⋅ α 11 = 0.4 ⋅ 0.8 = 0.32;

• 9)     c 12 , c 12 → c 1 ├ c 1 : || c 1 || 2 = || c 12 || ⋅ || c 12 → c 1 || = || с 12 || ⋅ α 12 =0.508 ⋅ 0.9 = 0.4572;

  10) ∆ 1 = || c 1 || =

  
  

  u (0.32,0.4572) 0.32 + 0.4572 - 0.32 ⋅ 0.4572

  =                           ≅ 0.6438

  
  

  u (0.8,0.9)

  
  

  0.8 + 0.9 - 0.8 ⋅ 0.9

  
  

  - здесь учтено, что c 11 и

  
  

c 12 - компоненты структуры для c 1 .

Рассчитаем ∆ 3 по известным || с 31 || и || с 32 ||, учитывая, что с 32 - «паразитный» компонент:

• 11)     c 31 , c 31 → c 3 ├ c 3 : || c 3 || 1 = || c 31 || ⋅ || c 31 → c 3 || = || с 31 || ⋅ α 31 =0.4 ⋅ 0.9 = 0.36;

• 12)    c 32 , c 32 → c 3 ├ c 3 : || c 3 || 2 = || c 32 || ⋅ || c 32 → c 3 || = || с 32 || ⋅ α 32 =0.6 ⋅ 0.5 = 0.3;

  • 13)    ∆ 3 = || c 3 || =

  
  

  u (0.36,0.3)    0.36 + 0.3 - 0.36 ⋅ 0.3

  =                     ≅ 0.6133.

  
  

  u (0.9)

  
  

  0.9

  
  

  Учитываем влияние C 12 на C 3 :

  • 14)     c 12 , c 12 → c 3 ├ c 3 : || c 3 || 3 = || c 12 || ⋅ || c 12 → c 3 || = || с 12 || ⋅ α 12-3 = 0.508 ⋅ 0.7 = 0.3556;

  • 15)    || c 3 || ≅ u (0.6133, 0.3556) = 0.6133 + 0.3556 - 0.6133 ⋅ 0.3556 ≅ 0.7508.

  Наконец, рассчитаем ∆ , выполнив необходимые шаги вывода:

  
  

  16) c 1 , c 1 → s ├ s : || s || 1 = || c 1 || ⋅ || c 1 →

  
  

  17) c 2 , c 2 → s

  18) c 3 , c 3 → s

  
  

  ├ s : || s || 2 = || c 2 || ⋅ || c 2 → ├ s : || s || 3 = || c 3 || ⋅ || c 3 →

  
  

  s || ≅ 0.6438 ⋅ 0.5 = 0.3219;

  s || = 0.4 ⋅ 0.6 = 0.24;

  s || ≅ 0.7508 ⋅ 0.7 ≅ 0.5256;

  
  

  • 19)    ∆ = || s || ≅

  
  

  u (0.3219,0.24,0.5256) 1 - (1 - 0.3219) ⋅ (1 - 0.24) ⋅ (1 - 0.5256)

  =                                    ≅ 0.8037.

  
  

  u (0.5,0.6,0.7)

  
  

  1 - (1 - 0.5) ⋅ (1 - 0.6) ⋅ (1 - 0.7)

  
  

Окончательно:

• 20)    χ = || s || = 1 - || s || ≅ 0.1963.

Всю эту цепочку выполняет машина вывода ЭС.

При отсутствии отношений влияния C 2 на C 12 и C 12 на C 3 (см. рисунок 1), а также «непа-разитности» структурного компонента C 32 , получаем обычную иерархию и довольно простой логический вывод:

|| с 11 || = 0.6;

|| с 12 || = 0.6;

|| с 2 || = 0.6;

|| с 31 || = 0.6;

|| с 32 || = 0.6;

c 11 , c 11 → c 1 ├ c 1 : || c 1 || 1 = || c 11 || ⋅ || c 11 → c 1 || = || с 11 || ⋅ α 11 = 0.4 ⋅ 0.8 = 0.32;

c 12 , c 12 → c 1 ├ c 1 : || c 1 || 2 = || c 12 || ⋅ || c 12 → c 1 || = || с 12 || ⋅ α 12 =0.4 ⋅ 0.9 = 0.36;

∆ 1 = || c 1 || =

u (0.32,0.36) ₌ 0.32 + 0.36 - 0.32 ⋅ 0.36

u (0.8,0.9)

0.8 + 0.9 - 0.8 ⋅ 0.9

≅ 0.5763;

c 3 || = || с 31 || ⋅ α 31 = 0.4 ⋅ 0.9 = 0.36;

c 3 || = || с 32 || ⋅ α 32 =0.4 ⋅ 0.5 = 0.2;

c 31 , c 31 → c 3 ├ c 3 : || c 3 || 1 = || c 31 || ⋅ || c 31 →

10) c 32 , c 32 → c 3 ├ c 3 : || c 3 || 2 = || c 32 || ⋅ || c 32 →

11) ∆ = || c || = ^{u (0.36,0.2)} = ^{0.36 + 0.2 - 0.36 ⋅ 0.2} ≅ 0.5137;

• ^{3       3}      u (0.9,0.5)     0.9 + 0.5 - 0.9 ⋅ 0.5

  12) c 1 , c 1 → s ├ s : || s || 1 = || c 1 || ⋅ || c 1 →

  
  

  • 13)     c 2 , c 2 → s

  • 14)     c 3 , c 3 → s

  
  

  • 15)    ∆ = || s || ≅

  
  
  
  
  
  

  ’s : || s || 2 = || c 2 || ⋅ || c 2 → ’s : || s || 3 = || c 3 || ⋅ || c 3 →

  
  

  s || ≅ 0.5763 ⋅ 0.5 ≅ 0.2882;

  s || = 0.4 ⋅ 0.6 = 0.24;

  s || ≅ 0.5137 ⋅ 0.7 ≅ 0.3596;

  
  

  u (0.2882,0.24,0.3596) 1 - (1 - 0.2882) ⋅ (1 - 0.24) ⋅ (1 - 0.3596)

  =                                    ≅ 0.6953.

  
  

  u (0.5,0.6,0.7)

  
  

  1 - (1 - 0.5) ⋅ (1 - 0.6) ⋅ (1 - 0.7)

  
  

Окончательно:

16) χ = || s || = 1 - || s || ≅ 0.3047.

Если объявить компонент С 32 ключевым для С 3 ( α 32 = 1), и компонент С 3 ключевым для S ( α 3 = 1) расчёт по приведённой схеме при χ ( С 32 ) = || c 32 || = 0 даст значение χ = || s || = 0. В полном соответствии с представлением о ключевом компоненте.

Заметим, что выбор функции объединения u (…) - отдельная задача. От неё во многом зависит результат оценивания. Например, если в последнем примере в качестве функции u (…) взять (13) - среднее геометрическое используется в проблеме оценки качества, - получаем χ ≅ 0.62. В общем случае выбор u (…) и v (…) диктуется предметной областью. Причем, в пределах одной системы различные её компоненты могут требовать разные функции объединения. Пример дан в [7].

Заключение

Таким образом, можно заключить, что предлагаемая методика позволяет учитывать вклад ключевых компонентов в агрегированные оценки систем различной природы и может быть программно реализована на основе технологии ЭС. Последнее избавляет специалистов от необходимости разрабатывать алгоритмы и компьютерные программы оценивания отдельных систем, заменяя программирование описанием внутрисистемных взаимосвязей в виде базы знаний.

Получаемая оценка зависит от структуры системы, значений ценностей компонентов и вида функций объединения, которые определяются предметной областью и могут различаться в пределах одной системы. Выбор функции ∪ (…) - отдельная задача, требующая специальных исследований.

Представленная методика не претендует на полноценное количественное моделирование влияния компонентов системы на её состояние, однако качественное описание, включая учёт роли ключевых компонентов, она обеспечивает.