Методика численного расчёта газодинамических характеристик струйных элементов пневмоавтоматики систем управления сложными техническими системами

внутри каналов струйных устройств проведено методом конечных объёмов, базирующимся на численном решении систем дифференциальных уравнений в частных производных Навье-Стокса, осреднённых по методу Рейнольдса. Уравнения Навье-Стокса включает уравнение сохранения массы (уравнение неразрывности), уравнение сохранения количества движения и уравнение сохранения энергии. Данный метод реализуется с помощью программного комплекса ANSYS CFX. Для замыкания этих уравнений применяется модель турбулентности, сформулированная в соответствии с предположением Буссинеска, согласно которому рейнольдсовы напряжения могут быть связаны со скоростью средней деформации через турбулентную вязкость.

Уравнение неразрывности записывается в виде:

вр  . j о.

д1    дxt'

Уравнение сохранения количества движения [5, 6]:

Р ;. ' ; puUj p-P+ о tx        дхЛдx.

д

+ —5 M eff дx.

(д U_t   д U ) 2 д U _c

+ j M ff‘-

^ дxi    дxi J 3 # дxi для i = 1,2,3.

Проекции U _i и U_j соответствуют компонентам U_x , U_y , U_z вектора скорости потока; p - плотность; 5 _tj - символ Кронекера. Параметр P ^* представляет собой сумму давления

P и величины ( 2/3 ) pS ij k , где k — турбулентная кинетическая энергия. Оба этих слагаемых соответствуют нормальным напряжениям. Эффективная вязкость M ef определяется суммой ламинарной и турбулентной вязкостей

M eff = M + M t . Уравнение сохранения энергии представляется следующим образом:

I ( PH ^)-

( PU j H )

5P  9

+--

5 t   9x i

a f, а т   Mt ah'

---- Л--1---

5 x j ^ 9x j   Pr t 9x j _у

+---x

9x j

5 k   _т т   ^f d U i   d Uj  2 9 U, Л

M--+ UMeff--+-----5j

9xj         ^ 9xj   9xj   3 9xj   у где H = h + 0,5UUj + k - полная энтальпия; h – энтальпия; T – температура; Prt – турбулентное число Прандтля. Также в систему уравнений включено уравнение состояния. Во всех уравнениях по повторяющимся индексам производится суммирование [7, 8]. Для замыкания уравнений неразрывности, сохранения количества движения и сохранения энергии в исследованиях настоящей работы использовалась гибридная двухзональная модель Ментера (модель переноса сдвиговых напряжений) [9].

Уравнения переноса для характеристик турбулентности в соответствии с гибридной двухзональной моделью турбулентности Ментера (SST) имеют вид [10]:

I" ⁽ P k )⁺^ ⁽ P k^U i ) =

9 1 9 x i

*          9

=Pk — вPtok + — dxi x 9 k

⁺ ° k M t )— d x i

—( pto ) +— ( pto U ) = ap S ² - ppto ² +—x

9 t         9 x i                              9 x j

+ 2(1 — F ) PG 2 ⁵ k 9to to       9 x j 9 x j

,            х 9to

( M ⁺ M t ^G to ) — 9 x j

В уравнении переноса для k функция P_k , используемая в модели SST для предотвращения нарастания турбулентности в застойных областях, записывается следующим образом [11]: P_k = min( P_k ,10 • D_k ) , где D_k = в p k to , to -скорость диссипации кинетической энергии, в = 0,09 . В двузональной модели Ментера применяются две системы констант, составляющие которых отмечены индексами 1 и 2:

G k 1 = 0,85; G to _X = 0,5; р _х = 4^; а _х = 9;

_CT k 2 = 1; G_{to 2} = 0,856; в ₂ = 0,0828; а ₂ = 0,44.

Первая система калибрована по пристеночным течениям, а вторая обладает высокой степенью применения для свободных сдвиговых слоёв. Первая система констант используется во внутренней области пограничного слоя и соответствует k — to модели Уилкокса, а вторая – в области пограничного слоя и соответствует стандартной k — £ модели. В модели Ментера используется линейная комбинация этих двух систем констант с гладким переключателем вида ф = Р_хф_х + (1 — Р_х')ф₂ , где F 1 - связующая функция. Вблизи стенки в значительной части пограничного слоя эта функция должна быть близка к единице. Однако, по мере перехода от стенки и приближения к границе пограничного слоя она стремится к нулю, чтобы обеспечить независимость от внешних условий, характерную для k — £ модели. Связующая функция определяется по формуле:

F = th(arg 4 ) ;

f ^   500 v )

arg 1 = min

max

( 0,09 to y’ y ² to у CD_k to y ²

f

^CD k to = ^{max 2} P^G to 2

I

1 9 k 9to to 9 x j 9 x j ’

где arg 1 - переменная, CD_{k to} - положительная часть перекрёстных диффузионных членов в уравнении переноса.

По мере удаления от стенки arg1 ^ 0. Внутри пограничного слоя первый член представляет отношение масштаба турбулентности к расстоянию от стенки и равен 2,5 в логарифмическом подслое. Он исчезает при приближении к границе подслоя. Второй член записан так, чтобы F1 =1 в пределах подслоя (когда исключается использование двухпараметрической диссипативной модели турбулентности). При этом параметр 1/угю является константой вблизи стенки, но в логарифмической зоне он стремится к нулю. Третий аргумент в формуле пере- менной arg1 предотвращает вырожденность решения исходной модели k — to при малых значениях to набегающего потока.

В целях наилучшего моделирования ограниченных стенками потоков, в отличие от модели k — to, в модель SST введена расширенная формулировка вихревой вязкости a1k vt =-------------, где вместо абсолютной max(ax to, SF)

величины завихренности потока Q , применяемой в ранних версиях модели Ментера, используется абсолютная величина скорости сдвиговых деформаций S = (2 S ij S ij )^1/2 .

Функция F₂ имеет вид:

F 2 = tli(arg 2 );

Г    kk   500 v )

arg2 = max 2------,—— ,

2      ( 0,09 my y2to J где arg2 – переменная. Для внешнего слоя константы не изменяются, а для внутреннего слоя добавляется константа a1=0,31.

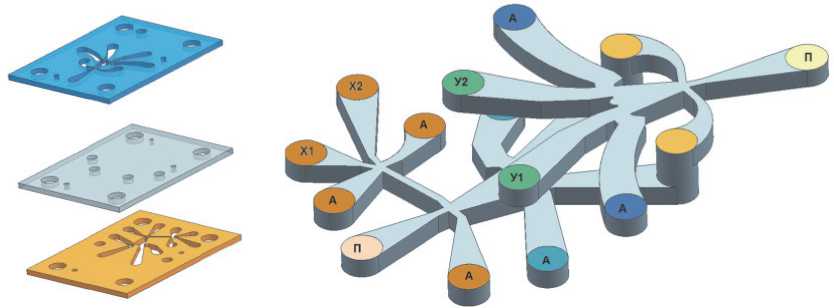
На основе описанных математических моделей проведён расчёт газодинамических характеристик струйного двухвходового усилителя, трёхмерная геометрическая модель которого представлена на рис. 1. На рис. 2 изображён общий вид расчётной сетки. Для моделирования вязкого взаимодействия стенки каналов и газа предусмотрен градиентный рост толщины ячеек с поверхности канала.

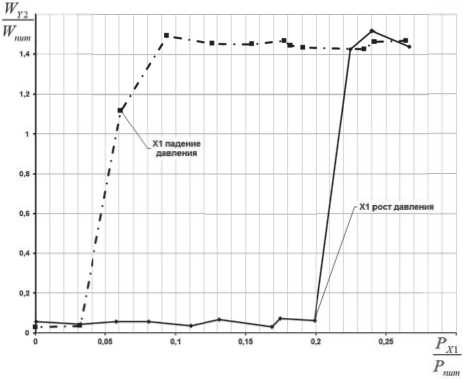
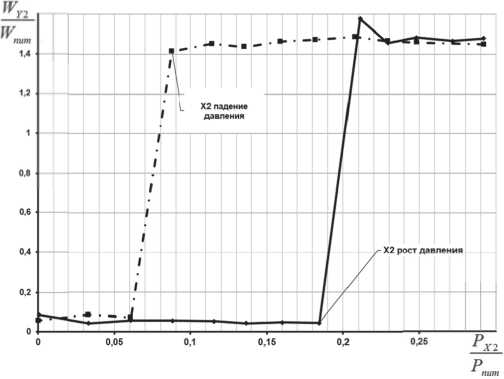
На входах в каналы питания задана величина скорости потока. Скорость на входе в канал питания нижней платы струйного двухвходового усилителя равна 16,5 м/с, а на входе в канал питания верхней платы 14,5 м/с. Величины скоростей подобраны таким образом, чтобы дав- ление газа на входе в каналы питания соответствовало заданной величине 20 кПа.

Управляющие сигналы, поступающие на нижнюю плату устройства, моделируются граничным условием скорость на входе. Величина скорости потока на входе в управляющие каналы переменная и подбирается из условия соответствия давления газа в канале заданному диапазону. Необходимость перехода от давления к скорости потока при назначении граничных условий на входах в каналы питания и управления диктуется требованиями устойчивого сходящегося итерационного процесса интегрирования задачи.

На входах в дренажные отверстия присвоено условие равенства статического давления, на выходе – атмосферному давлению. На выходе из каналов, где формируются выходные сигналы, граничное условие обеспечивает равенство статического давления потока на выходе из канала атмосферному давлению, подбирая потребный для этого расход. Стенкам каналов логического устройства присвоено условие непротекания. Данное граничное условие позволяет также мо-

a)

Рис. 1. Основные составные части (а) и геометрическая модель внутренних каналов (б) струйного двухвходового усилителя

Рис. 2. Расчетная сетка струйного двухвходового усилителя

Таблица 1. Результаты расчета параметров потока в каналах усилителя при увеличении давления в канале управления Х₁

Д авление
в каналах				Поле скоростей			Поле давлений
управления, Па
Px 1 =0, Px 2 =0.		Velocity V up Layer ■ 180			pressure 3 Down Layer ■ 19755
						12904
			90
			45			' '797 -J
			o 7			-7647
	Em sM]
Px 1 =590, Px 2 =0.		Up Це			Pressure PDrwnLai^r
			1»			11638
			и			1 3567
			46			| -4523
		■о »|M|				>af
							‘^^^L ° *^^^L °” *
Px 1 =3416, Px 2 =0.		' Doer Layer			Pressure P Drwn Lajmr
			142			13584
			96			1 6126
			IT			I -1333
		m	^1		pal
Px 1 =4814, Px 2 =0.		' Up Layer ■ 189			Pressire PD
			141
			94		■ 9169
			47
		m	0 ¥^1J

Таблица 2. Результаты расчета параметров потока в каналах усилителя при уменьшении давления в канале управления Х₁

Давление в каналах управления, Па Поле скоростей Поле давлений Px1=7792, Px2=0. (г Dcnm Layer ] 49               М RlM] Pressure Р Interface Ptw ■ 24323 iz668 В -8175           _ * -19008 Px1=2502, Px2=0. (г Layer Pressure р Up layer ■ 20588 [Р^75 Px1=1169, Px2=0. Dmrm Layer г \Л 1 44 Pressure              —. PDi;

При расчётах были приняты следующие параметры среды: газ - воздух, сжимаемый, вязкий, температура воздуха 25°С, динамическая вязкость 1,831 ⋅ 10^-5Па×с, начальная плотность 1,18 кг/м³. режим теплообмена – изотермический, атмосферное давление 101325 Па. Под термином давление далее подразумевается статическое давление, являющееся величиной превышения давления над атмосферным.

Некоторые результаты численного расчета параметров потока в каналах струйного двухвходового усилителя при увеличении и снижении давления в канале управления Х1 приведены в таблицах 1 и 2 соответственно.

Аналогичным образом были проведены расчеты по управляющему каналу Х2. На основании полученных результатов построены характеристики переключения двухвходового усилителя для каналов Х1 и Х2 (рис. 3).

в канале Х1 до 590 Па и в канале Х2 до 1152 Па. Внешний вид полученных характеристик струйного двухвходового усилителя качественно совпадает с теоретическими характеристиками. Это позволяет утверждать об адекватности разработанной математической модели и возможностях её применения для расчета параметров потока газа в каналах струйных элементов.

ВЫВОДЫ

Разработана математическая модель и методика численного расчёта параметров потока газа в малых каналах струйных элементов с использованием программных продуктов течения газа в каналах струйного двухвходового усилителя.

На основе математического моделирования методами вычислительной газодинамики получены картины течения газа внутри каналов устройства на различных режимах, включая поля скоростей и давлений.

a)

Рис. 3. График зависимости относительного расхода воздуха в канале У₂ от относительного давления в канале питания Х₁ (а) и Х₂ (б)

б)

Анализ результатов моделирования позволяет утверждать, что рассматриваемый струйный элемент способен функционировать согласно заданной схеме логических состояний при включении/отключении соответствующих управляющих сигналов. При отсутствии давления на управляющих сигналах струя питания на нижней плате усилителя отклонена влево, что позволяет формировать соответствующий управляющий сигнал на верхней плате усилителя для формирования выходного сигнала в канале У1. При повышении давления в управляющем канале Х1 до 4815 Па и в канале Х2 до 4384 Па происходит переключение питающей струи в нижней плате усилителя, что влечет за собой переключение выходного сигнала на верхней плате усилителя, создавая расход в канале У2. Обратное переключение двухвходового усилителя происходит при снижении давления

Определены рабочие характеристики струйного двухвходового усилителя, качественно подтверждающие логику работы устройства, что свидетельствует о высокой достоверности применяемой модели течения газа в каналах струйного устройства.