Методика формирования оптимального размещения элементов системы физической защиты (СФЗ) охраняемого объекта

В условиях возрастающих угроз (развития терроризма) и повышения возможностей современных информационных технологий задача совершенствования, оценки и оптимизации системы физической защиты (СФЗ) становится все более актуальной. Это связано в первую очередь с возрастающей сложностью СФЗ и увеличением числа альтернативных вариантов построения системы. В то же время важность решения задачи обеспечения безопасности объектов жизнедеятельности человека предъявляет жесткие требования к эффективности СФЗ и рентабельности проектных решений, что диктуется условиями рыночной экономики. Сложный и дорогостоящий процесс проектирования СФЗ предъявляет жесткие требования к проектным решениям, особенно принятым на ранних стадиях разработки проекта.

Функциональная модель построения СФЗ представляет собой последовательность взаимосвязанных этапов. Завершающим и важным этапом разработки СФЗ является синтез оптимального варианта размещения технических средств защиты (ТСЗ) на объекте.

Постановка задачи

При организации системы физической защиты объекта используется классический принцип последовательных рубежей, при нарушении ко- торых угрозы своевременно обнаруживаются и их распространению будут препятствовать надежные преграды. Оптимальное расположение зон безопасности и размещение на них ТСЗ (обнаружения и противодействия) составляют основу физической защиты любого объекта [1]. Разработка методики формирования оптимального варианта размещения технических средств защиты на объекте и является целью настоящих исследований.

Для решения этой задачи необходимо разработать автоматизированную модель формирования логико-вероятностных функций проникновения, на основе которых осуществляется оптимизация размещения элементов СФЗ. Вопросы оценки эффективности с использованием логико-вероятностных методов (ЛВМ) рассматривались в [4-5] с акцентом на большую трудоемкость ЛВМ, в качестве показателя эффективности СФЗ была введена вероятность нахождения системы в безопасном состоянии. В настоящей статье при проектировании СФЗ критерием оптимизации также является достижение заданной вероятности обнаружения угрозы и вероятности своевременного прибытия в точку пресечения группы реагирования при минимальной стоимости на проектирование, монтаж, и эксплуатацию элементов СФЗ.

Решение задачи

Рассмотрим модельный пример, представленный на рис. 1. Вся территория объекта имеет двойное ограждение, периметровую охрану и контрольно-пропускную систему. Каждая зона объекта характеризуется множеством параметров и имеет разный уровень важности. На объекте имеется секретное помещение (СП), подлежащее охране.

Концептуальная модель развития опасности проникновения угрозы представлена в виде разветвленного ориентированного мультиграфа (см. рис. 2). Вершины мультиграфа обозначены как рубежи достижения нарушителем определенного результата на пути к СП. Дуги мультиграфа – это варианты перемещений (связей) нарушителя между рубежами, представленные как логические переменные функций. Дуги будем обозначать Xi, где i – номер дуги в графе. Полученный граф будем называть моделью достижимости нарушителя своей цели. Всего будем определять n рубежей. Следовательно, граф будет иметь n вершин (событий). Инициирующему событию Yo присваивается значение «1». Наступление конечного события Yn означает факт проникновения нарушителя на объект, то есть нарушитель достиг своей цели (проведение диверсии и т.д.). Для данного графа вероятность нахождения Yn события в безопасном состоянии и будет показателем эффективности СФЗ.

На рис. 2 обозначено: X1 … Х10 – варианты преодоление КПП, первого и второго ограждения объекта; Х11 … Х18 – варианты перемещения через зоны между рубежами внутри объекта.

Необходимо определить все пути перемещений из начальной вершины Y0 в конечную вершину Y10. Все варианты пути из одной смежной вершины в другую будем обозначать как дизъюнкцию логических переменных, которыми являются веса каждой дуги, принятые за единицу в данной задаче. Например, перемещение из вершины Y0 в вершину Y1 будем обозначать X1 V X2 V X3. Пути из одной вершины в другую опреде-

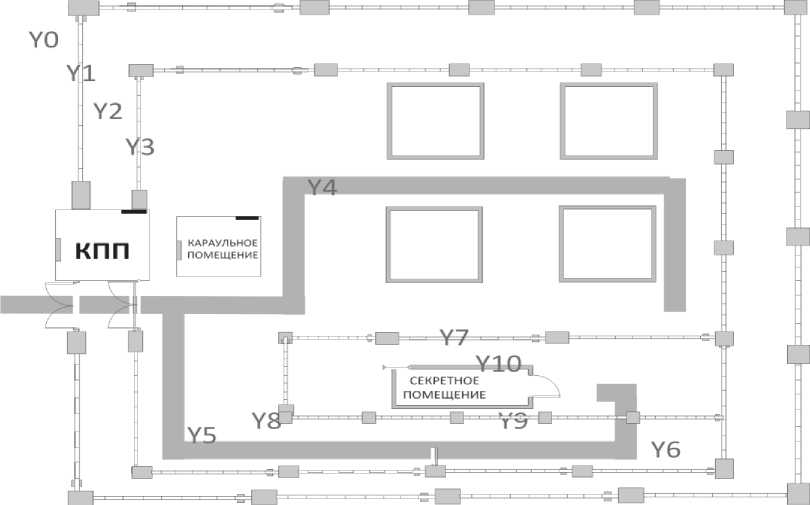
Рис. 1. План объекта

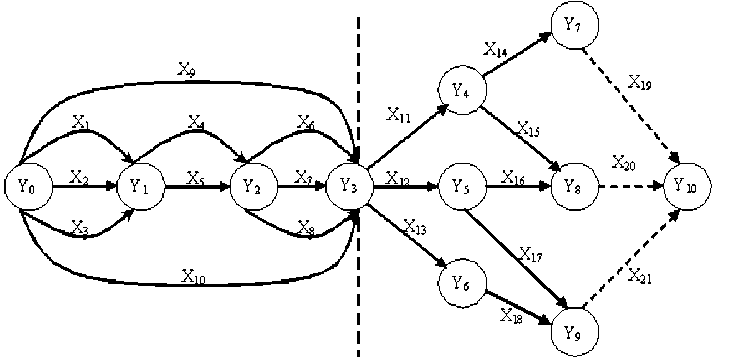
Рис. 2. Граф достижимости нарушителем своей цели

лялись с помощью операции композиции матриц смежности мультиграфа.

Реализовано программное средство, позволяющее находить все пути заданной длинны (если такие имеются) из первого рубежа в последний, представленные как функции алгебры логики (ФАЛ) в виде конъюнкции весов дуг, по которым проходит путь. Входные данные в программе представлены в виде матрицы смежности, в которой операцию конъюнкции двух переменных X1 X2 будем обозначать X1X2, а операцию дизъюнкции переменных X1 v X2 будем обозначать X1 + X2 (см. рис. 3).

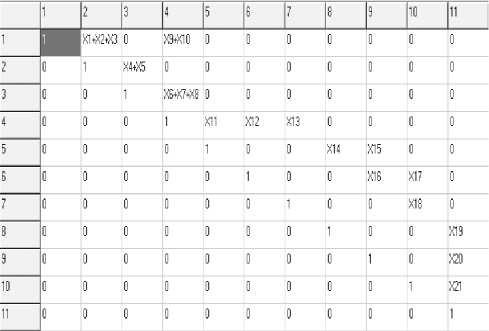
Рис. 3. Матрица смежности графа

Всего получили сто логических функций опасности, из которых десять длиной в четыре элемента, а девяносто длиной в шесть элементов. Полученные ФАЛ сведены в матрицу инцидентности (см. таблицу 1): строки в матрице – маршруты проникновения (функции), а столбцы элементы объекта (ребра), на которых будут формироваться ТСЗ СФЗ.

Элементы матрицы в строке связаны конъюн-ктивно, а в столбцах дизъюнктивно. Полученные логические функции развития опасности позволяют оценить вероятности проникновения каждого маршрута, то есть оценить эффективность СФЗ объекта. В вероятностном смысле эффективность СФЗ будет определяться вероятностью нереали-зации ни одной из ста функций проникновения.

Каждая функция проникновения предотвращается путем прерывания маршрута хотя бы в одной дуге. Необходимо исключить все сто маршрутов (функций) проникновения. Это задача о нахождении минимального сечения на графе, которая решается путем определения минимального покрытия на матрице инцидентности.

Задача о покрытии решалась методом ветвей и границ. Цель решения: минимальным количеством дуг перекрыть все возможные маршруты проникновения на объект. Результат покрытия – это минимальный набор дуг (препятствий) для исключения проникновения.

Таблица 1. Матрица инцидентности

Функции угроз

Дуги графа

X

сч X

х

X

их X

40 X

X

ОО X

04 X

о X

X

СЧ X

m X

хГ X

UX X

40 X

X

ОО X

04 X

о сч X

СЧ X

1

1

1

1

1

.              .              .

100

1

1

1

1

1

1

Дуга в графе может ассоциироваться с каким-то типом варианта защиты объекта, который будет характеризоваться вероятностью защиты и стоимостью. Так как задача о покрытии решается на максимум эффективности, то в качестве показателя выберем количество перекрываемых маршрутов с нулевой избыточностью. Тогда результатом будет множество покрытий, каждое из которых перекрывает все маршруты.

В результате решения задачи о покрытии для каждого столбца матрицы получили 22 покрытия, которые представлены в таблице 2. Каждое по- крытие позволяет контролировать все маршруты проникновения угроз в СП. То есть, на этих дугах и предполагается проектировать различные варианты построения элементов СФЗ.

Из 22 результирующих покрытий выбраны десять покрытий (1, 2, 3, 4, 5, 8, 9, 10, 12, 21). Двенадцать покрытий (6, 7, 12, 13, 14, 15, 16, 17, 18, 19, 20,22) исключены из рассмотрения, так как они попадают в зону непосредственной близости, в которой обнаружение нарушителя не позволяет силам охраны его перехватить.

Таблица 2. Таблица покрытий

Номер покрытия	Дуги покрытия
1	Х„ Х2, Х3, Х9, Хю
2	Х4, Х5, Х9, Х10
3	Х6, Х7, Х8, Х9, Хю
4	Хп, Х12, Х13
5	Х|2, Х|3, Х|4, Х|5
.    .   .	.     .     .
8	Хп, Х16, Х17, Х18
9	Х|2, Х|4, Х|5, Х|8
10	Х||, Х|6, Х|7, Хп
И	Х]4, Х15, Х16, Х21
12	Х|4, Х|5, Х|6, Х|7, Х|3
.    .   .	.     .     .
22	Хп, х15, х16, х17, х]8

Оптимизация размещения ТСЗ

Учитывая то, что вероятности обнаружения и вероятность перехвата угрозы обоснованны и заданы на предыдущих этапах проектирования СФЗ, будем решать задачу минимизации стоимости затрат на реализацию СФЗ при заданной вероятности противодействия угрозам [3].

Зададим требования к СФЗ: вероятность обнаружения угрозы на каждом маршруте не менее 0,92 – вероятности своевременного прибытия в точку пресечения группы реагирования на каждом маршруте не менее 0,5. В этой постановке необходимо на полученном множестве оценить стоимость и эффективность комбинаций покрытий. Логично считать, что стоимость покрытия зависит от протяженности покрытия, то есть стоимость С = KL, где L – длина покрытия; К – коэффициент пересчета. Каждое покрытие еще характеризуется расположением на местности, то есть его удалением от охраняемого объекта. Этот параметр вводится для оценки временной возможности противодействия и нейтрализации угрозы. Для этого выделяется критическая зона – минимальное расстояние от элемента охраны, после которой противодействие из-за недостатка времени невозможно. Все покрытия, которые попадают в эту зону, исключаются из процесса оптимизации.

Определив длину каждого покрытия, необходимо по строить возрастающий ряд. В первую очередь в оптимальное множество сечений включаются покрытия с минимальной протяженностью и необходимым удалением от охраняемого объекта. Оптимизация заключается в получении минимальной длины покрытий (стоимости) при обеспечении заданной вероятности обнаружения. Каждое дополнительное покрытие будет повышать вероятность обнаружения угрозы и вероятность распознать ситуацию поведения угрозы (конкретный маршрут движения) для принятия решения эффективной нейтрализации угрозы. Формирование множества покрытий заканчивается при достижении заданной вероятности обнаружения. Построение элементов обнаружения на данных покрытиях позволит получить СФЗ с заданной вероятностью обнаружения при минимальной стоимости.

Данная задача решается методом динамического программирования (ДП). Таким образом, при достижении заданной вероятности обнаружения угрозы выбирается вариант построения элементов СФЗ с наименьшей стоимостью.

Запишем номера покрытий по возрастанию их протяженности: 12 – 660 м, 9 – 670 м, 5 – 770 м, 8 – 780 м, 10 – 880 м, 21 – 890 м, 4 – 990 м , 3 – 2310 м, 2 – 2410 м, 1 – 2510 м. Множество покрытий делится на две группы, которые находятся внутри объекта (12, 9, 5, 8, 10, 21, 4) и за пределами (3, 2, 1). Как показывает практика, на внешние покрытия устанавливают датчики движения, это короткое покрытие 3. На внутренние покрытия устанавливают камеры наблюдения [6].

Для каждого покрытия определим удаление от СП и по этой величине определим вероятность перехвата нарушителя. Удаление СП от караула составляет 300 м. Удаление покрытий от СП: 12 – 280 м, 9 – 300 м, 8 – 320 м, 5 – 350 м, 10 – 450 м, 21 – 400 м, 4 – 460 м.

Для вычисления величины вероятности своевременного прибытия в точку перехвата Р(Т) используется модель, отражающая монотонный рост вероятности своевременного прибытия сил охраны по мере увеличения времени задержки нарушителей на физических барьерах (заборы, преграды, замки и т. п.) [6]:

Р<п = exp[l,7(^ -^j/crj/tl + exptlX, -t._f )M- (1)

Принимаем ограничения, что скорости движения угрозы и их среднеквадратичные отклонения соизмеримы со скоростями дви-

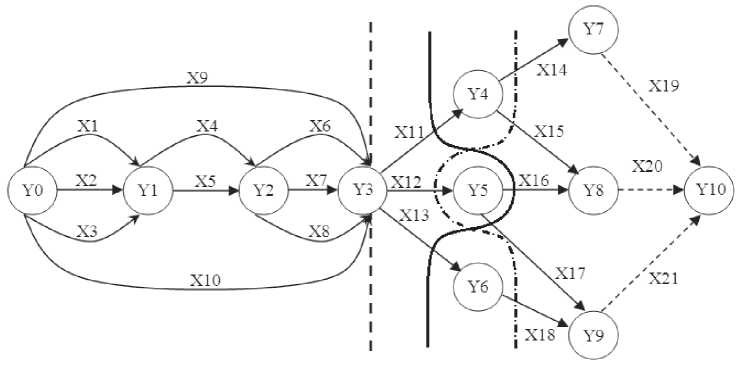
Рис. 4. Покрытия пресечения маршрутов проникновения (утолщенная штриховая линия – граница объекта; сплошная линия – 9 покрытие; штрих-пунктирная линия – 10 покрытие)

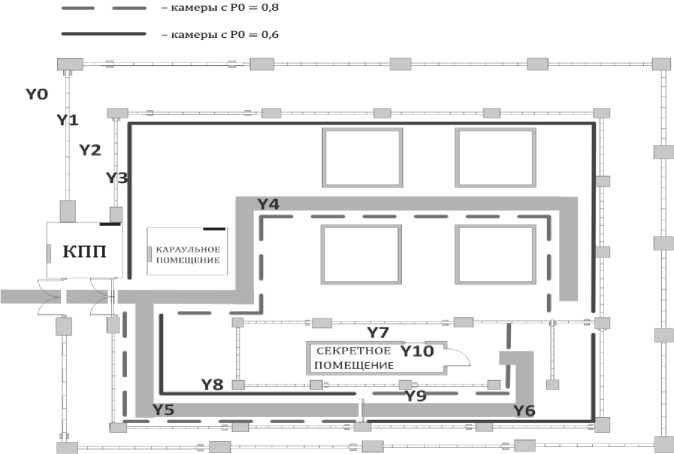
Рис. 5. Оптимальное расположение СТЗ (камер видеонаблюдения) на объекте

жения группы реагирования. Поэтому в формуле (1) перейдем от времени движения к расстояниям.

Покрытие 12 – не удовлетворяет по Р(Т). Для оставшихся покрытий 9, 5, 8, 10, 21, 4 проведем операцию дискретной разности множеств с целью исключения одинаковых ребер в покрытиях. Девятое покрытие объединяется с 5 в пользу 5, восьмое покрытие объединяется с 10 в пользу 8 как более короткое. Так как 21 и 4 покрытия пересекаются с 8 и 5 покрытиями, то необходимо их исключить в соответствии с постановкой задачи. Очевидно, что для обеспечения вероятности обнаружения 0,92 необходимо не более двукратного дублирования камер.

Таблица 3. Характеристики средств наблюдения

Тип средства	Стоимость, рублей	Вер-сть обнаружения	Угол обзора	Дальность, м
Камера CNB-WFL-21S	4800	0.60	70-90	60
Камера SCA-NALL	7000	0.80	70-90	70

На основе метода иерархий определены наиболее приемлемые технические средств обнаружения, характеристики которых представлены в таблице 3. Получаем два варианта покрытий: 5 – 770 м и 8 – 780 м или 9 – 670 м и 10 – 880 м с одинаковой длиной 1550 м, поэтому из двух вариантов решения задачи ДП можно выбрать наилучший.

Заключение

Оптимальным по выбранному критерию является вариант: на 9 покрытие устанавливаются камеры с вероятностью 0,8; на десятое – 0,6. Таким образом, каждый маршрут проникновения имеет заданный уровень вероятности обнаружения (не меньше и не больше, что очень важно [1]). Другое расположение камер на покрытиях приводит к увеличению стоимости, а также нарушению принципа проектирования – равнопрочности СФЗ.

На рис. 4 представлен граф с изображением девятого и десятого покрытий, на которых необходимо разместить ТСЗ объектов. На рис. 5 обозначено расположение камер видеонаблюдения.