Методика интеллектуального планирования операций с прерываниями работы автоматизированной мобильной системы сбора данных

Задачи с прерываниями являются практически значимым классом задач теории расписаний. Прерывания операций – естественная особенность многих процессов – от пакетной передачи данных по сети с вариацией времени и канала связи до необходимости охлаждать приборы во время работы. Если же речь идет о параллельно выполняемых операциях на разных устройствах, то можно провести аналогию с составлением вектора прерываний в многопроцессорной операционной системе. К этому классу относятся задачи управления работой химических реакторов в технологической схеме, оперативного управления испытаниями летательных аппаратов, анализа данных, поступающих в режиме реального времени со спутниковых систем, и др. Во всех этих ситуациях операция, выполняемая «устройствами» или «процессорами», должна быть прервана и возоб-

Методика интеллектуального планирования операций с прерываниями работы ...

Певнева Анна Геннадьевна кандидат технических наук, доцент, доцент кафедры математического и программного обеспечения, Военно-космическая академия имени А.Ф. Можайского, Санкт-Петербург. Сфера научных интересов: математическое моделирование объектов, процессов и систем, проектирование информационных систем. Автор более 30 опубликованных научных работ. SPIN-код: 2898-4704, AuthorID: 259511.

Заметим, что в теории расписаний в основном разработаны модели и задачи без прерываний. Объяснение, которое приводится в [1, с. 50], состоит в том, что в каждой конкретной задаче требуется проводить процедуру редукции континуального множества прерываний и множества допустимых точек прерывания каждого процесса к множествам конечной мощности, чтобы реализовать переборный алгоритм для оптимального расписания. Эта процедура сводится к анализу структуры оптимальных решений. Но для большинства задач теории расписаний такой анализ трудноосуществим, так что многопроцессорные задачи с прерываниями являются сегодня актуальными как с практической, так и с теоретической точки зрения [2]. Многие работы содержат описания реализации алгоритмов построения допустимых решений и исследование их свойств, например [3].

Целью данного исследования является обеспечение информационной полноты описания процесса сбора и обработки информации в режиме реального времени. В данной работе приводится описание частной методики составления допустимого расписания работы составляющих узлов (элементов) распределенной мобильной автоматизированной системы сбора данных (далее – МАССД). Такие системы призваны выполнять задачи получения данных в различных точках местности в процессе перемещения их по пунктам сбора данных (далее – ПСД), а длительность выполнения операций каждого узла зависит от внешних условий, например, погодных или сейсмических. Примером такой системы может служить гравиметрия, магнитометрия и сейсмометрия в точках профиля на мест- ности. Однако, применяя принцип аналогии, можно построить модель для процесса сбора данных любой распределенной системой, в том числе специфического назначения.

Во всех работах при выборе наиболее подходящего расписания ведущую роль играет эксперт – лицо, принимающее решение (далее – ЛПР). В качестве теоретического критерия оптимальности можно выбрать свойство выполнимости задачи, хотя в некоторых работах, например [4; 5], используется термин «живучесть». Согласно [6] живучесть автоматизированной системы – это «свойство, характеризуемое способностью выполнять установленный объем функций в условиях воздействий внешней среды и отказов компонентов системы в заданных пределах». Столь расплывчатое определение, на наш взгляд, не совсем подходит для строгой формальной математической модели.

Математическая модель задачи сбора данных элементами МАССД

Формализацию подхода к разработке математического аппарата выработки решения ЛПР по применению элементов МАССД в условиях возможного прерывания необходимо начать с описания исходных данных.

Пусть N 1 – количество элементов МАССД, выполняющих задачи по сбору данных в пунктах данного района, N 2 – количество задач, которые необходимо выполнить в течение цикла сбора данных на каждом пункте сбора данных (ПСД). Заметим, что в общем случае число задач может быть различным для каждого ПСД. Пусть также Т – общее время выполнения цикла сбора данных в этом районе. Кроме того, для каждого пункта сбора данных определяется длительность цикла сбора данных – T _p.

Район разбит на участки прямоугольной формы, в каждом участке не более одного ПСД. Дорожная сеть в районе применения элемента МАССД представляется графом

G = {{H1,H2,-,Hm},{V1^-Vp}} , где Hm,Vp – дороги и ПСД соответственно.

Каждое ребро этого графа как элемент дорожной сети характеризуется вектором проходимости PR для элементов данной МАССД. Этот вектор показывает, насколько эффективно мобильный элемент автоматизированной системы может двигаться по пути, обозначенному ребром Н _m . У этого вектора как минимум три компоненты: длина пути в данных единицах измерения L _m, средняя скорость v _mp движения по данной дороге в пункт V _p (эта величина может зависеть от рельефа), наличие объектов различной инфраструктуры Inf (например, населенные пункты или гидротехнические сооружения), которые уменьшают скорость передвижения.

Задаются временные характеристики модели:

t _n^нач – моменты выдвижения n -го элемента МАССД на задания по сбору данных;

t _pn– длительности выполнения операций каждым элементом МАССД на каждом ПСД; τ_n – интервалы непрерывной работы n -го элемента;

t _{1 n} , t _{2 n} – длительности прерываний как минимум двух типов для каждого элемента МАССД.

Прерывания первого типа включают в себя технологические и конструктивные особенности каждого элемента. Они характеризуются интервалом непрерывной работы элемента и длительностью прерывания. Прерывания 2-го типа обусловлены возможностью возникновения случайных условий, в которых необходимо прекратить выполнение операции или движение по дороге. Они характеризуются эмпирическим распределением вероятностей p _pn, которое оценивается наблюдаемой частотой возникновения таких условий, так что прерывания характеризуются некоторой весовой функцией

Методика интеллектуального планирования операций с прерываниями работы ...

t 1 n w pn {         .

t 2 n p pn

Могут также задаваться длительности прекращения операций сбора данных после сигнала о прерывании каждого типа для каждого элемента МАССД - Ai n ,.

Для подробного описания методики можно указать способы выхода элементов на ПСД: последовательный W 1 и параллельный W 2 и варианты ухода элементов с ПСД с целью повышения живучести: Ψ₁ – заблаговременный выход до сигнала о прерывании, Ψ₂ – сворачивание деятельности после сигнала о прерывании.

В модели могут учитываться возможности замены элементов МАССД при сигнале о прерывании в зависимости от типа прерывания – q ₁, q _2.

Формализация критерия выполнимости задачи делается на основе очевидного рассуждения: сбор данных на каждом пункте считается полностью выполненным, если в течение одного цикла выполнены все N 2 задач. Задача считается выполненной, если элементы МАССД отработали все время t _pn. Если же это в реальных условиях невозможно, то необходимо построить такой маршрут движения элементов МАССД по району сбора данных, при котором фактическое время T _p^факт = ∑( T _pn^факт) исполнения задач на каждом ПСД с учетом перемещения элементов между пунктами и прерываний всех типов минимально отличается от установленного времени T _p.

Таким образом, требуется построить множество допустимых расписаний маршрутов движения всех элементов МАССД в районе сбора данных при наличии прерываний:

^ = {k (tЩТ), k =1-K}, k ={(V,Vk)}, где k – число маршрутов; i, j – номера ПСД в маршруте, i, j = 1…Р;

TЛ - tpn + wpn + Z((Lk /vnk) + wkn).

k

В этом множестве необходимо выбрать такой маршрут, для которого

Tp— (Tрфакт) ^ min.(3)

При этом суммарное фактическое время выполнения задач не превосходит заранее заданную величину Т – общее время выполнения цикла сбора данных, то есть задано огра- ничение

∑_р( T _p^факт) <  T .

Методика расчета расписания движения элементов мобильной автоматизированной системы в условиях прерываний

Представленная ниже методика является ограничением полного перебора маршрутов движения элементов МАССД по всем имеющимся ПСД с учетом возможных прерываний.

• 1.    Район выполнения задач разбивается на прямоугольные участки, содержащие не более одного ПСД.

• 2.    Для каждого p -го участка вычисляется время пребывания в нем n -го элемента T _pn, которое складывается из времени выполнения задачи для ПСД, который расположен на этом участке, и времени движения к нему из текущей точки. При этом необходимо учитывать возможность прерывания как выполнения операций по сбору данных, так и прерывания во время движения. Расчет производится по формуле (2). Суммирование в формуле (2) производится по тем участкам, через которые должен проследовать элемент МАССД.

• 3.    После расчета таблицы элементы МАССД распределяются по задачам. Для этого из таблицы из разных строк и столбцов выбираются N элементов и сортируются по возрастанию. Порядок первых индексов – это порядок посещения ПСД элементами МАССД.

• 4.    Для элемента, который закончил выполнение задачи раньше всех, пересчитываем столбец таблицы, при этом исключив из таблицы строку с выполненным заданием.

• 5.    Переход к шагу 3.

Результаты заносятся в таблицу.

Таблица

Расчетное время выполнения задач на каждом шаге

№ ПСД	№ элемента
	1	2	…	N
1	T 11	T 12		т 1N
2	T 21	T 22		т 2N
P	T P1	T P2		т PN

Для визуализации результатов необходимо разработать специализированный скрипт для скачивания фрагмента карты. После этого вся дальнейшая работа происходит без подключения к интернету. Формирование вершин дорожного графа производится только там, где осуществляется движение в пределах фрагмента карты и доступных дорог от пункта начала движения.

Входные данные, которые использовались для анализа карты: формат карты Open Street Map , формат данных о дорогах GeoJSON . Файл содержит список дорог. Дороги содержат идентификатор, приоритет (трасса, городская дорога и др.), тип покрытия, координаты пути, факт наличия мостов (см. Рисунок). Вероятности возникновения нештатных прерываний моделировались с использованием встроенных генераторов равномерного распределения.

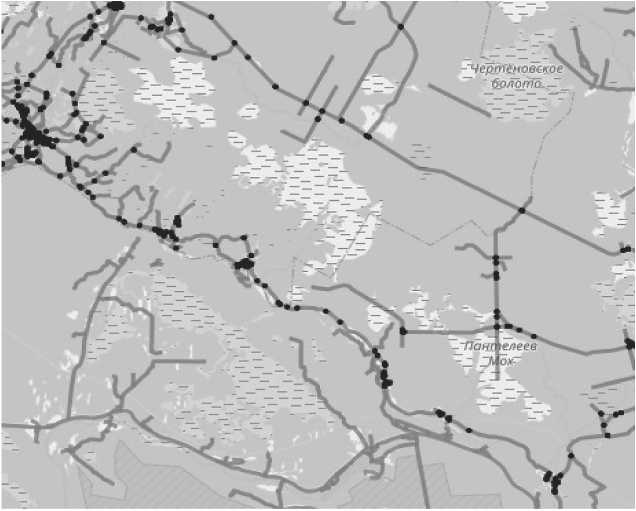
Рисунок. Граф дорожной сети: линии – доступные дороги, точки – вершины графа – координаты сбора данных

Методика интеллектуального планирования операций с прерываниями работы ...

Заключение

Представленная методика показала себя работоспособной. Затраченное время расчетов маршрутов для двух, трех и четырех мобильных элементов не превышало 10 мс. Составленные маршруты отражаются в виде таблицы, но их визуализация без использования специализированных функций API ГИС представляет значительные трудности и является самостоятельной инженерной задачей.

Рассмотренная в работе задача составления расписания маршрутов движения на местности при необходимости прерывания операций является перспективной с точки зрения уточнения математической модели: в данных расчетах не учитываются возможные переменные длительности нештатных и случайных прерываний и не рассмотрен вопрос влияния на результаты расчетов распределений вероятностей этих прерываний. В целом возникновение таких прерываний можно рассматривать как самостоятельный случайный процесс.