Методика компьютерного исследования жесткости спице-стержневых фиксирующих устройств

В настоящее время приобретает особую актуальность проблема разработки в сжатые сроки конструкции аппарата внешней фиксации, удовлетворяющего требованиям прочности и надежности. Компоновка спице-стержневых фиксирующих устройств проводится в два этапа: первый этап – подготовительный, второй – установка и монтаж. Подготовительный этап предполагает определение геометрии конструкции и расчет жесткости фиксирующего устройства, которая определяется как способность элементов конструкции сопротивляться перемещениям. Отказ от исследования жесткости фиксирующего устройства увеличивает риск возникновения осложнений, может сказаться на результатах лечения повреждений костей. Травматологами разработана методика исследования жесткости спице-стержневых устройств [2], предусматривающая сравнение показателей жесткости разрабатываемой конструкции с показателями жесткости эталонных модулей. В качестве эталонных модулей используются конструкционные элементы аппарата Илизарова, репозиционные способности и жесткость фиксации костных фрагментов которого за десятилетия использования подтверждали и подтверждают его эффективность. Показатели жесткости в соответствии с методикой определяются путем проведения стендовых испытаний, которые обладают рядом недостатков: наличие материальнотехнического обеспечения и обученного персонала для проведения стендовых испытаний; предварительное изготовление аппарата внешней фиксации.

В настоящей работе предложена методика компьютерного исследования жесткости спице-стержневых фиксирующих устройств, которая позволит избавиться от материально-технической стороны стендовых испытаний и в достаточно короткий промежуток времени получить ответ о возможности использования фиксирующего устройства для конкретного клинического случая.

Методика исследования

Жесткость фиксирующего устройства характеризуется коэффициентом жесткости, который определяется из отношения внешних нагрузок к линейным и угловым перемещениям. Чем больше коэффициент жесткости, тем больше жесткость. Измеряется коэффициент жесткости в Н / мм – для линейных перемещений (линейная характеристика жесткости), Н·мм / град – для угловых перемещений (угловая характеристика жесткости).

Возможность использования устройства определяется индексом Илизарова ( Ил ) [2]. Показатели жесткости исследуемого модуля сравниваются с показателями жесткости эталонных модулей при условии приложения к устройству стандартных смещающих усилий:

к

Ил = Кэт , (1) иссл где Кэт – коэффициент жесткости для эталонной модели, Киссл – коэффициент жесткости для исследуемой модели. Если Ил ≤ 1, то исследуемый модуль превышает или равен по жесткости эталону; если Ил > 1, то исследуемый модуль по жесткости уступает эталону.

Рассмотрим методику исследования жесткости фиксирующего устройства. Первый этап – определение геометрических параметров конструкции, точное и однозначное описание которой выполняется на основе метода унифицированного обозначения чрескостного остеосинтеза [6]. Функциональной единицей в построении аппаратов внешней фиксации является внешняя опора (кольца, полукольца, секторы) с закрепленными в ней одним или несколькими чрескостными элементами. Эта функциональная единица обозначена как «модуль первого порядка» (M l ) и представлена на рис. 1. Геометрические параметры модулей первого, второго и третьего порядков представлены на примерах эталонных моделей.

В качестве эталонной модели для модулей первого порядка (М 1э ) принята модель на основе кольцевой опоры из комплекта аппарата Илизарова с внутренним диаметром 160 мм. Длинную ось имитатора кости располагают в центре кольцевой опоры. Диаметр спиц – 2 мм, угол перекреста спиц – 60°. Длина имитатора кости – 170 мм. Спицы проходят на расстоянии 25 мм от проксимального конца имитатора кости – принятая локализация уровня I.

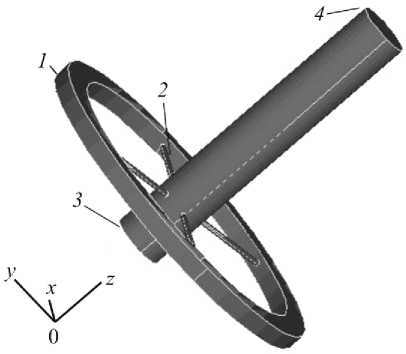
Рис. 1. Модуль первого порядка (М_{1 э} ): 1 – кольцевая опора, 2 – спицевой элемент, 3 – проксимальный конец имитатора кости, 4 – дистальный конец имитатора кости

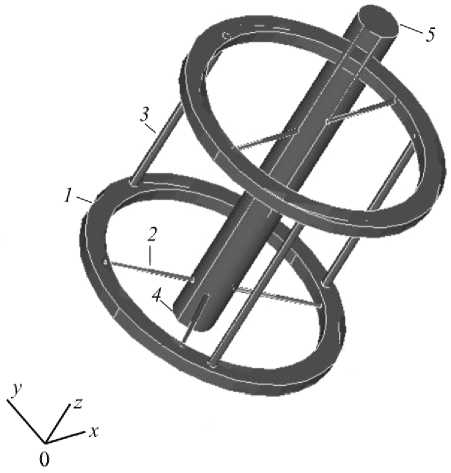
Рис. 2. Эталонный модуль второго порядка (М_{2 э} ): 1 – кольцевая опора, 2 – спицевой элемент, 3 – штанга, 4 – проксимальный конец имитатора кости, 5 – дистальный конец имитатора кости

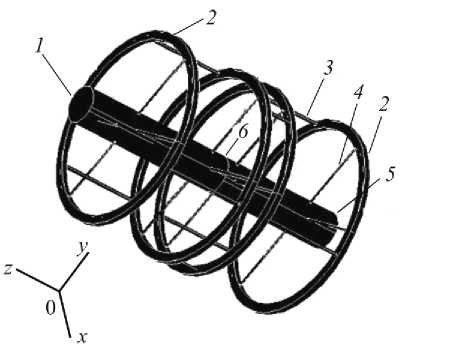
Рис. 3. Эталонный модуль третьего порядка (М_{3 э} ): 1 – дистальный фрагмент имитатора кости, 2 – кольцевая опора, 3 – штанга, 4 – чрескостный элемент (спица), 5 – проксимальный фрагмент имитатора кости, 6 – диастаз

За эталонный модуль второго порядка (М 2э ) принята модель на основе двух кольцевых опор, расположенных на расстоянии 150 мм и соединенных тремя штангами (рис. 2). Длина имитатора кости – 280 мм. Спицы проксимальной опоры проводят, отступая на 25 мм от проксимального конца имитатора кости – принятая локализация уровня I. Расстояние между уровнями принято равным 50 мм. Спицу с упорной площадкой второй опоры проводят на уровне IV, отступая на 150 мм от уровня I.

Эталонный модуль третьего порядка (М3э) – полная компоновка чрескостного аппарата, состоящего из двух эталонных модулей второго порядка, соединенных тремя штангами диаметром 6 мм и длиной 100 мм (рис. 3). Соединенные с костью и друг с другом опоры образуют раму аппарата. Рама фиксируется с костью с помощью чрескостных спиц, которые будем рассматривать как тонкие стержни с диаметром 2 мм и длиной, не превышающей внутренний диаметр опоры. Длина имитатора кости – 500 мм. Спицы проксимальной опоры проводят, отступая на 50 мм от торца проксимального фрагмента имитатора кости – принятая локализация уровня I. Расстояние между уровнями принято равным 50 мм. Между костными фрагментами для возможности исследования реакции модели на смещающие нагрузки создают диастаз 2 мм.

При расчете основных характеристик жесткости фиксирующего устройства используем метод конечных элементов. Поэтому следующий этап методики – создание конечно-элементной модели фиксирующего устройства, для построения которой используем пространственный стержень, имеющий 12 степеней свободы (3 перемещения и 3 угла поворота в каждом узле) (рис. 4).

Одним из главных вопросов при использовании метода конечных элементов

является построение матрицы жесткости. Для выбранного конечного элемента она имеет вид [1] Г k 0 0 0 0 0 k1 0 0 0 0 0 " 0 k11 0 0 k12 0 0 k13 0 0 k14 0 0 0 k11 0 0 k12 0 0 k13 0 0 k14 0 0 0 k2 0 0 0 0 0 —к 2 0 0 0 k12 0 0 к 22 0 0 к 23 0 0 k24 0 r= 0 к1 0 0 k12 0 0 0 0 0 к 22 0 0 k1 0 0 к 23 0 0 0 0 0 k24 0 ,             (2) 0 k13 0 0 к 23 0 0 к 33 0 0 k34 0 0 0 k13 0 0 к 23 0 0 к 33 0 0 k34 0 0 0 —к 0 0 0 0 0 k2 0 0 0 k14 0 0 k24 0 0 k34 0 0 k44 0 L 0 0 k14 0 0 k24 0 0 k34 0 0 к44 J EF где к1 =    , к2 = GJp ,    k11 12 EJ k12 6EJ к 22 = 4EJ 2 EJ l l3 , l2 , l , 24 l ’ к zz — к   к zz к tv 13      Лц, Л14    л12, к = 23 —к 12, k34 zz — к tv 12, Е модуль упругости, G – модуль сдвига, J – момент инерции, Jp – изгибающий момент, F – площадь поперечного сечения, l – длина стержневого элемента.

Известно, что процессы деформирования натянутой спицы носят нелинейный характер, поэтому для решения задачи целесообразно использовать конечноэлементную теорию нелинейной деформации при линейных свойствах материала. Процесс решения нелинейной задачи очень сложный и трудоемкий. Задача упростится, если заменить нелинейную теорию линейной, например, усилив спицевой элемент за счет увеличения его радиуса. То есть спицу будем рассматривать как тонкий стержень и для его моделирования конечными элементами применим пространственный стержень (см. рис. 4). При нагрузке менее 70 Н, а при исследовании жесткости фиксирующего устройства нагрузка не превышает эту величину, прогибы, рассчитанные по нелинейной теории для спицы диаметром 2 мм и рассчитанные по линейной теории для спицы диаметром 2,8 мм, очень близки. Поэтому при исследовании жесткости фиксирующего устройства принимаем, что спица имеет диаметр 2,8 мм и для расчета ее деформаций используем линейную теорию метода конечных элементов.

Решение задачи методом конечных элементов требует задания граничных условий. Для модуля первого порядка жестко крепится внешняя опора, для модуля второго порядка – внешняя опора, расположенная вблизи проксимального конца имитатора кости, для модуля третьего порядка – проксимальный конец имитатора кости.

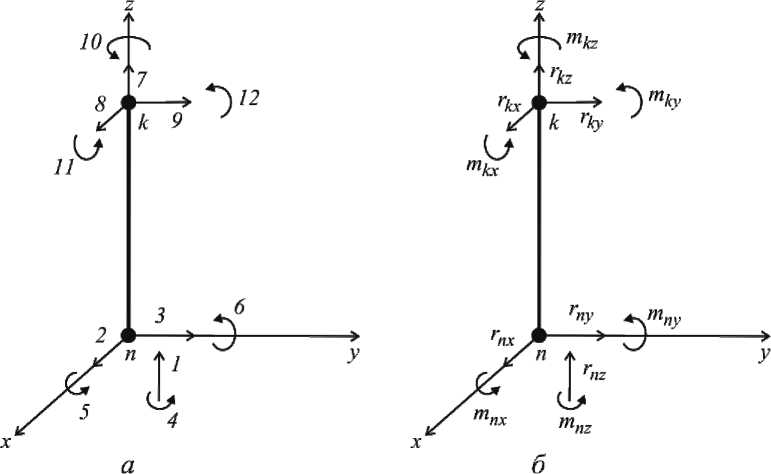
Рис. 4. Пространственный стержневой элемент с двенадцатью степенями свободы: a -обобщённые координаты, б – обобщенные силы, соответствующие обобщенным перемещениям

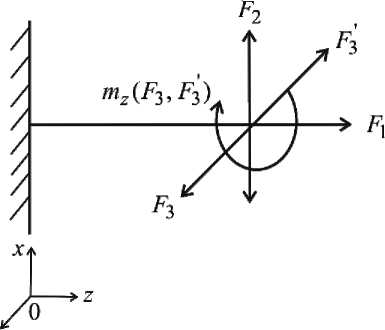
Рис. 5. Стандартные смещающие нагрузки

Следующий этап методики – определение коэффициентов жесткости модели. При исследовании жесткости остеосинтеза целесообразно исследовать реакцию моделей конструктивных модулей на стандартные смещающие нагрузки: осевая сила F 1 , поперечная F 2 , ротационная сила - пара сил ( F 3 , F ₃ ) c моментом m_z (рис. 5).

Задача состоит в определении так называемой предельной нагрузки, при которой смещение нагружаемого фрагмента имитатора кости в случае исследования модулей первого и второго порядка, и на стыке костных фрагментов в случае модуля третьего порядка достигает 1 мм или 1 ° .

Продольная нагрузка F 1 = 50 Н прикладывается к свободному дистальному концу имитатора кости, определяется максимальное перемещение имитатора кости u_z по оси z . Коэффициент продольной жесткости K 1 рассчитывается по формуле

К - F

^K 1 = 1 uz| •

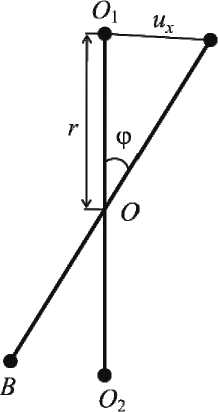
Рис. 6. Схема расчета угла поворота имитатора кости при поперечной нагрузке. AB – имитатор кости, O ₁ O ₂ – ось имитатора, φ – искомый угол, u_x – смещение дистального конца, r – расстояние от дистального конца имитатора кости до места проведения чрескостного элемента (точка O )

Поперечная нагрузка F 2 = 10 Н прикладывается в направлении сначала оси x (фронтальная плоскость), затем оси y (сагиттальная плоскость). Коэффициент поперечной жесткости есть сила, которая обеспечивает поворот имитатора кости относительно его оси на угол величиной 1º. Коэффициент поперечной жесткости K ₂ во фронтальной плоскости рассчитываем по формуле

F г 2 r

K 2         ,

ф где F2 r – момент силы F2, r – расстояние от дистального конца имитатора кости до места проведения чрескостных элементов, φ – угол поворота имитатора кости относительно оси z (рис. 6). При малых значениях ф имеет место формула ф = tg ф и u

tg ф= -, r где ux – величина смещения дистального конца имитатора кости.

При исследовании ротационной жесткости к дистальному концу имитатора кости прикладывается крутящий момент, направленный против часовой стрелки и равный 10 Н·мм . Величина момента, при которой имитатор кости повернется вокруг своей оси z на 1º, представляет собой коэффициент ротационной жесткости K ₃ и вычисляется по формуле

K = m ( ^F 3 ,^{F )}

3 Ф

,

где m_z ( F ₃, F ₃^') – момент пары сил, относительно оси z , φ – угол закручивания.

Используя коэффициенты жесткости исследуемой модели и эталонной модели по формуле (1), находим индекс Илизарова, на основании которого можно сделать вывод о возможности использования устройства в травматологии.

Численное моделирование

Расчеты выполнялись в среде пакета Matlab 6. Для определения коэффициентов жесткости модулей приняты параметры, соответствующие стали (именно этот материал используется для изготовления фиксирующих устройств): Е = 22,30∙10¹⁰ Па – модуль упругости (модуль Юнга), коэффициент Пуассона µ = 0,3, модуль сдвига G = 7,80∙10¹⁰ Па [3]. В качестве имитатора кости в исследованиях используется стержень диаметром 30 мм с параметрами костной ткани: Е = 18,35∙10⁹ Па – модуль упругости, коэффициент Пуассона µ = 0,307, модуль сдвига G = 4,91∙10⁹ Па [4]. В данных исследованиях в качестве имитатора можно использовать образцы из дерева, пластика, металла, так как при нагружении описанных моделей деформации имитаторов кости – величины малые по сравнению с деформациями чрескостных элементов аппаратов внешней фиксации.

Для исследования жесткости фиксирующих устройств необходимы значения коэффициентов жесткости эталонных модулей. В табл. 1 приводятся эти значения, полученные в ходе стендовых испытаний [2] и путем математического моделирования [5]. Сравнение результатов позволяет отказаться от натурных экспериментов при исследовании жесткости фиксирующих устройств.

Таблица 1

Показатели прочности для эталонных модулей, полученные в ходе стендовых испытаний и математического моделирования (мат. мод.)

Коэффициент	Ротационная жесткость, Н∙мм / град	Поперечная жесткость, Н∙мм / град		Продольная жесткость, Н / мм
		Сагиттальная плоскость	Фронтальная плоскость	Дистракция	Компрессия
К 1э (стендовые испытания)	11,0	3,0	7,0	63,0	63,0
К 1э ( мат. мод. ) Погрешность, %	10,80 1,9	3,10 3,7	7,25 3,5	62,50 0,7	62,50 0,7
К 2э (стендовые испытания)	16,0	8,9	15,6	54,0	54,0
К 2 э ( мат. мод. ) Погрешность, %	15,60 2,5	9,15 2,8	15,25 2,2	53,70 0,5	53,70 0,5
К 3э (стендовые испытания)	15,5	11,0	24,0	53,0	53,0
К 3 э ( мат. мод. ) Погрешность, %	15,1 2,6	11,3 2,7	23,2 3,3	54,0 1,9	54,0 1,9

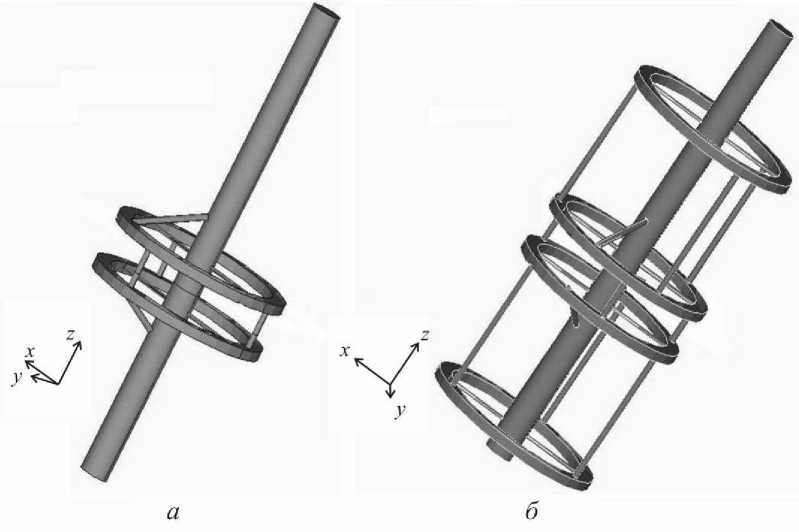
Рис. 7. Аппараты внешней фиксации

Таблица 2

Показатели прочности для фиксирующих устройств

№ п / п	Продольная жесткость, Н / мм				Поперечная жесткость, Н∙мм / град				Ротационная жесткость, Н∙мм / град
	Дистракция	Ил	Ком-прес-сия	Ил	Сагит-таль-ная плоскость	Ил	Фрон-таль-ная плоскость	Ил	Коэф-фици-ент жесткости	Ил
1	29,800	1,420	38,000	1,420	3,400	3,240	4,250	5,700	9,700	1,600
2	56,800	0,950	56,800	0,950	35,100	0,320	38,000	0,610	39,200	0,385

Рассмотрим два фиксирующих устройства, вид которых представлен на рис. 7. Для их обозначения используется метод унифицированного обозначения чрескостного остеосинтеза [6], который обеспечивает максимальный объем объективной детализированной информации: тип и пространственная ориентация чрескостных элементов, порядок и направление их проведения, геометрия и размеры внешних опор, состояние между опорами.

В табл. 2 приведены показатели прочности, рассчитанные для исследуемых фиксирующих устройств (см. рис. 7). Анализируя полученные результаты, отмечаем, что индекс Илизарова для всех показателей жесткости первого устройства (рис. 7, а ) превышает единицу, это означает, что исследуемая модель не превосходит эталонную по жесткости и не может быть использована в травматологии. Для второй модели (рис. 7, б ) индексы Илизарова не превышают единицы, следовательно, устройство может быть использовано при лечении переломов костей.

Заключение

Предложенная методика компьютерного исследования жесткости фиксирующего устройства обладает рядом преимуществ по сравнению с методикой, основанной на стендовых испытаниях: не требуется изготовления конструкции фиксирующего устройства; значительно сокращается время расчета показателей жесткости; имеется возможность создания пополняемой базы данных о моделях фиксирующих устройств и их показателях жесткости. Все это позволит ускорить подбор необходимой модели аппарата внешней фиксации.