Методика моделирования и расчета свойств неравновесных фаз молекулярных систем

Метод молекулярной динамики (МД) является уникальным инструментом моделирования термодинамических систем, позволяющим прослеживать фазовые траектории вещества. В настоящее время существует ряд программных решений основанных на МД, позволяющих моделировать молекулярные системы в равновесных состояниях. Однако, известные программные продукты (CHARMM, LAMMPS, HOOMD, GROMACS, NAMD) более направлены на моделирование состояний с заданными термодинамическими параметрами (ансамблей) и малопригодны для имитации термодинамических процессов протекающих с большой скоростью (быстрое охлаждение, быстрое прессование), поэтому неравновесное моделирование с помощью вышеуказанных программ сводится к инициализации систем в одних только критических областях и точках фазовых переходов. Наибольший же интерес представляет эволюция молекулярной системы в широком температурном интервале в процессе достаточно быстрого охлаждения. Нами предложена методика моделирования процессов быстрого изохорического и изобарического охлаждения молекуляр- ной системы, а также приемы расчета физических свойств материалов по результатам компьютерного эксперимента.

1. Классический метод молекулярной динамики

Методика МД заключается в решении уравнений движения для системы многих частиц. Так, силу, действующую на i-ю частицу, можно представить в форме суммы векторов d 2 r( t)    "-* dФ ( r)

m--= -> ---— dt2 j dr где Ф(г) - потенциал взаимодействия частиц системы, m - масса частицы, r - радиус вектор частицы.

Любой алгоритм, реализующий МД, сводится к наиболее оптимальному по производительности и точности численному интегрированию уравнения (1).Широкое применение имеет алгоритм Верле в скоростной форме, согласно которому координаты и скорости частиц на каждой итерации вычисляются в следующей последовательности:

, At2 r (t + at) = r (t)+vi (t) at+a i (t)     , (2) r( t+A) == ri( t)+1 а( t)A t, (3) 1 ^-i dO (rj) a , (t + A t) =    Z   Jr  , m j   drr (4) / A t_ _ , . x A t ri (t + A t) = ri (t + —) + a, (t + A t) — , (5) где ri, vi, ai - радиус-вектор положения, скорость и ускорение i-й частицы соответственно.

В отсутствие внешних сил система частиц должна прийти к термодинамическому равновесию с заданными температурой, плотностью и давлением. Проведение эксперимента, моделирующего термодинамические процессы, предполагает модернизацию алгоритма путем введения процедур корректировки скоростей (процесс изменения температуры системы) или размеров ячейки моделирования (процесс изменения плотности системы).

ячейки моделирования и расстояния между частицами для поддержания постоянного давления системы. На практике применяются два основных метода поддержания давления: баростат Андерсена [1] и баростат Бе-рендсена [2]. Метод Андерсена коренным образом меняет алгоритм Верле путем введения обобщенных координат связанных с размерами системы и скоростью изменения этих размеров, этот алгоритм довольно сложно реализуем, а жесткость баростата не позволяет моделировать процессы быстрого изменения температуры. В работе баростата Берендсена необходимо иметь известное значение изотермической сжимаемости для каждой точки фазовой траектории, что для моделирования неравновесных процессов невозможно.

Рапапорт [3] описывает организацию ансамбля с постоянным числом частиц, давлением и температурой. Здесь используется баростат, корректирующий положения частиц и размеры системы на коэффициент д , выведенный из лагранжиана ( NPT) -ансамбля:

„ = 1 ₊_____ P^(V )^- P _____,                          (6)

3 P (V) -V Фjrj|3V i < j где P - заданное давление, P(V) - давление, рассчитанное на данной итерации моделирования. Такой коэффициент пригоден для небольших флуктуаций давления и практически не поддерживает постоянным давление в процессе быстрого охлаждения. Однако, мы применили этот метод в циклической процедуре (рис. 1), позволяющей поддерживать давление с точностью 1% даже в случаях с резким перепадом температуры.

Вход в процедуру

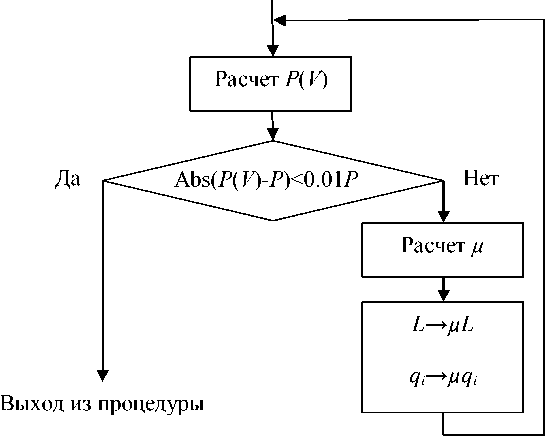
Рис. 1. Процедура баростатирования

Моделирование изобарного охлаждения дает возможность численного определения таких характеристик как изобарная теплоемкость С p и изотермическая сжимаемость β T .

Так, получив в результате компьютерного эксперимента температурную зависимость энтальпии H, можно вычислить изобарическую тепло- емкость:

Cp = [—1 .                           (7)

p I dT ) _P

Для определения сжимаемости необходимо получение двух изобар с близкими значениями давления P1 и P2. По разностям плотностей на фа- зовых кривых изотермическая сжимаемость определяется следующим выражением:

в т = — ^PP 1 <  p >  P 1

—

—

pP 1

^, P 2

где ρ P1 и ρ P2 – плотности систем под давлением P 1 и P 2 при одинаковых температурах.

• 3.    Апробация

На основе описанной методики разработана программа моделирования молекулярных систем MDDX11[4]. С помощью этой программы нами проведен ряд экспериментов, моделирующих процессы равновесного и неравновесного охлаждения системы частиц аргона.

На рис. 2 представлена температурная зависимость теплоемкости C p аргона полученная по результатам моделирования равновесного охлаждения аргона. Для сравнения здесь же представлены литературные данные [5].

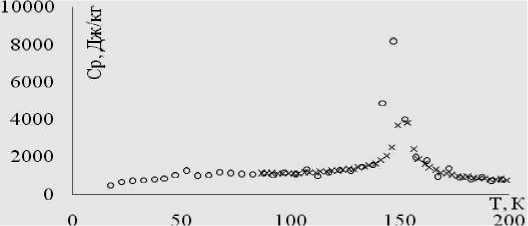
Рис. 2. Изобарическая теплоемкость аргона при давлении 5 МПа: o – результаты нашего компьютерного эксперимента, х – литературные данные [5].

Как видно, результаты хорошо согласуются с литературными данными, в областях фазовых переходов при температурах ~55 и ~155 К прослеживаются характерные изменения в зависимости C p ( T ).

На рис. 3 и 4 представлены результаты расчета сжимаемости по данным моделирования равновесного и неравновесного охлаждения соответственно.

0.5

0.4

0.3

0.2

0.1

о

10        60        110       160       210

Рис. 3. Изотермическая сжимаемость аргона при давлении 4 МПа по данным компьютерных экспериментов, моделирующих охлаждение аргона со скоростью 109 К/с.

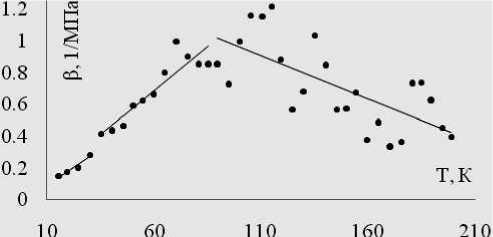
Рис. 4. Изотермическая сжимаемость аргона при давлении 4 МПа по данным компьютерных экспериментов, моделирующих охлаждение аргона со скоростью 1012К/с.

На графике температурной зависимости сжимаемости (рис. 3), полученной по данным эксперимента с равновесным медленным охлаждением, можно разделить газовую, жидкую и кристаллическую фазы.

Для неравновесного процесса охлаждения со скоростью 1012 К/с температурная зависимость сжимаемости (рис. 4) претерпевает резкое изменение в окрестностях точки ~90 К, возможно, это характеризует переход неравновесный газ (перенасыщенный пар) – неравновесная жидкость (смесь газа с кластерами жидкости). Также можно отметить переход в окрестностях ~30 К, вероятно соответствующий переходу нестабильной жидкости в аморфную фазу.

Заключение

Предложена методика моделирования равновесных и неравновесных молекулярных систем, позволяющая рассчитывать изобарическую сжимаемость и изотермическую теплоемкость. Результаты апробации хорошо согласуются с эмпирическими данными и наглядно демонстрируют фазовые закономерности вещества при равновесном и неравновесном охлаждении.