Методика моделирования лесной почвы при взаимодействии с рабочими органами лесохозяйственных машин

В настоящее время моделирование является важным этапом любого научного исследования или прикладной инженерной разработки, учитывая тот факт, что современная техника представляет собой крайне сложные технические объекты. Для создания лесных машин с высокими характеристиками эффективности и качества работы целесообразно использовать математическое моделирование. В частности, для теоретического исследования функционирования лесохозяйственных почвообрабатывающих машин разрабатывается математическая модель, описывающая взаимодействие рабочих органов орудий с почвой при их движении, а также перемещение почвенных частиц в пространстве.

Лесная почва характеризуется большим количеством физико-механических параметров, таких как твёрдость, влажность или плотность, а также типологическими особенностями в виде рельефа поверхности, насыщенности корневыми системами древесных и кустарниковых пород и т. д. [1]. Для моделирования такой структурно сложной среды целесообразно использовать метод конечных элементов, когда почва представляется большим количеством элементов шарообразной формы, которые могут взаимодействовать между собой, а также с рабочими органами лесной машины [2—9]. Взаимодействие рабочих органов с почвой представляет собой задачу нахождения расстояния г в от поверхности рабочего органа до сферической поверхности некоторого элемента почвы. Силу, действующую со стороны рабочего органа на почвенный элемент, можно определить по формуле

F = c • г_в • n - kv ,                                      (1)

где n и v — векторы скорости взаимодействия рабочей поверхности и элемента почвы; c и k — коэффициенты жёсткости и вязкости взаимодействия.

Трудоёмким этапом при моделировании является составление алгоритма расчёта сил, действующих со стороны рабочего органа на элементы почвы и вызывающих её деформацию и деление на отдельные частицы. Необходимо производить расчёт суммарной силы сопротивления со стороны почвенных частиц на рабочие поверхности почвообрабатывающих машин при их работе. Состояние каждого элемента i можно описать шестью переменными:

• — координатами его центра (xi, y,, zi);

3.    Результаты

— составляющими его скорости ( v_xi , v_yi , v _zi ).

Взаимодействие почвенных частиц друг с другом носит вязкоупругий характер, поэтому в модели учитывается упругость и вязкость почвы при воздействии на неё рабочих органов. В модели целесообразно изначально предположить, что все элементы почвы связаны между собой. Разделение двух элементов, в частности, при контакте с рабочими поверхностями, приводит к их отрыву друг от друга [10]. Вязкоупругое взаимодействие данных частиц в модели при этом отключается. Обозначенная особенность моделирования позволяет воспроизвести первоначальное связанное состояние почвы и её способность к фрагментации (разделению на отдельные комья). Также необходимо предусмотреть возможность имитации повторного «слипания» почвы, когда отделённые ранее элементы начинают притягиваться друг к другу при их контакте. При этом данное вторичное притяжение будет более слабым, чем ранее, когда почва была не разделена на фрагменты. В рамках такой модели можно с высокой степенью адекватности моделировать почвы с высоким содержанием влаги. Для расчёта сил, действующих на элементы, используется следующая методика. Каждый элемент i может испытывать силовое воздействие со стороны окружающих его элементов j :

^   N Ш ^     ~

F i =z ( F y + F j ),                          (2)

j = 1

• f У f В

где F ij и F ij — упругая и вязкая составляющие силы взаимодействия элементов i и j ;

И Ш — количество элементов грунта в модели.

Расстояние r j между центрами Si ( x , , yi, z i ) и Sj ( X j , y j , Z j ) каждой пары элементов можно рассчитать по теореме Пифагора (рисунок 1):

2      ,               . 2      ,              -.2

r j = V ⁽ X - ^Xj ) ^{+ (} У ! - У j ) ^{+ (} X - ^Zj )

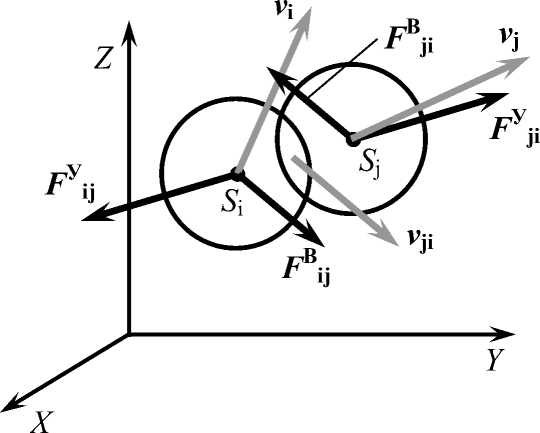
Рисунок 1. Вязкоупругое взаимодействие двух элементов грунта

Почвенные частицы, находящиеся на расстояниях r ij >  d_Э + d_M (где d_Э — диаметр элемента, d_M — расстояние притяжения), не взаимодействуют друг с другом ( Е У = 0 , F i^B = 0 ) (рисунок 1). При расстояниях, меньших суммы d_Э + d_M , упругие силы Е У рассчитываются следующим образом:

1) При r ij <  d э:

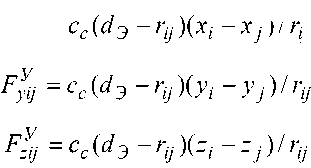
x j )/ri

2) При d э <  r ij < d э + d м/2:

F yij    c c ( dЭ r ij )( У i   y j )/ r ij ;                                  (4) F zij = c c ( dЭ - r ij )( zi - zj )/ r ij • F j = c ( d э - r ij )( x i - x j ) / r ij ; F yij = c ( d Э - r ij )( У i - У j )/ r ij ’                                  (5) F zij = c ( dЭ - r ij )( zi - z j ) / r ij •

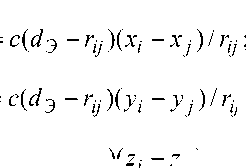
3) При d Э + d М /2 <  r ij <  d Э + d М :

F Xij = c ⁽ r ij - ( ^d э ^{+ d} м )) • ( x - ^xj )/ r j ;

F yij = c ⁽ rij - ⁽ d Э + d М )) • ⁽ y i - y j )/r ij ^;                             (6)

^Fyj = c ⁽ r ij - ^{( d}Э ^{+ d}М )) • ^{( z}i - ^zj )/ r ij •

• У У У                                г У

• Здесь Fxij , Fyij, Fzj — декартовы составляющие силы Fj ;

c — величина жёсткости упругого взаимодействия почвенных элементов, которая может принимать два значения: с = c_c , если элементы i и j связаны; с = с р , если элементы i и j не связаны.

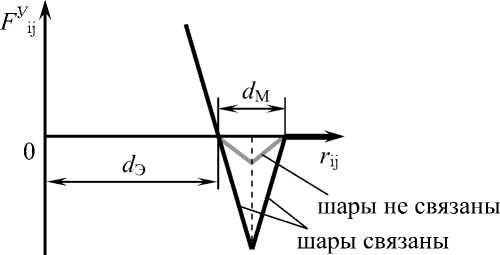
Рисунок 2. Влияние расстояния между двумя элементами i и j на модуль упругой составляющей силы взаимодействия

г У

Для ускорения интегрирования уравнений движения (функция Fj (r)) при реализации модели необходимо не допускать разрывов в области изменения расстояния между центрами г У пары шарообразных частиц. Поэтому при выборе характера зависимости Fij (r) на интервале dЭ + dM / 2 < rij < dЭ + dM целесообразно использовать зеркально отражённую относительно вертикальной прямой ветвь той же функции из интервала dЭ < rj < dЭ + dM / 2.

Декартовы составляющие вязких сил, с которыми взаимодействуют элементы, определяются следующим образом:

^FXij = k В ⁽ rij ^{- ( d} Э ^{+ d}М )) • ⁽ vxi ^- v xj ) ^;

^j = k В ⁽ r ij ^{- ( d}Э ^{+ d}М )) • ⁽ v yi ^- v yj ^{) ;}                           (7)

FBj = kВ (rij - (dЭ + dМ )) • (vzi - vzj ) , где vxi, vyi, vzi и vxj, vyj, vzj — декартовы составляющие скоростей i-го и j-го элементов; кВ — коэффициент вязкости.

Общеизвестно, что вязкая сила взаимодействия прямо пропорционально зависит от скорости движения тела в среде перемещения. Для учёта данной закономерности в модель необходимо ввести дополнительный коэффициент ( r ij - ( d э + d_M )), характеризующий взаимный контакт почвенных частиц друг с другом, определяющий торможение элементов при их взаимодействии.

Принимая во внимание третий закон Ньютона, величина взаимодействия двух шарообразных частиц будет равна по модулю и противоположна по направлению:

Fj =- Fj(8)

Уравнения движения i -го элемента, записанные на основе второго закона Ньютона, выглядят следующим образом:

тэ ^ = Е ( F * + F^B j );

dt2

d2 У N3 V R тэ = Е (j j(9)

dt2

d z   NЭ У В тЭ = Е (Fzij + Fzij ) - m Ш g , dt2

где т_э — масса элемента; t — текущее время; N_э — количество шарообразных элементов; g — ускорение свободного падения.

Приведённые уравнения движения описывают изменение динамического состояния почвенной среды с течением времени.

Чаще всего элементы необходимо представить в виде крупных фрагментов (комья, пласты), поэтому возможность вращения отдельных частиц вокруг их центров при моделировании можно не учитывать.

Движение шарообразных элементов в рамках реализации математической модели рассматривается в прямоугольном параллелепипеде с размерами L X х L Y х L Z (рисунок 3). При проведении теоретических исследований элементы необходимо расположить в нижней части параллелепипеда в несколько слоёв, для чего производится их встряска и происходит осаждение под действием сил тяжести.

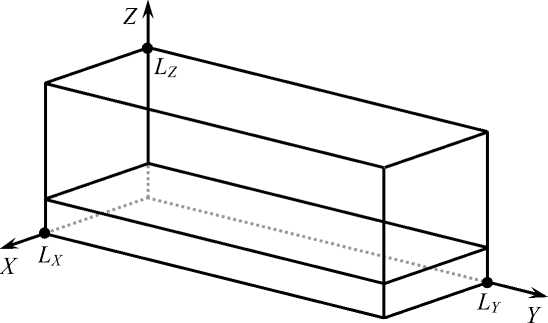
Рисунок 3. Параллелепипед L X х L Y х L Z , в котором отслеживается движение шарообразных почвенных элементов

Движение лесной машины необходимо задать вдоль направления OY . После прохода почвообрабатывающего орудия, вследствие взаимодействия рабочих органов с частицами из объёма почвенных элементов и их последующего отделения, образуется борозда.

Если элементы почвы контактируют со стенками параллелепипеда, то выполняется одно из условий: x i < 0, y i <  0, y i > L Y , z i <  0, z i > L Z . В этом случае элемент возвращается в параллелепипед от противоположной стенки. При выполнении условия y i >  L Y координате yi элемента присваивается значение y i = L Y - (y i - L Y ) и изменяется знак его скорости в направлении OY : v_yi = - v_yi .

Диаметр элементов d э оказывает непосредственное влияние на адекватность моделирования почвы, поэтому данный параметр целесообразно задавать как можно меньше. В то же время с уменьшением диаметра количество шарообразных частиц почвенной среды Nэ резко возрастает, что приводит к необходимости увеличения количества уравнений для математического описания лесной почвы и, как следствие, времени расчёта на ЭВМ. Так, при уменьшении диаметра элементов в два раза длительность расчёта увеличивается более чем в 8 раз. Общее количество почвенных частиц при диаметре 3^7 см в модели составляет от 4000 до 7000, в зависимости от необходимой величины заглубления рабочих органов.

Для генерирования почвенного объёма необходимое количество элементов распределяется внутри параллелепипеда случайным образом. Производится интегрирование уравнений движения почвы (9). Под действием сил тяжести элементы, оседая, формируют слой почвы в нижней части параллелепипеда. Для создания уплотнения в интервале времени от 5 до 10 секунд имитируется встряска элементов — для этого их координатам ( x i , y i , z i ) сообщаются незначительные случайные смещения, которые постепенно гасятся и к концу данной процедуры элементы становятся неподвижными. В дальнейшем, в случае контакта с рабочими органами лесной машины, шарообразные частицы почвы приобретают определённые скорости движения.

В конце подготовки рабочего объёма производится процедура связывания почвенных элементов. Информация об этом впоследствии будет храниться в двумерном массиве K ( i , j ). Каждая ячейка ( i , j ) принимает значение «истинно», если элементы i и j контактируют, т. е.

r ij = d Э + d М .

В противном случае ячейка принимает значение «ложно». При реализации модели через определённое время проводится проверка связанности для каждой пары i … j по тому же условию (10). При моделировании несвязных почв связи между элементами отсутствуют.

При необходимости математического описания взаимодействия рабочих органов лесных машин со структурно-сложной почвенной средой, включающей корни растений, корневую систему в модели также целесообразно представить множеством сферических элементов, расположенных в геометрической области пространства, представляющей собой цилиндр — верхнюю часть корневой системы, плавно переходящий в корни конической формы.

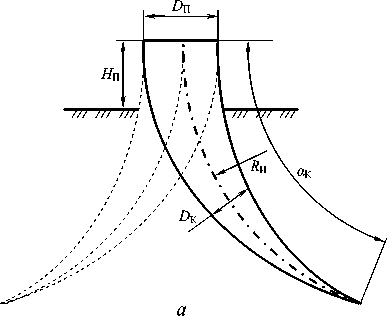
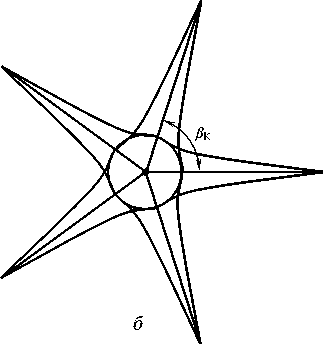
Рисунок 4. Расчётная схема к математическому описанию почвенной среды с корневыми включениями

Корневая система растения имеет сложную конфигурацию, поэтому она не может быть описана одним аналитическим выражением. Начальное размещение элементов внутри данного моделируемого объекта производится путём расположения с равным шагом вдоль осевых линий корней определённого количества базовых точек (например, для корневой системы с пятью корнями общее количество базовых точек составляет 500) [11]. Для корня, направленного вдоль оси x , это производится следующим образом:

x БТ_i = ~^+ + ^RИ cos ^a K (1 - cos ^а БТ ) ;

L_y у ^УБТ =—

;

z БТ_i = Z yn + H П ^{- R}И cos ^а К sin ^а БТ_i ;

^а БТ_i

i

= a-

^K 100

где x_БТ , y_БТ , z_БТ — координаты i -й базовой точки; L x , L y — длина и ширина пространства для моделирования в форме параллелепипеда; R И — радиус изгиба корня; а _к — угол, задающий длину корня (длина корня L k = R и • а к ); а БТ — угол расположения i -й базовой точки, измеряемый в той же системе координат, что и α К ; Z УП — вертикальная координата уровня почвы; H П — высота верхней части корневой системы над уровнем почвы.

Для размещения базовых точек вдоль остальных корней выражения (11) необходимо модифицировать:

x БТ, = ^ x + ^RИ cos ^а К ^{cos( e} K ^{( n}K ^- 1))(1 ^{- cos а} БТ ) ^;

ⁱ 2                                                                        ⁱ

L y

У БТ = — + ^RИ ^{cos а} К ^{sln( в} К ^{( n}K ^{- 1))(1 - cos а} БТ i ) ;

i 2

z БТ_i = Z yn + H П ^{- R}И ^{cos а} К ^{sin а} БТ_i ^;

i акт = а %---;

БТ i     K 100

вк = —, nK где βК — угловое расстояние между осями корней в горизонтальной плоскости; nK — номер корня (1, 2, ... NК); NК — принятое количество корней.

После того как базовые точки равномерно размещены вдоль центральных линий корней, выполняется размещение внутри корневой системы элементов древесины методом Монте-Карло. Для этого внутри модельного пространства многократно появляются элементы со случайными координатами — при этом проверяется, находится ли элемент вблизи какой-либо базовой точки корневой системы. Если расстояние между центром элемента до любой из базовых точек составит менее радиуса корня RБТi, данный элемент считается принадлежащим корневой системе. Иначе элемент «уничтожается» и производится генерация следующего. Процесс повторяется до тех пор, пока концентрация элементов в геометрической области, представляющей корневую систему, не достигнет необходимой равновесной концентрации.

4. Обсуждение и заключение

Представленная методика математического описания такого структурно сложного объекта, как лесная почвенно-растительная среда, в т. ч. и с наличием корневых включений, может быть использована в рамках моделирования работы лесохозяйственных агрегатов или сходных по технологическому процессу машин, рабочие органы которых при работе контактируют с почвой. Разработанная модель, в свою очередь, позволяет определить оптимальные значения конструктивных и технологических параметров проектируемых конструкций при создании высокоэффективных почвообрабатывающих технических средств.