Методика наблюдения малых движений поверхности лежащей капли в процессе ее испарения

Введение. Ранее нами была предложена методика [1, 2] наблюдения параметров формы капли в процессе ее испарения, обладающая высокой разрешающей способностью и безинерционно-стью. Она позволяет регистрировать изменение высоты капли с точностью до десятых долей длины волны света оптического диапазона ( X ~ 0,7 мкм) и определять радиус кривизны капли в ее вершине с точностью до долей процента. Разрешающая способность по времени этой методики ограничивается только быстродействием электроники и в наших экспериментах достигает величины порядка 10^–4 с. Все это дает возможность наблюдать гораздо более тонкие процессы, сопровождающие испарение капли, чем это возможно в традиционных экспериментах. К их числу относятся, например, следующие.

Во-первых, возникающее при испарении жидкости охлаждение ее поверхностных слоев приводит к развитию массообменных процессов как внутри лежащей капли (за счет естественной конвекции), так и на ее поверхности (за счет градиента поверхностного натяжения). Следствием является нарушение состояния механического равновесия и изменение формы капли. Капля, выведенная из состояния механического равновесия небольшим возмущением ее формы, стремится вернуться в него в процессе затухающих колебаний, параметры которых зависят от природы жидкости (вязкости, плотности, поверхностного натяжения) и условий опыта (свободная, висящая или лежащая капли) [3]. Во-вторых, несмотря на обычные в интерферометрии меры предосторожности, экспериментальная установка испытывает вибрации, вызванные многочисленными источниками механического шума, расположенными как внутри, так и за пределами лаборатории. Поэтому в процессе измерений нельзя исключить возможности возбуждения колебаний капли теми из этих источников, что имеют спектральные составляющие вблизи ее собственных частот. Тогда можно предположить, что капля, испаряющаяся или нет, всегда находится в состоянии колебаний, индуцированных этим шумом.

В настоящей работе делается попытка наблюдения процессов формоизменения капли, имеющих малую амплитуду и малый (по сравнению со временем испарения) временной масштаб, методами лазерной интерферометрии.

Эксперимент. Лежащая капля жидкости является оптическим объектом с фазовой отражающей поверхностью. Для нее необходимо определить изменение A h ( t ) = h (0) - h ( t ) высоты ее вершины как функции времени t в процессе испарения с точностью, достаточной для наблюдения малых колебаний, обусловленных причинами, рассмотренными выше или какими-либо другими. Ожидается, что частоты этих колебаний находятся в окрестности низших собственных частот колебаний лежащей капли, имеющих в наших экспериментах порядок 10² Гц.

Предлагаемый способ измерений состоит в следующем. Неразведенный вертикальный луч лазера после отражения от вершины осесимметричной лежащей (или висящей) капли имеет сферические волновые поверхности, поскольку в малой окрестности вершины поверхность капли можно считать сферической. Если это волновое поле наложить на когерентное ему опорное плоское волновое поле, возникнет интерференционная картина, изменение которой во времени обусловлено изменением A l оптической разности хода l между опорными и отраженными от капли лучами. Для центра интерференционной картины A l = 2 A h и поэтому связь наблюдаемой здесь интенсивности света с величиной A h имеет вид

I (t) = I (Ah (t)) = 11 +12 + 271112 cos I — 2 Ah (t) + 50 v X где 11,12 - интенсивности света в накладывающихся лучах света, 50 - разность фаз этих лучей в начальный момент времени, когда Ah = 0. Контрастная интерференционная картина получается, когда I1 = I2 = I0. Тогда можно написать

I ( t ) = I (A h ( t )) = 2 1 1 + cos — 2 A h ( t ) + 5 = 4 I _o cos² — A h ( t ) + 5 /2 . 0 I , X                0 ii 0 i X              0     )

За счет выбора начала отсчета времени можно положить 50 = 0. Удобно считать, что при t = 0 Ah (0) = 0. Тогда I (0) = 410, то есть время отсчитывается с момента, когда интенсивность света в центре картины достигнет своего максимума. Разрешая последнее уравнение относительно Ah(t), при выбранных начальных условиях можно написать

X

A h ( t ) =     arccos

2—

I ( t ) 4a; J

По этой формуле удобно оценивать A h на масштабах длины порядка X или долей X . На больших масштабах справедлива более простая оценка

X

A h ( t_n ) = n -.                                             (3)

где tn – время появления в центре интерференционной картины n -го максимума интенсивности света.

Схема натурного эксперимента, позволяющего реализовать обсуждаемый метод, подробно рассмотрена в работе [1] и воспроизведена на рис. 1. Здесь H – расстояние от подложки, на которой лежит капля, до фокальной плоскости объектива, B – расстояние от фокальной плоскости объектива до места расположения фотоэлемента, который регистрирует интенсивность света в центре интерферограммы, h – высота капли, f – длина фокусного расстояния объектива. Отме- тим, что линза, отражением от поверхности которой создается опорное поле, позиционирована по отношению к объективу таким образом, что формирует в плоскости регистрации интерферо- граммы плоский волновой фронт.

Отличия настоящего эксперимента от описанного в [1] состоят в следующем. Для увеличения скорости регистрации опытных данных в центре интерференционной картины вместо ПЗС-матрицы установлен фотодиод ФД256 с полосой светочувствительности 500– 1200 нм. Входная диафрагма, установленная перед фотодиодом, имеет диаметр 1,2 мм, что при выбранных нами геометрических параметрах оптической схемы позволяет фиксировать данные с участка поверхности капли диаметром около 10 мкм. Фотодиод подключен на вход операционного усилителя по схеме, снижающей синфазные помехи. В дальнейшем полученный сигнал усиливался вторым операционным усилителем

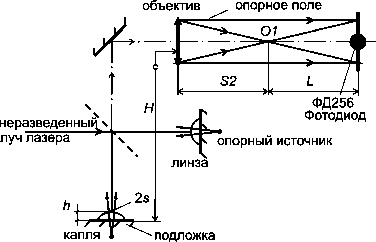
Рис. 1. Оптическа^ схема эксперимента по наблю^ению картин интерференции от вершины испар^ющейс^ капли

с регулируемым коэффициентом усиле-

ния. На выход этого усилителя подключен АЦП Е14-140 фирмы L-Card, позволяющий регистрировать на компьютере данные об интенсивности в центре интерференционной картины с часто-

Ушаков В.Л., Пызин Г.П., Бескачко В.П.

Методика наблюдения малых движений поверхности лежащей капли в процессе ее испарения той 100 кГц в динамическом диапазоне 14 бит. В экспериментах использовался He-Ne лазер ЛГН-215 с длиной волны X = 632,8 нм. Представленная схема позволяет уверенно регистрировать колебания поверхности капли с амплитудой, начиная от 20-40 нм, и частотами до 5 кГц.

В экспериментах изучались капли дистиллированной воды с массами 0,05-0,10 г, помещенные на подложку из стекла. Испарение происходило в объем лаборатории, где поддерживалась температура около 20 ° С и относительная влажность 50 %. В ходе эксперимента регистрировалась интенсивность I(t) в центре интерферограммы с частотой 100 кГц на временных интервалах до 10 мин. На рис. 2 приведен пример зависимости I(t) в эксперименте с испаряющейся каплей воды. На выносках в увеличенном виде показаны фрагменты этой зависимости, дающие представление о статистическом характере данных в области минимумов и максимумов интенсивности. Частота следования полос интерференции, f ucn , зависит от скорости испарения капли и в условиях описываемых опытов составляла величину f ucn - 1 Гц. На рис. 3 приведен пример зависимости Ah(t), полученной с помощью (3). Сравнение этой зависимости с линейной аппроксимацией ее начального участка показывает, что поведение Ah (t) может заметно изменяться на временных интервалах порядка десятков секунд.

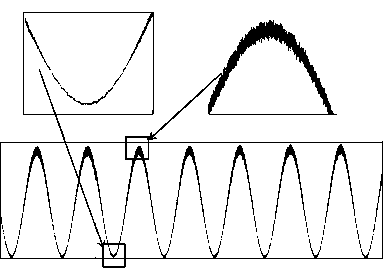
Рис. 2. Интенсивность света в центре интерференционной картины как функци^ времени, полученна^ в эксперименте с испар^ющейс^ каплей во^ы

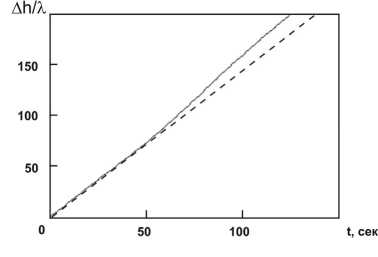
Рис. 3. Зависимость уменьшения A h/X высоты вершины испар^ющейс^ капли во^ы от времени. Пунктир – линей-на^ аппроксимаци^ начальной части зависимости

Наблюдаемую зависимость A h ( t ) можно связать c зависимостью от времени объема V ( t ) (или массы M ( t )) капли и со скоростью испарения v ( t ) = dM/dt . Используя методы, изложенные в работе [2], можно предварительно определить величину поверхностного натяжения о жидкости подгонкой решения уравнения Лапласа под наблюдаемые геометрические параметры капли: радиус кривизны в вершине капли R (0), ее высоту h (0) и радиус пятна смачивания r (0). Попутно становится известным профиль капли и ее объем V (0) в начальный момент времени. Заметим, что в экспериментах [2] обеспечивается условие r ( t ) = r (0) = const . Если теперь считать, что величина о не изменяется по мере испарения капли, то для определения формы и объема капли в следующие моменты времени нет необходимости находить радиус кривизны R ( t ) капли в вер-

шине, и эксперименты можно продолжить по схеме, описанной выше, определяя только высоту капли h ( t ) = h (0) -A h ( t ). Тогда V ( t ) можно найти, вновь решая уравнение Лапласа для каждого набора { о , r (0), h ( t ) } . На рис. 4 приведен пример зависимости V ( t ), найденной таким образом. Видно практически линейное уменьшение объёма капли в течении примерно часового интервала наблюдения.

Присутствие в эксперименте колебательных процессов проще всего выявить с помощью анализа Фу

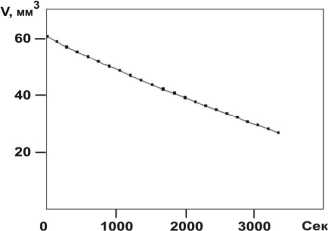
рье наблюдаемой функции интенсивности I(t). На   Рис. 4. График зависимости изменения объёма испар^ющейс^ капли от времени рис. 5, а приведен пример Фурье-спектра, полученно го для испаряющейся капли объемом 60 мм3. Богатая структура спектра означает присутствие многих источников колебаний: механических колебаний элементов оптической схемы (подложек, зеркал, объектива, детектора и т.п.), интенсивности излучения лазера, фоновой подсветки и пр. ^тобы определить, какие элементы спектра связаны с колебаниями поверхности капли, ака-кие имеют аппаратное происхождение, были выполнены эксперименты с «пустой» установкой, в которых капля отсутствовала. Результаты представлены на рис. 5, б. Сравнение рис. 5, а и б свидетельствует о том, что богатство спектральной структуры в опытах с каплей связано, в основном, с аппаратными причинами. Последующие эксперименты по измерению интенсивности падающего лазерного пучка от двух лазеров разных типов (гелий-неонового и полупроводникового) в интересующей нас частотной области выявили, в основном, колебания с частотой 50 Гц и кратными ей, обусловленные, очевидно, колебаниями напряжения в питающей лазеры сети (см. рис. 5, в). Это означает, что главными источниками аппаратного шума являются колебания использованных в опыте элементов оптической схемы, представленной на рис. 1. В связи с этим было решено упростить оптическую схему, оставив в ней минимум элементов.

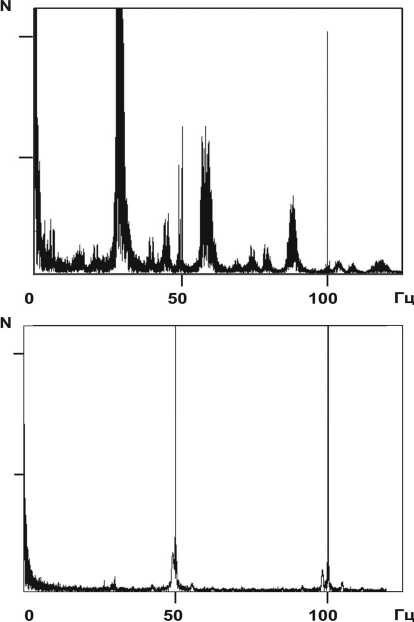
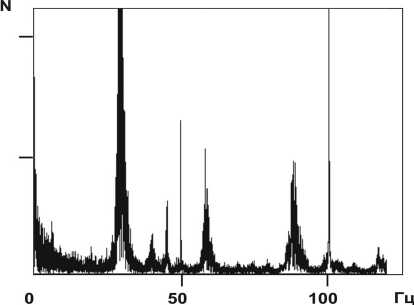
Рис. 5. Фурье-спектры интенсивности света I ( t ) :

• а)    в центре интерференционной картины в опыте с испаряющейся каплей;

• б)    в той же точке, что и на рис. 4, а , в отсутствие капли;

• в)    в падающем пучке гелий-неонового лазера ЛГН-215

Новая оптическая схема представлена на рис. 6 и включает два зеркала. После отражения в первом из них неразведенный луч лазера направляется вертикально на вершину лежащей капли, располагающейся на плоскопараллельной стеклянной пластинке (подложке). Затем формируются два сферических волновых поля: первое возникает после отражения луча лазера непосредственно от поверхности капли (предметное), второе (опорное) – после прохождения луча лазера сквозь каплю и его отражения от поверхности стеклянной подложки (нижняя часть подложки сделана матовой для предотвращения отражения от нее света). Длины когерентности используемого лазера оказалось достаточно для наблюдения устойчивой интерференционной картины в виде концентрических колец, в центре которой располагается фотодиод.

В новой оптической схеме нельзя получить информацию для расчета радиуса кривизны в вершине капли так же просто, как и в старой, поскольку здесь фаза не только предметного, но и опорного пучка зависит как от радиуса, так и от высоты испаряющейся капли. Это, однако, не является препятствием для наблюдения колебаний малой амплитуды (до 20–40 нм) с периодами, много меньшими чем характерное время существенного изменения формы капли, например, время ее жизни. На рис. 7 приведен спектр частот колебаний поверхности испаряющейся капли вблизи ее вершины, полученный с использованием газового лазера ЛГН-215. Видно, что изменения в оптической схеме эксперимента позволили избавиться от большинства паразитных колебаний. В диапазоне 10÷100 Гц присутствуют только колебания с частотами, кратными частоте электрической сети, и два парных пика малой мощности на частотах 29 и 48 Гц, отсутствующие в спектре излучения этого лазера (см. рис. 5, в ). Эксперименты с полупроводниковым лазером в

Ушаков В.Л., Пызин Г.П., Методика наблюдения малых движений Бескачко В.П. поверхности лежащей капли в процессе ее испарения том же и в более широком частотном диапазоне (до 103 Гц) также не выявили каких-либо заметных колебаний, которые можно было бы связать с каплей. Таким образом, при указанных усло- виях опытов не удается обнаружить колебательных процессов на поверхности капли с частотами

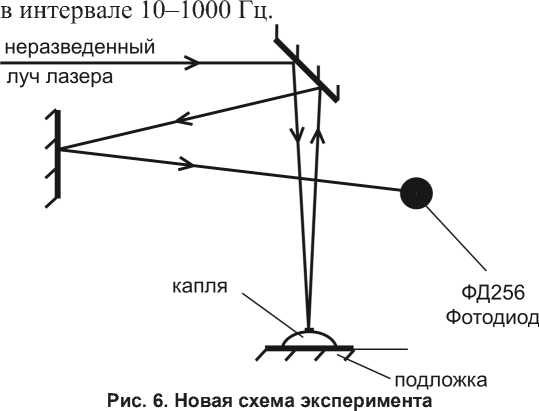
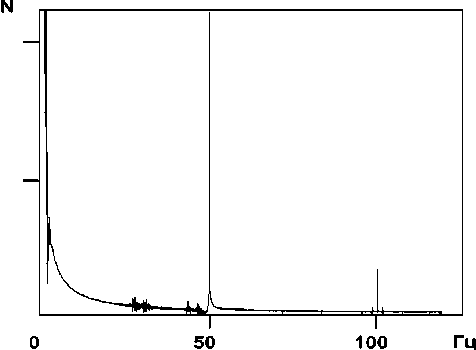
Рис. 7. Фурье-спектр I ( t ) в эксперименте с испар^ющейс^ каплей при использовании газового лазера ЛГН-215

Типичный вид спектра в низкочастотной области, вблизи частоты fucn (~2 Гц), показан на рис. 8.

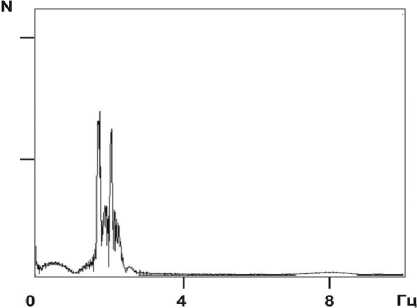
Рис. 8. Фурье-спектр I ( t ) в области низких частот вблизи f .

исп

f _исп , Гц

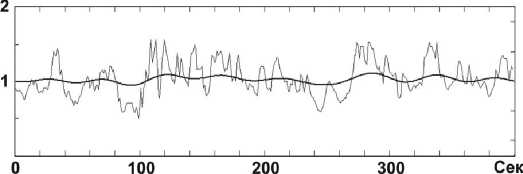
Рис. 9. Зависимость частоты сле^овани^ полос интер ференции, f_исп , от времени.

Гла^ка^ крива^ – результат Фурье-фильтрации.

Видно, что пик, отвечающий этой частоте, имеет сложную структуру и занимает целый диа пазон шириной ^fucn ~ 1 Гц, определяемый диапазоном скоростей, с которыми движется верши на капли в процессе испарения на отрезке времени, в котором за ней велось наблюдение. Пример того, как изменяется fucn с течением времени, приведен на рис. 9. Видно, что эта функция ведет себя довольно нерегулярным образом, а ее вариация имеет порядок ее среднего значения. Гладкая кривая на этом рисунке представляет собой попытку выделить в fucn (t) регулярную состав ляющую с помощью процедуры Фурье-сглаживания. Происхождение случайной и гладкой периодической составляющих нуждается в дальнейшем исследовании.

Заключение

Предложенная ранее [1] оптическая схема для регистрации параметров лежащей капли методами лазерной интерферометрии исследована с целью обнаружения малых движений на поверхности раздела жидкость — газ в процессе испарения, вызванных как самим процессом испарения, так и сейсмическими шумами различного происхождения. Спектральный анализ временных зависимостей интенсивности света в центре интерференционной картины, выполненный с помощью различных способов ее наблюдения, показал, что большая часть спектральных деталей связана с вибрацией элементов оптической схемы, а также с модуляцией интенсивности излучения лазеров промышленной частотой, на которой работают их источники питания. Предложена схема экспериментов, позволяющая свести к минимуму влияние элементов оптической схемы за счет уменьшения их числа до минимально возможного. С ее помощью проведены исследования испаряющихся капель воды с массами 0,05-0,10 г и показано, что в частотном диапазоне от 5 до 103

Гц волновые процессы на их поверхности отсутствуют. В области более низких частот имеется широкий пик со сложной структурой, расположенный вблизи частоты f ~ 2 Гц и отвечающий движению поверхности капли вследствие ее испарения, а также пик вблизи f ~ 0, указывающий на медленные движения поверхности с периодом в десятки секунд. Интерпретация этих деталей спектра требует дальнейших исследований.