Методика обоснования пространственных характеристик лазерного луча систем телекоммуникации при вхождении в связь с воздушными объектами управления

Цитирование: Калинин, В.С. Методика обоснования пространственных характеристик лазерного луча систем телекоммуникации при вхождении в связь с воздушными объектами управления / В.С. Калинин, А.А. Козирацкий // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(3). С. 338-349. DOI: 10.17516/1999-494X-0225

Целью настоящей статьи является разработка методики оценки эффективности вхождения в связь, учитывающей точность нацеливания лазерного луча на приемник и флуктуационные характеристики излучения лазера, позволяющей увеличить дальности действия лазерных систем телекоммуникации (при сохранении требуемой достоверности передачи информации) за счет оптимизации угла расходимости передающего лазерного средства.

В качестве показателя эффективности приема лазерного излучения примем вероятность вхождения в связь Р св .

Установление связи в системе телекоммуникации будет зависеть от выполнения двух совместных событий: события A _ь состоящего в том, что в результате нацеливания лазерный луч передающего средства будет ориентирован на апертуру приемника и «накроет» ее, и события A ₂, состоящего в том, что интенсивность лазерного излучения на входе приемника превысит порог обнаружения при сохранении требуемой достоверности приема информации [7]. Необходимо заметить, что накрытие апертуры приемника будет зависеть от расходимости лазерного луча передающей системы, расстояния, на котором находится приемник, и ошибки нацеливания, и не будет зависеть от интенсивности лазерного излучения на входе приемника. В свою очередь, превышение порогового значения интенсивности лазерного излучения на входе приемника или обнаружение будет зависеть от интенсивности излучения на выходе лазера передающего средства, длины трассы распространения излучения (расстояния до приемника) и суммарного ослабления при ее прохождении в атмосфере. Таким образом, можно утверждать, что рассматриваемые события независимы, поэтому вероятность вхождения в связь определим выражением [8]

Р св = P ( A • A ) = P ( A 1 ) • P ( A 2 ),                                                 (1)

где P ( A 1 ) - вероятность события, состоящего в том, что в результате нацеливания лазерный луч передающего средства будет ориентирован на апертуру приемника и «накроет» ее (вероятность нацеливания); P ( A ₂) - вероятность обнаружения сигнала в шумах.

Нацеливание лазерного луча системой телекоммуникации

Рассмотрим ситуацию, когда приемопередающие лазерные системы осуществили поиск и достигли ориентации в требуемом направлении (т.е. направлены друг на друга). При этом нацеливание лазерных лучей произведено с некоторой ошибкой.

На рис. 1 представлены поперечные сечения лазерного луча (пучка) двух приемопередающих систем «А» и «В» радиусом an и ап в плоскостях формирующих оптических систем приемников, точки Q и Q' определяют их центр, а точки О и O' являются центрами апертур ■ оптических систем приемников радиусом anp и а . Расстояние между точками Q (Q') и О р

( О' ), определяемое как р ош = a n - a np , характеризует ошибку нацеливания передатчика на приемник.

На практике в большинстве случаев ошибки нацеливания подчиняются закону Рэлея [8], поэтому

_ Р ш

W h ( Р ош ) = '’ e ' ,                                                                     (2)

° х

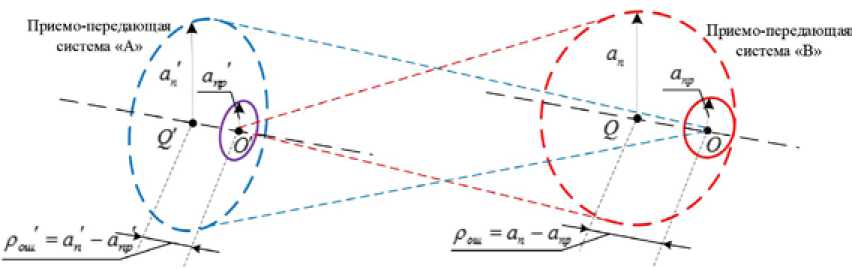
Рис. 1. Геометрия задачи

Fig. 1. Task geometry где σl – линейная среднеквадратическая ошибка нацеливания лазерного луча.

Для малоуглового приближения σ_l ≈ σ_αL , где σ_α – угловая среднеквадратическая ошибка нацеливания лазерного луча, L – дальность между передающей и приемной системами.

В этом случае вероятность нацеливания лазерного луча на апертуру оптической системы приемника определим выражением ап -апр                                      - (ап -апр )2

Р н = Р ( Л , ) = J W h ( Р ош ) d P ош = 1 - e     ■ .                                (3)

На рис. 2 представлены графики зависимости вероятности нацеливания P ( A , ) от радиуса поперечного сечения луча α_n в плоскости апертуры приемника при различных значениях ошибки нацеливания σ l , построенные с использованием выражения (3) для типового радиуса апертуры приемника α_np = 0,05 м.

Анализ графиков, представленных на рис. 2, позволяет сделать вывод о том, что с увеличением расходимости лазерного луча вероятность нацеливания (накрытия апертуры приемника) увеличивается, однако с увеличением расходимости излучения плотность потока мощности

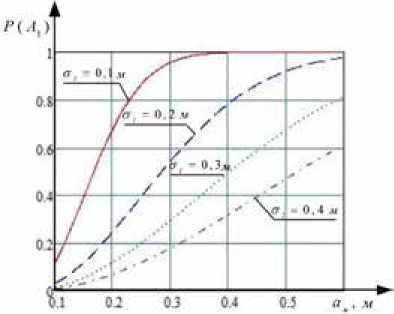
Рис. 2. Графики зависимости вероятности P ( A , ) от радиуса поперечного сечения луча a n

Fig. 2. The plot of the probability P ( A , ) of the radius of the cross section of the beam a n

Таблица 1. Результаты расчета оптимальных параметров и характеристик

Table 1. The results of the calculation of optimal parameters and characteristics

Значение угловой среднеквадратической ошибки наведения σα, рад Дальность L, м Значение линейной среднеквадратической ошибки наведения σl, м Оптимальный радиус луча а* м Угол расходимости ар,рад 2∙10–5 5^103 0,1 0,26 1,7-10-4 10^103 0,2 0,5 10-4 15403 0,3 0,7 9^10—5 20^103 0,4 0,9 0,9∙10–5 излучения на входе приемника уменьшается, таким образом, приемная система не обеспечит прием информации или обеспечит с низкой достоверностью. На этих графиках также видно, что при известной угловой среднеквадратической ошибке нацеливания подсистемы наведения σα для различных дальностей от передающей до приемной системы L возможно определить оптимальный (необходимый и достаточный) радиус поперечного сечения луча an и оптималь

*

ныи угол расходимости лазерного луча а , обеспечивающие вероятность нацеливания Р„ = 0,9. р ^,                                                                                            н ^,

Результаты расчетов приведены в табл. 1.

Оценка распределения интенсивности лазерного излучения на входе приемной системы

Пусть лазер передающего средства работает в режиме значительно выше порогового (^>>0). В этом случае, как показано в [4], плотность распределения интенсивности при генерации лазера имеет форму гауссовской плотности со средним значением J = ^[n J ПГ :

w ^{( J} изл ) =

^{n J} ПГ

exP 1 —

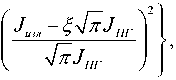
J ^ 0,

где JПГ – средняя пороговая интенсивность генерации лазера; ξ – параметр, изменяющийся в зависимости от режима работы лазера (значительно ниже порога генерации до нуля вблизи по- рога и до большого положительного значения), который, в свою очередь, зависит от значений средней пороговой интенсивности генерации лазера.

Интенсивность лазерного излучения в поперечном сечении луча в области апертуры приемной системы определим выражением:

Т = Т а 0- -" “L ^L

J пр J изл 2 e ,                                                                              ⁽⁵⁾

п где а о - начальный радиус луча на выходе передающего средства; a z - коэффициент суммарного ослабления потока излучения в атмосфере за счет рассеяния и поглощения [9, 10].

При этом необходимо отметить, что измеряемая с помощью, например, дальномера или спутниковой подсистемы GPS приемопередающих систем дальность L является случайной величиной, так как определяется с ошибками.

Выделим из выражения (5) Jизл, получим ап p«l L J

J изл ⁽ J пр ) 2 e J пр ^- а 0

Плотность распределения интенсивности лазерного излучения на входе приемной системы w ( J_np ) определим с использованием метода функционального преобразования случайных величин [8]:

^{w ( J} пр ) = w ^{( J} u™ ^{( J} пр )) •

dJ пр

Найдем производную выражения (6), получим dJ изл

dJ пр

- а» a l l

2 e а 0

-

Тогда на основе выражений (4), (6) и (8) распределение интенсивности флуктуирующего лазерного излучения на входе приемной системы запишем в следующем виде:

w ( J пр ) =

1  а2 e“L L nJПГ а 0

exp < -

Г „2                    \

-5^^L J пр - Ы^ пг а 0

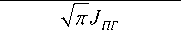
На рис. 3 представлены графики зависимости распределения интенсивности флуктуирующего лазерного излучения w ( J_np ) от нормированной величины k = J_np / J_nr при различных значениях радиуса поперечного сечения луча α n , построенные с использованием выражения (9). Характеристики передающего средства и типовые условия распространения лазерного излучения приведены в табл. 2.

Анализ графиков, представленных на рис. 3, позволяет сделать вывод о том, что изменение формы закона распределения существенным образом определяется расходимостью лазерного

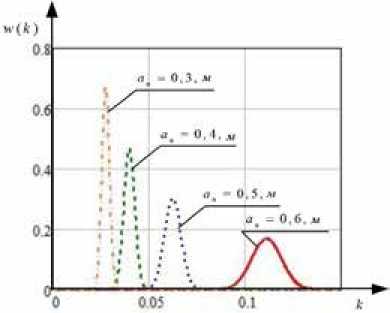
Рис. 3. Распределение интенсивности флуктуирующего лазерного излучения w ( J_np ) от нормированной величины k = J_np / J_nr при различных значениях радиуса поперечного сечения луча a n

Fig. 3. The distribution of the intensity of fluctuating laser radiation from w ( J_np ) the normalized value k = J_np / J_nr for various values of the radius of the beam cross section α n

Таблица 2. Характеристики передающего канала и условия распространения лазерного излучения

Table 2. Characteristics of the transmission medium and conditions for the propagation of laser radiation

Характеристика (параметр), единица измерения	Jnr , Вт / м 2	D , м	a о ~ D /4, м	ξ	L , м	α Σ , м
Значение	300	0,1	0,025	10	104	10-5

Таблица 3. Характеристики передающего канала и условия распространения лазерного излучения

Table 3. The results of the calculation of optimal parameters and characteristics

Характеристика (параметр), единица измерения Jnr, Вт / м2 θ, рад ап = 2 L^,м a0 ~ D/4, м L, м αΣ, м Значение 300 10-4 0,5 0,025 104 10-5 луча на входе приемной системы. При увеличении радиуса поперечного сечения луча an увеличивается дисперсия, максимальное значение плотности распределения при этом уменьшается, а среднее значение (математическое ожидание) увеличивается (распределение смещается вдоль оси абсцисс в область больших значений интенсивности флуктуирующего излучения).

На рис. 4 изображены графики зависимости распределения интенсивности флуктуирующего лазерного излучения w ( J_np ) от нормированной величины k = J_np / J_nr при различных значениях параметра ^, построенные с использованием выражения (9). Характеристики передающего канала и условия распространения приведены в табл. 3.

Проанализировав графики, выясняем, что с увеличением значения параметра ^ увеличивается среднее значение (математическое ожидание) и распределения смещается вдоль оси абсцисс в область больших значений интенсивности флуктуирующего излучения, не изменяя своей формы.

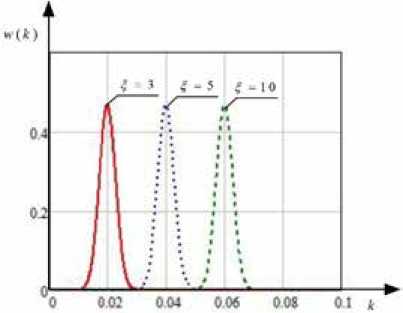
Рис. 4. Распределение интенсивности флуктуирующего лазерного излучения w ( J_np ) от нормированной величины k = J_np / J_nr при различных параметрах ^

Fig. 4. The distribution of the intensity of fluctuating laser radiation from w ( J_np ) the normalized value k = J_np / J_nr for various parameters ξ

Таким образом, на основе использования метода функционального преобразования случайных величин получено выражение распределения интенсивности флуктуирующего лазерного излучения на входе приемной системы.

Вероятность регистрации лазерного излучения средствами второго абонента

Вероятность обнаружения сигнала приемной системой определим следующим выражением:

Г

Р обн = Р ( А 2 ) = J w ( J пр Wпр ^, J п . о .

где J_n.o. – интенсивность порога обнаружения приемной системы.

Подставляя в выражение (10) закон распределения интенсивности лазерного излучения на входе приемной системы (9), получим:

обн

= 1-Ф

где Ф ( x ) =

2П

x - t 2

j e ² dt

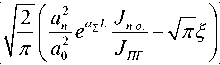
– интеграл вероятности.

На рис. 5 представлены графики зависимости вероятности обнаружения P ( A ₂) от радиуса поперечного сечения луча α n . Зависимости получены для значений интенсивности порога обнаружения J_n.o. = 100, 150, 200 Вт/м² с использованием выражения (11) и характеристик передающего средства, условий распространения лазерного излучения, приведенных в табл. 3.

Анализ графиков на рис. 5 позволяет сделать вывод о том, что при больших интенсивностях порога обнаружения приемной системы необходимо значительно уменьшить радиус поперечного сечения луча, следовательно, увеличить интенсивность мощности излучения, которая ограничена (постоянна). Одновременно уменьшение радиуса поперечного сечения луча в

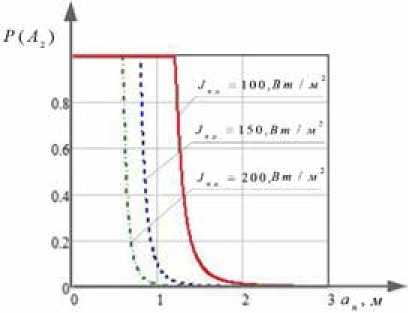
Рис. 5. График зависимости вероятности обнаружения P ( A ₂) от радиуса поперечного сечения луча α_n при различных значениях интенсивности порога обнаружения J_n.o.

Fig. 5. The dependence of the probability P ( A 2 ) of detection on the radius α n of the beam cross section for different values of the intensity of the detection threshold J n.o.

условиях существующих ошибок нацеливания может привести к неточной ориентации лазерного луча передающей системы на апертуру оптической системы приемника или «промаху».

Исследование эффективности вхождения в связь.

Обоснование рациональных пространственных характеристик лазерного луча системы телекоммуникации

Вероятность вхождения в связь определим в соответствии с выражением (1), подставляя в него полученные выражения вероятности нацеливания лазерного луча (3) на апертуру приемной системы и вероятности обнаружения (11), получим

P св

_ ⁽ а п -а пр ⁾²

2ст

_ e

1 _ф

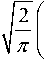
а п p ^ LL а 2

J^ - 4^^

JПГ

На рис. 6 представлены графики зависимости вероятности вхождения в связь Рсв(ап) от ра- диуса поперечного сечения луча αn при различных значениях угловых среднеквадратических Т нацеливания ,. на дальности L = 104 м

Как видно из представленных на рис. 6 зависимостей, с увеличением радиуса поперечного сечения луча α_n вероятность вхождения в связь увеличивается до определенного значения, что обусловливает увеличение вероятности нацеливания лазерного луча, а затем падает, что соответствует недостаточной интенсивности лазерного излучения для обнаружения на входе приемной системы. Поэтому можно сделать вывод о том, что существует оптимальное значение радиуса поперечного сечения луча a n , обеспечивающего максимальное значение вероятности вхождения в связь, при этом с увеличением точности нацеливания (уменьшении о_а ) вероятность вхождения в связь значительно увеличивается.

Для определения оптимального значения радиуса поперечного сечения луча исследуем выражение (12) на экстремум [11]. Найдем производную выражения (12) по параметру α_n и, приравнивая ее к нулю, получим:

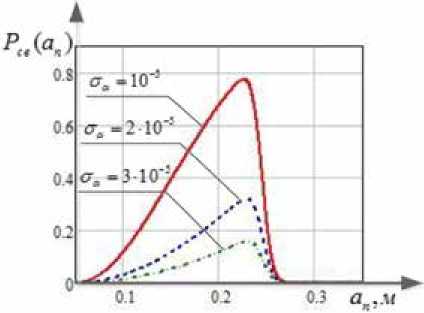
Рис. 6. График зависимости вероятности вхождения в связь Р_св ( a n ) от радиуса поперечного сечения луча α_n при различных значениях угловой ошибки наведения σ_α

Fig. 6. The dependence of the probability of joining Р_св ( a n ) the relationship on the radius a n of the beam cross section for various values of the angular pointing error σ α

/

1 - e

⁽ а п - а пр ⁾²

•

1 - ± ( J П_r + 1) erf [ x ] + ² J J ПГ exp { a _z L - x 2 } +

к

V

где erf [ x ] = -2= L x ² dx - функция ошибок, x = -X

ПI                        n

а

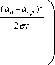
•[ 1 -ф[ V2 x ]]

= 0 ,

⁽ а п — а пр ) 2 ^

an Y a e

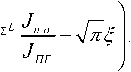
Данное уравнение является трансцендентным, решить его точными методами не представляется возможным [11], поэтому решим его численным методом и при заданных в табл. 2 характеристиках передающего канала и условий распространения лазерного излучения для типового радиуса апертуры приемной системы a_np = 0,05 м, интенсивности порога обнаружения j n_ ₀ . = 50 Вт/м² и линейной среднеквадратической ошибке нацеливания o i = 0,2 м получим *

корень уравнения an а 0,24 м.

Оптимальное значение угла расходимости излучения в общем случае а* будет определяться выражением [12]

. * р . ^а р = La n -

На рис. 7 изображены графики зависимостей Р св ( L ) от дальности при оптимальном значе-

*

нии угла расходимости излучения а_р = а_р и при a_p - const.

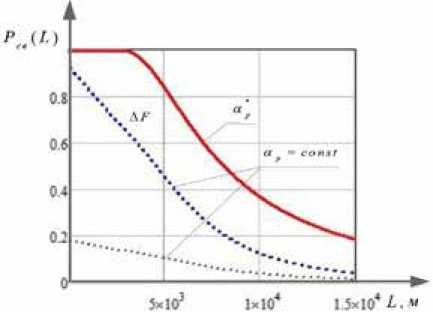
Рис. 7. График зависимости вероятности вхождения в связь Р_св ( L ) от дальности L

Fig. 7. The graph of the probability of joining the relationship Р св ( L ) from the range L

Как следует из данных графиков, формирование оптимального угла расходимости существенным образом повышает вероятность вхождения в связь. Так, на дальности 5 км за счет оптимизации угла расходимости вероятность P св повышается более чем в 1,8 раз и составляет величину 0,83.

Итак, в процессе исследования установлено, что при вхождении в связь двух приемопередающих систем в заданных условиях и наличии ошибки нацеливания существуют оптимальные характеристики передающего средства, при формировании которых вероятность вхождения в связь значительно повышается.

Заключение

Таким образом, на основе использования метода функционального преобразования случайных величин разработана методика оценки плотности распределения интенсивности флуктуирующего излучения лазера передающего средства на входе приемной системы, которая позволяет осуществлять оценку эффективности вхождения в связь с учетом точности нацеливания лазерного луча и флуктуационных характеристик излучения лазера передающего средства и обосновать основные требования к подсистеме наведения и формирования параметров лазерного луча бортовой телекоммуникационной системы.