Методика оценивания адекватности статистических имитационных моделей

Одним из основных способов получения знаний о сложных технических системах (СТС) является моделирование процесса их функционирования. Разнородность составных элементов СТС и разнообразие связей между ними, нелинейность различных свойств этих элементов обусловливают целесообразность применения для исследования таких систем имитационного моделирования (ИМ), выходными результатами которого являются два и более показателей, отражающих эти свойства.

Эффективность процесса получения знаний об исследуемой СТС зависит от качества ИМ, под которым понимается совокупность свойств, характеризующих их способность выполнять заданные функции. Одним из основных свойств модели, которое характеризует возможность по- лучения с ее помощью достоверных и точных данных об исследуемой СТС, является адекватность. Адекватность ИМ - это комплексное свойство модели, характеризующее степень соответствия значений выходных параметров модели и объекта с требуемой точностью при требуемой достоверности [1].

Если подходы к определению количественной оценки адекватности ИМ с одним показателем эффективности их функционирования хорошо известны [1–3], то подходы к оцениванию адекватности ИМ с большим количеством таких показателей по-прежнему требуют дополнительного исследования этого вопроса.

Одним из наиболее распространенных подходов к оцениванию адекватности ИМ является подход, представленный в [1, 2] и заключающийся в оценивании меры близости r результатов, полученных при моделировании ( М ), и результатов, полученных на основе обработки статистических данных, в которых содержатся сведения об исследуемом объекте ( ОЬ ):

r k ( Ob , M ) = | w Ob - w M |, k = 1^, (1) где w Ob - значение показателя к -го свойства СТС, полученное из статистических данных; И М -значение показателя к -го свойства СТС, полученное в результате ИМ ее функционирования; K -количество свойств, характеризующих СТС.

В качестве меры адекватности имитационной модели в этом случае выбирается вероятность

P [ r k ( Ob , M ) <  £ ] > 1 - 5 , (2) где £ - положительная величина, характеризующая точность модели; (1 - 5 ) - положительная величина, характеризующая достоверность модели, которую будем называть доверительной вероятностью и обозначать ее через в = (1 - 5 ).

В случае если СТС характеризуется только одним свойством, то такой подход является наиболее привлекательным. Однако если СТС характеризуется двумя и более свойствами или какое-либо свойство характеризуется несколькими показателями, то использование указанного подхода обусловливает необходимость для решения задачи оценивания адекватности ее имитационной модели получения свертки вероятностей (2) для каждого свойства СТС или для каждого показателя, характеризующего какое-либо свойство.

Еще один подход к решению задачи оценивания адекватности ИМ связан с использованием в качестве меры близости не расстояния (1), а расстояния между векторами, элементами которых являются значения показателей свойств СТС, полученные из статистических данных w ^Ob и при моделировании w ^M .

Для вычисления расстояния между этими векторами могут быть применены различные виды метрик, такие как метрики Евклида, косинусное расстояние, Чебышева, Хэмминга, Ли и др [4], что также привносит элемент субъективизма.

Как видим, оба рассмотренных подхода характеризуются высокой долей субъективизма в процессе оценивания адекватности ИМ. Приведённые обстоятельства обусловливают необходимость совершенствования научно-методического аппарата оценивания адекватности ИМ.

Целью данной статьи является представление методики объективного оценивания адекватности стохастических ИМ СТС.

В основе данной методики лежит представление выходных показателей модели в виде системы случайных величин (СВ). Тогда в качестве меры адекватности ИМ может быть использована вероятность

^£ 1 ^£ К

P [ ^r 1 ⁽ w Ob , И М ) <  ^£ 1 ,..., r k ⁽ w Ob , ^И М ) <  £ ,..., ^r K ⁽ W O ^b , ^ М <  ^£ K ] = J ... J f ^{( r} 1 , ^r 2 ,... ^r K ) d^r K ... dr , ⁽³⁾ 0 0

При этом модель будет считаться адекватной, если будет выполняться условие

P [ r 1 ⁽ w Ob ,И М ) < ^ 1 ,..., r k ⁽ w^Ob,w k? ) < £ k ,...,r K ⁽ w Ob ,w^M < £ k ]> 0 .             (4)

Предлагаемое авторами статьи использование в качестве меры адекватности ИМ вероятности (3), характеризующей вероятность достижения требований по точности каждого из рассматриваемых показателей, которая, по сути, является однозначно интерпретируемым объективным обобщенным показателем адекватности ИМ, позволяет избавиться от субъективизма при решении подобных задач оценивания, а также сохранить общепринятый физический смысл переменных E , в .

Обобщенная структурная схема методики, включающей в себя семь основных этапов, представлена на рис. 1.

_____      *      ______

Имитационная модель СТС

^1)Анализ статистических данных и формирование базы начальных характеристик процесса функционирования СТС с соответствующими им значениями показателей эффективности

н =

т

n

П 4

_______________________I_______________________

Имитационное моделирование процесса функционирования СТС

3) Нахождение наиболее вероятных значенийi выходных параметров модели и^"Д=1,А'

^) Нахождения расстояния по каждому критерию

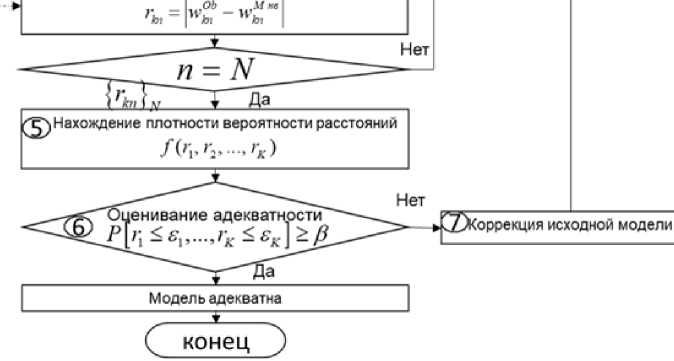
Рис. 1. Структурная схема методики оценивания адекватности ИМ

В качестве исходных данных для представленной методики используются данные, на основе которых синтезирована ИМ исследуемой системы, подлежащая оцениванию.

Рассмотрим более подробно содержание предлагаемой методики. На первом этапе необходимо осуществить ретроспективный анализ процесса функционирования реальной СТС, модель функционирования которой подлежит оцениванию с позиции ее адекватности. В результате такого анализа формируется база данных, содержащая сведения о начальных параметрах процесса функционирования СТС и наблюдаемых (измеренных) значениях показателей эффективности исследуемого процесса. Содержание такой базы данных может быть представлено в виде табл. 1.

Таблица 1

Результаты ретроспективного анализа процесса ф		ункционирования реальной СТС
№ наблюдения	Множество начальных параметров (исходных данных) процесса функционирования СТС	Показатели эффективности процесса функционирования СТС
1	V 1	w Ob , к = 1^
n	V n	w O , к = 1^
N	VN	w ON , к = 1^

Начальные параметры процесса функционирования СТС, заданные вектором V_n , будут в последующем использоваться в качестве входных параметров ИМ этого процесса. Поскольку на пятом этапе методики предполагается расчет плотности вероятности расстояний r , точность определения которой зависит от объема выборки этих расстояний, то целесообразно на первом этапе получить как можно большее количество наблюдений N .

Второй, третий и четвертый этапы методики связаны с проведением серии из I вычислительных экспериментов с ИМ c соответствующими значениями входных параметров V , нахождением по результатам моделирования наиболее вероятных значений всех рассматриваемых показателей эффективности функционирования w M нв , к = 1, K и получением N выборок расстояний ^{ r kn ^} .

Количество прогонов ИМ в каждом эксперименте необходимо определять, исходя из требуемого значения доверительной вероятности к результатам моделирования [5].

Необходимость использования для определения расстояний r_kn наиболее вероятных значений показателей, полученных в результате моделирования, обусловлена тем, что рассчитать средние значения показателей эффективности процесса функционирования реальной СТС для конкретного варианта начальных параметров этого процесса в большинстве случаев не представляется возможным вследствие малого количества наблюдений с одними и теми же начальными параметрами процесса. Поэтому, на наш взгляд, целесообразно использовать в качестве r_kn расстояние между случайными значениями показателей эффективности функционирования реальной СТС и наиболее вероятными их значениями, полученными в результате ИМ при одних и тех же исходных данных:

r kn = w Ob - w Mнв |, к = 1^.                               (5)

Для определения w^{M нв} необходимо по результатам ИМ получить плотности вероятности f n ( w M ). Значения w M , соответствующие максимальным значениям плотности вероятности, и есть наиболее вероятные значения каждого рассматриваемого показателя эффективности функционирования СТС. Для получения плотности вероятности можно использовать любой метод восстановления плотности вероятности по выборочным данным, например, метод ядерной оценки.

Последовательное выполнение основных этапов предлагаемой методики (с первого по четвертый этапы) позволит получить выборку расстояний { r_kn } N , представляющую собой систему K случайных величин, полученную в результате проведения N экспериментов. Данная выборка представляет собой исходные данные для пятого этапа методики , целью которого является получение плотности вероятности системы случайных величин f ( r 1 , r₂,..., r_K ).

В случае независимости отдельных СВ r , входящих в рассматриваемую систему СВ, плотность вероятности может быть получена как

K

f ⁽ r i , r₂,..., ^r_K ) = П ^fk ^{( r} k ).                                     ⁽⁶⁾

к = i

Однако использование выражения (6) возможно только после подтверждения гипотезы о независимости отдельных случайных величин, что в случае K > 2 связано с существенными вычислительными сложностями [6]. Поэтому целесообразно определять плотность вероятности f (r1, r2,..., rK) без предварительного определения факта зависимости или независимости случайных величин. Это может быть сделано с помощью метода восстановления плотности вероятности Парзена–Розенблатта [7–10]. При использовании этого метода в данном исследовании плотность вероятности f (r1, r2,..., rK) определялась согласно [11] по формуле f (ri

NK

.......   = IХП Г Y ( ),

N n = 1 k = 1 h k       h k

где r – реализация k -го расстояния в n -м опыте; h – ширина пропускания k -го расстояния;

_ X( r k ^— r kn ) 2

• Y ( r k—kn ) = — e ² h k — Гауссова ядерная функция.

• h k П

В работе [7] выражение (7) представлено в несколько другом виде, а именно по K выполняется суммирование, а не перемножение, как в данном случае. Однако, как показало данное исследование, такое выражение может быть использовано только для случая K <  2.

На шестом этапе предлагаемой методики необходимо путем K -кратного интегрирования полученной плотности оценить вероятность (3) и проверить выполнение условия (4).

Для вычисления кратных интегралов используются различные способы. Так, например, в [7] одно- и двукратное интегрирование осуществляется с помощью встроенных в пакет прикладных программ MATHLAB специализированых функций, а интегрирование более высокого порядка кратности предложено проводить с помощью вложенных интегралов. Однако использование такого способа для сложных подынтегральных функций сопряжено со значительными вычислительными затратами и характеризуется невысокой точностью, особенно для больших порядков кратности.

Проведенные исследования показали, что для определения вероятности (3) в данной работе целесообразно использовать метод численного интегрирования на основе применения метода Монте-Карло.

Сущность метода интегрирования на основе применения метода Монте-Карло заключается в том, что в случайно выбранных точках I -мерного пространства вычисляются значения подынтегральной функции, на основе которых определяется ее среднее значение. Значение интеграла при этом равно произведению среднего значения функции на объем тела, определенного числом этих точек [12].

Рассмотрим схему использования метода Монте-Карло для определения вероятности (3).

Шаг 1 . Определение количества экспериментов Q и количества точек J , по которым будет вычисляться интеграл в каждом эксперименте. Чем больше будет количество экспериментов и количество точек в каждом эксперименте, тем точнее будет результат определения вероятности (3). Однако большое количество экспериментов и точек в них может привести к существенному увеличению необходимых вычислительных ресурсов. Поэтому при определении этих параметров необходимо обеспечить требуемые значения показателей точности вычисления. Например, проведенные исследования показали, что для вычисления вероятности (3) для случая K = 3 c погрешностью А = ± 0.003 необходимо проведение 10 экспериментов с количеством точек в каждом J = 10 000.

x j = r kH + ( r k - r kH ) ^ , (8) где r_kн , r_kв - нижняя и верхняя граница интегрирования по r_k расстоянию соответственно; ^ -случайное число, распределенное по равномерному закону в интервале [0;1].

Так как rk = 0, rk = 8k , формула (8) преобразуется в xj = Ч^.                                      (9)

Шаг 3 . Вычисление значения функции (7) в каждой точке и определение ее среднего значения

J

Гср = ( Z f ( x q ,..., x j x^q Kj ))/ J .                           (10)

j = 1

Шаг 4 . Нахождение значения интеграла в каждом q -м эксперименте и вычисление значения вероятности (3) по формуле [12]

QK

P = (Z(П(rk -rk)))/Q,(11)

q=1

которая с учетом r k = 0, r k = 8 _k трансформируется в

QK

P = (Z (^ П £k))/Q.(12)

q=1

Использование изложенного метода позволит с высокой точностью оценить меру адекватности любых ИМ за счет возможности вычисления интеграла любой степени кратности.

Заключительной операцией шестого этапа методики является сравнение полученного значения вероятности (3) с требованием по достоверности в . В случае, если условие (4) выполняется, то разработанная модель обеспечивает требуемую степень адекватности. Если условие (4) не выполняется, то исходная ИМ подлежит коррекции ( этап 7 методики ) и процесс оценивания ее адекватности повторяется, начиная с первого этапа.

Представленная методика оценивания адекватности ИМ отличается от известных методик использованием в качестве обобщенного показателя адекватности – вероятности достижения выполнения всех требований по точности определения каждого рассматриваемого показателя эффективности СТС.

Таким образом, в рамках разработанной методики предлагается рассматривать адекватность имитационной модели, как комплексное свойство, характеризующее точность и достоверность исследуемой модели, и позволяющее избавиться от субъективизма при решении задачи многокритериального выбора при сравнении различных вариантов моделей заданной СТС.

Для наглядной иллюстрации представленной методики рассмотрим ИМ функционирования системы эксплуатации (СЭ) ракетно-космического комплекса (РКК) при проведении двух последовательных пусков ракет-носителей и оценим ее адекватность.

Выходными параметрами модели являются: продолжительность подготовки к пуску первой РН - t \_п ; продолжительность подготовки к пуску второй РН - t 2 _п ; стоимость функционирования СЭ РКК – С .

Входными параметрами являются параметры системы эксплуатации, заданные множеством V .

Требования к точности и достоверности выходных данных модели следующие:

• ^е 1 = ^е г = 1 ч. - требования к точности определения значений продолжительности подготовки к пуску первой и второй РН соответственно;

• 8 3 = 20000 у.е. - требования к точности определения значения стоимости функционирования СЭ РКК;

• в = 0,95 - требования к достоверности выходных параметров модели.

На первом этапе методики предполагается, что в результате ретроспективного анализа процесса функционирования реальной типовой СЭ РКК в течение 20 лет была получена база данных, содержащая сведения о начальных значениях ее параметров и наблюдаемых в последствии показателей эффективности процесса ее функционирования (табл. 2).

Таблица 2

На втором и третьем этапах для каждого набора входных параметров V n , n = 1,20 была проведена серия из 1000 вычислительных экспериментов с разработанной имитационной моделью, обработка результатов которых позволила получить для каждого n тройку наиболее вероятных модельных значений показателей эффективности функционирования СЭ РКК (рис. 2).

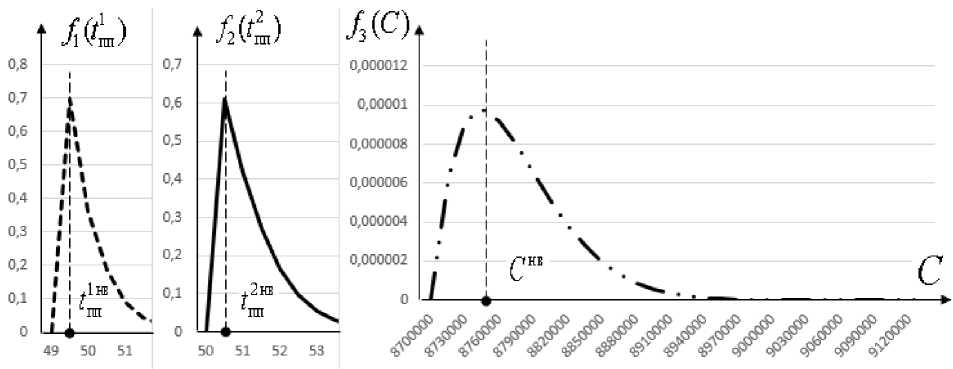
Рис. 2. Плотности вероятности и наиболее вероятные значения продолжительностей подготовки к пуску первой, второй РН и стоимости функционирования СЭ РКК при заданных значениях ее параметров из множества V

На четвертом этапе были получены выборки расстояний { r kn }₂₀, графическая интерпретация которых представлена на рис. 3.

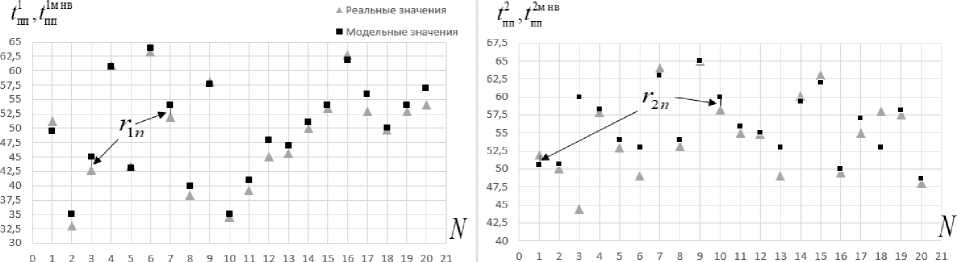
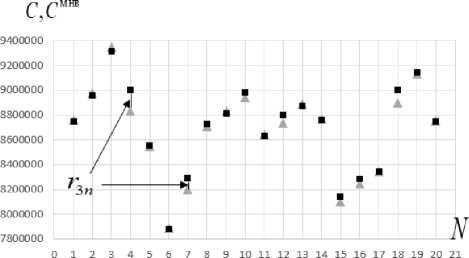
Рис. 3. Графическое описание множеств значений показателей эффективности функционирования реальной типовой СЭ РКК, полученных в результате ретроспективного анализа и вычислительного эксперимента

Результаты ретроспективного анализа процесса функционирования типовой СЭ РКК

№ наблюдения	Множество параметров СЭ РКК	Показатели эффективности процесса функционирования СЭ РКК
		t Пт , ч	4 , ч	С , у.е.
1	V 1	51,3	52	8760274
20	V 20	49	61	8730288

Далее на пятом этапе методики с помощью метода Парзена–Розенблатта и формулы (7) была рассчитана плотность вероятности f ( r 1 , r₂, r₃) :

1  20  3 i r - r

f(rl’r2’r3)=20 SOhY() ’ —1 k—1  k         k в результате трехкратного интегрирования которой по методу Монте-Карло получено значение вероятности удовлетворения требований к точности выполнения всех задач, стоящих перед моделированием

P [ ^r 1 ^ ^£ 1 , ^r 2 ^ ^£ 2 , ^r 3 ^ ^e 3 ] ^{— 0,96} .                                 ⁽¹³⁾

Поскольку значение вероятности P >  0,95, то можно сделать вывод, что разработанная ИМ функционирования СЭ РКК адекватна реальной.

Проведенные исследования позволяют сделать следующие выводы.

• 1.    Для всех применяемых в настоящее время методик количественного оценивания адекватности ИМ характерен существенный элемент субъективизма, следствием которого является сохранение неопределённости оценки.

• 2.    Предложенная в работе методика оценивания адекватности ИМ обеспечивает получение комплексной объективной оценки ее адекватности, отвечающей на вопрос: «С какой вероятностью будет обеспечена точность выполнения всех задач, стоящих перед моделированием».

• 3.    Предлагаемая в [7] формула (5) для построения плотности распределения случайных значений показателей качества функционирования СТС может быть применена только, если их количество не больше двух. При большем количестве рассматриваемых показателей необходимо пользоваться формулой (12), рекомендованной в [11].

• 4.    Для выполнения процедур кратного интегрирования, применяемых в предложенной методике для вычисления вероятности выполнения всех требований к обеспечению адекватности ИМ, целесообразно использовать процедуры интегрирования, основанные на использовании метода Монте-Карло.

Исследование выполнено за счет гранта Российского научного фонда (проект № 22-1900767,

• 1.    Микони, С.В. Квалиметрия моделей и полимодельных комплексов: монография / С.В. Ми-кони, Б.В. Соколов, Р.М. Юсупов. – М.: РАН, 2018. – 314 с.

• 2.    Вивчарь, Р.М. Риск-ориентированное управление созданием организационно-технических систем на основе использования имитационных моделей их функционирования / Р.М. Вивчарь, Б.В. Соколов, А.И. Птушкин // Вестник Воронежского государственного университета. Серия: Системный анализ и информационные технологии. – 2021. – № 2. – С. 17–31.

• 3.    Модель системы эксплуатации систем электроснабжения объекта повышенной опасности / А.Н. Степенко, Д.В. Решетников, Е.А. Андреев, А.А. Левчук // Современные наукоемкие технологии. – 2021. – № 11-2. – С. 289–293.

• 4.    Ростовцев, Ю.Г. Проблема обеспечения адекватности субъектно-объектного моделирования / Ю.Г. Ростовцев, Р.М. Юсупов // Известия вузов. Приборостроение. – 1991. – № 7. – С. 7–14.

• 5.    Вентцель, Е.С. Теория вероятностей / Е.С. Вентцель. – М.: Наука, 1969. – 576 с.

• 6.    Смирнов, Н.В. Краткий курс математической статистики для технических приложений / Н.В. Смирнов, И.В. Дунин-Барсковский. – М.: Физматгиз, 1959. – 436 с.

• 7.    Вивчарь, Р.М. Методика многокритериального оценивания эффективности функционирования стохастических сложных технических систем / Р.М. Вивчарь, Б.В. Соколов, А.И. Птушкин // Авиакосмическое приборостроение. – 2022. – № 7. – С. 3–14.

• 8.    Давыдов, В.С. Распознавание зарождающихся дефектов в узлах корабельных механизмов в результате вибродиагностирования на основе оптимальных решающих правил / В.С. Давыдов // Дефектоскопия. – 2019. – № 3. – С. 19–24.

• 9.    Поршнев, С.В. Использование аппроксимации Розенблатта–Парзена для восстановления функции распределения непрерывной случайной величины с ограниченным одномодальным за-

  коном распределения / С.В. Поршнев, А.С. Копосов // Научный журнал КубГАУ. – 2013. – № 92(08). – С. 1–27.

• 10.    Parzen, E. On Estimation of a Probability Density Function and Mode / E. Parzen // Ann. Math. Statist. – 1962. – Vol. 33, Iss. 3. – P. 1065–1076.

• 11.    Маркович, Л.А. Гамма-ядерные оценки многомерной плотности и ее частной производной по зависимым данным / Л.А. Маркович // Фундаментальная и прикладная математика. – 2018. – Т. 22, Вып. 3. – С. 145–177.

• 12.    Пармузина, М.С. Вычисление интегралов по методу Монте-Карло / М.С. Пармузина, А.А. Модебейкин, А.А. Суханов // E-SCIO – 2022. – № 6(69). – С. 553–565. https://e-

  scio.ru/?p=17881

Поступила в редакцию 1 июня 2023 г.

Bulletin of the South Ural State University

Series “Mathematics. Mechanics. Physics”

2023, vol. 15, no. 3, pp. 5–14

METHODOLOGY FOR ASSESSING THE ADEQUACY OF STATISTICAL SIMULATION MODELS

R.M. Vivchar1, A.I. Ptushkin1, B.V. Sokolov2

• ¹    Military Space Academy named after A.F. Mozhaisky, Saint Petersburg, Russian Federation

• ²    Federal State Budgetary Institution of Science “St. Petersburg Federal Research Center of the Russian Academy of Sciences”, Saint Petersburg, Russian Federation