Методика оценки частотных параметров сверхширокополосных сигналов с неизвестной формой спектра при наличии помех

На сегодняшний день непрерывно продолжающееся развитие новых радиоэлектронных систем требует повышения пропускной способности, а при передаче информации по беспроводному каналу расширения их возможностей и улучшения качественных характеристик. Одним из возможных путей решения этой проблемы является использование сверхширокополосных (СШП) сигналов [1–8; 10–13]. В связи с этим во многих прикладных задачах необходимо решать задачи оценки параметров СШП-сигналов [7; 10; 12; 13], в том числе задачи оценки частотных параметров СШП-сигналов. В работе [7] выполнены синтез и анализ квазиправдоподобного (КП) алгоритма оценки частоты СШП-квазирадосигнала с неизвестной длительностью, наблюдаемого на фоне гауссовского белого шума (ГБШ). В работе [10] выполнены синтез и анализ КП-алгоритма оценки средней частоты СШП-сигналов, принимаемых на фоне гауссовских узкополосных помех (ГУП) и ГБШ. В частности, существенный интерес вызывает задача совместной оценки центральной частоты и полосы частот СШП-сигналов с неизвестной формой спектра, принимаемых на фоне ГУП и ГБШ.

• 1.    Алгоритм оценки частотных параметров СШП-сигналов при наличии ГУП и ГБШ

Пусть на фоне ГУП и ГБШ наблюдается СШП-сигнал s ( t, Q i , Q 2 ), спектр которого можно представить в виде

[q(го), Qj < го < Q2, s (го, Q.,, Q,) = ^                                                   (1)

• ^{1    2}   l 0, ro1; ro>Q2.

Здесь обозначим: Q i - минимальная частота спектра; Q 2 - максимальная частота спектра; v= ( Q i +Q ₂ )/ 2 - центральная частота и Q = = ( Q 2 -Q i ) - полоса частот. Значения Q i , Q 2 могут принимать значения из априорных интервалов Q. еГО- • ;□ i = l,2.

i L i min ^; i max J ^{,       ,}

Используя такие параметры СШП-сигналов, как центральная частота v и полоса частот Q , спектр (1) можно переписать следующим образом:

s ( го , v , Q ) = q ( го ) I L ( ro -v ) QJ , где

I ( x ) =

i,

0,

I x < V² •

I x ² V² •

а v и Q могут принимать значения из соответ- ствующих интервалов:

v е Гv • : v      , Q e Fq • : Q 1.                 (3)

L min ’ max J ^, L min ’ max J ’

Тогда для принимаемого сигнала имеем

где

1 v+Q/2

s ( a , v , Q ) =           q (a) exp( j &  t) d a .

2n v—Q/2

T x (a) = J x (t )exp(—j at )dt

Полагаем, что на интервале времени L 0, T J наблюдается реализация x ( t ) = s ( t , v q , Q q ) + n ( t ) + ^ ( t ), где V q , Q q - истинные значения неизвестных центральной частоты и полосы частот; n ( t ) - реализация ГБШ с односторонней спектральной плотностью N q ’ Ь ( t ) - ГУП с корреляционной функцией B ^ ( 1 2 — 1 1 ). В частном случае спектральную плотность ГУП можно представить в виде [6; 10; 12]:

– текущий (выборочный) спектр реализации наблюдаемых данных.

Согласно [10], КП-алгоритм оценки центральной частоты V и полосы частот fl можно выразить через КП-алгоритм оценки минимальной fl 1 и максимальной fl 2 частот спектра: v = = (f l 1 +f l 2 )/2 и fl =Q 2 —fl 1 , согласно которому, необходимо найти оценки минимальной fl 1 и максимальной ff 2 частот спектра. В соответствии с [10; 14] находим КП-алгоритм оценки как

G ^ ^{( a )} = 2

I

\

a^ — a

^Ю 0 ^+a

Q, ь 7

где & о - центральная частота ГУП; Q ^ - ширина полосы частот ГУП; у - интенсивность ГУП.

Как известно [7; 10; 13], для оценки частотных параметров СШП-сигналов можем использовать КП-алгоритм оценки, согласно которому логарифм функционала отношения правдоподобия (ЛФОП) для некоторого ожидаемого сигнала (2) запишется в виде

T

L ( v , Q ) =         x ( t ) s .| ( t , v , Q ) dt —                               (6)

N1

T

—        s 2 ( t , v , Q ) dt .

N1

Здесь s i ( t , v , Q ) - опорный сигнал, причем в общем случае s ( t , v , Q ) ^ s i ( t , v , Q ). И находим КП-алгоритм оценки частотных параметров СШП-сигнала как ( v , fl ) = argsup L ( v , Q ).                                   (7)

Если реализация наблюдаемых данных x ( t ) не содержит ГУП Ь ( t ) и s ( t , v , Q ) = s i ( t , v , Q ), то оценка (7) является оценкой максимального правдоподобия (ОМП).

Полагаем, что у ожидаемого сигнала s i ( t , v , Q ) спектр подобен спектру СШП-сигнала (2) и может быть записан как

(f l 1 , fl 2 ) = arg sup L ( Q 1 , Q 2 ), Q

L ( Q 1 , Q 2 ) =----- I q 1 ( a ) x ( a ) d a —

^{П 0 Q} 1

q ₂

— 2 N J I q 1 ^{( a )}l² d "’

^{0 Q} 1

ЛФОП (11) можно представить в виде

L ( Q ₁ , Q 2 ) = L ₁ ( Q ₁ ) + L 2 ( Q 2 ),

₁ ^Q f

L ( Q 1 ) =       J q 1 ( a ) x ( a ) d a —

^{П 0 Q} 1

1 Q f

^— 2 N J q 1 ^{( a)}F ^{d a}

^{0 Q} 1

Q

L ( Q 2 ) =----- J q 1 ( a ) x ( a ) d a —

^П N ^{0 Q} f

Q ₂

— 2 N J q 1 ^ d ^{a 0 Q} i

Переходя (6) к спектральному представлению, получим

v+Q/2

L( v , Q ) =             q^ ( a ) x ( a ) d a —

nN       1

⁰ v—Q/2

—

v+Q/2

J q ₁ ( a )| d a , v—Q/2

где Q _f - произвольное фиксированное значение частоты из интервала [^Q 1max , ^Q 2 min J •

Как известно [15], гауссовские спектральные

меры на неперекрывающихся частотных интервалах ортогональны. Поэтому случайные процессы (СП) L 1 ( Q 1 ) (13) и L 2 ( Q 2 ) (14) будут статистически независимыми. В результате оценку (10) можно переписать как

Q i = arg sup L i ( Q i ), i = 1,2. (15)

Рассмотрим статистические характеристики СП L 1 ( Q 1 ) и L 2 ( Q 2 ), которые, согласно (13), (14), представляют собой линейные преобразования СП x ( a ) и, следовательно, являются гауссовскими. Для исследования статистических описаний

находим их математические ожидания

S. ( О, ) = L( ( Q.. )\ =----- п N

^Q f

J      |q ( ю ) q ₁ ( ю )| d ю- (16)

max(Q 1 ,Q ₀₁ )

+ p 2 g ( ° 0 i )min I 0,( - 1) i ( Q i -° 0 i ) I К + о ( Л ),

1   ° f

-            q₁ ( ю ) d ю ,

2 п N      ^{1   1}

^{0 Q} i

где g (ю) = q (ю)/ q1 (ю), p2 = 2 |q1(Q0 i )| 2 /n 0 п, i = 1,2,

а корреляционные функции (18) и (19) перепишем

в виде

S 2 ^{( Q} 2 ) = L 2 2 ^{( Q} 2)) =

^{1  п N} о

min(° 2 ,° 02 )

J      |q ( ю ) q ₁ ( ю )| d ю- (17)

^Q f

⁵ 1 ^{( Q} 11 , ^Q 21 ) = I ¹ +

I ^N 0.

^Q 2

-           q^ ( ю ) d ю

2 п N ¹

0 ^Q f

( - 1) ^Q ° ⁰¹,        ,2

n N- J ^{q ( ю)}1 ^{d ю}

^{0 Q} f

+

и корреляционные функции

+ p 2 min [ ( - 1)( Q 11 -Q ₀₁ );( - 1)( Q ₂₁ -Q ₀₁ ) ]/q ₀ ,

⁵ 2 ^{( Q} 12 , ^Q 22 ) = I ^{1 +} J

I ^N 0.

.  Q02

------ [ Iq, (ю)|2 dю п N       1   1

^{0 Q} f

+

5 1 ( 0 11 , Q 21 ) =

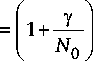
⁵ 2 ^{( Q} 12 , ^Q 22 ) =

1      ° f q., (ю)|2 dю пN                1   1

0 max(Q 11 ,Q ₂₁ )

min(° 12 ,° 22 )

-1- f     ^q ( “ I²

" ^N 0    O f

d ю

Согласно [6; 10], математические ожидания (16), (17) достигают максимума в точке Q 1 = Q 01 и Q 2 = ° 02 соответственно. Положения максимумов математических ожиданий (16) и (17) совпадают с истинными значениями минимальной и максимальной частот сигнала (4) при выполнении

условия

q 1 ( Q o i ) <  2 q ( ° о i ), i = 1,2.

Тогда КП-алгоритмы оценки (15) будут состоятельными.

Будем полагать, что отношение сигнал – шум (ОСШ) на выходе приемника достаточно велико, в этом случае положения максимумов СП L 1 ( Q 1 ) и L 2 ( Q 2 ) располагаются в малых окрестностях точек ° 01 и Q 02 , поэтому необходимо исследовать поведение СП (13) и (14) в окрестностях точек Q 01 и Q 02 . Полагая

Л = max { Q i - Q 0 i |, |q j - Q 0 j } ^ 0, i , j = 1,2, аппроксимируем средние значения (16) и (17) отрезками разложений Тейлора:

S i ( Q i ) = ( - 1) i

1 ^Q o i

J | q ( ю ) q 1 ( ю )| d ю .^{nN 0 Q} f

-

+ ^p 2 ^{min [ ( Q} 12 ^Q 02 ^{);( Q} 22 ^Q 02 ) ]/^Q 0 } ,

где p ² = 2 | q 1 ( Q 01 )| 2/1

N 0 п и

^p 2 = ² | ^q 1 ^{( Q} 02 )| /1

N 0 п .

Как следует из (20), (21) и (22), в малых окрестностях точек Q 01 и Q 02 СП (13), (14) является гауссовским марковским СП диффузионного типа с коэффициентами сноса и диффузии [16]:

k ₁₁

^k 12 =

2 n N 0

^Q0 i       2

J ^ 1 ( ю )| d ю

^Q f

^{- ( - 1)} i ^{p 2 ( Q} i ^-Q 0 i )/^{2 Q} 0 ⁺

p ² I ^g 1 , ^Q 1 > ^Q 01 , 2 Q ₀ 1- 1, Q 1 ₀₁ ,

p 2 | 1+— I

¹ 1    ^N 0 J

2 Q ₀     ^,

,      Р2 I g2, Q2 < Q02, k12 =      1          _

2 Q 0 1- 1, ° 2 > ° 02 ,

p 2 1 1+— I

=—,

²²       2 Q ₀

где g 1 = 2 g ( Q ₀₁ ) - 1 и g 2 = 2 g ( Q ₀₂ ) - 1.

Найдем совместную плотность вероятности распределений положений абсолютных максимумов реализаций СП L 1 ( Q 1 ) и L 2 ( Q ₂ )^:

W ( Q 1 , Q 2 ) = W _{1 Q} ( Q 1 ) W _{2 Q} ( Q 2 ),

где W 1Q ( Q 1 ) и W 2Q ( Q 2 ) — плотности вероятностей положений абсолютных максимумов реализаций

СП L 1 ( Q 1 ) и L 2 ( Q 2 ).

Далее найдем совместную плотность вероятности нормированных ошибок совместных оценок.

Пусть

H = p 2 g 1 ( Q 1 - Q 01 )/ 2, Ц 2 = p 2 g 2 ( Q 2 - Q 02 )/ 2

– нормированные ошибки КП-алгоритма оценки нижней и верхней частот сигнала (4). Тогда в слу-

чае, когда ОСШ на выходе приемника достаточно велико, получим асимптотические выражения для плотностей вероятностей нормированных ошибок в виде

[ w₀ (н/ g i)/ g i, н <  0,

Wh ) = 1

I g 1 W ₀ (H g 1), Ц 1 ^ 0,

, ,   [ g 2 W 0⁽^2 g 2 )> ^2< ⁰>

W 2 ( ц ₂ ) = 1

I W 0 ⁽ ^2/ g 2)/ g 2 , ^ 2 ^ ⁰

где

W ₀ ( x ) = 3 exp(2| x |)

1 -Ф

-

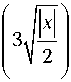
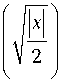
– предельная плотность вероятности нормированной ошибки ОМП одного параметра сигнала при условии, что второй параметр известен, g i , i = 1,2. Согласно [9], плотность вероятности (28) существенно отличается от гауссовской.

Согласно (25), (26) и (27), совместная плотность вероятности нормированных ошибок КП-

^{13 ( 1 +} q ^)Q 0 ^f g 1 ⁺ g -1 g 2 ⁺ g 21 ' =¹ .

⁽ P 1 P 2 ^{) 4} I g 2          g 2 J

Здесь q = у / N 0 - отношение помеха - шум.

Видно, что можно рассчитать значения смещений и рассеяний ОМП центральной частоты и полосы частот при g 1 = g 2 = 1 в условии отсутствия помех ( q = 0), и имеем

b(V| V0, Q0) = 0,

b(Q|v0 , Q0) = 0,

V (V| V0, Q0) =------07,

( P 1 P ₂ )

, -1        .52

V (Q^, Q0) =-----07.

( P 1 P ₂ )

2. Влияние ГУП на точность оценки частотных параметров СШП-сигналов

алгоритма оценки равна

W ( _Ц 1 , ц ₂ ) = W 1 ( ^ 1 ) W ₂ ( ц ₂ ).

Введем в рассмотрение нормированные ошибки КП-алгоритма оценки центральной частоты и полосы частот сигнала (4):

В качестве примера исследования рассмотрим опорный сигнал со спектром прямоугольной формы:

q1(ro) = a 1, принимаемый СШПС с прямоугольной формой спектра со скошенной вершиной:

П 1 = ( V —v ₀ ) Р 1 Р ₂ /Q ₀ ,                                (30)

П ₂ = ( Q -Q 0 ) p 1 p ₂/2 Q ₀ .                          (31)

q ( ro ) = a

1 _{+ 2} ^ro-V 0 f 1 - k "I Q ₀ ^ 1 + k J

Переходя в выражении (29) к новым переменным (30), (31), находим предельную двумерную плотность вероятности нормированных ошибок совместных оценок [14]:

W ( П 1 , П ₂ )

^g 1 ^g 2 _W

g ₁

П 1 -П

W ₂

g ₂

П + П 2

. (32)

Совместная плотность вероятности (32) позво-

ляет рассчитать асимптотические значения сме щений и рассеяний КП-алгоритма оценки V и Q:

b(V| v0 , Q0) = (V-v0} =

= 3 ( 1 + q ) ^Q 0 ⁽ g 1— ^{2 -} g 2 ²)/ 4⁽ P 1 P 2 ^{) 2} ,

b(Q|v0 , Q0) = (0-Q0} =

= 3 ( 1 + q ) Q 0 (2 — g 1 ^{- 2} — g 22 )/2( P 1 P 2 ) 2 ,

• V1(V| v0 , Q0) = ^(V -v0 )2^ =

• = ^{13 ( 1} + q ^)Q 0 ^f g 1 ⁺ g ^{- 1} + g 2 ⁺ g 21

• " 4(P1P2 )4 I   g2         g22

• V1(v| V0, Q) = {(Q-Q )2) =

Здесь параметры a , a 1 - интенсивности сигналов и k характеризует наклон вершины спектра СШП-сигнала.

В этом случае можно записать величины g1 и g2 как g 1 =[ k (4a-1) -1]/(1 + k), (41) g 2 = (4a- k -1)/(1 + k), (42) где a = aja 1 - отношение интенсивностей принимаемого и опорного сигналов.

Проигрыш в точности КП-алгоритма оценки по сравнению с точностью ОМП будем характеризовать отношением их рассеяний, которое можно записать как

V 1 ( V	— V 0 , Q 0 )   V 1 ( Q	V 0 , Q 0 )
V ( V	=    - V 0 , Q 0 )    V ( Q	V 0 , Q 0 )

< , -1 , -1

^g 1 ^{+ g} 1 . ^g 2 ^{+ g} 2

+FT

\ ^g 1 ^g 2 /

X =

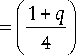
Здесь значения g 1 , g 2 определяются из (41), (42).

На рис. приведены зависимости проигрыша в точности КП-алгоритма оценки по сравнению с точностью ОМП (43) от параметра k , характери-

зующего наклон вершины спектра СШП-сигнала для различных значений отношения помеха – шум q при a = 1.

При анализе зависимостей, представленных на рис., видно, что в случае, когда значение к <  1, проигрыш в точности КП-алгоритма оценки уменьшается при увеличении значений k , характеризующих наклон вершины спектра СШП-сигнала, и проигрыш возрастает с увеличением значений k в случае, когда значение к >  1. Также увидим, что проигрыш в точности КП-алгоритма оценки возрастает с увеличением значений отношения помеха - шум q . Так, в случае, когда значение к = 1 рассеяние КП-алгоритма оценки больше рассеяния ОМП в 1,5 раза при q = 0,5, в 2,5 раза при q = 1,5 и в 3,5 раза при q = 2,5.

Заключение

Выполнены синтез и анализ алгоритма совместной оценки центральной частоты и полосы частот СШП-сигналов, принимаемых на фоне ГУП и ГБШ. Исследовано влияние ГУП на точность этой оценки, и показано, что точность оценки снижается с увеличением интенсивности помех.

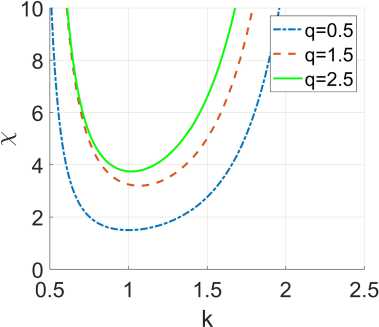
Рис. Зависимости проигрыша в точности КП-алгоритма оценки по сравнению с точностью ОМП от параметра, характеризующего наклон вершины спектра СШП сигнала

Fig. Dependences of the loss in accuracy of the quasi-likelihood estimate compared to the accuracy of the maximum likelihood estimate on the parameter characterizing the slope ofthe peak ofthe spectrum of the UWB signal

Полученные результаты позволяют сделать обоснованный выбор необходимого алгоритма оценки частотных параметров СШП-сигналов в зависимости от требований, предъявляемых к точности оценок в условиях сложной сигнальнопомеховой обстановки.