Методика оценки и оптимизации систем с учетом управленческих и организационных показателей эффективности

DOI:

Международные компании и организации должны конкурировать на глобальных рынках, где успех и выживание в значительной степени зависят от уникальных внутренних возможностей [1]. В настоящее время организации вынуждены повышать качество выпускаемой продукции и экономить затраты, чтобы оставаться конкурентоспособными [2]. На общий финансовый результат организации могут влиять многие параметры, которые классифицируются следующим образом: технологии, оборудование, менеджмент, персонал, правила и процедуры. Организационные и управленческие факторы имеют большое значение для эффективности производственных систем, и наоборот, поэтому необходим интегрированный алгоритм для продвижения и постоянной оценки эффективности управления. Проблемой в данном случае является необходимость правильно распознавать и классифицировать эффективные параметры, решению которой и посвящена данная статья.

Первым шагом для прогнозирования поведения организационной системы является необходимость провести выбор шкалы или показателя эффективности с учетом совместимости шкалы с целями системы управления, инвазивности измерения и его сложности [3]. При выборе подходящего набора шкал производительности необходимо сбалансировать их таким образом, чтобы учесть различные аспекты производственной эффективности [4,5]. Комплексное исследование основных показателей производительности должно учитывать не только традиционную перспективу, но и другие аспекты, такие как эффективность, результативность и рентабельность. Эффективность определяется как объемная разница между фактом и планом, результативность - факт относительно затрат, а определение рентабельности стандартно задается как дробь, в числителе которой общий доход, а в знаменателе затраты. В этом исследовании все четыре точки зрения называются продуктивностью управления и организации. Благодаря совершенствованию набора показателей эффективности управления и организации, двузначный Международный стандарт промышленной классификации (ISIC) по секторам будет проанализирован с помощью анализа охвата данных (DEA).

Методология определения эффективных

ПОКАЗАТЕЛЕЙ

На рис. 1 показана предлагаемый алгоритм определения наиболее эффективных показателей эффективности работы организации.

В табл. 1 представлены особенности предложенного алгоритма по сравнению с другими исследованиями. Из-за неопределенности и двусмысленности в мире бизнеса существует очевидная необходимость в использовании подходов, связанных с нечеткостью, для решения проблем, связанных с неопределенностью. Как показано в табл. 1, для решения проблем, связанных с неопределенностью, используются метод DEA, нечеткий метод DEA и статистические методы. Насколько известно, это первое исследование, в котором используется алгоритм оценки управленческих и организационных показателей с помощью количественных подходов. В предыдущих исследованиях данные и результаты не анализировались с помощью нечетких методов и не рассматривались какие-либо процедуры для уменьшения влияния возмущений. В исследовании также используется оценка возмущений и чувствительности для устранения возможного шума в данных и вычисления важности показателей.

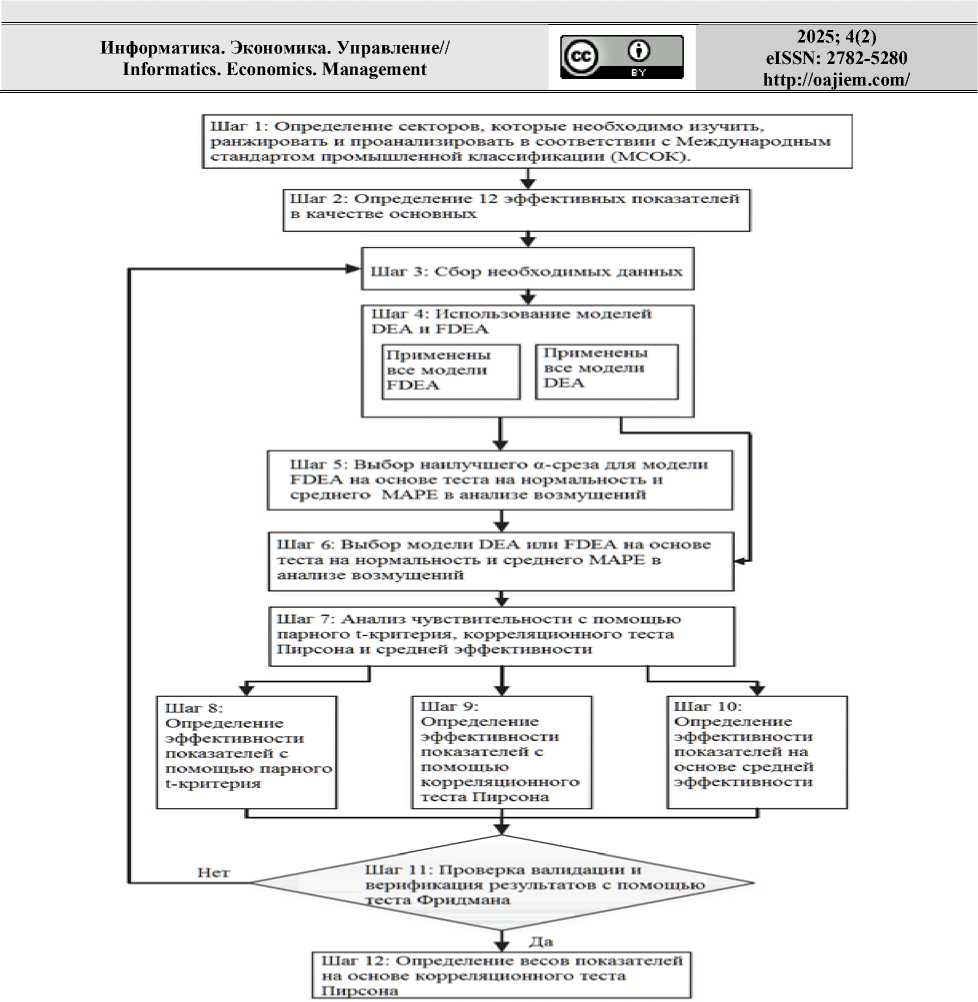
Рисунок 1. Структура алгоритма определения показателей. figure 1. Structure of the algorithm for determining indicators.

Анализ совокупности данных - это непараметрический метод, который определяет эффективность данного набора подразделений, принимающих решения (DMU), с помощью линейного программирования.

Эффективность фирм измеряется по шкале от 0 до 1 [6]. DEA является полезным методом для измерения производительности [7]. Он присваивает сравнительную эффективность каждому DMU и определяет каждый DMU как эффективный или неэффективный. Модели DEA можно разделить на категории с постоянной отдачей от масштаба (CRS) или переменной отдачей от масштаба (VRS), а также могут быть ориентированы на вход или выход. CCR и BCC -две основные модели DEA. Кроме того, DEA используется в различных областях.

Т аблица 1. О собенности показателей качества по сравнению с другими исследованиями .

TABLE 1. FEATURES OF QUALITY INDICATORS IN COMPARISON WITH OTHER STUDIES.

OJ S TO M О 4 OJ 4 О о s	s 4 и co Й о E OJ M о о E e	га OJ 4 & E E OJ 4	JS OJ E s о S О p н Е 3 & Е Е га м о Е к	о Е Рн Е JS Е Е О И О и со S Рн	о Рн S S Е Е О Q О Е Е S со Е Е га Рн о	Метод
						< Q	< Q N1 Э Рн	га Е *^ Е о Н ю о S о з s И 2 Рн 1) о М Е о ® Рн С	JS Е Е Q I 2 со М со Е Е <	S о о Е Е Ч W S м и Е со Е <
Настоящее исследование	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
[9]	✓	✓	-	-	-	-	-	-	-	-
[12]	✓	-	-	✓	-	-	-	-	-	-
[5]	-	-	-	✓	✓	-	-	-	-	-
[10]	✓	✓	✓	✓	✓	-	-	-	-	-
[14]	✓	✓	-	-	-	-	-	-	-	-
[23]	✓	✓	✓	-	✓	-	-	-	-	-
[24]	-	-	✓	✓	✓	-	-	-	-	-
[25]	✓	-	✓	-	✓	-	-	-	-	-

Неопределенность    является    основным источником неопределенности, который сложно рассчитать и которым сложно управлять. Классическая модель DEA не допускает неточных значений и считает все значения определенными. В то время как факт заключается в том, что все данные в реальном мире не являются точными, а являются неточными или двусмысленными. Это одна из самых важных трудностей классической модели DEA [8]. Для количественной    оценки    неточных    и расплывчатых данных полезным решением является нечеткая модель DEA. В последние годы все чаще используется теория нечетких множеств [9].

Непараметрический  анализ   данных

МЕТОДОМ DEA

Применяемая модель BCC, ориентированная на результат, аналогична модели (1). Согласно

модели (1), i - это индекс, который показывает входные данные (i=1), а r - это индекс, который показывает выходные данные (r = 1,2, . . ., 12), j -это индекс, показывающий DMU (j=1,2, . . ., 22). Также x i обозначает входные переменные, а y i -выходные.

Min θ;

xi0 ≥∑λjxij,i≥1 j=122

θyr0 ≤ ∑λjyrj,r = 1,

∑λj=1 λj=1j ≥ 0, j = 1,

...

,22

...,

Применяемая нечеткая модель проиллюстрирована следующим образом:

BCC

Max θ;

0(axm + (1 - a)xpp ) > ^[Ti(1 - a)xP]

22 j

aym + (1 - a)y0, < 2|\ (aym + (1 — а)у₽)], r = 1,...,12

j=1

Z j ¹

Tj> 0, Vj = 1,...,22

Модель     (2)     представляет     собой параметрическое линейное программирование. Эта модель может представить оптимальное решение для каждого заданного значения α, в то время как α принадлежит заданному интервалу. Также эффективность и ранг каждого DMU определяются на основе модели (2) для различных значений α.Параметр α в интервале [0, 39] представляет достоверность данных индикаторов. Когда α приближается к нулю, достоверность данных индикаторов снижается, что означает, что система становится более нечеткой. Напротив, когда α стремится к единице, нечеткая система переходит к определенной системе. Другими словами, повышается достоверность     заданных     показателей.

Компоненты модели (2) могут быть объяснены следующим образом:

i - входные данные; r - выходные данные; j - DMU;

• x ij^p - пессимистичное значение для входной переменной модели FDEA;

• x ij^m - наиболее вероятное значение для входной переменной модели FDEA;

• x ij^o - оптимистичное значение для входной переменной модели FDEA;

• y ij^p - пессимистичное значение для выходной переменной модели FDEA;

• y ij^m - наиболее вероятное значение для выходной переменной модели FDEA;

• y ij^o - оптимистичное значение для выходной переменной модели FDEA.

ЗАКЛЮЧЕНИЕ

Предлагаемый в статье алгоритм построения и моделирования    показателей    финансовой эффективности может быть легко использован в других производственных организациях с большим количеством площадок. Анализ охвата данных (DEA) применим для упорядочивания и анализа данных с помощью линейного программирования. Соответственно, DEA является эффективным методом, позволяющим выявлять слабые и сильные стороны и определять параметры производительности и улучшения, касающиеся состояния управления и организации в каждом секторе экономики.