Методика оценки страховых рисков на предприятиях нефтепереработки

С позиции оценки страховых рисков каждый потенциально опасный объект (ПОО) находится в различном страховом состоянии. В этой связи можно говорить о потоке страховых состояний, которые по своей сути являются последовательными. Будем утверждать, что поток страховых состояний отдельного объекта удовлетворяет условиям независимости, однородности и ординарности, т.е. представляет собой простейший поток [6].

Определим набор состояний для отдельного объекта страхования, наиболее выгодных для страхователя. Рассмотрим три основных состояния:

• •    первоочередное (приоритетное) страхование CPI (Condition Priority Insurance);

• •    обсуждаемое (второстепенное) страхование CSI (Condition Secondary Insurance);

• •    отсроченное (на некоторый период времени) страхование CDI (Condition Deferred Insurance).

Состояние CPI соответствует ситуации, при которой страхователю выгодно страховать определенный вид объектов, применительно к которым страховые выплаты в случае реализации страхового случая многократно покроют его расходы. В этой ситуации страховые риски r_s будут незначительными для страхователя ( r_s < 0,5).

Состояние CSI отражает то обстоятельство, что расходы страхователя могут быть значительными по сравнению с величинами страховых выплат при реализации страхового случая, а в лучшем случае могут только покрыть расходы страхователя. Тогда страховые риски r_s являются равновесными ( r_s = 0,5).

Состояние CDI определяет ситуацию, когда страхователю невыгодно страховать данный вид объектов, но делать это необходимо, поэтому процедуру по страхованию лучше отсрочить на некоторое время, когда у страхователя будет больше финансовых, экономических и иных возможностей. Страховые затраты при этом могут значительно превысить страховые выплаты в случае реализации страхового случая. Страховые риски r_s при этом будут значительными для страхователя ( r_s > 0,5).

Каждому из вышеописанных страховых состояний соответствуют следующие вероятности: CPI – вероятность V ₁( t ); CDI – вероятность V ₂( t ); CSI – вероятность V ₃( t ).

Выпуск 3/2020

Методы моделирования

Чтобы составить систему уравнений для динамики вероятностей V ₁( t ), V ₂( t ), V ₃( t ), определим интенсивности процессов β _ij ( i = 1, 2, 3; j =1, 2, 3), окончание которых означает переход из страхового состояния i в страховое состояние j . Тогда изменения указанных вероятностей описываются следующей системой дифференциальных уравнений Колмогорова [7] (рис.):

V1'(t ) = -₽bV, (t )+РзхV. (t),

V ‘ ( t ) = -p ₂ 3 V 2 ( t ) + Р з ₂ V 3 ( t ) ,                                     (1)

_ V ‘ ( t Mb V 1 ( t M23 V 2 ( t ) - ( в з1 +в з2 ) V з ( t ) .

Для разрешения этой системы заменим любое из ее уравнений (например, третье) условием нормировки V , ( t ) + V 2 ( t ) + V 3 ( t ) = 1. Тогда система уравнений (1) перепишется

Д                             [-Р,з V, (t )+Рз. Vз (t ) = К( t),

IL V2 (t ) + 032 V3 (t ) = V‘(t),                          (2)

_ V, (t) + V2 (t) + V3 (t ) = 1.

Выразим из третьего уравнения системы (2) функции V ₁( t ) и V ₂( t ):

V 3 ( t ) = 1 - V , ( t ) - V 2 ( t ) .                               (3)

Подставив соотношение (3) в систему (2), получим

/(—P13-P31) V, (t )-031 V2 (t )+031 = V,‘( t), \-P32 V, (t ) + (-023-P32) V2 (t ) + 032 = V^( t).

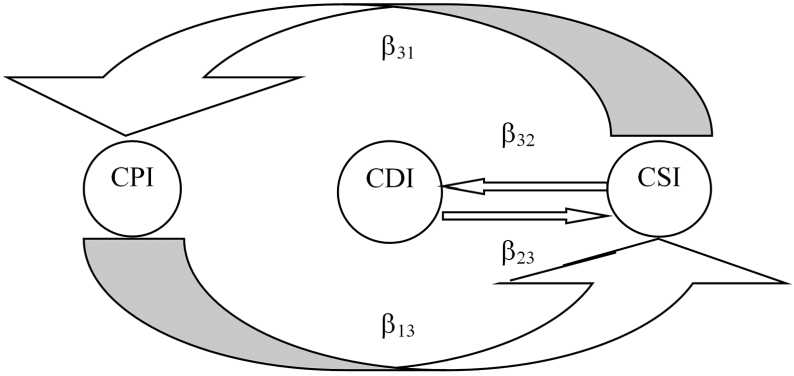
Схема взаимопереходов между страховыми состояниями

Вводя обозначения a ₁ = –β₁₃ – β₃₁; b ₁ = –β₃₁; a ₂ = –β₃₂; b ₂ = –β₂₃ – β₃₂, запишем следующую систему дифференциальных уравнений, где переменные со штрихами – производные по времени:

Грачев Д.С. Методика оценки страховых рисков на предприятиях...

^V 1 ⁽ t ) ~ a l ^V 1 ⁽ t ^{) + b}1 V 2 ⁽ t ^{) + в} 31 , _ ^V 2 ⁽ t ^{) =} a 2 V 1 ⁽ t ^{) + b} 2 ^V 2 ⁽ t ^{) + в} 32^.

Рассмотрим решение однородной системы:

/ V ' ( t ) = a V ( t ) + b l V 2 ( t ) , \ V^ t ) = a 2 V ( t ) + b 2 V 2 ( t ) .

Дифференцируя по времени первое уравнение из (6) и последовательно выполняя преобразования, найдем

V ‘ ( t ) = ( a ? + a 2 b 1 ) V ( t ) + ( a b + b b 2 ) V 2 ( t ) .                   (7)

Сформируем на основе первого уравнения (6) и соотношения (7) систему дифференциальных уравнений:

' V^ t ) = a 1 V ( t ) + b 1 V ₂ ( t ) ,

^V 1 ⁽ t ) = ( ^a 1 ⁺ a 2 ^b 1 ) ^V 1 ⁽ t ^{) + ( a}1^b1 ^{+ b} 1 ^b 2 ) ^V 2 ⁽ t ^{) .}

Выражая из первого уравнения (8) функцию V ₂( t ) и подставляя соотношение для нее во второе уравнение (8), придем к следующему дифференциальному уравнению второго порядка:

V1,,( t)-(a1+ b 2) V1,( t) + (a1b 2- a 2 b1) V1(t )=0.

Вводя обозначения K ₁ = –( a ₁ + b ₂); K ₀ = a ₁ b ₂ – a ₂ b ₁, запишем

V''( t) + K1 V'( t) + K 0 V1 (t ) = 0.(10)

Характеристическое уравнение для (10) имеет вид

X2 + к 1X+к 0 — 0,(11)

корни которого находятся из соотношения

_ ^a 1 + b 2

A

1,2         2

±

a² + b ² — 2 a 1 b ₂ + 4 a ₂ b 1

Чтобы выяснить, к полю каких чисел относятся корни уравнения (12) и каким образом записывается решение уравнения (1), необходимо численно оценить величины β _ij , отражающие переход из страхового состояния i в страховое состояние j .

С этой целью рассмотрим методику оценки β _ij , основанную на подходах теории активных систем [4]. Согласно моделям, предложенным в работе [3], ожидаемое значение целевой функции страхователя ObjF имеет вид

ObjF = RV - CT - PV - Ins + Ver x[(1+^)x Ind - Q ], (13)

где RV (Revenue) – доход от хозяйственной деятельности страхователя; CT (Cost) – его затраты на эту деятельность; PV (Preventive) – затраты на проведение предупредительных мероприятий против существующих опасностей; Ins (Insurance) – страховой взнос; Ind (Indemnity) – страховое возмещение; Ver – вероятность наступления страхового слу-

28 в ыпуск 3/2020

чая; ξ – коэффициент, отражающий отношение страхователя к риску; Q – потери при наступлении страхового случая.

В таком случае значение целевой функции страховщика Objf будем определять на основании следующего выражения [8]:

Objf = Ins — Ver X Ind.(14)

Страховой тариф при этом определяется как сумма нетто-ставки и нагрузки к нетто-ставке ξ (нагрузка к нетто-ставке включает рисковую надбавку, коммерческую надбавку и предупредительную надбавку), т.е.

Ins = ( Ver + ^0 )x Ind.(15)

При таком подходе условие выгодности страхования для страхователя имеет вид [Там же]

Ins < Ver x(1 + ^)x Ind,(16)

а для страховщика [Там же]

Ins > Ver X Ind.(17)

Условие морального риска (отражающее непобуждение страхователя к заинтересованности в наступлении страхового случая):

(1 + ^)x Ind < Q.(18)

Пусть имеет место полная компенсация ущерба, т.е. условие (18) выполняется как равенство. Тогда справедливы следующие соотношения [3]:

Ver + £

Ins =       0 ■ Q;(19)

1 + ^

Ind = -Q-.(20)

1 + ^

Из соотношений (19), (20) следует, что величина страхового взноса растет с увеличением вероятности наступления страхового случая, потерь и нагрузки к нетто-ставке. В то же время размер страхового возмещения растет с ростом потерь, убывает с ростом коэффициента ξ и не зависит от вероятности наступления страхового случая и нагрузки к нетто-ставке (что обусловлено введенным выше предположением о полной компенсации ущерба).

Подставляя выражения (19), (20) в целевые функции страхователя и страховщика и обозначая G = RV – CT – PV , получим

Objf = G - Vr^ ■ Q ;                  (21)

• ¹    + ^

E„

^ObjF = 1V₄ Q .                       (22)

Из (21)–(22) видно, что полезность для страхователя убывает с увеличением потерь, вероятности наступления страхового случая и нагрузки к нетто-ставке, а ожидаемая полезность страховщика не зависит от вероятности наступления страхового случая (объ-

Грачев Д.С. Методика оценки страховых рисков на предприятиях...

ясняется тем, что он не склонен к риску) и возрастает с увеличением потерь и нагрузки к нетто-ставке [3].

Выгодность для страховщика оценивается величиной ObjF , а выгодность страхования – величиной Objf .

В этом случае величины β _ij (где i = 1, 2, 3; j = 1, 2, 3) из уравнений (1) будем численно оценивать на основании следующих выражений:

'Р 13 = ObjF , в ³² = ObjF + Q , в ²³ = Ind + ObjF , в ³¹ = Objf ,

где переходные величины в левой части пока не выступают как интенсивности переходов в (1), являясь ненормированными и размерными величинами (поэтому отмечены верхними индексами).

Объясним смысл переходных величин β ^ij .

Первое. Переход страхования из приоритетного состояния CPI (выгодного для страхователя) во второстепенное состояние CSI вызван тем, что некоторый вид объектов требуется застраховать, но расходы на это могут значительно превышать величину страховых выплат или в лучшем случае только покрывать расходы страхователя при страховании данного объекта. То есть здесь более выгодны интересы страховщика, поэтому величина β13 определяется полезностью для него.

Второе. Переход в состояние CDI (отсроченное страхование) характеризует ситуацию, когда страхователю невыгодно страховать данный вид объектов, но делать это нужно в обязательном порядке; оценивается на основании величины β³², суммарно представляющей собой полезность для страховщика и те потери, которые понесет страхователь в случае реализации страхового случая по конкретному виду объектов.

Третье. Обратный переход из состояния CDI в CSI, отражаемый величиной β²³, определяется с учетом полезности для страховщика и страхового возмещения по конкретному виду объектов.

Четвертое. Величина β31, отражающая переход из состояния CSI в состояние CPI, определяется полезностью для страхователя.

Учитывая, что показатели в правой части (23) имеют размерность, перейдем к безразмерным интенсивностям β _ij , пронормировав величины β ^ij следующим образом:

ej =

в j

Ind + Q+Objf + 3 ObjF"

Пусть некоторый объект страхования описывается следующими финансово-экономическими показателями (табл. 1).

Таблица 1

Финансово-экономические показатели объекта страхования

Показатели объекта страхования
Ind	Q	Objf	ObjF

74 030

576,5606

878 945,8

113 908,2

30 в ыпуск 3/2020

Для рассматриваемого примера коэффициент β равен

ObjF                        113908,2

Pn =-------------------=---------------------------------------= 0,087941. (25)

• 13 Ind + Q + Objf + 3 ObjF 74030 + 576,5606 + 878945,8 + 3-113908,2

Остальные коэффициенты оцениваются как

P 32 =

ObjF + Q ---------^----------= 0,088386 ; Ind + Q + Objf + 3 ObjF

P₂₃=------ Ind ' OjF ------= 0,145095;

23    Ind + Q + Objf + 3ObjF

P₃₁ =---------- j --------= 0,678578

31    Ind + Q + Objf + 3ObjF

При таком определении нормированных β _ij , очевидно, выполняется условие

^P j =в 13 +P 32 +P 23 +P 31 = 1.

Значения корней характеристического уравнения λ1 = –0,13805; λ2 = –0,86195 относятся к полю действительных чисел, что соответствует общим решениям вида

W (t )=a1 e X1 t +a2 e x2 t.

Результаты и обсуждение

Численная оценка параметров βij применительно к реальному объекту произведена на основании информации о финансово-хозяйственной деятельности Рязанской нефтеперерабатывающей компании , являющейся одной из крупнейшей в России.

В таблице 2 приведены направления страхования НПЗ X_i ( i = 1, …, 8).

Таблица 2

Направления страхования

Номер направления	Название направления страхования
1	Объекты недвижимости
2	Производственное и технологическое оборудование
3	Товарно-сырьевые запасы, складское оборудование
4	Инвентарь, внутренняя отделка помещений, предметы интерьера, мебель, офисное и торговое оборудование
5	Денежная наличность, ценные бумаги, изделия из полу- и драгоценных материалов
6	Убытки от перерыва в хозяйственной деятельности
7	Потеря арендной платы
8	Расходы на расчистку территории

Величины целевых функций страхователя и страховщика рассчитаны для значения коэффициента ξ , отражающего отношение страхователя к риску, равного 0,5.

В таблице 3 приведены сведения о финансово-хозяйственной деятельности НПЗ «Рязанская нефтеперерабатывающая компания», необходимые для расчета численных значений по рассматриваемой методике для направлений страхования.

Грачев Д.С. Методика оценки страховых рисков на предприятиях...    31

Таблица 3

Значения величин, входящих в расчетные соотношения целевых функций страхователя и страховщика

	RV	CT	PV	Ins	Ind	Q	Objf	ObjF
X 1	23 613 503	21 436 915	1 215 035	177 500	74 030	576,5606	878 945,8	113 908,2
X 2	17 719 748	16 086 420	911 771,2	162 500	71 942	459,2634	628 321,5	116 126,2
X 3	5 393 445	4 896 301	277 520,2	96 000	17 684	58,16352	128 816,7	92 530,4
X 4	20 546 222	18 652 362	1 057 208	170 500	81 162,4	572,5819	756 717,9	109 837,6
X 5	2 078 758	1 887 147	106 962,7	60 000	10 764	21,8324	25 867,35	59 186,03
X 6	6 784 965	6 159 557	349 121	104 000	27 312	104,3141	182 373,1	97 258,85
X 7	7 422 722	6 738 528	381 936,8	112 000	29 708	115,264	202 258,4	103 978,2
X 8	1 611 436	1 462 901	82 916,58	50 000	6610	12,47153	16 198,95	49 612,52

На основании таблицы 3 по выражениям (24) рассчитаны значения параметров β _ij , входящих в систему дифференциальных уравнений (1), а также значения корней λ_1,2 характеристического уравнения (11) для направлений страхования (табл. 4).

Таблица 4

Переходные значения β ^ij и корни λ_1,2 характеристического уравнения

	X 1	X 2	X 3	X 4	X 5	X 6	X 7	X 8
β 13	113 908,2	116 126,2	92 530,4	109 837,6	59 186,03	97 258,85	103 978,2	49 612,52
β 32	114 484,8	116 585,5	92 588,56	110 410,2	59 207,86	97 363,17	104 093,5	49 624,99
β23	187 938,2	188 068,2	110 214,4	191 000	69 950,03	124 570,9	133 686,2	56 222,52
β31	878 945,8	628 321,5	128 816,7	756 717,9	25 867,35	182 373,1	202 258,4	16 198,95
λ1	–178 811	–175 827	–102 472	–179 759	–62 185,1	–114 443	–122 926	–51 122,2
λ 2	–1 116 467	–873 274	–321 679	–988 206	–15 2026	–387 123	–421 090	–120 537

Из таблицы 4 следует, что значения корней λ_1,2 характеристического уравнения (11) принадлежат полю действительных чисел, т.е. Х 1 2 G R , и не равны друг другу для каждого из направлений страхования. Как уже говорилось, в этом случае общие решения системы однородных уравнений типа (5) будут иметь вид (28) [1].

Частное решение системы (1) находится методом вариации произвольной постоянной [2]. (Чтобы не перегружать статью, процедура решения здесь не приводится.)

Найденное решение дало возможность численно оценить значения функций вероятностей V ₁( t ), V ₂( t ), V ₃( t ) через годовые промежутки времени для всех направлений страхования.

Важно: оценки показали, что изменение начальных условий не приводит к каким-либо изменениям значений функций вероятностей. В таком случае в поле страховых состояний устанавливается предельный стационарный режим, при котором осуществляются переходы из состояния в состояние, но вероятности состояний не меняются во времени. Поэтому имеет смысл говорить о предельном поведении вероятностей V_i ( t ) при t → ∞, т.е. о так называемых финальных вероятностях [5; 9].

32 в ыпуск 3/2020

В этой связи найдены финальные вероятности путем решения системы линейных алгебраических уравнений, полученных из дифференциальных уравнений Колмогорова:

• -R s V 1 + 0 31 V 3 = 0,

<-0 23 V 2 + 0 32 V 3 = 0,                              (29)

V + V 2 + V з = 1.

Определитель матрицы коэффициентов системы (29) отличен от нуля для любого βij, поэтому она имеет единственное решение:

V =

__________P 23 P 31__________

P 13 P 23 ⁺ 3 13 ^ 32 + ^в 23 ^в 31

V = 1 -в13 +Р31 V,

• ²             ₽ 31       1 ,

V 3 = 1 - V 1 - V 2 .

По соотношениям (30) найдены величины искомых вероятностей V ₁, V ₂, V ₃ для различных значений коэффициента ξ , отражающего отношение страхователя к риску. Показано, что значения финальных вероятностей не зависят от величины коэффициента ξ для всех направлений страхования, что дало возможность по значениям финальных вероятностей определить следующие приоритеты направлений страхования (табл. 5).

Таблица 5

Приоритеты направлений страхования

Номер направления	Название направления страхования
1	Объекты недвижимости
2	Инвентарь, внутренняя отделка помещений, предметы интерьера, мебель, офисное и торговое оборудование
3	Производственное и технологическое оборудование
4	Потеря арендной платы
5	Убытки от перерыва в хозяйственной деятельности
6	Товарно-сырьевые запасы, складское оборудование
7	Денежная наличность, ценные бумаги, изделия из полу- и драгоценных материалов
8	Расходы на расчистку территории

Заключение

• 1.    Для оценки страховых рисков применительно к потенциально опасным объектам целесообразно применять математическую модель в виде системы дифференциальных уравнений Колмогорова, описывающую набор возможных страховых состояний с переходами между ними в виде простейших потоков событий.

• 2.    В основе методики оценки величин, характеризующих переходы между страховыми состояниями, следует применять модели, основанные на описании процессов страхования, базируясь на подходах теории активных систем.

• 3.    Вероятностная модель оценки страховых рисков при использовании выражения для финальных вероятностей позволяет достаточно уверенно определять приоритеты на-

• Грачев Д.С. Методика оценки страховых рисков на предприятиях...   33

• 4.    Применительно к крупным предприятиям нефтепереработки приоритеты страхования (возможно, варьирующиеся в зависимости от особенностей конкретного предприятия) распределяются следующим образом: 1) объекты недвижимости; 2) инвентарь, внутренняя отделка помещений, предметы интерьера, мебель, офисное и торговое оборудование; 3) производственное и технологическое оборудование; 4) потеря арендной платы; 5) убытки от перерыва в хозяйственной деятельности; 6) товарно-сырьевые запасы, складское оборудование; 7) денежная наличность, ценные бумаги, изделия из полудрагоценных и драгоценных материалов; 8) расходы на расчистку территории.

правлений страхования, наиболее благоприятных для страхователя с финансово-экономической точки зрения.