Методика определения ортотропных свойств костного органа по данным компьютерной томографии

В настоящее время актуальной задачей выступает моделирование напряженно-деформированного состояния пористых многофазных сред, одной из которых является костная ткань. При моделировании поведения костной ткани [9, 25, 26, 30, 33] необходимо учитывать анизотропные свойства среды, определяемые особенностями различных видов костных органов в зависимости от их функционала, возраста, пола, среды обитания и т.п.; таким образом, данная задача остаётся актуальной. В случае моделирования адаптационных процессов [10–13, 20, 34], возникающих в костной ткани под воздействием внешних силовых воздействий, необходимо знать начальное

Харин Никита Вячеславович, лаборант-исследователь кафедры теоретической механики, Казань Герасимов Олег Владимирович, лаборант-исследователь кафедры теоретической механики, Казань Большаков Павел Владиславович, лаборант-исследователь кафедры теоретической механики, Казань Хабибуллин Азат Айдарович, аспирант кафедры теоретической механики, Казань

Балтин Максим Эдуардович, аспирант кафедры физиологии человека и животных, Казань Балтина Татьяна Валерьевна, к.б.н., доцент кафедры физиологии человека и животных, Казань Саченков Оскар Александрович, к.ф.-м.н., научный сотрудник кафедры теоретической механики, Казань состояние костного органа, а значит, распределение в теле анизотропных свойств. Для определения механических свойств пористого материала необходимо проведение натурных экспериментов, но данный метод является дорогостоящим и требует большого количества однотипных образцов; более того, его использование невозможно без разрушения самого костного органа.

На сегодняшний день развитие компьютерной томографии позволяет получать информацию о структуре образца без разрушения, а распространённость компьютерных томографов в клинике расширяет область применения методики в задачах биомеханики. Развитие мощностей компьютерных томографов расширяет область применения метода на микроуровне (микробиология, кристаллография и т.п.) и макроуровне (медицина, машиностроение, нефтяная промышленность и т.п.). Вкупе с современными численными методами это позволяет решать задачи для структурно сложных систем и проводить численные эксперименты.

Целью данной работы является создание методики анализа распределения ортотропных свойств костного органа по данным компьютерной томографии.

Материалы и методы

Компьютерная томография образца представляет собой цифровой прототип исследуемого объекта, где каждое число суть нормированный по шкале Хаунсфилда коэффициент рентгеновского ослабления. Определяя порог бинаризации, можно дифференцировать материал и воздух (поры). В полученном бинаризированном массиве представляется возможным определение замыкающих поверхностей, которые формируют объем объекта. При предлагаемом подходе предлагается дискретизировать исследуемый объем на репрезентативные элементы, для каждого из которых в последующем необходимо определить механические свойства в численных экспериментах. Получаемый набор механических констант для репрезентативных объемов подвергается статистическому анализу с целью восстановления аппроксимирующих функций.

Из предположения, что анизотропия костной ткани определяется неравномерностью распределения пор по объему [15, 22, 32], в расчетах можно предположить, что сам материал костной ткани изотропен. В дальнейшем применяется метод представительных объемов, нашедший распространение в механике композиционных материалов и достаточно разработанный в настоящее время [1–6, 19, 27, 35]. Кроме того, он на основе данных компьютерной томографии применяется в геологии и биомеханике [28]. Существуют оценки адекватности получаемых результатов в сравнении с другими методами [16, 21, 29, 36] и для различных моделей компьютерных томографов [14]. Определить напряженно-деформированное состояние исследуемого объема можно с помощью метода граничных элементов [17] и метода конечных элементов [18, 24, 31, 36]. Последний используется в данной работе.

В каждом представительном элементе можно построить регулярную конечноэлементную сетку по данным томографии: в этом случае физический размер элемента соответствует размеру вокселя томографии. Полученная конечно-элементная сетка трансформируется согласно бинаризированным данным компьютерной томографии. Для определения порога бинаризации в работе был использован метод Отцу. Затем для полученного конечно-элементного ансамбля проводятся численные эксперименты: три на осевое сжатие и три на чистый сдвиг (рис. 1).

После решения задачи напряженно-деформированного состояния компоненты напряжения усредняются:

• - d dA = C • £ 0 , jj

  
  

AA где σ – вектор напряжений; ε – вектор деформаций; j – индекс в нотации Фойгта.

Таким образом, в результате численных экспериментов можно получить 36 линейных уравнений, в то время как неизвестных – 21. Для решения переопределенной системы применяется метод наименьших квадратов.

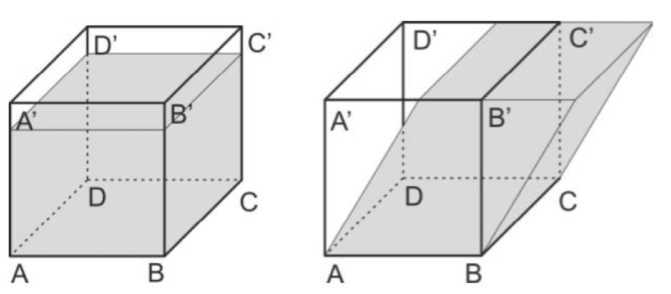
а                               б

Рис. 1. Схема нагружения в численных экспериментах: а – одноосное сжатие; б – сдвиг

На следующем шаге необходимо определить оси ортотропии и величины механических характеристик, для чего компоненты тензора упругих констант выписываются относительно трех углов поворота [7], по которым минимизируется целевая функция:

36       63        6

2 ZH C * ) ’ + 2 ZH C ) + 4 Z ( C ) ²

f =

• i = 1 j = 4 __________________ i = 4 j = 1 _________________ i , j = 4, j * i ___________

  
  

Z( Cj)2 + 4 Z( Cjt i, j=1                   i, j=4

Подробно методика описана в работе [8]. В результате расчетов для каждого репрезентативного элемента можно определить оси ортотропии и механические характеристики в этих осях. Полученные результаты представляют собой тензорное поле над объемом объекта. Для практических расчетов удобно использовать аппроксимации полученных механических свойств.

Результаты и обсуждение

Приведенная методика была реализована для определения характеристик диафиза бедренной кости крысы. Сканирование образца выполнено с применением микро-/нанофокусной системы рентгеновского контроля для компьютерной томографии и 2D-инспекции Phoenix V|tome|X S240 в лаборатории рентгеновской компьютерной томографии Института геологии и нефтегазовых технологий Казанского (Приволжского) федерального университета. Система оснащёна двумя рентгеновским трубками: микрофокусной с максимальным ускоряющим напряжением 240 кВ, мощностью 320 Вт и нанофокусной с максимальным ускоряющим напряжением 180 кВ, мощностью 15 Вт. Для первичной обработки данных и создания объёмной (воксельной) модели образца на базе рентгеновских снимков (проекций) используется программное обеспечение datos|x reconstruction. Зафиксированный в держателе образец помещается на вращающийся столик камеры рентгеновского компьютерного томографа на оптимальном расстоянии от источника рентгеновского излучения. Для полученных образцов была использована нанофокусная трубка. Съёмка проводилась при ускоряющем напряжении 90–100 кВ и токе 140–150 мА.

Диафиз был разделен в поперечном сечении на 10 репрезентативных элементов и на 22 репрезентативных элемента в продольном направлении (всего 220 репрезентативных элементов). На рис. 2, а приведены данные томографии, на рис. 2, б – разбиение на репрезентативные элементы. Каждый репрезентативный элемент представляет собой куб с размером 42×42×42 вокселя, размер вокселя – 9,73 мкм.

Материал костной ткани задавался следующими характеристиками: модуль Юнга, равный 20 ГПа, и коэффициент Пуассона, равный 0,3 [23, 32]. После задания свойств материала проводились численные эксперименты по описанной методике [8]: определялись оси ортотропии и константы тензора упругости. На рис. 2, в представлены полученные направления осей ортотропии: для наглядности срединная поверхность образца аппроксимирована полигонами. Одно направление ортотропии совпадало с продольным направлением, два других располагались в поперечной плоскости.

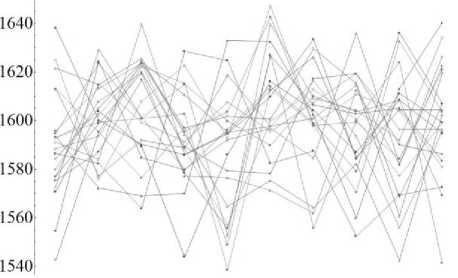
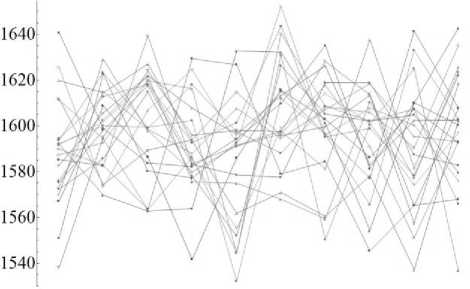
Для анализа характера распределения упругих констант в пространстве весь набор данных был сгруппирован по продольным и поперечным направлениям. После этого в каждой из групп оценивалось распределение механических характеристик. Для обеих групп было получено нормальное распределение, а значит, для описания состоятельны средняя величина и стандартное отклонение. При анализе модуля Юнга по оси Х в поперечном направлении (рис. 3, а ) величина составила 1590,42 ± 6,29 МПа (0,39%), в продольном (см. рис. 3, б ) – 1597,37 ± 6,62 МПа (0,41%). При анализе модуля Юнга по оси Y в поперечном направлении (см. рис. 3, в ) – 1595,8 ± 6,68 МПа (0,41%), в продольном (см. рис. 3, г ) – 1595,8 ± 6,93 МПа (0,43%). При анализе модуля Юнга по оси Z в поперечном направлении (см. рис. 3, д ) величина составила 12254,3 ± 34,16 МПа (0,27%), в продольном (см. рис. 3, е ) – 12254,3 ± 19,34 МПа (0,15%).

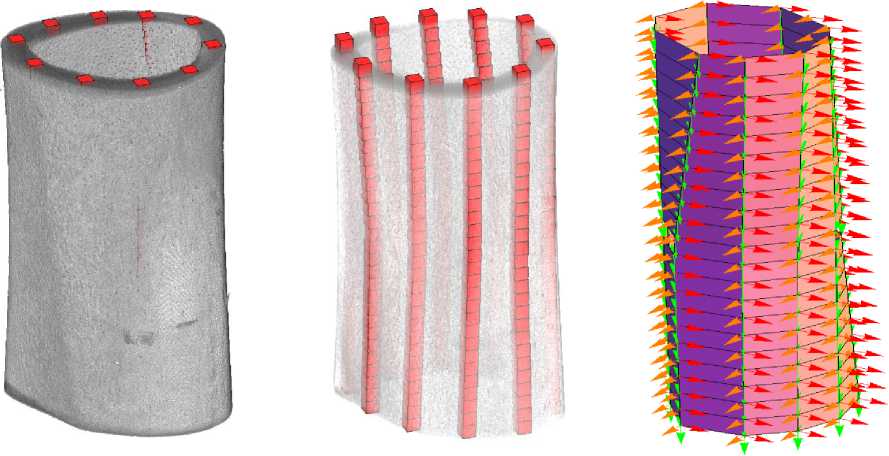
а                               б                              в

Рис. 2. Компьютерная томография костного органа ( а ), дискретизация на репрезентативные элементы ( б ) и полученные направления ортотропии ( в )

а

в

б

д

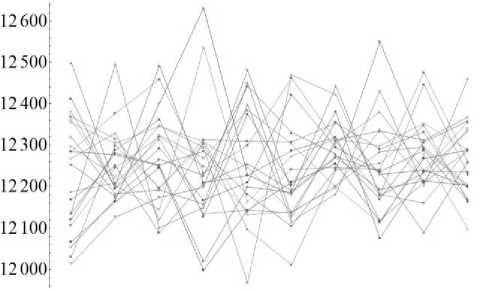
е

Рис. 3. Распределение средних значений модуля Юнга, МПа, по слоям в определенных направлениях: а – по оси Х в продольном направлении; б – по оси Х в продольном направлении; в – по оси Y в продольном направлении; г – по оси Y в поперечном направлении; д – по оси Z в продольном направлении;

е – по оси Z в поперечном направлении

Сравнивая среднее значение модулей Юнга по всем слоям в направлениях X и Y , получаем, что абсолютная разница между ними не превышает 0,098%, а значит, можно заключить, что образец обладает трансверсальной изотропией. Аналогично проделав описанные операции для модуля сдвига и коэффициента Пуассона, можно показать, что упругие константы не зависят от пространственной координаты. В результате расчетов было получено, что отклонение от среднего не превышает 0,33%. Таким образом, модуль сдвига в плоскости XY составил 24640 ± 41 МПа, а в двух других направлениях – 1726 ± 3 МПа. Осредненные значения упругих констант приведены в таблице.

Осредненные значения упругих констант

Упругая константа	Индекс компоненты
	11	22	33	12	23	13
E , МПа	1590	1590	12 205	—
G , МПа	—			24542	1718	1718
ν				0,87	0,021	0,021

Для наглядности на рис. 4 приведены поверхность тензора упругих констант и ее сечения плоскостями.

а

б

в                                                    г

Рис. 4. Тензорная поверхность ( а ) и ее сечения: б – в плоскости XY ; в – в плоскости YZ ; г – в плоскости XZ

Заключение

• 1.    В работе представлена методика для определения распределения упругих констант образца по данным томографии. В используемой методике изучаемый объект предлагается разбить на набор репрезентативных объемов, на основе данных томографии для каждого объема производится построение конечно-элементной модели

• 2.    В работе рассмотрен диафиз бедренной кости крысы, для описания которого использована данная методика. В результате расчетов было показано, что образец обладает трансверсальной изотропией, не зависящей от пространственной координаты; были определены средние величины упругих констант и их стандартные отклонения.

• 3.    Результаты, полученные при применении описанной методики, могут быть улучшены путем увеличения количества численных экспериментов и регуляризаций задачи определения компонент тензора упругих констант.

• 4.    Описанный подход может быть расширен не только на объекты из костной ткани, но в этом случае необходима некоторая априорная информация о структурных составляющих.

и проводятся численные эксперименты. В результате можно получить распределение упругих констант в объекте. В дальнейшем для оценки получаемого распределения предлагается использовать методы статистического анализа.

Благодарности

Работа выполнена при финансовой поддержке Российского научного фонда, проект № 18-75-10027.