Методика построения диагностики состояния оптико-электронных систем

В настоящее время оптико-электронные системы (ОЭС) решают широкий круг практически важных задач, таких как определение формы, размеров, позиции и ориентации наблюдаемых объектов сцены. Однако для реализации всего потенциала ОЭС на практике большое значение имеет техническое состояние ОЭС в каждый момент времени и точное позиционирование наблюдаемого объекта по отношению к оптической оси ОЭС. Неточное позиционирование объекта относительно оси оптической системы на аппаратном уровне изменяет линейное увеличение объекта в плоскости регистрации и размывает структуру его изображения, тем самым изменяет условия проведения обработки полученной информации. Принято считать, что для получения достоверных результатов средствами ОЭС сфокусированного изображения необходимо согласовывать параметры оптической системы, обеспечивающие глубину резко отображаемого пространства (ГРОП), с разрешающей способностью приемника изображения. В простейшем случае полагается, что точность функционирования ОЭС при сфокусированной на объект ее оптической системы будет равна шагу дискрет-

ности структуры элементов сенсора изображения, или размеру светочувствительных элементов матричного фотоприемника. Дополнительные системы, обеспечивающие точную фокусировку в процессе эксплуатации, усложняют ОЭС, при этом не решают проблемы резкости изображения при отображении объемно-протяженных объектов (различные части изображения могут иметь различную плоскость фокусировки). В процессе эксплуатации ОЭС могут изменяться как конструктивно заданные параметры оптической системы, так и позиционирование наблюдаемых объектов, что требует проведения ее постоянной диагностики и юстировки. Как правило, диагностика ОЭС является самостоятельной и трудоемкой операцией, проводимой в специальных условиях. Поэтому диагностика состояния ОЭС в процессе ее эксплуатации является актуальной задачей, которая в настоящее время в полном объеме не решена. Ее реализация повысит производительность, обеспечивая надежность получаемых результатов.

Обзор

Как правило, анализ состояния ОЭС базируется на критериях качества получаемого изображения, которое определяет достоверность отображения отдельных элементов наблюдаемых объектов. Основным признаком достоверности работы ОЭС является сохранение формы и масштаба как частей наблюдаемых объектов, так и всего объекта, отображение цветов или градаций оттенков (при заданных условиях освещения). Немаловажным вопросом состояния ОЭС является также степень размытия контраста элементов изображения. Мерой качества реальной оптической системы (ОС) является степень ее отклонения от идеальной системы [1]. Свойства ОС приводят в первую очередь к изменению геометрического подобия отображения в отдельных частях наблюдаемого объекта. Во вторую очередь в реальных ОС нарушается второй принцип идеальной системы – каждой отображаемой точке объекта не соответствует единственная точка в его изображении, что обусловливает размытие изображения и увеличивает неопределенность в получении той или иной доминантной составляющей (интересующего параметра), например координат при детектировании контрастных границ фрагментов изображения. В отличие от алгоритмов непосредственного детектирования границ изображения по уровню распределения освещенности на базе алгоритмов компарирования и дифференцирования [2], более сложные алгоритмы, такие как, например, непрерывное вейвлет-преобразование (НВП) [3], позволяют с большей точностью детектировать и определять координаты границ фрагментов изображения, в том числе в расфокусированной ОС [4]. Это говорит о том, что при ухудшении качества получаемого ОС-изображения не всегда теряется большая часть его информационных составляющих. В то же время получаемое ОС-изображение содержит информацию о факторах, вызывающих его искажение.

Для точного определения характеристик элементов изображения и его контрастных границ можно использовать различные алгоритмы, такие как фильтрация [5], двухмерное разложение по различным базисным функциям [6; 7], методы вейвлет-анализа [8–10]. Известно, что амплитуда и ширина всплесков кривой коэффициентов НВП [3] определенным образом зависят от контраста и размытия границы изображения. Таким образом, на уровне обработки полученного в ОЭС изображения методом НВП имеется больше возможностей параллельно выявлять различные дефекты в работе самой ОС [4], в том числе определять такие параметры, как механическая стабильность регистрируемого объекта относительно ОЭС [11].

Можно видеть [11], что анализ результатов НВП-распределения освещенности в изображении позволяет определять первую и вторую производные распределения освещенности в области размытия градиента контраста (границ) изображения (аберрацию, расфокусировку, механическую нестабильность ОС и приемника изображения), а также локальный контраст освещенности в изображении. Далее, в конкретной оптической системе размытие границ изображения позволяет определить величину

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

расфокусировки оптической системы, что дает возможность реализовать последующую корректировку полученных результатов анализа и измерения параметров изображения [12].

В методах идентификации границы изображения, основанных на методе компари-рования уровня освещенности [3], размытие границ изображения (расфокусировка) в первую очередь снижает потенциальную точность определения координат границ отдельных фрагментов (так как координаты зависят от уровня освещенности и выбора оптимального порога компарирования) [12]. Определение границы изображения методом дифференцирования и НВП-распределения освещенности позволяет получить некоторую целевую функцию с резко выраженными особенностями поведения в зоне границ изображения (изменения контраста) - всплесками [3]. В этом случае процесс анализа изображения сводится к определению координат выявленных особенностей поведения целевой функции (всплесков) и практически не зависит от параметров самого алгоритма обработки. Основная проблема заключается в том, что при наличии шума процедура дифференцирования для малой выборки сигнала дает значительную погрешность определения целевой функции.

Моделирование распределения освещенности идеального изображения различного контраста с заданным размытием границ подтверждает тот факт, что амплитуда всплесков кривой коэффициентов НВП в зоне изменения контраста изображения линейно уменьшается в зависимости от контраста и размытия границ в изображении [3]. При этом ширина всплесков кривой коэффициентов НВП практически не зависит от контраста и линейно возрастает с размытием границ. Коэффициенты пропорциональной зависимости амплитуды и ширины всплесков НВП от размытия контраста определяются исключительно типом используемого вейвлета, т. е. его фильтрующими свойствами (Фурье-образом). При этом для распределения освещенности для идеального теневого изображения с размытыми определенным образом границами методом НВП можно с более высокой точностью определять расстояние между противоположными границами структурного элемента изображения (линейный размер). При этом предполагается, что сохраняется характер градиента изменения освещенности.

Из приведенного обзора можно видеть, что целый ряд алгоритмов анализа изображений содержит информацию не только о регистрируемом объекте, но и о состоянии ОЭС. Данная информация может быть определена путем анализа коэффициентов разложения изображения по некоторому базису. Все это создает предпосылки проводить анализ состояния ОЭС в процессе регистрации тестовых или реальных объектов. При этом встает вопрос разработки общей методики применения различных алгоритмов для диагностики состояния ОЭС, интерпретации результатов анализа, их достоверности и точности, определения условий проведения такой диагностики: требование к регистрируемому объекту, условиям освещения и т. д. Как следует из приведенного обзора, ранее эти вопросы в полной мере не рассматривались. Разработка такой методики позволит повысить надежность результатов анализа наблюдаемых объектов, получаемых при помощи ОЭС.

Цель работы

Выявление основных факторов, приводящих к ухудшению качества изображения в оптической системе, разработка принципов и методики диагностики ОЭС по оптическому изображению, интерпретации ее результатов, определение достоверности и точности результатов диагностики.

Материал исследования

Получение изображений в реальных оптических схемах ОЭС всегда связано с целым рядом специфических дефектов, таких как дифракция, дисторсия, разъюстиров-ка ОС, ориентация объекта по отношению к углу визирования ОС, неравномерность освещенности, дефекты сенсора изображения и т. д. Поэтому для оценки таких ОЭС необходимо провести теоретические и экспериментальные исследования их работы в широком диапазоне изменения ее параметров и воздействующих факторов.

Исследования проводились путем проведения измерений линейных размеров структурных элементов объектов в модельных и реальных изображениях с использованием цифровых камер (ЦК) различного принципа действия [4; 12]. Учитывая различные принципы действия сенсоров изображения [13], целесообразно на первом этапе проведения исследований выбрать цифровую камеру с простым сенсором изображения – ПЗС без массива цветных фильтров. В качестве ЦК ОЭС для исследований в работе использована смарт-камера NI 1722, которая имеет монохромную ПЗС-матрицу Sony ICX424AL с форматом 1/3 дюйма, 640×480 пикс.

В экспериментальных исследованиях заведомо задавалась совокупность достаточно неблагоприятных условий получения изображения регистрируемого объекта: дисторсия, неравномерность и неоднородность освещения по полю, разъюстировка оптической системы (несоосность объектива приемнику ПЗС), развороты объекта относительно оптической оси объектива ОЭС, локальные дефекты в пло скости сенсора.

Для одинаковой группы всех ухудшающих изображение факторов были использованы результаты ранее проведенных экспериментальных исследований процесса измерения линейных размеров между заданными элементами наблюдаемого объекта в зависимости от контраста и величины расфокусировки оптической системы [12; 14]. В качестве объекта исследования использовалась щель монохроматора. Изменяя ее ширину, можно моделировать заданный геометрический размер. Оптическая схема (объектив) настраивалась таким образом, чтобы путем линейного увеличения получать максимально установленный размер щели в 3/4 размера приемной матрицы ПЗС-камеры.

Для одинаковой группы всех ухудшающих изображение факторов были проведены экспериментальные исследования процесса контроля геометрических параметров тестового объекта (щель монохроматора) в зависимости от контраста и величины расфокусировки оптической системы [14]. Общий контраст изображения задавался программно путем изменения времени экспозиции на смарт-камере ( E ) в диапазоне от 2 до 10 с шагом 1 (при заданном коэффициенте усиления G = 321, заданном напряжении питания осветителя). Величина расфокусировки оптической системы задавалась перемещением тестовой щели и осветителя вдоль оптической оси в пределах Δ z = –0,32 – 0 – +0,32 мм с шагом 10 мкм (65 точек). Предельно расфокусированные и сфокусированное теневые изображения щели при максимальном контрасте показаны на рис. 1.

а)                                    б)                                    в)

Рис. 1 . Изображения щели при различной величине расфокусировки оптической схемы и различном контрасте:

а) E = 10, Δ z = –0,32; б) E = 10, Δ z = 0; в) E = 10, Δ z = 0,32

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Для проведения измерений использовался виртуальный прибор (ВП), созданный в приложении NI Vision Assistant 2009 [14]. Для измерения линейного размера ширины по изображению щели использовался исследовательский ВП, реализующий различные алгоритмы обработки полученного изображения: стандартный алгоритм измерения (нахождение лучших прямых, проходящих через границы изображения) из пакета технического зрения IMAQ Vision (Adv.Straigh Edge); алгоритм на базе дифференцирования интегрального на заданной высоте ( c ) распределения освещенности теневого изображения; алгоритм на базе непрерывного вейвлет-преобразования (НВП) интегрального на заданной высоте ( c ) распределения освещенности теневого изображения. Исследовательский ВП позволял параллельно проводить анализ функций коэффициентов НВП: координату максимума, амплитуду и ширину контура всплеска в зоне границ изображения.

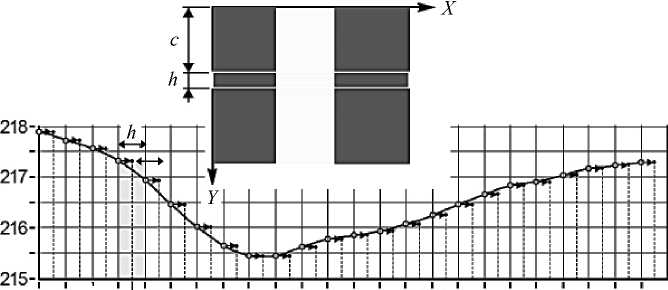
Предварительный анализ параметров ОС относительно объекта контроля проводился путем измерения ширины щели ( b ) стандартным алгоритмом измерения (Adv. Straight Edge), который, как известно, позволяет получать хорошие результаты измерения для сфокусированного изображения при достаточно высоком уровне контраста. Результат измерений линейных размеров представлялся в виде массива значений для каждой прямоугольной зоны ( h ) на заданной высоте ( c ) изображения щели (рис. 2).

о c J 100              200              300              400

Рис. 2. Зависимость измерений ширины щели ( b ) по высоте в зависимости от освещенности и смещения вдоль оси f ( c , E , Δ z ) ( E = 10, Δ z = 28 точек)

Из результатов измерений ширины щели, полученных стандартным алгоритмом, видно, что оптическая система, имеющая линейное увеличение β _os = 4,93, имеет ярко выраженную подушкообразную дисторсию. Несоосность объекта контроля оптической системе приводит к несимметричному и смещенному контуру распределения результатов измерений по высоте. Минимальный размер ( d _min = 215,47 пикс) лежит выше центра ( c _min = 190 пикс). При этом максимально измеренный размер по высоте d _max = 217,90 пикс ( c _max = 10 пикс), средний размер – d_av = 216,57 пикс. Таким образом, гарантированная точность измерения стандартным алгоритмом при заданных разворотах объекта контроля относительно оптической оси будет составлять δ d ≈ ±1 пикс.

Далее для данной оптической системы проводились исследования зависимости параметров всплесков кривой коэффициентов НВП (для вейвлета типа bior 3_1) в зоне границ его изображения для широкого диапазона расфокусировки оптической схемы и контраста изображений в плоскости сенсора. Исследовались такие параметры кривой коэффициентов НВП, как максимальная амплитуда и ширина всплеска для правой и левой границы изображения щели. Для простоты определения амплитуды и шири- ны всплесков коэффициентов кривой НВП оценка производилась по аппроксимирующему ее Гауссиану:

( x[i] -ц । y [ i ] = a exp I      5 I + b,                                    (1)

V 20 V где a – амплитуда; σ – среднеквадратичное отклонение (ширина).

Из графиков зависимости σ( E , c ) видно, что координаты минимума ширины кривой коэффициентов НВП определяются максимальной видимой резкостью соответствующих границ щели ( c _min1 = 0,01 мм, c _min2 = –0,025 мм). Положения плоскостей резкого изображения для правой и левой границ не совпадают (имеется разворот щели относительно оптической системы). В то же время ширина всплесков кривой σ( c , E ) коэффициентов НВП при различной величине расфокусировки для каждой границы практически не зависит от контраста изображения. Погрешность определения величины расфокусировки оптической системы δ с по ширине всплеска коэффициентов НВП в широком диапазоне контраста составляет величину ~ ±0,005–0,01 мм. При этом в зоне сфокусированного изображения (практически в диапазоне ГРИП) точность определения расфокусировки будет достаточно низкой. Однако, в отличие от идеально размытых границ теневого изображения, кривые для левой и правой границ изображений не совпадают по размаху для одинаковой величины расфокусировки оптической системы, что определяется влиянием всех видов разъюстировок оптической системы и ее аберрациями. В то же время для определенной конфигурации оптической системы по отношению к объекту контроля коэффициенты НВП (CWT-коэффициенты) позволяют достаточно точно определить текущее значение расфокусировки изображения каждой границы независимо от контраста изображения.

При дефекте неравномерной фокусировки по полю (правый край изображения) нарушается симметрия внутри контура распределения CWT-коэффициентов (рис. 3).

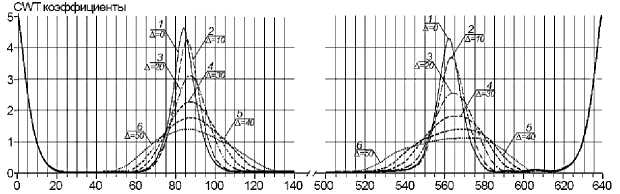
Рис. 3. Графики коэффициентов НВП левой и правой границ изображения в зависимости от величины расфокусировки оптической системы

При падении освещенности амплитуда коэффициентов НВП становится меньше, а форма кривой – более пологой (рис. 4).

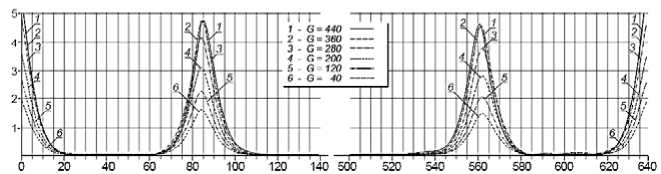
Рис. 4. Зависимость коэффициентов НВП от уровня освещенности для сфокусированного изображения

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Расфокусировка изображения и аберрации приводят к изменению формы кривой и смещению максимумов коэффициентов НВП (рис. 5). Однако центр тяжести кривых коэффициентов НВП менее чувствителен к величине расфокусировки изображения.

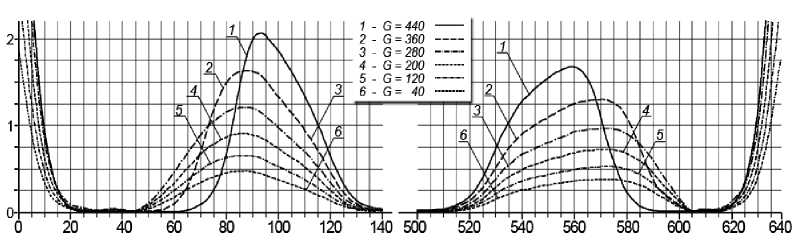
Рис. 5. Зависимость коэффициентов НВП от уровня освещенности для расфокусированного изображения

Зависимости амплитуды всплеска a ( E , c ) кривых коэффициентов НВП интегрального распределения освещенности по всей высоте в том же теневом изображении щели в зоне левой (1) и правой (2) ее границ от величины расфокусировки и контраста изображения представлены на рис. 4 и рис. 5 соответственно.

Максимальные значения амплитуд всплеска кривых коэффициентов НВП практически линейно зависят от контраста изображения, а ее экстремумы в сечении контраста почти точно соответствуют максимальной видимой резкости соответствующих границ изображения. При расфокусировке оптической системы амплитуды всплесков коэффициентов НВП плавно уменьшаются. Из графиков видно, что в некоторых местах поверхности имеются аномальные отклонения формы поверхности (выпадение результатов измерения из плавной зависимости). Данные выпадения результатов вызваны в большей степени некорректностью определения амплитуд всплесков коэффициентов НВП по аппроксимирующему Гауссиану.

Таким образом, анализ основных параметров всплесков кривой коэффициентов НВП, полученных на границах теневого изображения, позволяет достаточно точно определить основные параметры состояния сложной оптической осветительной и измерительной систем по отношению к объекту контроля в момент проведения измерения, таких как расфокусировка, контраст теневого изображения.

Выводы

Измерение линейных размеров в тестовых изображениях алгоритмами нахождения координат границ позволяет определить параметры дисторсии и несоосности для заданного положения и углов визирования.

Экспериментальные исследования показали, что метод непрерывного вейвлет-преобразования позволяет проводить детальный анализ основных параметров состояния оптической системы (расфокусировка, контраст).

Анализ всплесков кривой коэффициентов НВП дает возможность определить степень разъюстировки оптической системы, ориентацию объекта контроля, расфокусировку, равномерность освещенности (степень контраста левой и правой границ изображения). Это позволяет проводить как предварительный анализ оптической системы, так и ее мониторинг в процессе эксплуатации.