Методика прогнозирования динамических характеристик и испытательных режимов, реализуемых виброударными стендами взрывного действия

Одним из факторов, определяющих надёжность бортовой аппаратуры ракет и космических аппаратов, является устойчивость функционирования в условиях воздействия интенсивных широкополосных виброударных нагрузок от срабатывания пиротехнических средств разделения, широко используемых на практике. Уровень нестационарных ускорений, воздействующих на аппаратуру, изменяется в диапазоне 30…10 000 g, в частотной полосе 0,1…10,0 кГц [1, 2]. Автономные испытания бортовой аппаратуры ракет и космических аппаратов на воздействие виброударных нагрузок от срабатывания пиротехнических средств разделения регламентированы рядом нормативных документов. В частности, в рамках программы унификации отечественных стандартов выпущен стандарт [3], согласно которому внешние широкополосные вибрационные нагрузки нормируются по ударному спектру [4]. Выпускаемые серийно вибростенды не могут обеспечить реализацию виброударных нагрузок во всём указанном диапазоне ускорений и частот. Для проведения таких испытаний в АО «ЦНИИмаш» были разработаны и в течение многих лет используются виброударные стенды взрывного действия [5, 6]. Основу стендов этого типа составляет система упруго-инерционных элементов, образующих многочастотный резонатор, возбуждаемый при срабатывании взрывного источника энергии. Возникающие в резонаторе нестационарные вибрации передаются соединённому с ним объекту испытаний. Одна из основных проблем, возникающих при использовании виброударных стендов взрывного типа, состоит в необходимости проведения большого объёма отладочных испытаний, в процессе которых на габаритномассовых макетах отрабатываются требуемые режимы испытаний, заданные в форме ударного спектра. В процессе отладочных испытаний подбираются динамические характеристики сменных конструктивных элементов стенда и параметры взрывной нагрузки. Как правило, объём отладочных испытаний близок, а иногда и превышает объём собственно испытаний. Одним из способов повышения качества и снижения трудоёмкости испытаний является использование предыспытательного математического моделирования. Для этого прежде всего необходимы динамические модели стенда, позволяющие проводить компьютерный анализ будущих испытаний, сокращающий этап отладки режимов. В настоящей статье излагаются методические основы синтеза динамических характеристик виброударных стендов и приводятся динамические модели для типовой схемы стенда, используемой в линейке испытательных устройств, разработанных и применяемых в практике Центра прочности АО «ЦНИИмаш». Основу стендов составляют упругие пластины и кольца в различных сочетаниях: одноярусная или двухъярусная компоновка (рис. 1).

Базовая схема резонатора вибро-ударного стенда представляет собой систему плит (балок), опёртых по двум противоположным краям на упругие кольца. В динамической модели стенда кольца, балки и пластины рассматриваются как системы с распределёнными параметрами со своим спектром собственных частот. При разработке моделей используются понятия динамической жёсткости элементов и передаточных матриц, позволяющих унифицировать применение метода начальных параметров [7] и построить эффективный алгоритм расчёта. Динамическая жёсткость является функцией частоты и учитывает как упругие, так и инерционные свойства элемента, что существенно при воспроизведении на виброударном стенде испытательных режимов в частотном диапазоне до 10 кГц. Так как изгиб плит в такой конструкции близок к цилиндрическому, они могут рассматриваться как балки, опёртые по краям на кольцевые упругие элементы. При этом платформы стендов имеют высокую изгибную жёсткость и граничные условия на упругих опорах ближе к шарнирному опиранию. Система балок на упругих опорах составляет основу динамических моделей виброударных стендов взрывного действия.

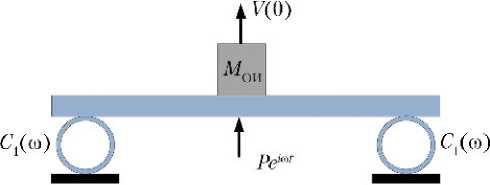
а)

♦ W

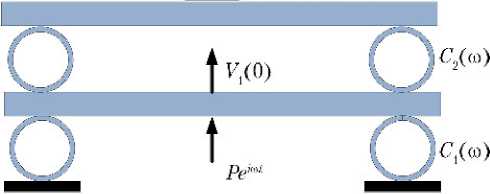
б)

Рис. 1. Схемы одноярусного (а) и двухъярусного (б) стендов взрывного действия: C ₁ ( ω ) , C ₂ ( ω ) — динамические (зависящие от частоты) жёсткости упругих колец, Н/м; V (0) , V ₁ (0) , V ₂ (0) — перемещения плит (балок) в середине пролёта, м; Pe^{i ω t} — гармоническая сила, Н; M_ОИ — масса объекта испытаний, кг

динамические жёсткости базовых элементов резонатора

Рассмотрим основные упруго-инерционные элементы резонатора стенда и определим их динамические жёсткости, которые конструктивно выполнены в виде наборов соосных колец и плит. Для определения динамической жёсткости кольцевого элемента рассмотрим вынужденные колебания кольца под действием гармонической силы Pe^{i ω t} , приложенной в полюсе (рис. 2, а )

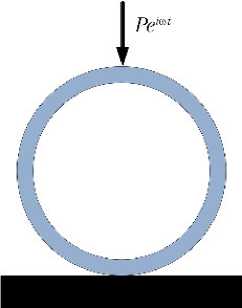
а)

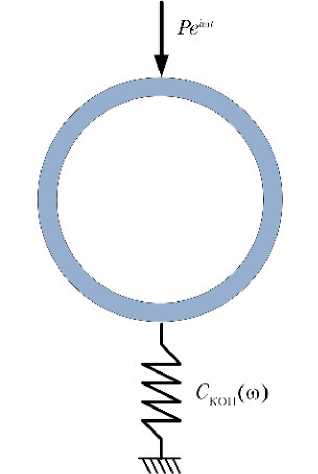
б)

Рис. 2. К определению динамических жёсткостей кольцевых элементов при неподвижном (а) и упругом опирании в нижнем сечении (б): Pe^{i ω t} — гармоническая сила, Н; С_КОП( ω ) — динамическая жёсткость опоры в точке контакта с упругим кольцом, Н/м

Пренебрегая растяжением нейтральной оси и тангенциальной компонентой сил

инерции, уравнение колебаний кольца примем в следующем кругового виде [8]:

∂³ M       1 ∂ M

+

∂ y ³          R ² ∂ y

M = – D _К

∂² w

_{∂ y 2} +

w

_{R 2}

;

∂ M

Q =^;

∂ y

∂³ w

– m

^К ∂ y ∂ t ²

= 0;

D К

E bh ³

12 (1 + in);

^m К

= ρ bh ,

где y = R ϕ — длина дуги нейтральной линии, отсчитанная от верхнего сечения кольца; R — радиус кольца; ϕ — угол, отсчитанный от верхнего сечения кольца; m _К — погонная масса кольца; h , b — толщина и длина кольца, соответственно; E — модуль упругости материала; t — время; w ( ϕ , t ) — прогиб нейтральной линии в каждый момент времени; D _К — комплексная изгибная жёсткость кольца; M , Q — изгибающий момент и перерезывающая сила в рассматриваемом сечении, соответственно; i — мнимая единица; η — коэффициент потерь на внутреннее трение, ρ — плотность.

Диссипативные свойства стенда определяются в основном внутренним трением в материале его упругих элементов, которые учитываются на основе модели комплексного модуля, или комплексной жёсткости [9]. Согласно этой модели изгибная жёсткость представляется в виде D _К = D _К ⁰ (1 + i η ).

Полагая в уравнении (1) w ( ϕ , t ) = V ( ϕ ) e^{i ω t} , где функция V ( ϕ ) определяет форму кривой, по которой изгибается кольцо при колебаниях, а ω — частота колебаний, получим уравнение для определения собственных частот и форм:

d5 V     d3 V   dV

+ 2        ⁺       (1 — ^X 4 ) = ^0;

дф       дф5    дф

λ⁴ = ^{m Кω2 R 4}

D _К ^.

Его решение:

V = A ₀ + A ₁sin a ϕ + A ₂cos a ϕ +

• + A ₃sh b ϕ + A ₄ch b ϕ ;

(2) a — у X² + 1;

• b — уУ X² - 1.

Для неподвижного нижнего сечения кольца (рис. 2, а ) решение (2) должно удовлетворять граничным условиям:

dV ∂ϕ

(0) = 0;

d³ V       PR ³

дфТ <°> = 1 d 7 ^; V ^{( n )} = ^0;

dV

∂ϕ

( π ) = 0 ;

π

∫ Vd ϕ = 0. 0

Если в нижнем сечении ( ϕ = π) кольцо опирается на упругий элемент (например — стержневую опору, поддерживающую стенд) с динамической жёсткостью в точке контакта С _КОП( ϕ ) (рис. 2, б ), третье граничное условие в условиях (3) заменяется следующим:

уравнению (4); D _Б — изгибная жёсткость балки (внутреннее трение материала учитывается моделью комплексного модуля); x — длина нейтральной линии, отсчитанная от середины пролёта балки (условие симметрии); внутреннее трение материала учитывается моделью комплексного модуля.

_d 3 _V

( π ) = ∂ϕ³

^{C ОП R 3} _{2 D К}

V ( π ).

Определяя постоянные интегрирования A ₀… A ₄ в решении (2), найдём амплитуду смещения в сечении, где приложена сила: V (0) = A ₀ + A ₂ + A ₄, и динамическую жёсткость кольца в точке ϕ = 0:

P

C ( to ) =-------------.                (4)

^К       A 0 + A 2 + A 4                  ⁽ )

Следующим базовым элементом резонатора является балка на упругих опорах, так как в плитах при их соединении, показанном на рис. 1, возбуждаются, в основном, колебания по балочному типу. Рассмотрим балку, опёртую по краям на упругие опоры, характеристики которых заданы своими динамическими жёсткостями C ( ω ), и определим динамическую жёсткость в центре балки. Ввиду симметрии рассматривается одна половина балки, нагруженная силой Pe^{i ω t} /2 (рис. 3).

Уравнение движения балки и граничные условия:

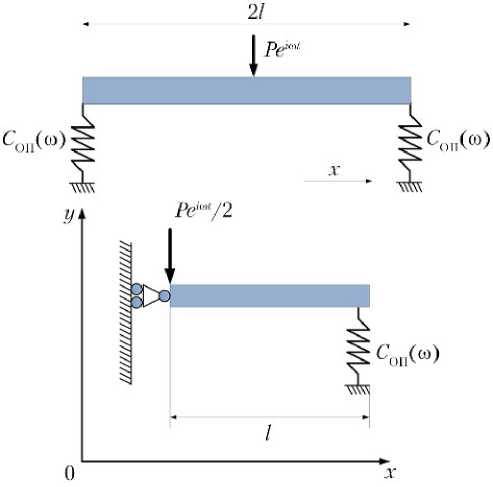
Рис. 3. К определению динамической жёсткости балки на упругих опорах: С_ОП( ω ) — динамическая жёсткость опоры, Н/м; Pe^{i ω t}/2 — гармоническая сила, Н; 2l — длина пролёта балки, м

Подчиняя решение уравнения (5)

w = C ₁ch α x + C ₂sh α x +

+ C ₃cos α x + C ₄sin α x;

α = ⁴ m ω² / D _Б

граничным условиям, найдём амплитуду прогиба балки в точке приложения

∂⁴ w

D

^Б ∂ x ⁴

∂² w

+ m Б _{∂ t 2} = 0;

нагрузки и, соответственно, динамическую жёсткость балки C _Б( ω ) на кольцевой опоре C _К( ω ):

∂3w               ∂2w x l:D б 1^ “ C <ю w =c ’ aF = 0

C Б ( ω ) =   _l 3 ^Б

4 µ ( ω )

2 α³ th ^α 2

α

x = 0 : D Б

_∂ 3 _w

∂ x ³

Peiωt,= 0,

1 +

µ ( ω ) α³

αα tg – th

. (6)

где C _К( ω ) — динамическая жёсткость кольцевой опоры, определяемая согласно

C ,» 1 ³ Здесь ц ( ю ) =   “    .

динамические модели стендов

Динамическая жёсткость балки на упругих опорах (6) по существу является основной динамической характеристикой одноярусного стенда, так как движение объекта испытаний, установленного по центру пролёта, описывается уравнением

М _ОИ y^.. + C _Б( ω ) y = P ( t ),

где М _ОИ — масса объекта испытаний; C _Б( ω ) — динамическая жёсткость балки на упругих опорах; P ( t ) — зависимость возбуждающей силы от времени.

Частотные передаточные функции по смещению и ускорению равны соответственно:

^Ф " ^{< m )} ■ с« ^:

Ф g ( to ) =

to2

С _б ( to ) •

Более сложно строится динамическая модель двухъярусного стенда. Как и ранее, определяющими формами колебаний, которые реализуются при нагружении в центре пролёта нижней платформы виброударного стенда (см. рис. 1), должны быть симметричные моды, что позволяет рассматривать одну половину системы ( x > 0), приняв в начале координат условия симметрии (рис. 4).

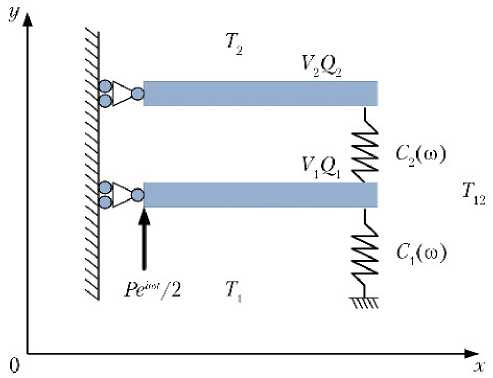
Рис. 4. Динамическая модель двухъярусного стенда: C₁( ω ), C₂( ω ) — динамические жёсткости упругих колец, Н/м; V_1,2, Q_1,2 — компоненты вектора состояния q _i — нижней (1) и верхней (2) балок, перемещение (м) и усилие (Н), соответственно; Pe^{i ω t}/2 — гармоническая сила, Н; T_1,2 — передаточные матрицы нижней (1) и верхней (2) балок; T₁₂ — матрица перехода от правого торца нижней балки к правому торцу верхней балки

Уравнения движения балок после

отделения времени:

d4V i dξ4

β i ⁴ =

- в⁴ v = 0; ii

m ω² l ⁴ i

D

i

Граничные условия на левом крае ξ = 0:

• V ₁ ′ = 0; V ₂ ′ = 0;

Q ₁ = D ₁ V ₁ ″′ = P /2;                     (8)

• Q ₂ = 0.

Условия сопряжения на правом крае ξ = 1/2:

M ₁ = 0; M ₂ = 0;

Q ₁ + C ₁ V ₁+ C ₂( V ₁ — V ₂) = 0;          (9)

Q ₂ — C ₂( V ₁ — V ₂) = 0.

Ввиду симметрии в дальнейшем будем использовать не общий вид решения типа уравнения (7), а только тот его частный случай, который удовлетворяет двум первым граничным условиям (8) и двум первым граничным условиям (9):

V ₁ = C ₁ ϕ ₁( ξ ) + B ₁ ψ ₁( ξ );

V ₂ = C ₂ ϕ ₂( ξ ) + B ₂ ψ ₂( ξ ), где

ϕ _i (ξ) = chβ _i ξ +

chβ _i /2

(ch β _i /2 + sin β _i /2)

× (shβ _i ξ – sinβ _i ξ);

ψ _i ( ξ ) = cos β _i ξ +

×

cos β _i /2

(sh β _i /2 + sin β _i /2)

× (sh β _i ξ – sin β _i ξ ).

×

Дальнейшее решение основано на методе начальных параметров в матричной форме [7]. В общем случае для балки вектор состояния в сечении имеет вид q _i = ( v_i , v_i ′ , M_i , Q_i ) ^T . Однако, в данном случае можно сократить число компонент вектора состояния и принять его в виде q _i = ( V_i , Q_i ) ^T , где в соответствии с уравнением (10):

V_i = C_i ϕ _i ( ξ ) + B_i ψ _i ( ξ );

Q_i = — C_iD_i ϕ _i ″′ ( ξ ) — B_iD_i ψ _i ″′ ( ξ ).

Введя вектор k _i = ( C_i , B_i ) ^T и матрицу

A . (О

Ф i ⁽0

- D . &"(£)

V i ⁽^

- D . V"'^)

Это соотношение необходимо конкретизировать с учётом граничных условий для обеих балок на левых краях (третье и четвёртое условия (8)):

перепишем соотношения (11) в виде qi(ξ) = Ai(ξ)ki.                          (12)

Выражая постоянные интегрирования (компоненты вектора k _i ) через компоненты вектора состояния на левой границе (через начальные параметры)

k _i = A_i (0) ^{— 1} q _i (0)

и подставляя полученное выражение в основное соотношение (12), получим связь между вектором состояния в произвольном сечении балки (в т. ч. на правой опоре) и вектором состояния на левой опоре:

q _i ( ξ ) = A_i ( ξ ) A_i (0) ^{— 1} q _i (0);

q _i ( l ) = A_i ( l_i ) A_i (0) ^{— 1} q _i (0).

Обозначим передаточные матрицы нижней и верхней балок:

T ₁ = A ₁( l ₁) A ₁(0) ^{— 1} ;

T ₂ = ( A ₂( l ₂) A ₂(0) ^{— 1} ) ^{— 1} .

Третье и четвертое условия (9) позволяют построить матрицу перехода от нижней балки к верхней через упру-

гие опоры:

V 2

e2

T

= T

f11) (Q i J

'c 1/C2 +1

-c 1

1/C 2"

-1

где T ₁₂ является матрицей перехода от правого торца нижней балки к пра-

вому торцу верхней. С помощью

построенных матриц можно установить связь между вектором состояния в левом сечении нижней балки, где при-

ложена внешняя сила, и вектором состояния в левом сечении верхней балки, где требуется определить амплитуду перемещения:

V 2

Q 2 0

= T

V 1

Q 1

( T = T ₂ T ₁₂ T ₁).

у v 2

= T

V 1

P /2

V 7

( T = T ₂ T ₁₂ T ₁).

Решая систему уравнений относительно двух неизвестных V ₁, V ₂, определим искомую амплитуду перемещения центрального сечения верхней балки:

V 2 (0) = у ( 1 12 — 1 11 1 - 1 22 ).

Отсюда следует, что динамическая жёсткость в центре верхней балки стенда C _БК( ω ) = P / V ₂ с учётом присоединённой массы объекта испытаний равна

C _Σ ( ω ) = C _БК( ω ) — М _ОИ ω ₂.

Частотные передаточные функции по смещению и ускорению равны, соответственно:

Φ _W ( ω ) =

Ф g ( to ) =

_{C Σ ( ω )} ;

ω2

c _s ( to ) •

вычисление ударного спектра

При испытаниях на виброударные нагрузки внешнее воздействие задаётся в виде ударного спектра, который должен реализовываться виброударным стендом взрывного действия. Внешнее воздействие создаётся с помощью взрывного устройства, при срабатывании которого реализуется апериодическое воздействие на стенд P ( t ), которое может быть представлено интегралом Фурье:

∞

S _P ( ω ) =           ∫ P(t)e^{i ω t}dt .

2 π ^–∞

Воздействия каждой элементарной гармонической силы S_P ( ω ) d ω на стенд происходят независимо, и их результаты могут быть суммируемы. Связь спектров входа (внешней апериодической силы от взрывного устройства) и выхода (ускорения на столе

стенда) определяется передаточными функциями (8) или (13):

S_G ( ω ) = Φ _G ( ω ) S_P ( ω ).               (14)

Спектр SG(ω) позволяет определить ударный спектр воздействия вибро-ударного стенда на объект испытаний. Традиционно он определяется без учёта массы и жёсткости объекта испытаний [4]. В этом приближении задача сводится к определению зависимости максимальных значений ускорения, которое получает «пробный» осциллятор, установленный на платформе стенда, от его собственной частоты. Примем уравнение такого осциллятора в виде y.. + 2δ y. + Ω2y = G(t), где G(t) — ускорение платформы стенда, и найдём связь между спектром амплитуд ускорений осциллятора и спектром ускорений платформы стенда:

s_Y< ш> =

го- S g го)

О² го- + 2 г 0 6

®^J®)

------—----S_p (to).

О to   Hi 0 6   ^p

Используя соотношение (14), можно связать спектры ускорений осциллятора и спектр возбуждающей нагрузки:

S_Y( to)-

го ф g to)

^ to- + 2 г 0 8

Sp. to ).

Обратное преобразование Фурье даёт:

y ( t , Ω) =

2 π

^∞ ω²Φ ( ω ) S ( ω )

^{G P}      e –i ω t dt.

–∞ Ω² – ω² + 2 i Ωδ

Ударным спектром по определению является функция

y ( Ω ) = max _t ( y ( t , Ω )).

экспериментальная апробация методики

С целью проверки предложенной расчётной методики проведены экспериментальные исследования на модели виброударного стенда с габаритномассовым макетом объекта испытаний (рис. 5).

Рис. 5. Виброударный стенд с габаритно-массовым макетом объекта испытаний

Результаты расчётов в сравнении с экспериментальными данными представлены на графике рис. 6.

В качестве исходной нагрузки принималось апериодическое воздействие силой 10 тс, длительностью 0,1 мкс, что соответствует нагрузке при использовании взрывчатых веществ. Как видно из рис. 6, предложенный аналитический подход позволяет спрогнозировать динамический отклик вибро-ударного стенда как по максимальной амплитуде ударного спектра, так и по частотному наполнению. Расхождение значений результатов эксперимента и аналитического решения объясняется идеализированным представлением аналитической модели по отношению к реальной конструкции виброударного стенда. Вместе с тем, с учётом требований нормативных документов к предельным значениям допусков на спектр удара ±6 дБ [5] по отношению к расчётному (эксплуатационному) уровню нагружения и с учётом погрешности измерения до 15% при измерении виброударных ускорений, полученные результаты подтверждают применимость аналитической модели для целей проектирования виброударных стендов и прогнозирования режимов виброударного нагружения бортовой аппаратуры.

Изложенная методика реализована в виде программы в среде Octave.

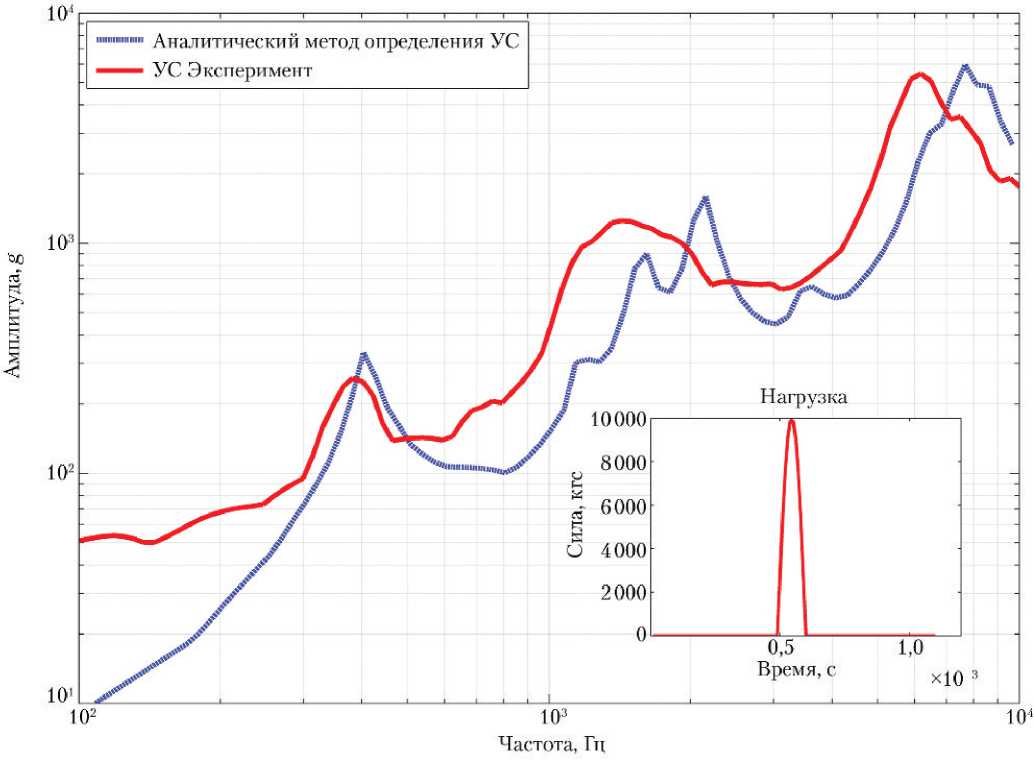
Рис. 6. Ударный спектр (УС), реализованный с использованием взрывного виброударного стенда, и результаты, полученные с использованием аналитической методики

выводы

Разработана и верифицирована методика определения динамических характеристик виброударных стендов взрывного действия для проведения предыс-пытательного моделирования и прогнозирования испытательных режимов.

Результаты работ могут быть использованы на этапе подготовки к проведению испытаний бортовой аппаратуры космических аппаратов на виброударные нагрузки и при проектировании виброударных стендов.