Методика проведения оперативного анализа электрических и временных параметров цифровых КМОП элементов и СБИС на их основе

и низких уровней напряжения для входных и выходных сигналов, зачастую, в отличие от аналоговых устройств, можно пренебречь достоверностью расчета переходных процессов. Таким образом при разработке цифровых устройств необходимо обеспечить допустимый компромисс между точностью моделирования (переходных процессов) и затратами временных ресурсов на разработку. Приемлемое снижение требований к точности расчета схем позволяет на этапе их моделирования переходить от транзисторного представления ЛЭ к более высоким уровням представления. Ниже рассматривается методика оперативного определения временных и мощностных параметров блоков КМОП СБИС и проведения их функциональной верификации, основанная на замещении логических элементов их макромоделями [3, 4].

Оперативный анализ параметров блоков КМОП СБИС. При разработке КМОП БИС часто необходимо проводить оценку и оптимизацию используемой архитектуры и схемноконструктивных решений путем «быстрого» оперативного анализа, но с приемлемой точностью. Проведение анализа и расчета многокаскадных КМОП схем на основе аналитической модели транзистора c физическими параметрами (пороговое напряжение, подвижность носителей, коэффициент влияния подложки и другие) не представляется возможным из-за сложности выражений, описывающих переходные процессы [2]. Для упрощения расчета цифровых схем на уровне логических элементов с незначительной потерей в точности целесообразно использовать макромодели ЛЭ – замещать ЛЭ «эквивалентными» инверторами (ЭИ).

Исходными данными при расчёте являются базовая задержка инвертора и емкости затворов, стоков и истоков транзисторов. Порядок расчёта состоит в следующем:

• -    замещение многокаскадной исходной схемы ЛЭ на цепочку с таким же числом каскадом ЭИ;

• -    определение параметров замещения ЛЭ на ЭИ;

• -    определение ширин каналов транзисторов ЭИ;

• -    определение ширин каналов транзисторов ЛЭ.

Расчет задержки распространения сигнала в каскадно-соединённых инверторах. Задержка распространения сигнала в инверторе определяется выражением:

t зад

К

Wn UН

du

/а • I'  -I' / pn

сигнала t^ ^exX и минимальна при t ф^(вх) =0, поскольку один из членов знаменателя в (1), равен 0. Суммарная задержка п каскадно соединенных инверторов (рисунок 1) зависит от соотношения длительности фронтов входного и выходного сигналов ( t фi^вxX , t фi^вькX ) каждого инвертора.

Можно показать, что задержка распространения сигнала в цепочке из n инверторов минимальна при:

(вх) _ ,(вых) фi фi , т.е., когда задержки отдельных инверторов равны, определяется выражением

где: С_Н - нагрузочная емкость инвертора; W n -

'

ширина канала транзистора n-типа; Ip, In - токи стока транзисторов n и р-типа с шириной канала равной единице; UH, UK - начальное и конечное напряжения при перезаряде емкости CH. От коэффициента а = Wp/ Wn (Wp - ширина канала МОП транзистора р-типа) зависит соотношение задержки положительного и отрицательного сиг налов (t ,t t и коэффициент а целесообразно выбирать из условия:

n

T . = Еt =nn■ t ,. зад      задi     задi i = 1

,

где t_3adi - задержка распространения i- го инвертора. При t фr^х фi^Oвьых^х . t фi^(вxX >t ф^^lxX - задержка распространения цепочки из n инверторов меньше (больше) суммарной задержки отдельных инверторов.

Оптимизация ширины каналов транзисторов КМОП инверторов. В общем случае выражение для нагрузочной емкости i- го инвертора имеет вид:

t ( + ) = t ( - ) зад зад

.

1"

С . = С. + yW. + у W..

Hi i        ii

Для инвертора на КМОП транзисторах можно считать, что а ■ I >> I при Ux< Unep и pn      вх пер а ■1p << In при Ux> Unep (здесь Uex - напряжение на входе инвертора, Unep - напряжение переключения инвертора. Поэтому, используя (1), условие (2) можно представить в виде

U       U пер du     пер du

Uh а • I      Uk I'

pn .

Из (3) получаем:

где C i - внешняя нагрузочная емкость; W, W_i+1 -ширины каналов транзисторов n-типа двух соседних инверторов.

Второй член в (6) представляет выходную, третий - входную емкость инверторов с номерами i и i+1 соответственно. Коэффициенты входной и выходной емкостей ( у' ', у ' ) при условии, если в качестве W i , W i+1 выбраны ширины каналов транзисторов n-типа, имеют следующий вид:

у ' = Св’ых + а • Св’ых np

,

= Свх + а • Свх np ,

где С_п ^вых , С_р ^вых , С_п ^вх , С_р ^вх выходная и входная емкости транзисторов n и p-типа с шириной канала, равной единице.

Задержку инвертора представим в нормированном виде:

U     U пер du пер du а = J — / J Uн IpUк In

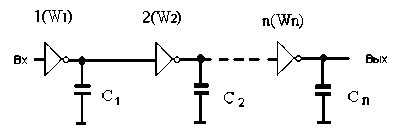
Рис. 1. Цепочка инверторов

t t      = зад-i зад.1   t зад.0

,

Задержка распространения сигнала на инверторе зависит от длительности фронта входного

где в качестве нормировочной величины (t₃ aд. ₀) выбрана задержка одного инвертора в цепочке последовательно соединенных инверторов с одинаковыми топологическими размерами (базовая задержка). Эта задержка является характеристикой технологии изготовления КМОП СБИС и

легко может быть определена экспериментально или расчётно. Отметим, что для инверторов с одинаковыми топологическими размерами транзисторов n-типа, выражение (6), при Ci =0 приводится к следующей форме:

Поскольку для цепочки одинаковых инверторов с C_i=0 при i= 1,2,3 ,... n -1, Y^ = Y , ^у = Y , ^t_зад_i = t_3ag при i= 1, 2, 3 ,... n, для последнего инвертора выражение (12) принимает вид

C ■ = (Y + Y )- W- нi                 i

W n

Учитывая (1), (6), (10) выражение (9) можно записать в виде:

C

i

^{( t} задi " ^{( Y + Y} ) ^{- Y} i )

_____ у'.-W . + г ," W.  ,+ C. t = i i i + 1 i + 1 i ^задi          (y + y ) - W

где: C i - внешняя нагрузочная емкость последнего каскада; W_n - ширина канала транзистора n-типа последнего каскада.

Из (5) с учетом (11) получим выражение для нормированной задержки цепочки из n инверторов:

Решая (11) относительно W i , получим формулу для расчета ширин каналов транзисторов в инверторах, начиная с последнего инвертора (при заданной нагрузке Ci и задержке z^. на каскад):

ⁿ         W +1 C

T , =--У Y + Y . - —i+1 + -i- зад г . \ ■ л i i +1 W    W

⁽Y + Y ) i = 1 (            W   Wi J

C. + y "  .- W .

i i + 1 i + 1

tзадi " ^{( y + Y} ) ^{- Y} i

•

где W_i+1 =0 при i=n .

Минимум нормированной

задержки при

.³“^д = 0 ( i= 1,2,3,. n ), т.е. оптимальные значения d W

г ширин каналов транзисторов по быстродействию находятся из решения следующей системы уравнений:

Y. - W ² - Y-  1" W-  1" W-  1- C. - W. .= 0, для i = 2, 3,, n-1;

'i i ' + + 1 i - 1 i + 1 i i - 1     ’                ’  ’    ’

Y. - W ² - C. - W.  , = 0, для i = n.

I i i      i i ^{- 1}                                                                                (15)

Однозначное решение системы (15) можно получить, если задаться геометрическими размерами транзисторов одного из каскадов, как правило, первого Wi или последнего Wn. Для цепочки инверторов с Ci=0 при i =2,3,., n-1; Ci^0 при i=n и Yz= Y,Yz- = Y при i=2,3,., n, задержка T минимальна, если равны задержки отдель- ных каскадов

tзадi = ?зад • Из (15) имеем в этом случае следующую связь между ширинами каналов транзисторов трех соседних инверторов:

W. = / W.  ,- W.  , i у i-1 i +1

(i= 2, 3,. , n-1).

Следовательно, (13) позволяет найти оптимальные ширины каналов транзисторов цепочки инверторов, исходя из заданной задержки т^ ^, равно распределённой по всем каскадам. Отметим, что реализация решения системы (15) на ЭВМ позволяет оперативно проводить приближенную оптимизацию схемы на дополняющих КМОП транзисторах по быстродействию.

Параметры замещения логических элементов. Логический элемент состоит из ветвей n и p-типа транзисторов, подсоединённых к выходу [5, 6]. Каждая ветвь может содержать последовательные и параллельные транзисторы одного типа, при этом количество транзисторов в ветвях может быть различно [7, 8]. Наибольшее время переключения определяется ветвью, которая содержит максимальное число последовательно соединённых однотипных транзисторов. Данными для определения параметров замещения ЛЭ являются:

• -    электрические схемы ЛЭ на уровне транзисторов ;

• -    эскиз топологии ЛЭ;

• -    t_зад . ₀ - базовая задержка инвертора;

• -    С _п ^вх , С рв - входная емкость транзисторов n, p-типа с шириной канала, равной единице;

• -    С_п ^вых , С_р ^бых - выходная емкость транзисторов n, p-типа с шириной канала, равной единице;

• -    коэффициент а ;

• -    коэффициент выходной емкости инвертора у' ;

• -    коэффициент входной емкости инвертора y" •

В рассчитываемой схеме каждый ЛЭ замещается своей макромоделью. Для проведения расчёта необходимо определить следующие параметры замещения ЛЭ на ЭИ:

Y'экв - коэффициент выходной емкости;

Y "экв - коэффициент входной емкости;

а_экв - коэффициент, равный отношению эквивалентной ширины каналов транзисторов п и р- типа в ЭИ.

Задача расчета параметров ЭИ сводится к определению размеров транзисторов ЭИ, при которых обеспечивается заданное быстродействие замещаемого логического элемента. Ширины каналов транзисторов W_nэкв и W_pэкв эквивалентного инвертора ЭИ с целью удобства при расчетах будем характеризовать одним параметром - шириной каналов транзисторов п- типа W_n3KB. Опустим индекс п , обозначив:

Для У экв i - коэффициента выходной емкости i-го ЭИ в согласно уравнению (7) получим:

Y == Свых..+ a . -Свых экв .г     пэкв .г    экв.г   рэкв .г

где

тогда для i -го ЭИ

W = W , экв.    п. экв

вых пэкв .1

= (1/ к .) • Q - V --Свых ni ni ni n

,

вых рэкв .г

= (1/ K )Q - V --Сых pi pi pi p

,

W„   .= a .W ., рэкв .г.     экв .г   экв.г

где a_экв . _i - эквивалентный коэффициент ЭИ, определяемый по формуле:

K pi a = = a •—£— экв .г     к ni ,

где: K_ni - суммарное число транзисторов п- типа в последовательной ветви ЛЭ с максимальным количеством транзисторов, подсоединённой к выходу; K_pi - суммарное число транзисторов р- типа в последовательной ветви ЛЭ с максимальным количеством транзисторов, подсоединённой к выходу.

Определим коэффициенты входной и выходной емкостей ЭИ. Для у" _{ - коэффициента входной емкости i -го ЭИ, согласно уравнению (8) получим:

Y ' ^= Свх  ,+ a экв .г     пэкв .г    экв .г		Cвх рэкв .г	(19)
где
Cвх пэкв .г = ээкв . i	- С вх n	,	(20)
Cвх рэкв .г = W экв .i	- С вх p <	•	(21)

Тогда уравнение (19) с учетом уравнений (18, 20, 21), примет следующий вид:

K у'  . = W .свх + a--^-W  --Свх экв. г     экв .г   п       к      экв .г   р ni

.

z ni

V .= Z A .

ni         nj

J = ¹

,

z zpi

V • = У A ■ pi         pj

J = ¹

где: Q_ni , Q_pi - суммарное количество транзисторов п и р- типа подключенных к выходу i -го ЛЭ, V_ni , V pi - коэффициенты для ветви с максимальным числом последовательно соединённых транзисторов п, р- типа подключенными к выходу i -го ЛЭ, содержащей Z„ , Z_pi узлов, A j A pj - суммарное число стоковых или истоковых областей, подключенных к j- узлу, рассматриваемой последовательной ветви.

Подставив (18), (24), (20) в (23) получим коэффициент выходной емкости i -го ЭИ:

K у . = (1/K .)Q .-V.-Свых + (1/K .)Q -V -•a-РСвых экв .г       пг пщ  пг п         рг р рг  рг к Р ni

Определение ширины каналов транзи сторов ЛЭ. Учитывая, что t ,.= R    /у'    ■=R • K .-(1/Q ,)у'    .;

зад.г    экв.г  экв.г    п пг    пщ   экв .г t л = = R -(у’+у"); зад.0    п то можно собственную нормированную задерж ку ЭИ t ,  ,   ., замещающего i-й ЛЭ, можно зад.соб.экв.г представить, согласно уравнению (9), следующим образом:

   Rn• ^™-(1/й.1)-Гэкв.    Кт ' Вт>?,кв.г t                 =                                             '

зад.соб . экв.г          ^R n -⁽у + у )       =       ( у + у )

Нормированную задержку ЭИ, замещающего i -й ЛЭ, с учетом внешний нагрузки представим в следующем виде:

________ Кш--(1/Q„ Л-у .W . + C t          = n1 v nn'экв.г   экв.г н зад.экв.1               z ' , "ч тт/

( у + у ) - W экв .

Решая (29) относительно W экв.i , получим формулу для расчета ширины канала транзистора ЭИ:

C

W - =        —;---Н-^-----------;--- экв '  tsads кв в"(7+ 7 ) - К™ '(1/Qni )Y3K6i за .ээкв.н                            экв.i    ( 30)

Ширины каналов транзисторов последовательной цепи ЛЭ (с числом транзисторов, равным Кni ) определяются по формуле:

W ⁽ ЛЭ ) = К _w . ni          ni    экв .i

.

Ширины каналов транзисторов р- типа ЛЭ определяются по формуле

W ⁽ ЛЭ ) = a • -^ i • W ⁽ ЛЭ )

рi        K    ni ni

.

Выводы: в статье подробно описана методика оперативного расчета параметров КМОП цифровых ЛЭ и схем на их основе, основанная на использовании макромодели с фиксированным набором параметров для замещения всех ЛЭ схемы, в независимости от функционального назначения элемента. Рассмотренная методика расчета КМОП схем позволяет:

• -    упростить и ускорить расчет задержек распространения сигналов в цепях;

• -    определять геометрические размеры транзисторов по заданным задержкам распространения сигналов;

• -    проводить оптимизацию схем по площади, занимаемой на кристалле.

Перечисленные выше возможности обеспечивают проведение оперативного анализа используемых схемно-конструктивных решений логических элементов и цифровых блоков с целью выполнения следующих задач:

• -    выявление критических путей распространения сигналов;

• -    оптимизация задержек распространения сигналов по критическим путям;

• -    выбор оптимальных по площади, занимаемой на кристалле, ЛЭ;

• -    оценка реализуемости схемы на соответствие техническому заданию.

Предварительный анализ КМОП схем на основе положений настоящей методики предоставляет возможность формирования данных для расчёта схем стандартными традиционными методами схемотехнического моделирования с использованием САПР.