Методика расчета коэффициента использования мультисервисных сетей

Современные компьютерные сети предоставляют широкий спектр мультимедийных услуг, в том числе IP-телефонии, IPTV и видеоконференций. Обеспечение качества обслуживания QoS (Quality of Service) при доставке мультимедийного трафика реального времени подразумевает соблюдение требований к максимальной задержке передачи, а также обеспечение гарантий по доставке трафика без потерь. Это может достигаться за счет резервирования ресурсов сети и контроля допуска мультимедийных сессий. При передаче пульсирующего трафика, в частности, видеопотока с переменной скоростью VBR (Variable Bit Rate), определение необходимого объема резервируемых ресурсов является весьма сложной задачей. С одной стороны, выделение пропускной способности в расчете на среднюю скорость VBR-потока приводит к недопустимым задержкам или потерям пакетов, а с другой стороны, резервирование в расчете на максимальную скорость значительно снижает коэффициент использования сети. Одним из распространенных подходов к обеспечению QoS является детерминированное обслуживание. Данный подход обеспечивает строгое соблюдение требований к QoS на основе детерминированного описания потоков данных и узлов сети.

В настоящей работе рассмотрена методика расчета пропускной способности мультисервисной сети и выведен коэффициент ее использования при детерминированном обслуживании группы VBR-потоков. Для этого использованы соответствующие детерминированные модели видеопотоков, сжимаемых в соответствии со стандартом H.264, модели узлов сети, а также критерий допуска сессий, определяющий максимальное число потоков в сети. Исследование показало преимущество данного подхода к управлению сетью по срав- нению с планированием на основе пиковой или средней скорости потоков и в то же время позволило выявить наличие потенциала для возможного увеличения коэффициента использования сети, например, за счет использования стохастических моделей. В работе также показано, каким образом с помощью предложенной методики можно оценивать эффективность алгоритмов планирования и регулирования трафика в сетях с интегрированным обслуживанием.

Модели сетей с детерминированным обслуживанием

Используемые в данной работе методы и алгоритмы опираются на теорию сетевого исчисления [1], согласно которой каждый входной поток данных и каждый элемент исследуемой сети описываются детерминированными моделями, характеризующими поведение объекта в «худшем случае». На их основе определяются свойства выходных потоков и параметры качества обслуживания. Рассмотрим математическую модель передаваемого трафика, необходимую для расчета коэффициента использования сети. Будем считать, что каждый поток задается кумулятивной функцией поступления A _{( t )}, определяющей объем данных, переданных к моменту _t. Для учета динамических свойств трафика (всплесков, периодов наибольшей активности и т.п.), а также с целью обеспечения гарантий его передачи введем функцию, определяющую максимально возможный объем данных, передаваемых на произвольном интервале времени. Такую модель назовем кривой поступления α( t ) и определим неравенством

Л(т + /)-Я(т)< a(/), Vt . (1)

Далее рассмотрим узел сети доступа, обслуживающий поток A(t). Будем считать, что выходной поток этого узла описывается кумулятивной функцией W(t). Тогда разность 40-НО определяет объем данных, находящихся в очереди рассматриваемого узла. Эти данные будут полностью переданы к некоторому моменту времени t', для которого выполняется неравенство W(t') > A(t). Интервал времени t' – t является задержкой передачи в момент t. Для того чтобы удовлетворить требование по максимально допустимой задержке передачи, нужно за время t гарантировать предо- и определяется как tf(/)

ставление потоку A ( t ) минимально необходимой пропускной способности канала. Соответствующая модель называется кривой обслуживания β(τ) > inf se[O.f

)+P(/-5)}.

Теперь рассмотрим пару функций, увязывающих кривые поступления и обслуживания с параметрами QoS, которые обеспечивает рассматриваемая сеть. Назовем максимальным горизонтальным расстоянием между α( t ) и β( t ) функцию вида

/?(а, P) = sup{inf {т > 0: a(s) < p(s + t)}}, (2) s>0

а максимальным вертикальным расстоянием между α( t ) и β( t ) – функцию v(a,p) = sup{a(s)-p(s)}.

Из теории сетей следует, что для трафика, характеризуемого кривой поступления α( t ), и сервера, характеризуемого кривой обслуживания β( t ), максимальная задержка любого бита входного потока составляет h(α, β), а размер очереди сервера не превышает υ( t ). Так как эти уравнения связывают параметры QoS с объемом предоставляемых ресурсов, то их можно использовать для вывода критерия допуска сессий в сеть передачи. Этот критерий, в свою очередь, позволяет определить максимальное количество соединений при известных максимальных скоростях узлов сети.

На практике применению точных детерминированных моделей препятствует высокая вычислительная сложность связанных с ними алгоритмов профилирования и контроля допуска. Как правило, в качестве кривых поступления и обслуживания используются функции простого вида (например, регулятор «дырявое ведро», описываемый кусочно-линейной функцией), которые приближенно характеризуют исследуемую сеть. Одним из подходов к обеспечению детерминированного QoS является интегрированное обслуживание IntServ (Integrated Services) [2]. В рамках сети IntServ для предоставления строгих гарантий доставки и задержки передачи используется метод гарантированного обслуживания GS (Guaranteed Service) [3], определяющий правила описания сети и трафика.

Рассмотрим работу GS-сервера при детерминированном обслуживании трафика реального времени. На входе в сеть IntServ каждый поток данных профилируется по алгоритму «дырявого ведра», и параметры потока передаются GS-серверам с помощью дескриптора TSpec. Каждый дескриптор включает в себя следующие элементы: b – глубина «дырявого ведра», то есть максимальный размер всплеска в потоке; r – скорость опустошения «дырявого ведра», то есть долговремен- ная средняя скорость потока; M – максимальный размер кадра в потоке; p – максимальная скорость канала, обслуживающего данный поток.

Дескриптор ( b , r , M , p ) задает кривую поступления a(/)= min(/>Z + M,rt + Z>), ограничивающую объем трафика в соответствии с неравенством (1). Согласно спецификации, такому потоку предоставляется пропускная способность, определя-

C емая скоростью R и задержкой D + — . GS-сервер R с такими параметрами гарантирует передачу с задержкой меньше чем — + — + D . Параметр R R R может быть интерпретирован как скорость виртуальной выделенной линии, предоставляемой потоку. При этом указанное требование по максимально допустимой задержке выполняется при условии, что скорость R не ниже средней скорости r передаваемого потока. Выбор значения параметра R > r в зависимости от требований к QoS позволяет либо уменьшить задержку, либо увеличить коэффициент использования сети за счет меньшего объема резервируемых ресурсов.

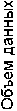
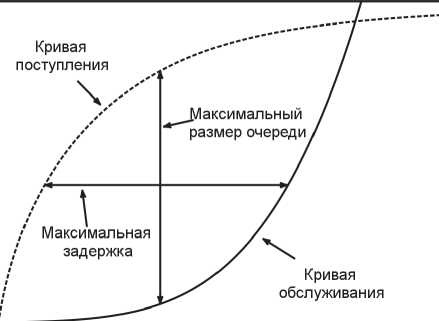
Рис. 1. Типичные кривые поступления и обслуживания

Параметры C и D определяют дополнительные задержки по отношению к реальной выделенной линией, а именно: постоянную и зависящую от скорости передачи. Пара параметров C и D определяет множество возможных кривых обслуживания GS-сервера

P(?) = max 0,7? t---DI I 7?

где параметр R >  r . Типичные для GS-сервера кривые поступления и обслуживания показаны на рис. 1.

Установка соединения в сети IntServ завершается резервированием некоторой части R пропус- кной способности GS-сервера на пути передачи потока данных. Величина R должна определяться исходя из требований к задержке передаваемого трафика. Эта задержка может быть вычислена на основе данных, содержащихся в дескрипторах TSpec и AdSpec:

эта функция является огибающей последовательности значений кумулятивной функции A ( t ):

E^ = тах(л(т + /)-Л(т)) V/> 0.

b-M

R

p- R p-r

M + C

R

+ D при p> R>r.

При одинаковых параметрах дескрипторов Tspec у всех потоков и достаточности пропускной способности c GS-сервера получаем ограничение на количество передаваемых потоков:

^d - D\p - r^-v^b - M^ p^b — M^ + (C + M^p — r)

при p> R>r.

Это неравенство позволяет осуществить выбор алгоритмов пакетного планирования и регулирования, обеспечивающих наиболее эффективное использование сетевых ресурсов при заданных требованиях к QoS, а также дать интегральную оценку методу IntServ.

Характеризация передаваемого трафика

Для расчетов параметров сети и оценки эффективности передачи трафика в качестве типовых используем фрагменты видеозаписей из открытой онлайн-библиотеки [4]. Каждый фрагмент содержит в себе информацию о кадрах 30-минутного оцифрованного видеоролика, сжатого в соответствии со стандартом H.264. Эта информация включает в себя тип кадра (I, P, B в терминологии кодировании MPEG), его размер, а также время генерации. В экспериментах, описываемых в данной статье, использованы фрагменты записей «Terminator 1» и «NBC News», которые в дальнейшем будем называть просто «фильм» и «новости».

Согласно ранее рассмотренной модели каждый поток описывается кривой поступления α( t ), ограничивающей сверху объем данных, переданных источником на интервале времени t . Поскольку исследуются всего лишь отдельные фрагменты видеопотоков, для произвольного значения t точная характеристика источника, очевидно, получена быть не может. Поэтому вместо (точной) кривой обслуживания используется приближенная характеристика, называемая эмпирической огибающей E ( t ) [5] и вычисляемая на основе данного фрагмента трафика. По определению

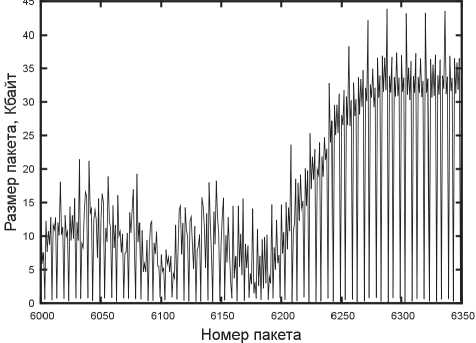
Рис. 2. Фрагмент потока «фильм»

Рассматриваемые видеофрагменты представляют собой последовательности кадров размером VVJ2.../NL полученных с интервалом пакетизации T . Для этого потока значения эмпирической огибающей в моменты времени iT вычисляются как

k+i

E(i-T^= max V f, для z = l,2,...,vV. (4) 0<к<К-!+1^—р

J=k

При этом значения функции для iT < (/ +1)7 будем считать равными £(zT) . На рис. 3 показаны функция поступления и эмпирическая огибающая для потока типа «фильм», фрагмент которого представлен на рис. 2.

С целью определения, в частности, параметров сети IntServ на основе полученной эмпирической огибающей рассчитаем для каждого видеопотока параметры дескрипторов TSpec. По стандарту параметры M и p из четверки ( M , p , b , r ) характеризуют канал передачи источника данных и не зависят от свойств самого трафика. Поэтому для описания потока данных достаточно пары ( b , r ), задающей кривую поступления a(z) = r -t + b . Существенно отметить также, что это же ограничение накладывается на трафик с помощью регулятора «дырявое ведро». Следовательно, определение дескриптора TSpec сводится к подбору параметров «дырявого ведра», пропускающего рассматриваемый поток без дополнительной задержки. Значения остальных параметров ( M и p ) могут быть заданы для описания специфических условий эксперимента при необходимости.

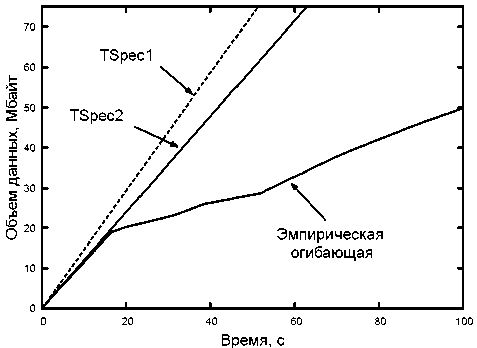
Рис. 3. Детерминированные характеристики потока «фильм»

Приведем алгоритм вычисления параметров ( r , b ) дескриптора TSpec на основе известной эмпирической огибающей. Так как огибающая E (t) является минимальной ограничивающей функцией для рассматриваемого потока, то кривая поступления для «дырявого ведра» с параметрами ( r , b ) ^а_гА^=^г^^+ь удовлетворяет неравенству a_rb^> Е^ Vt . В качестве дополнительного условия примем, что на интервале, равном времени пакетизации, кривая α _r,b( t ) совпадает с E ( t ): a_rb(T)=E(T). Далее рассмотрим множество линейных функций «,,_т^=Р.Т + ^_п , где n g [2,TV]. Для каждой функции «„rW справедливы следующие равенства: