Методика расчета констант упругости наклонного смектика

Жидкие кристаллы – это материалы, обладающие электрооптическими свойствами кристаллов, но при этом вязко-упругими свойствами жидкостей. Это позволяет использовать их во многих приложениях, в частности, в дисплейной технике. На рис. 1 приведены несколько жидкокристаллических фаз. В современных дисплеях используются жидкие кристаллы, находящиеся в нематиче-

(a)                   (b)

Рис. 1. Жидкокристаллические фазы: нематик (a); смектик-A (b); смектик-С (с)

(c)

ской фазе (рис. 1 (a)). В этой фазе молекулы жидкого кристалла обладают ориентационным порядком, но трансляционный порядок (по положению центров масс молекул) отсутствует. В современных разработках предполагается использование наклонных смектиков (рис. 1 (с)), которые обладают гораздо более высоким быстродействием и более низким энергопотреблением, поскольку при переориентации во внешнем поле они испытывают наиболее легкий тип деформации: продольный изгиб и кручение при движении молекул по конусу. Во многих приложениях требуется рассчитать упругие свойства смектических материалов [1].

Рассмотрим наклонную смектическую структуру, обладающую идеальным смектическим порядком (т.е. центры масс всех молекул расположены строго в определенных смектических слоях). В то же время, мы не будем предполагать, что нематический порядок в смектических слоях идеален. Внутреннюю энергию системы, приходящуюся на один смектический слой i в расчете на единицу его поверхности можно записать в следующем виде [2, 3]:

Ei = 2 P 21Ш f (a1 ■ n1) f (a2 ' n2 ) g (r1, r2 ) Ue. ( a1, a2, r12 ) d 2a1 d 2r1 d 2a2 d 2r2 , (1) где ρ – поверхностная плотность молекул в смектическом слое, Uef12 (a1,a2,r12) – эффективное взаимодействие между молекулами 1 и 2, ориентация длинных осей которых представлена еди- ничными векторами a1 и a2 соответственно, и положения центров масс которых в плоскости смектических слоев задается векторами r1 and r2, соответственно. Вектор r12 = r2 – r1 есть проекция межмолекулярного вектора на плоскость смектического слоя. Полная внутренняя энергия системы, приходящаяся на один смектический слой, предполагает, что молекулы 1 и 2 могут принадлежать как одному, так и соседним слоям. Директор нематического порядка может изме- няться как от слоя к слою, так и в пределах одного слоя, так что в системе допускается присутствие всех трех типов деформаций: кручения, продольного изгиба и поперечного изгиба, поэтому единичные векторы n1 и n2 определяют направления нематического директора в точках 1 и 2, соответственно. Единичные векторы a1 и a2 определяют направления принципиальной вытянутости молекул. Функции распределения длинных осей молекул по ориентациям f(a1∙n1) и f(a2∙n2) подразумеваются не зависящими от положения молекул, а распределение g(r1,r2) молекул 1 и 2 по их взаимному расположению предполагается не зависящим от их ориентаций. Разумно предположить, что корелляционная функция g(r1,r2) зависит только от проекции межмолекулярного вектора на плоскость смектического слоя r12. Интеграл по положению второй молекулы r2 в формуле (1) (которое для простоты может отсчитываться от положения первой молекулы, т.е. r2 = r12) разделяется на угловую и радиальную части: d2r12 = r12 dr12 du12, где u12 – единичный вектор вдоль направления, соединяющего центры масс молекул. В последующих разделах интеграл, представленный в формуле (1), будет рассмотрен отдельным образом для точек 1 и 2, принадлежащих одному и тому же смектическому слою, и для точек, принадлежащих соседним слоям, и мы пренебрежем взаимодействием молекул, находящихся в более далеких слоях.

Аппроксимация внутренней энергии отдельного смектического слоя

Поскольку эффективный потенциал взаимодействия U^ef 12 ( a ₁ , a ₂ , r ₁₂) резко убывает с увеличением расстояния r ₁₂ между молекулами, находящимися в одном смектическом слое, то слабо меняющаяся с расстоянием корелляционная функция g ( r 12 ) может быть вынесена из-под знака интеграла r ₁₂ в рамках метода перевала [4]:

w                                            w j g ( r12 ) Uef ( a1’ a2’ r12 ) r12 dr12 ~ g (§12 (a1’ a2’ u12 )) J U\f ( a1’ a2’ r12 ) r12 d r12 ’              (2)

где ξ ₁₂ – минимальное расстояние между молекулами для данной конкретной ориентации молекул и межмолекулярного вектора. Поскольку ориентационные функции распределения f ( a ₁ ∙ n ₁ ) и f ( a ₂ ∙ n ₂ ) более резко убывают при отклонении ориентации молекул от наиболее вероятных направлений, чем корреляционная функция распределения, а также, поскольку деформация нематического директора в пределах одного и того же смектического слоя ощутима только на больших расстояниях по сравнению с размером молекулы, то корреляционная функция g ( r 12 ) может также быть вынесена и из-под знака интеграла по ориентациям молекул в формуле (1):

w

J J d ^a 1 d ^a 2 g ⁽ ^ 12 ^{( a} 1 , ^a 2 , u 12 ) ) J ^{f ( a} 1 ' n 1 ) ^{f ( a} 2 ' ⁿ 2 ) U ef ^{( a} 1 , ^a 2 , ^r 12 ) ^r 12 d r 12 ~

w

» g ( § 12 ( a 1 || a 2 , u 12 ) ) JJ d ² a 1 d 2 a 2 J f ( ^a 1 ■ n 1 ) f ( ^a 2 ■ n 2 ) U^f ( a 1 , a 2 , ^r_n ) r_X 2 dr_X 2 .

Аппроксимируем эффективный потенциал Uef12 (a1, a2, r12) в формуле (3) ортонормированной системой сферических инвариантов TℓLλ(a1,u12,a2) [5, 6]:

U ef ^{( a} 1 , ^a 2 , ^r 12 ) = - ^ J lLX ^{( r} 12 ) T lLX ^{( a} 1 , ^u 12 , ^a 2 ) •                        ⁽⁴⁾

l , L , λ

Подставляя выражение (4) в формулу (3), используя свойство сферических инвариантов и принимая во внимание формулу (1), получаем следующее выражение для внутренней энергии отдельного смектического слоя:

^Eii ”"? P 2 J d u 12 g ( ^ 12 ( ^a 1 ^{|| a} 2 ’ u 12 ) ) E ⁵1 S X J [ J lLX ( ^r 12 ) ] Tt LX ( ⁿ ( ^r 1 ) , ^u 12 , ⁿ ( ^r 2 ) ) ^r 12 ^dr 12 , ⁽⁵⁾

2                                        l,L,λ0

где S ℓ – параметры нематического порядка [1–3]:

S। =Jf (a • n ) P| ( a • n ) d2a ’(6)

где функция P ℓ есть ℓ -тый полином Лежандра. Производя также интегрирование по вектору u 12 в формуле (5), еще раз пользуясь свойством сферических инвариантов, и учитывая, что в случае идеального смектического порядка

^L = P J g (§12 (u12 • k)) PL (u12 • k) d u12 = ^0 PL (0) , a1||a2

где σ 0 – число ближайших соседей у произвольной молекулы в смектическом слое (около шести), вектор k есть нормаль к плоскости смектического слоя, и где интегрирование по вектору u 12 фактически соответствует интегрированию по одному углу, который описывает ориентацию межмолекулярного вектора в плоскости смектического слоя, получаем:

Eii ~ -T P E 51 °L SX J JlLX ( r12 ) TlLX (n (r1) ’ k’n ( r2 )) r12 d r12 •

• 2    l,L,λ0

Выражение (8) представляет собой внутреннюю энергию отдельного смектического слоя. В частности, она определяет наклон молекул в смектическом слое, а также упругость смектического слоя по отношению к деформации поперечного изгиба.

Серия «Математика, физика, химия», выпуск 11

Аппроксимация взаимодействия соседних смектических слоев

При рассмотрении взаимодействия молекул, находящихся в соседних смектических слоях, мы можем наоборот воспользоваться предположением о том, эффективное взаимодействие гораздо меньше меняется при изменении межмолекулярного r ₁₂, чем корелляционная функция

g(r12) и орентационные функции распределения f(a1∙n1) и f(a2∙n2). Действительно, корелляционная функция g(r12) имеет резкий максимум для такого расположения молекул, при котором их хвосты в соседних слоях соприкасаются. Ориентационные же функции распределения f(a1∙n1) и f(a2∙n2)

имеют резкие, когда каждая из осей строго смотрит вдоль своего директора. Тогда в рамках ме- тода перевала эффективное взаимодействие может быть вынесено за знаки всех интегралов в формуле (1):

P JJJ ^f ( a l ■ n 1 ) ^f ( a 2 ' n 2 ) g ( r 12 ) ^Uf ( ^a 1 ^{, a} 2 ^, r 12 ) d 2 a 1 d 2 a 2 d 2 r 12 » U ef ( n i , n 2 , § 12 ( n i , n 2 , k ) ) J pg ( r i2 ) d 2 r i2 ,

где направление вектора ξ 12 определяется максимумом корелляционной функции g ( r 12 ). По аналогии с формулой (4), запишем аппроксимацию эффективного взаимодействия молекул в соседних смектических слоях сферическими инвариантами:

U if ⁽ n l , n 2 , § 12 ⁽ n l , n 2 , k ) ) = - ^ J lLX T lLX ⁽ n i , k , ⁿ 2 ) •                       ⁽¹⁰⁾

l , L , λ

Заметим, что интеграл во второй строке формулы (9) равен просто единице, поскольку вторая молекула с достоверностью должна занимать какое-то место в слое над первой молекулой. Принимая это во внимание и подставляя выражения (9) и (10) в формулу (1), получаем для энергии взаимодействия двух соседних смектических слоев:

E i , i ± 1 ~- 2 ^P ^ J lLX ^{ T lLX ^{( n} i - 1 , k , ⁿ i ^{) +} T l LX ^{( n} i , k , ⁿ i + 1 ^)} • ⁽¹¹⁾ l , L , λ

Выражение (11) представляет собой энергию взаимодействия соседних смектических слоев. В частности, она определяет упругость смектического слоя по отношению к деформациям кручения и продольного изгиба.

Деформация поперечного изгиба K 11

Сопротивление деформации поперечного изгиба в смектическом состоянии определяется, в основном, взаимодействиями молекул внутри смектических слоев. Выражение (8) для внутренней энергии отдельного смектического слоя, в частности, описывает сопротивление смектика поперечному изгибу. Запишем выражение для градиентного разложения нематического директора n ( r 2 ) в точке 2 (обе точки 1 и 2 расположены в одном и том же смектическом слое), подразумевая деформацию нематического директора в смектическом слое малой:

n ( Г 2 ) = n ( ^r i ) + ( Г 12 -V ) n ( ^r i ) + ¹ ( Г 12 -V ) ² n ( ^r i ) + к ⁽¹²⁾ Учитывая, что вектор r 12 параллелен вектору деформации поперечного изгиба, можем исключить ориентацию вектора r 12 из формулы (12):

n ( Г 2 ) = n ( ^r i ) + r i2 ^V r ₁₂ n ( ^r i ) + ¹ r i22 ^V 2 2 n ( ^r i ) + к ⁽¹³⁾ Подставляя формулу (13) в формулу (7) и пренебрегая поверхностными слагаемыми, а также деформациями кручения и продольного изгиба (определяемыми взаимодействиями молекул в соседних смектических слоях), получаем в духе работ [2, 3] следующую энергию деформации в расчете на одну молекулу системы:

^ F _l,_l = 1 K ii ( divn ) 2 , (14) где константа упругости поперечного изгиба может быть записана в следующем виде:

K 11 = y ⁷ 0 S 2 J J 202 ^{( r} 12 ) ^r 12 ^dr 12 • ⁽¹⁵⁾ 2₀

На рис. 2 представлена конфигурация двух молекул, в которой межмолекулярный вектор r 12 лежит в одной плоскости ZY с главными молекулярными осями a 1 и a 2 и направлен вдоль оси Y. В такой конфигурации деформация поперечного изгиба полностью описывается двумя углами α ₁ и α 2 , а ориентации векторов a 1 , a 2 , и u 12 могут быть выражены следующим образом:

u ₁₂ = { 0, 1, 0 } , a 1 = { 0, - sin o 1 ,cos a 1 } , a ₂ = { 0,sin a ₂,cos a ₂ } .

Будем для простоты считать a 1 = a ₂ = a /2 . Тогда из формул (4), (7), (14), (15) легко получить:

1 то                                  1 то

K 11 ~ О 0 S 2 J J 202 ⁽ r 12 ) r 12 d r 12 ~ ^О 0 S 2 f

Тем самым, оценивая потенциал для двух реальных молекул в положении бок-о-бок, вычисляя вторую производную от него по углу α и интегрируя эту производную по расстоянию между молекулами согласно формуле (17), можно оценить константу упругости поперечного изгиба для всего смектического материала.

Деформации кручения и продольного изгиба ( K ₂₂ и K ₃₃) и спонтанное закручивание k ₂

Сопротивление деформациям кручения и продольного изгиба в смектическом состоянии определяется взаимодействием соседних смектических слоев. Формула (11) описывает энергию упругости

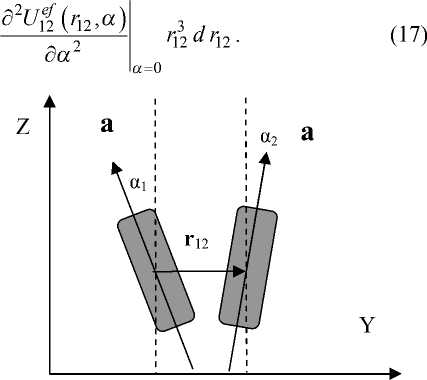
Рис. 2. Две взаимодействующие молекулы в смектическом слое с длинными осями, лежащими в одной плоскости.

синклинного смектического состояния по отноше- нию к этим типам деформаций. Запишем градиентное разложение для директора нематического порядка, подразумевая, что изменение директора от слоя к слою мало:

ⁿ i + 1 = ⁿ i ⁺ h ( k ^-V ) ⁿ i ^{+ 1} h ² ( ^k -V ) ² n i + K                           (18)

Используя формулу (18) и пренебрегая поверхностными слагаемыми и деформацией поперечного изгиба (определяемой взаимодействиями молекул внутри одного смектического слоя), получаем следующие выражения для приращений Δ T ℓLλ ( n i , k , n i+1 ) ≡ T ℓLλ ( n i , k , n i+1 ) – T ℓLλ ( n i , k , n i ):

^A T 000 ⁽ n i , ^k , n i + 1 ) = 0,

A T 202 ( n i , k , n i + 1 ) = - 1 h ² { ( n - rotn ) ² + [ n x rotn ] ² } ,

A T 220 ^{( n} i , k , ⁿ i + 1 ) = ^A T 022 ^{( n} i , ^k , ⁿ i + 1 ) = °,

^A T 212 ( n i , k , n i + 1 ) = ^{- h} ( n ^{- rotn} ) ,

A T₂₂₂ ( n i , k , n i + 1 ) = - ₂ h ² { - ( n - rotn ) 2 + ₂ [ n x rotn ] ²

Тем самым, из формулы (11) можно извлечь следующую энергию деформации в расчете на одну молекулу системы:

^{A F}i - 1,i ^{+ A F}i,i + 1 = I K 22 ( ^{n - rotn} ) ^{2 +} 2 K 33 [ n ^{x rotn} ] ^{2 +} k 2 ( n ^{- rotn} ) ,              ⁽²⁰⁾

где константы упругости кручения и продольного изгиба, а также псевдоскаляр спонтанного кручения могут быть записаны в следующем виде:

**     **   *

K 22 ~ ^{3 h} ( J 202 ^- J 222 ) , K 33 ~ ^{3 h} ( J 202 ⁺ ₂ J222 ) , k 2 ~ ^h J 212 ,

где коэффициенты J^*_ℓLλ есть коэффициенты аппроксимации потенциала взаимодействия молекул в соседних смектических слоях [см. формулу (9)]. Предположим, что директор нематического порядка n i испытывает небольшое азимутальное вращение Δ φ от слоя к слою. Принимая во внимание формулу (19) и рассматривая только слагаемые, зависящие от Δ φ , можем переписать выражение (20) в следующем виде:

AF i - 1,i +AF_t ■

—1V K ₂ sin⁴ 9 cos² A® 19T K 3 sin² ( 29 ) cos Am -¹ k ₂ sin² 9 sin Am . (22) 2 h ²²²2 h ²³³ h ²

Формула (22) дает принципиальную возможность оценить коэффициенты K ₂₂, K ₃₃ и спонтанное закручивание k 2 для реальных молекул жидкого кристалла следующим образом. Допустим, что мы узнали геометрию молекул и можем рассчитать потенциал их взаимодействия. Тогда, распо ложив молекулы, как показано на рис. 3, мы можем построить зависимость реального потенциала Серия «Математика, физика, химия», выпуск 11 ₄₁

от азимутальной разницы Δ φ и аппроксимировать полученную зависимость формулой (21), откуда автоматически получаем коэффициенты K 22 , K 33 и спонтанное закручивание k 2 . Равновесный угол геликоидального вращения Δ φ может быть получен минимизацией свободной энергии (21):

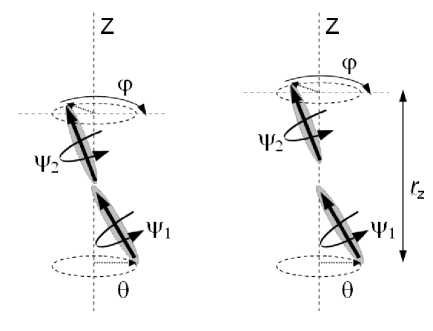
Рис. 3. Взаимное расположение молекул в соседних смектических слоях, используемое для аппроксимации потенциала формулой (22)

Аф » hk 2 j22 sin²9 + K33 cos²9), (23) а шаг спирали (число смектических слоев в одном периоде) равен 2π/Δφ.

Заключение

В рамках молекулярно-статистического подхода были получены выражения констант упругости поперечного изгиба, кручения и продольного изгиба (K11, K22, и K33) и выражение для шага спирали для наклонной смектической фазы. Предло- жен метод оценки всех перечисленных парамет ров эффективного взаимодействия для реальных веществ на основе оценки взаимодействия пары молекул в выбранных конфигурациях. Предварительно геометрия молекул может быть рассчитана стандартными квантово-химическими методами (например, в программе PC GAMESS, разработанной профессором МГУ А.А. Грановским). Данные о взаимодействиях атомных групп, участвующих в молекулярном строении, могут быть взяты из таблиц.

Работа выполнена при поддержке гранта РФФИ 08-03-90009 и гранта Миннауки MK-2004.2008.2.