Методика расчета магнитной восприимчивости пленок железо-иттриевого граната с линейным дефектом структуры типа прямой сквозной трещины во внешнем магнитном поле
Автор: Судоргин Сергей Александрович, Лебедев Николай Геннадьевич, Иванченко Геннадий Сергеевич, Игнатьев Вячеслав Константинович
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Физика
Статья в выпуске: 1 (32), 2016 года.
Бесплатный доступ
Предложена методика расчета магнитной восприимчивости пленок железо-иттриевого граната с линейными дефектами структуры типа прямой сквозной трещины. Проведены численные расчеты пленок железо-иттриевого граната без дефектов структуры, с линейными дефектами структуры в виде прямой сквозной трещины различной ширины и с различным положением относительно края пленки. Для исследования магнетизма коллективизированных электронов в пленках железо-иттриевого граната используется модель Хаббарда, которая описывает движение электронов на решетке и их локальное кулоновское взаимодействие, когда электроны оказываются на одном узле.
Железо-иттриевый гранат, динамическая магнитная восприимчивость, модель хаббарда, дефекты структуры, внешнее магнитное поле
Короткий адрес: https://sciup.org/14969008
IDR: 14969008 | УДК: 537.636 | DOI: 10.15688/jvolsu1.2016.1.6
Текст научной статьи Методика расчета магнитной восприимчивости пленок железо-иттриевого граната с линейным дефектом структуры типа прямой сквозной трещины во внешнем магнитном поле
DOI:
В последнее десятилетие развитие методов напыления сверхтонких пленок и нанолитографии привело к активному изучению магнитных наноструктур и открытию новых физических явлений: эффекта гигантского магнитосопротивления, туннелирования магнитного момента в сверхмалых ферромагнитных частицах, высокотемпературного ферромагнетизма. Разрабатываются новые магнитные наноматериалы с уникальными характеристиками, которые планируется в будущем применять для сверхплотной записи и хранения информации, при создании новых датчиков магнитного поля, а также для разработки элементной базы квантовых компьютеров. Кроме того, изучение магнитных характеристик низкоразмерных наноструктур является одной из наиболее актуальных фундаментальных задач физики конденсированного состояния вещества [2; 11].
Помимо теоретического интереса актуальной практической задачей является обнаружение и оценка местонахождения и геометрических параметров дефектов сплошности, которые необходимо выявлять для диагностики технического состояния изделий. Для решения этой задачи необходимо рассчитывать поля рассеяния для разного типа нарушений сплошности с учетом их геометрических размеров, магнитных свойств материала и конфигурации изделия, в котором находится дефект. В данной работе акцент сделан на исследовании влияния наноразмерных дефектов в пленочных структурах ферромагнитных материалов [3; 6].
Модель Хаббарда для неоднородной ферромагнитной пленки
Железо-иттриевый гранат (ЖИГ) является одним из ферромагнитных материалов, имеющих широкие перспективы практического применения. ЖИГ используется в микроволновых и магнитооптических устройствах, например, в ЖИГ-резонаторах, перестраиваемых генераторах и фильтрах СВЧ-диапазона, широкополосных умножителях частоты [3; 8; 11]. В общем случае гранаты – минералы, относящиеся к силикатам, с общим типом химической формулы R32 + R 3 +( SiO 4 ) 3, где R2+ - атомы Mg, Fe, Mn Ca; R3+ - атомы Al, Fe, Cr, обладающие сложной кристаллической структурой [9]. Железо-иттриевый гранат имеет химическую формулу вида Y3Fe2(FeO4)3, и представляет собой красно-бурые кристаллы. Ионы железа Fe3+ занимают октаи тетраэдрические позиции в соотношении 2 : 3 и формируют две магнитные подрешетки с противоположно направленными спинами. Температура Нееля равна примерно 555 K [16].
Для практического применения наиболее важны ЖИГ в виде монокристаллов и эпитаксиальных пленок. В последние годы исследуется также ЖИГ в наноструктурном состоянии [5; 12; 14; 15]. Интерес к наноструктурным материалам на основе ЖИГ обусловлен как фундаментальными вопросами физики нанокристаллических магнетиков, так и перспективами их использования в покрытиях, нанокомпозитах, феррожидкостях и пр. [4].
Наиболее широко применимой моделью для исследования магнетизма коллективизированных электронов является модель Хаббарда [13], которая описывает движение электронов на решетке и их локальное кулоновское взаимодействие, когда они оказываются на одном узле. Гамильтониан модели в терминах вторичного квантования имеет вид:
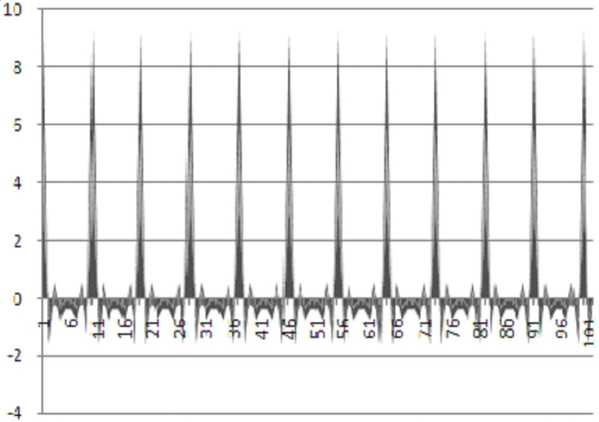
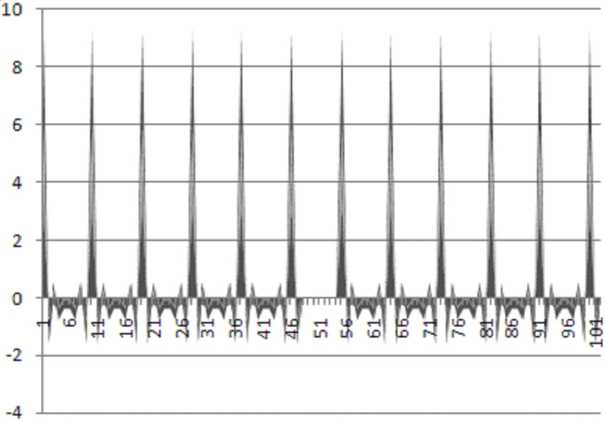
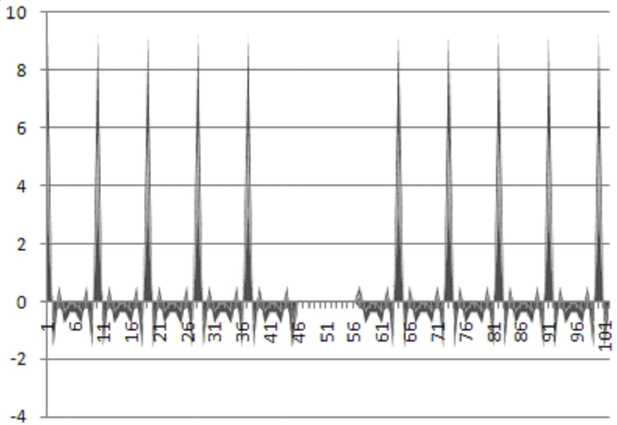
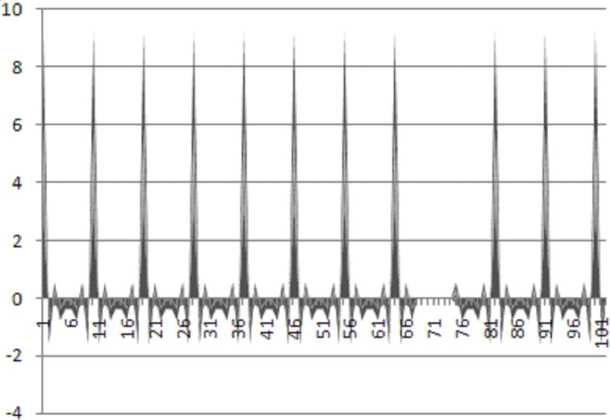
H = y tu ij io jo о io 11 t ф/ tjσ iσ В гамильтониане (1) электронные состояния не вырождены, поэтому два электрона могут оказаться на одном узле, если их спины противоположны. Здесь cо и cо+ - ферми-операторы уничтожения и рождения электрона на узле i со спином о, который принимает два значения: Т и Ф, niо= cо+ciо- число электронов со спином о на узле i, ео- атомный электронный уровень, tij – матричный элемент перескока электрона с узла на узел. Обычно предполагают, что последний отличен от нуля только для ближайших соседей. Модель Хаббарда является частным случаем полярной модели Вонсовского, в которой наряду с кулоновским взаимодействием на одном узле учитывается взаимодействие электронов на соседних узлах. Диагональность того или иного члена в гамильтониане дает возможность построения теории возмущений в двух предельных случаях: U<< W и U >> W, которые называются пределами слабой и сильной связи соответственно. Используем приближение сильной связи, так как пленки ЖИГ являются ферромагнитным материалом. В пределе U<< W система представляет собой ферми-жидкость, в которой возможно возникновение магнитного дальнего порядка: ферромагнитного (F) или типа волны спиновой плотности (SDW) с волновым вектором Q. Это – режим коллективизированного магнетизма без локализованных магнитных моментов. Оператор кинетической энергии диагонализуется при помощи фурье-преобразования электронных операторов: 1 ikR, + 1 V - ikR, + c = У e ic. , c. = —;= У e ic. (2) iσ kσ iσ kσ . Nk Nk где N – число узлов в кристалле. Динамическая магнитная восприимчивость в приближении хаотических фаз определяется выражением [13]: x(k,”)= l X0(kft ) ,(3) 1 - Ux (k, to) о/, \ 1 f E(k))- f (e(k, -k)) _« Z 4 где X (k,ю) = — У, / —г—/ ‘«затравочная» восприимчивость свободных (зонных) элект- ' ' N1J к(k, - k)-к(k,)+ to + i5 ронов; f (e) =---7----------7фермиевская функция распределения, EF - энергия уровня Ферми. exp((e - Ef)/T) +1 Приближенно кристаллическую решетку ЖИГ можно считать кубической [1], зонная структура для ЖИГ пленки имеет вид: e(k,, ky )= t (cos (k,a) + cos (kya)),(4) где t = 1.7 эВ – интеграл перескока между соседними узлами решетки кристалла; a = 1,2376 нм – параметр кристаллической решетки ЖИГ. Рассмотрим пленку ЖИГ с линейным дефектом – трещиной, параллельной границам пленки, как показано на рисунке 1. Здесь обозначено: xd – координата расположения дефекта, 2d – ширина линейного дефекта Рис. 1. Пленка ЖИГ с линейным дефектом, параллельным оси y Для учета дефекта дисперсионное соотношение запишем в виде системы уравнений: e (kx, k,H t(cos(kxa) + cos(kya)) 0 < x< xd - d, 0, xd - d < x < xd + d, t (cos (kxa) + cos (ky a)) xd + d< x< Lx, где xd – координата дефекта по оси х; 2d – ширина дефекта; Lx – ширина пленки (по оси х); Ly – длина пленки 2n ,2 (по оси y). Значения волновых чисел находятся в диапазоне -----< kx< — при 0 < x< xd - d; xd - da 2п ,2л 2л, 2п, ---------< k < — при xd + d < x < L ; — < k < — при 0 < y < L . Волновые числа k и k могут при-Lx - xd - d x a d x Ly ' a yx y нимать дискретные разрешенные значения: ky 2n n Ly, 7 12n n e Z, ky < —. y a; kx = , n e Z, kx< — при 0 < x< xd - d; xd - da , 2n n2 kx =-----------, n e Z, kx< при xd + d< x< Lx. Lx — xd — da Используя приближение хаотических фаз (ПХФ), находим выражение для продольной динамической магнитной восприимчивости: 2X||(k, ®) = Xi(k, ®)= X^kTT . 1 - UX (k, to) Зависимость продольной динамической магнитной восприимчивости от координат можно получить, применяя преобразование Фурье к х|| (k, to): 71 71 1 1 3a 3a Х||(г,T) = —jX||(k,to)elkrdk = — J |X||(kx,ky,toyrdkxdky. (7) 2П 2П 0 0 Намагниченность во внешнем магнитном поле выражается формулой: M ||(r, T ^X^r, T)H 0, (8) где H0 – напряженность внешнего магнитного поля. Для численного моделирования было выбрано значение напряженности внешнего магнитного поля H0 = 1 Тл. Результаты численного моделирования На рисунке 2 представлено распределение продольной магнитной восприимчивости для ЖИГ пленки без дефектов. Геометрические размеры пленки: по координате x – 100 усл. ед., по координате y – 10 усл. ед. Величина одной условной единицы равна 1 усл. ед. = 1,2376 нм. Рис. 2. Распределение продольной магнитной восприимчивости для ЖИГ пленки без дефектов На рисунке 3 представлено распределение продольной магнитной восприимчивости для ЖИГ пленки с линейным дефектом шириной 6 усл. ед., расположенным на расстоянии 50 усл. ед. от края пленки. Рис. 3. Распределение продольной магнитной восприимчивости для ЖИГ пленки с линейным дефектом шириной 6 усл. ед., расположенным на расстоянии 50 усл. ед. от края пленки На рисунке 4 представлено распределение продольной магнитной восприимчивости для ЖИГ пленки с линейным дефектом шириной 10 усл. ед., расположенным на расстоянии 50 усл. ед. от края пленки. Рис. 4. Распределение продольной магнитной восприимчивости для ЖИГ пленки с линейным дефектом шириной 10 усл. ед., расположенным на расстоянии 50 усл. ед. от края пленки На рисунке 5 представлено распределение продольной магнитной восприимчивости для ЖИГ пленки с линейным дефектом шириной 6 усл. ед., расположенным на расстоянии 70 усл. ед. от края пленки. Рис. 5. Распределение продольной магнитной восприимчивости для ЖИГ пленки с линейным дефектом шириной 6 усл. ед., расположенным на расстоянии 70 усл. ед. от края пленки Заключение Разработана методика для расчета поля рассеяния и его характеристик линейных нанораз-мерных дефектов в ферромагнитных пленках. Создана программа, вычисляющая продольную и поперечную динамическую магнитную восприимчивость тонких квазиодномерных пленок, содержащих линейные дефекты. Рассчитаны распределения магнитной восприимчивости в ЖИГ пленках с дефектом в виде трещины. Распределения магнитной восприимчивости проанализированы для ЖИГ пленок без дефектов, для пленок с дефектами различной ширины. Произведено моделирование для различного пространственного расположения линейных дефектов в ЖИГ плен- ках. Изучено влияние геометрических размеров ферромагнитных пленок на их магнитную восприимчивость, которая позволяет рассчитать характеристики поля рассеяния.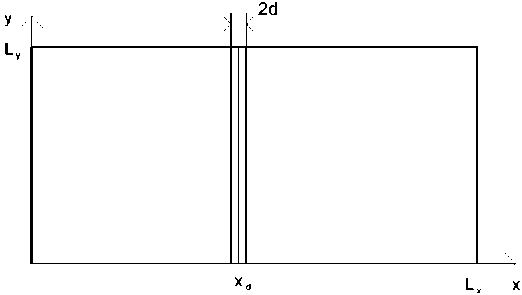
Список литературы Методика расчета магнитной восприимчивости пленок железо-иттриевого граната с линейным дефектом структуры типа прямой сквозной трещины во внешнем магнитном поле
- Бондаренко, Г. Г. Термостабилизация двух частот спектра магнитостатической спиновой волны в пленке кубического феррита/Г. Г. Бондаренко, В. В. Шагаев//Известия высших учебных заведений. Физика. -2011. -№ 1/2. -C. 85-90.
- Загидулин, Р. В. Расчет магнитостатического поля внутреннего дефекта и дефекта внутренней поверхности в ферромагнитной пластине. 1. Магнитное поле дефекта внутри ферромагнетика/Р. В. Загидулин, В. Ф. Мужицкий, В. П. Курозаев//Дефектоскопия. -1997. -№ 1. -С. 46-54.
- Коржова, Л. В. Теоретические и экспериментальные исследования магнитостатических полей дефектов/Л. В. Коржова//Физические методы и средства неразрушающего контроля. -Минск: Наука и техника, 1976. -С. 74-92.
- Оптические и магнитооптические свойства наноструктурного железо-иттриевого граната/Б. А. Гижевский, Ю. П. Сухоруков, Е. А. Ганьшина //ФТТ. -2009. -№ 51. -C. 1729-1734.
- Паняев, И. С. Техника измерений спектральных и материальных параметров тонких пленок ЖИГ/И. С. Паняев, Д. Г. Санников//Известия Самарского научного центра Российской академии наук. -2012. -№ 14. -С. 1092-1095.
- Печенков, А. Н. Алгоритмы расчетов и моделирования прямых и обратных задач магнитостатической дефектоскопии и устройств технической магнитостатики: дис. д-ра техн. наук/Печенков Александр Николаевич. -Екатеринбург, 2007. -271 с.
- Рандошкин, В. В. Прикладная магнитооптика/В. В. Рандошкин, А. Я. Червоненкис. -М.: Энергоатомиздат, 1990. -320 с.
- Сазонов, Д. М. Перестраиваемые ферритовые фильтры. Антенны и устройства СВЧ/Д. М. Сазонов. -М.: Высш. шк., 1988. -434 с.
- Смит, Я. Ферриты/Я. Смит, Х. Вейн. -М.: Иностр. лит., 1962. -504 с.
- Структура и свойства напыленых пленок железо-иттриевого граната/В. Ф. Шкарь, Е. И. Николаев, В. Н. Саяпин //ФТТ. -2005. -№ 47. -C. 1071-1074.
- Тикадзуми, С. Физика ферромагнетизма. Магнитные свойства вещества/С. Тикадзуми. -М.: Мир, 1983. -302 с.
- Anisotropic hyperfine field fluctuation in La Pb Mn Fe O/H. M. Lee, S. J. Kim, I. B. Shim, S. B. Kim, 0.67 0.33 1-x x 3 C. S. Kim//J. Magn. Magn. Mater. -2004. -№ 272. -P. 1764-1766.
- Hubbard, J. Electron correlations in narrow energy bands/J. Hubbard//Proc. Roy. Soc. A. -1963. -№ 276. -P. 238-257.
- Phase and microstructure evolution in precursor plasma-sprayed YIG coatings/X. Z. Guo, B. G. Ravi, Q. Y. Yan //Ceramics International. -2006. -№ 32. -P. 61-66.
- Particle size effects on magnetic garnets prepared by a properties of yttrium iron sol-gel method/R. D. Sanchez, J. Rivas, P. Vaqueiro, M. A. Lopez-Quintela, D. Caeiro//J. Magn. Magn. Mater. -2002. -№ 247. -P. 92-98.
- Wood, D. L. Effect of Impurities on the Optical Properties of Yttrium Iron Garnet/D. L. Wood, J. P. Remeika//J. Appl. Phys. -1967. -№ 247. -P. 92-98.


