Методика расчета плавного перехода между двумя круглыми экранированными волноводами, основанная на интегральном соотношении Лоренца

В настоящее время в технической электродинамике актуальными являются задачи по расчету и оптимизации параметров согласующих устройств волноводного тракта. Строгое решение такого рода задач может быть осуществлено, например, с использованием распространенных в технической электродинамике метода частичных областей (МЧО), метода минимальных автономных блоков (ММАБ) [1–4], метода поперечных сечений [5]. У данных методов имеются несомненные достоинства: математическая обоснованность, хорошее соответствие теоретических и экспериментальных результатов, физичность математических моделей. Однако, использование МЧО и ММАБ сопряжено со сложностью алгоритмизации дифракционных задач. Использование метода поперечных сечений ограничивается, как правило, требованием медленности изменения параметров профиля продольного сечения нерегулярного участка волновода.

Одним из универсальных методов решения сложных внутренних дифракционных задач электродинамики является метод интегральных уравнений, основанный на лемме Лоренца. В данной работе предлагается общий подход к расчету передаточных характеристик перехода, имеющего заданный профиль продольного се- чения. Расчет проведен методом интегральных уравнений, основанным на соотношении Лоренца, предложенным в [6–10].

Целью решения данной задачи является по- строение алгоритма расчета характеристик передачи плавного перехода, соединяющего волноводы круглого поперечного сечения различных радиусов. Данный алгоритм может быть использован для расчета переходов в принципе любых профилей.

1. Постановка задачи об осесимметричном сочленении двух волноводов

Исследуемая структура изображена на рис. 1.

Область рассматриваемой волноведущей структуры представляет собой объем, ограниченный поверхностями S1, S2 и S3, в котором существуют электромагнитные поля E1 и Й 1; E2 и Й2, соз-^ 2, m   ^ 2, m данные соответственно источниками j1 и j2 . Здесь S1, S2 и S3 – боковые поверхности волноводов I и II, соответственно.

Согласно лемме Лоренца эти поля связаны соотношением:

^([EiН2]-[E2Hi]) dS =

S

П ^. ► ^. ► ^. ► ^. ► j,E 2 - j₂E 1 - j 1 H 2 + j₂ H 1 ) dV ,

V

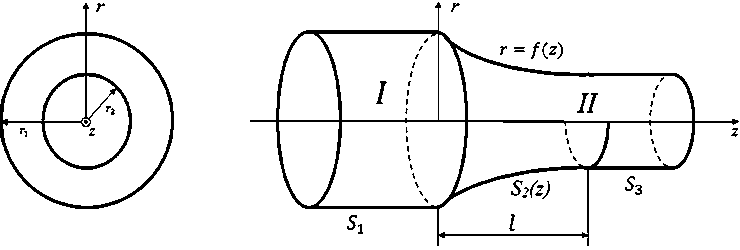
Рис. 1. Плавный переход между экранированными волноводами круглого сечения

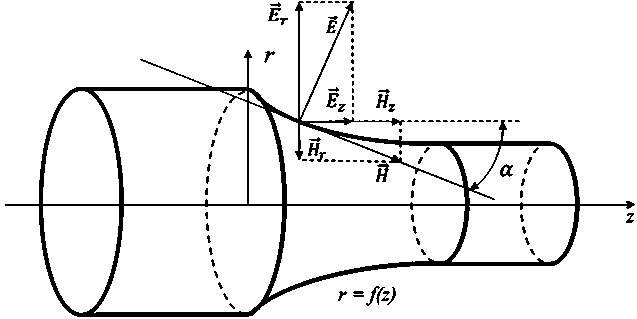
Рис. 2. Взаимное расположение компонент электромагнитного поля на поверхности r = f ( z )

где E _b Й 1 — поля, переносящие в рассматриваемом сочленении энергию, эти поля удовлетворяют уравнениям Максвелла и граничным условиям:

E т / ₈ = 0, Й п / ₈ = 0;                                  (2)

S – экранирующая поверхность направляющей структуры. Эти поля создаются реальными ис- e,    - e, m точниками j1 , j2   – вспомогательные источ ники, создающие поля E2 и Й2 (эти источники располагаются вблизи стыка). Поля Й2 удовлетворяют нулевому граничному условию, когда z ^ м.

Далее следуем методике, предложенной в работах [6–10].

В силу граничных условий (2) уравнение (1) можно переписать в следующем виде:

j [ Hi Е2 ] ds =

^S                                                     (3)

= j ( - е - - EE- - - т н2 + - mH ) dv.

V

В неограниченном пространстве источники jy , создадут поле сферической волны E q , Й q . В этом случае уравнение (1) запишется как: -   »     -   »     -     »     -     »

j ( jEE 2 - j₂Е q - jyH 2 + j₂H q ) dV = 0.       (4)

V „

Располагая источники j₂ ’ вблизи стыка z = 0, удаляя S y 2 в м , вычитая из уравнения (3) уравнение (4), получаем:

j [ H i Е2 ] ds =

^S                                                     (5)

• - e -       -      - m -       -

• = j (j 2 (E q - E1) - j 2 (H q - H1) dV.

V

При выводе уравнения (5) учтена тождественность интегрирования по бесконечному объему V _M и по объему источников V .

Выбираем в качестве вспомогательных источников элементарные электрические и магнитные диполи:

• - e , m ^- e , m ^{-  -} e , m

j 1,2 = I2 5(T - Tj 1,2), где T и rem — соответственно координаты точек наблюдения и точек источников. Воспользовавшись свойством 5- функций, из (5) получаем:

.   .        .    -      .-

H1Е2]dS = 12 H 1(rj2)(7)

S

– для случая, когда вспомогательное поле создается магнитным диполем;

j [ H1Е2 ]ds = --2E1(-e 2)(8)

S

– для случая, когда вспомогательное поле создается электрическим диполем.

В выражениях (6)–(8) I^{e , m} – амплитуды вспо- - e , m могательных источников j .

Решая интегральные уравнения (7), (8) при граничных условиях (2), определяем искомые поля E и H - 1 в нерегулярной линии передач. При этом отсутствуют ограничения на вид аналитических функций, описывающих продольный профиль экранирующей поверхности.

Рассмотрим структуру, изображенную на рис. 1. На область сочленения двух экранированных волноводов круглого поперечного сечения из z ^ —м со стороны волновода i (радиус 7 1 ) падает одна из собственных волн этого волновода. В результате дифракции этой волны на границе с областью II в волноводе I возбуждается бесконечный набор отраженных волн с коэффициентами отражения R_n^E_q (для E -волн) и R_n^H_q (для H -волн), а в волноводе II образуется бесконечный набор прошедших волн с коэффициентами прохождения B_n^E_q (для E -волн) и B_n^H_q (для H -волн).

Продольные составляющие электрического и магнитного полей в областях I и II записывают- ся в виде [4]:

Ezi (7, ф) = (anq ) 3n (anqi7) Фn (ф) х м          2

х exp (— jРnqiz) + ^^ Rnq (аnq ) х n, q=0

х 3n (anqi7) Ф n (ф) exp (jPnqiz) , Hzi (7, ф) = (anq ) 3n (anqi7) Фn (ф) х

H         hH  E ²

х exp ( jPnqiz) + t^ Rnq (anq ) х

n , q = 0

х 3n (anqi7) Ф n (ф) exp (jPnqiz) ,

Ez,i (7,ф)= £ Bn, (aEqf х n, q=0

х 3n (anqii7) Фn (ф) exp (—jPnqiiz) ,

HzII (7, ф)= £ Bnq (aHq )2 х n, q=0

х 3n (anqii7) Фn (ф) exp (—jPnqiiz) ,

где

E    hnq    E a nqi        ; a nqii

H _ nqnq      H a nqi    7 ’    a nqii

h nq f(z), h'

nq

.

f ( z )

В вышеприведенных выражениях имеют место следующие обозначения: anq, aHq — попереч- ные волновые числа Е- и Н-волн круглого волновода соответственно; f(z) – функция, определяющая зависимости компонент электромагнитного поля на поверхности перехода от координаты z, то есть определяющая профиль поверхности области II (в дальнейшем функция профиля);

Вид зависимости поля от азимутальной координаты выражен функциями: '

Фn (ф) = sin (nф) и Фn (ф) = cos (nф), n = 0,1,2, _

Отметим, что f ( z ) – является кусочно-заданной функцией:

f ( z ) =

f0(z ),    0 <  z <  l ;

72,    z > l, s — абсолютная диэлектрическая проницаемость среды; Л — абсолютная магнитная проницаемость среды; Рnq, РHHq — постоянные распространения Е- и Н-волн круглого волновода соответственно; hnq, hnq — корни функции Бесселя и производной от данной функции, соответственно.

Отметим, что связь волновых чисел выглядит следующим образом:

s^2 —(anqH )2 = (e nqH )2.

Пользуясь известными соотношениями [4], компоненты исследуемого поля в регулярном волноводе i и в области волновода ii ( l <  z < м )

выражаются через продольные составляющие электромагнитного поля (9).

Далее получим связь компонент полей для Е -и Н -волн на поверхности волновода ii (0 <  z <  l ). Это поверхность нерегулярного волновода, поперечное сечение которого определяет функция профиля f ( z ). Поверхность данного волновода определяется как 7 = f ( z ).

Так как в уравнениях (7) и (8) рассматривается поле на поверхности волновода ii (0 < z < l), необходимо получить связь компонент полей, а именно выразить компоненты полей Н- и Е-волн через компоненты Ez и Hz на поверхностях это- го волновода.

Рассмотрим рис. 2. Из него видно, что

E₇ = | e| cos a , где tg ( a ) — тангенс угла наклона касательной к поверхности 7 = f ( z ). При этом *

E_z = E sin a , откуда E₇ = E z / f '( z ).

Аналогично получаем следующее выражение H₇ = H_zf '( z ). Таким образом, на поверхности 7 = f ( z ) получили следующую связь компонент полей:

E z

E           ,

При выборе места расположения вспомогательных источников были рассмотрены рекомендации, представленные в работе [12]. В данной работе рассмотрен расчет характеристик передачи перехода двух круглых экранированных волноводов методом, основанным на интегральном соотношении Лоренца. Отметим, что решение интегрального уравнения является инвариантным по отношению к месту расположения вспомогательных источников.

По предлагаемому алгоритму был проведен расчет характеристик передачи исследуемого перехода: зависимости модулей коэффициентов отражения и прохождения распространяющихся волн от нормированной частоты.

Данные зависимости были получены для основной волны H₁₁ круглых волноводов с соотношением размеров Г 2 / г = 0.6, L / г = 1. Функция профиля плавного перехода в данном случае имеет линейную зависимость от z : fo ( z ) = ( r - r j z / L + r .. Зависимости получены в приближении N = 7, когда в волноводах I и II учитывается первые 7 волн Н- и Е-типа по порядку следования критических частот, и представлены на рис. 4, б .

При решении системы уравнений в том или ином приближении при конечном числе точек, в которые помещаются вспомогательные источники, их координаты можно выбирать произ- вольным образом. Оптимальное же их расположение определяется из условия минимизации погрешности выполнения закона сохранения энергии (ЗСЭ). В общем случае закон сохранения энергии записывается в виде:

^\Rnq H^,E2 + ^\B nq ^H,E² = 1,             (26)

n , q                  n , q

H,E H,E где Rnq и Bnq нормированные коэффициенты отражения и прохождения распространяющихся H и E волн в исследуемой структуре.

Эти коэффициенты вычисляются по формулам:

H,E ^{P H} nq ^,E nq      H,E

I R nq     \= ~ I R nq     I,

P _{H 11}

P

где PH E – мощность распространяющейся nq, nq                   HE      HE волны с коэффициентами RnqH,E и BnqH,E; PH – мощность падающей волны на нерегулярный участок тракта (в нашем случае H11).

Погрешность выполнения закона сохранения энергии вычисляется по формуле:

A= ^ \ R nq ^H,E 2

!nq ^H,E \ ² — 1 ■ 100%.

При решении дифракционной задачи поле на стыке двух волноводов, представлялось в виде набора прошедших и отраженных Н- и Е-волн (в случае возбуждения стыка H11-волной). При этом в формуле (26) учитывались коэффициен-

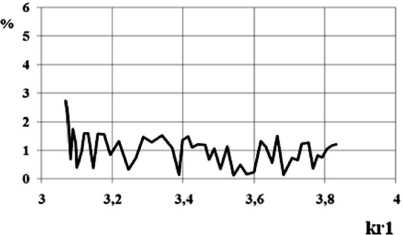
Рис. 5. Зависимость погрешности при проверке выполнения закона сохранения энергии для волны H₁₁ от нормированной частоты

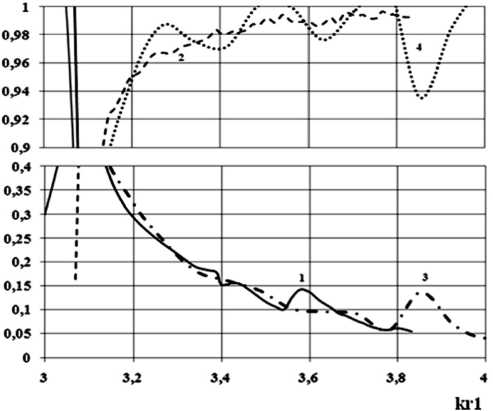
Рис. 6. Зависимости модулей коэффициентов отражения – 1 и прохождения – 2 (решение задачи методом леммы Лоренца), отражения – 3 и прохождения – 4 (расчет САПР СВЧ CST Studio Suite), волны H11 от нормированной частоты ты отражения и прохождения всех распространяющихся волн волноводов I и II.

На рис. 5 представлена зависимость относительной погрешности А выполнения закона сохранения энергии для волны H₁₁ от нормированной частоты для линейного профиля перехода с соотношениями размеров Г 2 / г = 0.6, L / г = 1.

Как следует из представленного графика, погрешность выполнения ЗСЭ в среднем по диапазону частот не превышает 2 ^, имеются определенные выбросы на графике (до 3 ^) вблизи критических частот волн высших типов, распространяющихся в стыкуемых волноводах.

С целью проверки корректности полученных результатов были рассчитаны характеристики передачи плавного перехода, имеющего линейный профиль продольного сечения, между двумя экранированными волноводами круглого поперечного сечения с соотношением размеров r / r i = 0.6, L / r i = 1 с помощью средства автоматического проектирования CST Studio Suite. Результаты расчетов изображены на рис. 6 со-

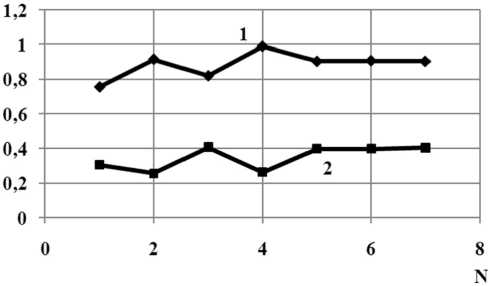
Рис. 7. Зависимости модулей коэффициентов отражения – 1 и прохождения – 2, волны H₁₁ от номера приближения N для значения kr = 3.07537

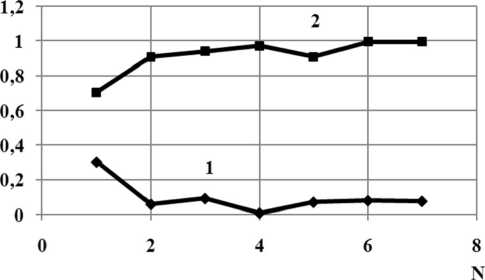
Рис. 8. Зависимости модулей коэффициентов прохождения – 1 и отражения – 2, волны H₁₁ от номера приближения N для значения kr = 3.70708

вместно с результатами, проиллюстрированными на рис 4, б .

Сравнение результатов, представленных на рис. 6 показывает, что имеет место хорошее качественное и количественное совпадение результатов, полученных на основе разработанного алгоритма, с результатами, рассчитанными с использованием системы автоматического проектирования СВЧ CST Studio Suite.

Также для оценки корректности разработанного алгоритма и полученных результатов была исследована сходимость решения дифракционной задачи. Результаты исследований для линейного профиля плавного перехода между двумя экранированными волноводами с соотношением размеров r / г = 0.6, L / г = 1 изображены на рис. 7 и 8.

Анализ результатов, представленных на рис. 7 и 8 показывает, что при учете 7 собственных волн (7 приближение) в сочленяемых волноводах при решении дифракционной задачи наблюдается стабильность в зависимости от приближения в значениях передаточных характеристик перехода. Дальнейшее увеличение номера приближения приводит к увеличению порядка СЛАУ, при незначительном изменении

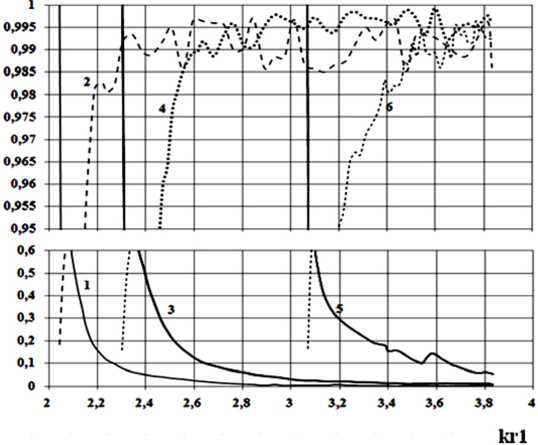
Рис. 9. Зависимости модулей коэффициента отражения – 1 и прохождения – 2 ( r ₂/ r ₁ = 0.9), отражения – 3 и прохождения – 4 ( r ₂/ r ₁ = 0.8), отражения – 5 и прохождения – 6 ( r ₂/ r ₁ = 0.6) волны H₁₁ от нормированной частоты

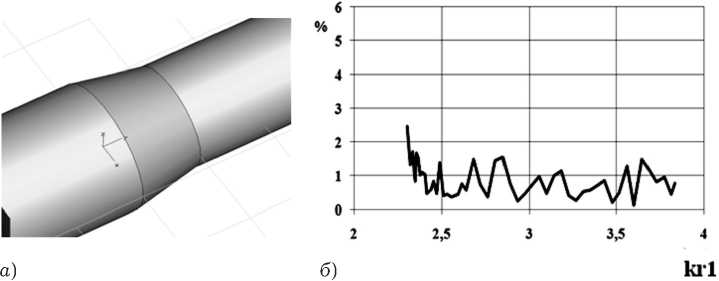
Рис. 10. Внешний вид исследуемой структуры ( а ); б ) зависимость относительной погрешности выполнения закона сохранения энергии для волны H₁₁ от нормированной частоты для размеров r ₂/ r ₁ = 0.8, L / r ₁ = 1

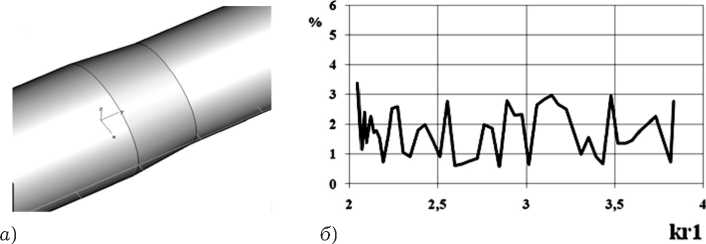
Рис. 11. Внешний вид исследуемой структуры ( а ); б ) зависимость относительной погрешности выполнения закона сохранения энергии для волны H₁₁ от нормированной частоты для размеров r ₂/ r ₁ = 0.9, L / r ₁ = 1

• ( ~ 0.5 %) значений передаточных характеристик. Данный анализ дает возможность выбрать «рабочее» приближение N = 7 для расчета перехода.

Для проверки устойчивости работы алгоритма решения дифракционной задачи были рассчитаны характеристики передачи плавного перехода для основной волны H₁₁ круглого волновода, с соотношением сторон r ₂/ r ₁ = 0.9, L / r ₁ = 1 и для плавного перехода с параметрами r ₂/ r ₁ = 0.8, L / r ₁ = 1, в обоих случаях плавный переход имеет линейный профиль продольного сечения.

Эти зависимости получены в конечном приближении N = 7 и изображены на рис. 9 совместно с результатами, представленными на рис. 4, б .

Анализ результатов, представленных на рис. 9, показывает, что с увеличением отношения радиусов поперечного сечения стыкуемых волноводов, соединенных переходом линейного профиля, наблюдается ухудшение характеристик передачи перехода в рабочем диапазоне частот. Данный результат достаточно хорошо иллюстрирует физические представления о со-

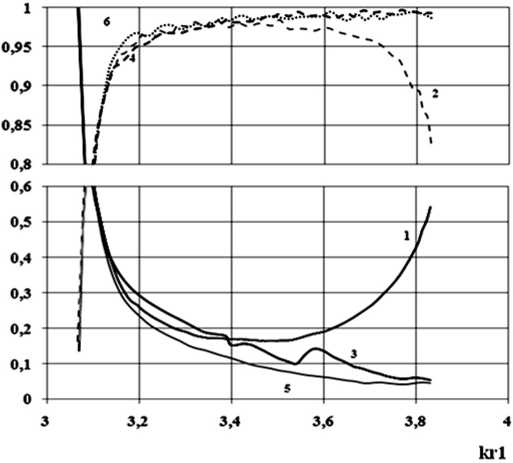
Рис. 12. Зависимости модулей коэффициента отражения – 1 и прохождения – 2 ( r ₂/ r ₁ = 0.6, L = 0.3 r ₁), отражения – 3 и прохождения – 4 ( r ₂/ r ₁ = 0.6, L = r ₁), отражения – 5 и прохождения – 6 ( r ₂/ r ₁ = 0.6, L = 1.5 r ₁) волны H₁₁ от нормированной частоты

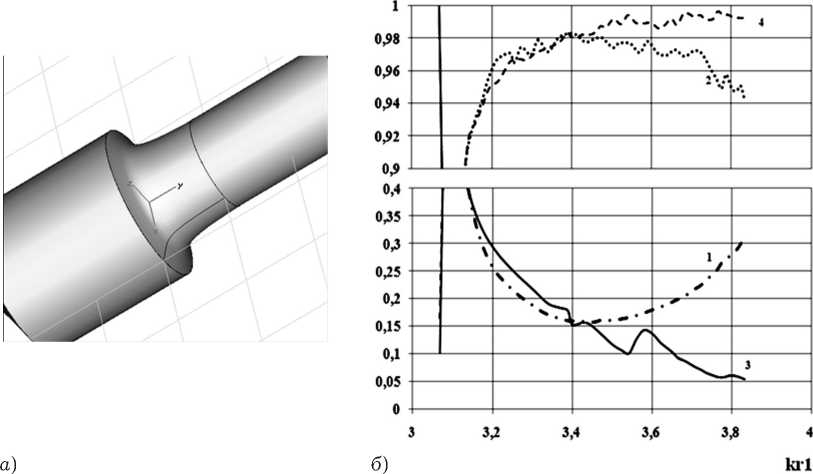
Рис. 13. Внешний вид исследуемой структуры ( а ); б ) зависимости модулей коэффициента отражения – 1 и коэффициента прохождения – 2 (гиперболический профиль), коэффициента отражения – 3 и коэффициента прохождения – 4 (линейный профиль) волны H₁₁ от нормированной частоты

гласовании различных направляющих систем. Отметим, что относительная погрешность выполнения ЗСЭ при расчете плавного перехода линейного профиля с соотношением размеров r ₂/ r ₁ = 0.9, r ₂/ r ₁ = 0.8, L / r ₁ = 1 во всем диапазоне частот работы перехода в среднем составляет 2.5 ^ (рис. 10, 11).

Для оценки физичности полученных результатов рассмотрим поведение характеристик передачи в зависимости от изменения длины участка плавного перехода. Данные характеристики были получены для значений длины перехода

L = 0.3 r ₁, L = r ₁, L = 1.5 r ₁, для линейного профиля, в конечном приближении N = 7, и изображены на рис. 12.

Анализ результатов, представленных на рис. 12 показал, что с ростом длины перехода происходит улучшение согласования данного устройства в рабочем диапазоне частот. Отметим, что увеличение длины перехода в то же время приводит к уменьшению массо-габаритных показателей устройства согласования.

Для исследования возможностей разработанного алгоритма были рассчитаны передаточные

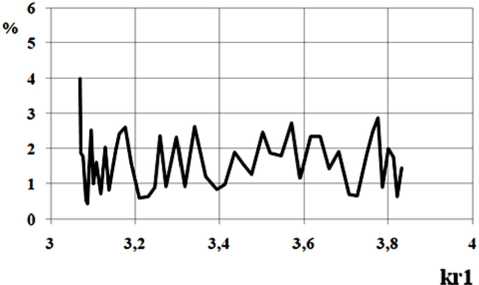
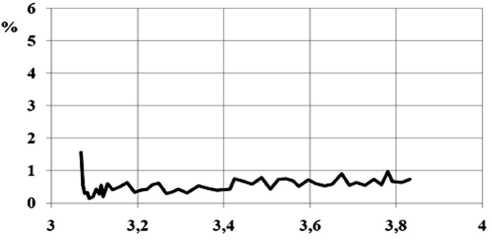
Рис. 14. Зависимость погрешности выполнения закона сохранения энергии для волны H₁₁ от нормированной частоты

характеристики плавных переходов с различными профилями: гиперболическим, экспоненциальным и косинусоидальным.

Рассмотрим результаты исследования характеристик передачи плавного перехода с гиперболическим профилем:

fo ( ² ) = ( ⁴ ^Х Zt • z (Г2 - Г 1 ) + Lr

Данные зависимости были получены для основной волны H₁₁ круглого волновода с геометрическими параметрами 7 2 / r = 0.6, L / r = 1, в конечном приближении N = 7, и представлены на рис. 13, б , относительная погрешность выполнения ЗСЭ – на рис. 14. Для сравнения на рис. 13, б приведены характеристики передачи перехода с линейным профилем с теми же геометрическими размерами стыкуемых волноводов.

Из рис. 13, б видно, что значение коэффициента отражения плавного перехода с гипер- болическим профилем продольного сечения во всем исследуемом диапазоне частот выше, чем у перехода с линейным профилем, а, следовательно, такой переход менее согласованный.

На основе разработанного алгоритма были рассчитаны характеристики передачи плавного перехода с экспоненциальным профилем:

f 0 ( ² ) =

1 - exp( - L ) r - 7 2

( exp( - z ) - 1 ) + 7 1 .

Зависимости получены для возбуждения перехода основной волной H₁₁ прямоугольного волновода с соотношением радиусов 7 2 / 7 1 = 0.6, L / 7 1 = 1, в приближении N = 7, и представлены на рис. 15, б совместно с результатами, проиллюстрированными на рис. 4, б , относительная погрешность выполнения ЗСЭ – на рис. 16.

Необходимо отметить (рис. 15, б ), что значение коэффициента отражения плавного перехода с экспоненциальным профилем продольного сечения в первой половине исследуемого диапазона частот выше по сравнению с переходом линейного профиля, то есть такой переход менее согласованный в данном частотном диапазоне. Однако, во второй половине частотной области экпоненциальный переход является более согласованным. Очевидно, что для уменьшения значения модуля коэффициента отражения волны H₁₁ в исследуемом диапазоне частот необходимо увеличить длину перехода с экспоненциальным профилем, что в свою очередь ухудшит массогабаритные показатели исследуемого перехода.

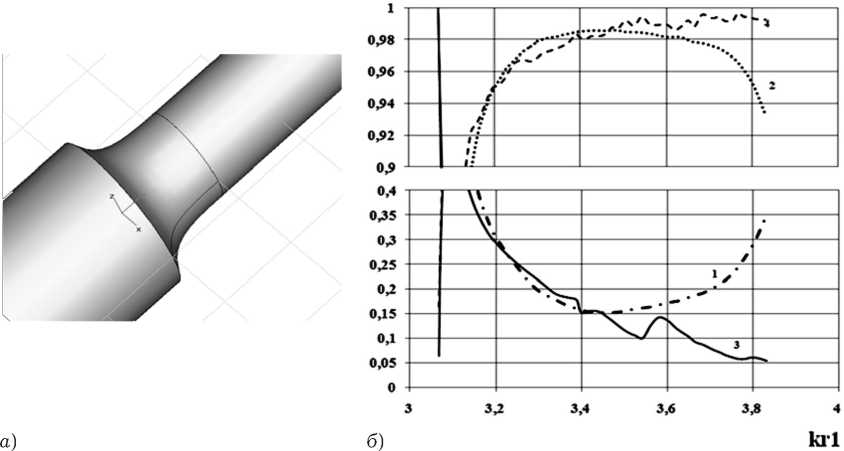
Рис. 15. Внешний вид исследуемой структуры ( а ); б ) зависимости модулей коэффициента отражения – 1 и коэффициента прохождения – 2 (линейный профиль), отражения – 3 и коэффициента прохождения – 4 (экспоненциальный профиль) волны H₁₁ от нормированной частоты

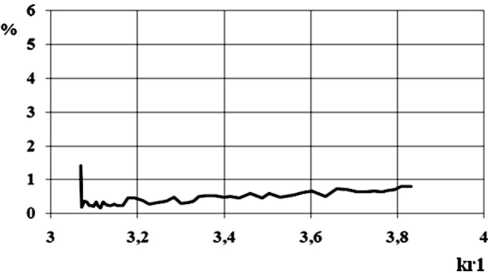
Рис. 16. Зависимость относительной погрешности выполнения закона сохранения энергии для волны H₁₁ от нормированной частоты перехода с экспоненциальном профилем для соотношения размеров r 2 / г = 0.6, L / r i = 1

Отметим, что относительная погрешность выполнения ЗСЭ при расчете перехода с экспоненциальным профилем продольного сечения в среднем по частотному диапазону составляет менее 1 ^ (рис. 16).

Результаты расчета характеристик передачи перехода с косинусоидальным профилем

Г - Г    (П Z) Г + Г f (Z ) = —---1cos + —---1.

0 ^V ’      2        ( L )      2

представлены на рис. 17, б, а зависимость относительной погрешности выполнения ЗСЭ от нормированной частоты – на рис. 18. Представленные зависимости были получены при возбуждении перехода основной волной H11 волновода круглого поперечного сечения с соотношением радиусов r2 / Г = 0.6, L / ri = 1, в приближении N = 7. В целях сравнения совместно с данными результатами на рис. 17, б показаны характеристики передачи перехода, имеющего линейный профиль, полученные при тех же геометрических параметрах сочленяемых волноводов.

Качественное сравнение характеристик передачи плавных переходов с косинусоидальным и линейным профилями продольного сечения, представленных на рис. 17, б , показывает явное преимущество первого при использовании его в качестве согласующего элемента в исследуемом диапазоне частот.

Анализ представленных на рис. 18 результатов показал, что в среднем по диапазону значение относительной погрешности составляет менее 1 ^.

С целью проверки корректности полученных результатов были рассчитаны характеристики передачи плавного перехода, имеющего косинусоидальный профиль продольного сечения, между двумя круглыми экранированными волноводами с геометрическими параметрами r 2 / r i = 0.6, L / r i = 1 с помощью средства автоматического проектирования CST Studio Suite. Результаты расчетов изображены на рис. 19 совместно с характеристиками передачи, полученными на основе предлагаемого метода, проиллюстрированными ранее на рис. 17, б .

Сравнение результатов решения задачи предлагаемым методом с результатами, полученными при помощи САПР СВЧ (рис. 19), дает хорошее количественное и качественное их совпадение в исследуемом диапазоне частот.

Для дополнительной оценки корректности полученных результатов была исследована сходимость решения дифракционной задачи для плав-

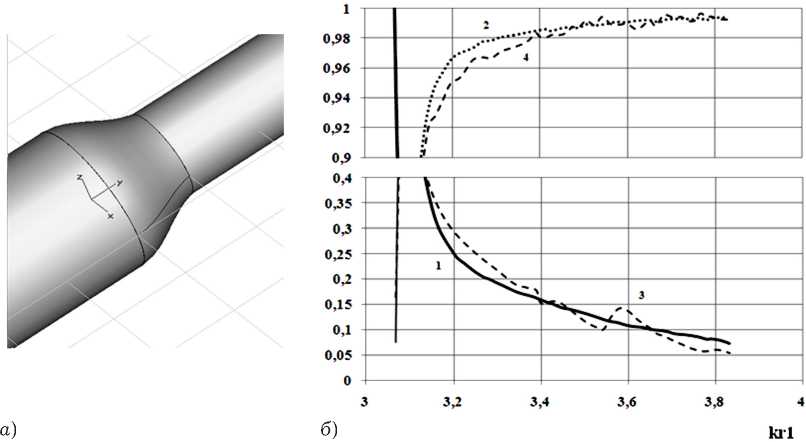
Рис. 17. Внешний вид исследуемой структуры ( а ); б ) зависимости модулей коэффициента отражения – 1 и коэффициента прохождения – 2 (косинусоидальный профиль), отражения – 3 и коэффициента прохождения – 4 (линейный профиль) волны H₁₁ от нормированной частоты

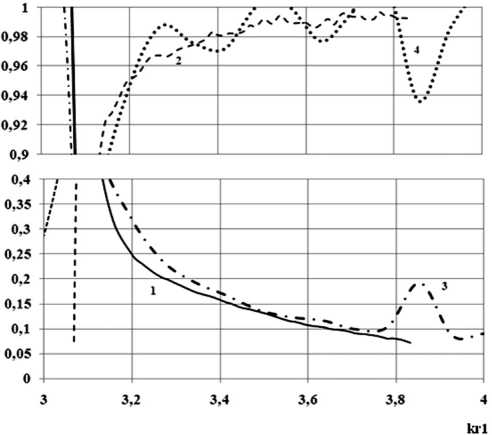
Рис. 19. Зависимости модулей коэффициентов отражения – 1 и прохождения – 2 (решение задачи методом леммы Лоренца), отражения – 3 и прохождения – 4 (расчет САПР СВЧ CST Studio Suite), волны H₁₁ от нормированной частоты

kil

Рис. 18. Зависимость погрешности выполнения закона сохранения энергии для волны H₁₁ от нормированной частоты перехода с косинусоидальным профилем для соотношения размеров r ₂/ r ₁ = 0.6, L / r ₁ = 1

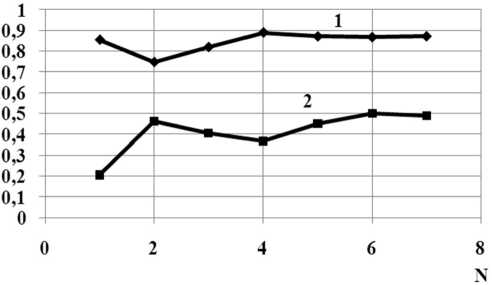
Рис. 20. Зависимости модулей коэффициентов отражения – 1 и прохождения – 2, волны H₁₁ от номера приближения N для значения kr ₁ = 3.07537

ного перехода, имеющего косинусоидальный профиль продольного сечения с соотношением размеров стыкуемых волноводов r ₂/ r ₁ = 0.6, L / r ₁ = 1. Результаты исследований изображены на рис. 20 и 21.

Анализ графиков сходимости решения дифракционной задачи, изображенных на рис. 20 и 21 показал, что при расчете передаточных характеристик перехода с косинусоидальным профилем продольного сечения необходимо учитывать по 7 собственных волн в стыкуемых волноводах (рабочее приближение N = 7).

На рис. 22 представлены характеристики передачи плавного перехода косинусоидального профиля для основной волны H₁₁ круглого волновода. Переходы имели следующие геометрические параметры: r ₂/ r ₁ = 0.9, L / r ₁ = 1 (кривые 1 и 2), r ₂/ r ₁ = 0.8, L / r ₁ = 1 (кривые 3 и 4), r ₂/ r ₁ = 0.6, L / r ₁ = 1, (кривые 5 и 6). Из рисунка следует,

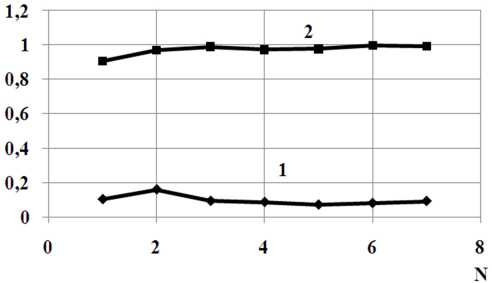
Рис. 21. Зависимости модулей коэффициентов отражения – 1 и прохождения – 2, волны H₁₁ от номера приближения N для значения kr ₁ = 3.70708

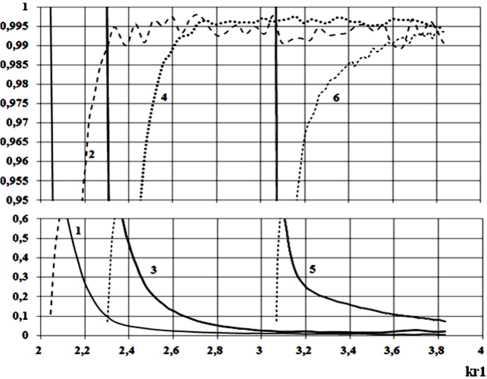
Рис. 22. Зависимости модулей коэффициента отражения – 1 и прохождения – 2 (r2/ r1= 0.9), отражения – 3 и прохождения – 4 (r2/ r1= 0.8), отражения – 5 и прохождения – 6 (r2/r1= 0.6) волны H11 от нормированной частоты что с увеличением перепада размеров поперечных сечений стыкуемых волноводов, соединенных переходом косинусоидального профиля, происходит ухудшение согласования перехода. Аналогичный результат был получен при исследовании перехода линейного профиля. Номер приближения при расчете характеристик, изображенных на рис. 22, N = 7.

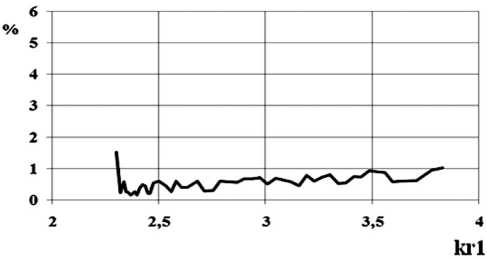
Рис. 23. Зависимость относительной погрешности выполнения закона сохранения энергии для волны H₁₁ от нормированной частоты для размеров стыкуемых волноводов Г 2 / r i = 0.8, L / r i = 1, профиль — косинусоидальный

Как следует из представленного графика, изображенного на рис. 23, при расчете передаточных характеристик перехода косинусоидального профиля с соотношениями размеров r 2 / r i = 0.8, L I Г = 1, относительная погрешность выполнения ЗСЭ для волны H₁₁ в рабочем диапазоне частот в среднем менее 1 ^.

Из графика, изображенного на рис. 24, следует, что при расчете передаточных характеристик перехода косинусоидального профиля с соотношениями размеров r 2 / г = 0.9, L / г = 1, относительная погрешность выполнения ЗСЭ для волны H₁₁ в рабочем диапазоне частот в среднем составляет 1.5^.

Таким образом, на основании предложенной методики и разработанного алгоритма был проведен расчет передаточных характеристик плавных переходов различного профиля продольного сечения, соединяющих круглые волноводы разных поперечных сечений. С целью проверки универсальности алгоритма были рассчитаны передаточные характеристики переходов разных профилей продольного сечения для различных соотношений геометрических параметров стыкуемых волноводов. Проведено сравнение получаемых с помощью предложенного метода результатов с результатами, получаемыми с использованием лицензионного пакета прикладных программ САПР СВЧ CST Studio Suite. Пр е дложенный метод обеспечивает высокое быстродействие и дает наглядное представление о внутренних физических процессах.

Представленные расчеты показали, что из четырех рассмотренных функций профиля (линейного, косинусоидального, гиперболического и экспоненциального), наилучшие передаточные характеристики обеспечивает в одинаковых частотных диапазонах при одинаковой длине перехода переход с косинусоидальной функцией профиля

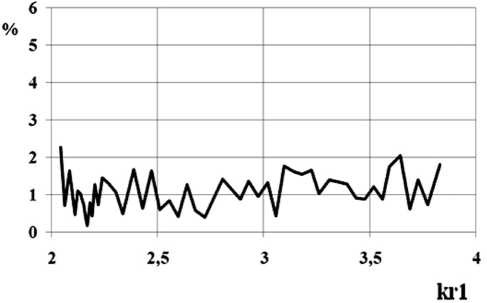
Рис. 24. Зависимость относительной погрешности выполнения закона сохранения энергии для волны H₁₁ от нормированной частоты для размеров стыкуемых волноводов Г 2 / r i = 0.9, L / r i = i, профиль — косинусоидальный

Г - Г    ( П Z) Г + Гf (Z ) = —---^ cos + —---^ .

• ^{0 V 7}      2        ( L )     2

что указывает на эффективность использования предлагаемого метода в задачах оптимизации и параметрического синтеза. Необходимо отметить, что представленный алгоритм расчета передаточных характеристик плавного перехода, соединяющего направляющие структуры различного поперечного сечения, является универсальным и применим для решения задач дифракции электромагнитных волн на нерегулярных участках различных волноведущих структур.

Данный алгоритм даже в малом приближении может быть использован для расчета передаточных характеристик различных конфигураций продольного сечения переходов между двумя волноводами.