Методика расчета системы охлаждения электрических двигателей в составе трансмиссии колесной машины

В настоящее время электротрансмиссии получают все большее распространение в силу своих очевидных преимуществ по бесступенчатости регулирования скорости и момента, а также широких возможностей по автоматизации регулирования и оптимизации совместной работы с ДВС [1]. Кроме того, интерес к электрическим трансмиссиям усиливается по мере разработки все более компактных и энергонасыщенных электромашин и силовых преобразователей [2].

В частности, фирма «Магнет мотор» (ФРГ) установила электрическую трансмиссию на гусеничную боевую машину пехоты «Мардер» с 440 кВт ДВС при мощности двух бортовых электродвигателей (ЭД) по 750 кВт каждый. В начале 90-х годов фирмой выпущена многоколесная машина с формулой 8×8 полной длиной 7 м, шириной 3 м, массой 32 т, ДВС мощностью 600 кВт, с восьмью ЭД мощностью по 70–80 кВт каждый, установленными непосредственно в колесах [3].

В РФ также ведутся работы по внедрению электрических трансмиссий для транспортных средств большой мощности. Потери энергии, а следовательно, и нагрев увеличивается пропорционально с увеличением нагрузки. Поэтому наибольшая мощность нагрузки, допускаемая для данной машины, определяется главным образом допустимым уровнем нагревания, а также механической прочности ее частей.

Одна из проблем, возникших при этом – утилизация выделяющегося тепла. Дело в том, что преобразование энергии в электромашинах неизбежно связано с ее потерями, вызванными перемагничиванием ферримагнитных сердечников, преобразованием тока через проводники, трением в подшипниках и о воздух. Электромашины являются достаточно совершенными преобразователями энергии с относительно высоким КПД. Например, в самых мощных электрических машинах КПД равен 98–99,5 %, а в машинах мощностью 10 кВт – 50–70 %. Подобные величины КПД при столь малых мощностях в других машинах невозможны [4].

Теряемая в электромашинах энергия превращается в тепло и вызывает нагревание отдельных ее частей. Для надежности работы и достижения приемлемого срока службы нагревание частей машины должно быть ограничено. Наиболее чувствительными к нагреву являются электроизоляционные материалы, качество которых определяет допустимый уровень нагрева электрических машин. Большое значение имеет способ отвода тепла и охлаждения.

Охлаждение электрических машин бывает воздушным и жидкостным. При воздушном охлаждении поток воздуха, нагнетаемый вентилятором, обтекая нагретые поверхности, уносит часть тепла, тем самым, поддерживая температуру частей электрической машины на приемлемом уровне. В случае жидкостного охлаждения отвод избыточного тепла осуществляется жидкостью, циркулирующей в рубашке охлаждения. Существуют различные конфигурации контуров жидкостного охлаждения электрических машин. Самый простой и основной – это полость с охлаждающей жидкостью вокруг статора электромашины. В этом случае жидкость подводится и отводится с разных сторон статора и тепло, генерированное электрической машиной, принимает охлаждающая жидкость. Различные системы непосредственного охлаждения во всех случаях выполняются замкнутыми с циркуляцией одной и той же массы охлаждающего агента с охлаждением его в специальных охладителях. При непосредственном охлаждении обмоток перепады температуры в изоляции исключаются и можно резко увеличить плотность тока. При водяном охлаждении мощность машины ограничивается в основном уже не условиями нагрева, а другими техническими и экономическими показателями.

Расход охлаждающей среды (м3/с), необходимый для отвода тепла, по классической мето-p дике [5] равен: V = , где p – отводимые потери, Вт; с – удельная объемная теплоемкость c⋅ΘВ охлаждающей среды, Дж/(град·м3); ΘВ=ΘГ-ΘХ – перепад температур нагретой охлаждающей среды и поступающей в машину, °С. Для воды с = 3,85·106 Дж/(град·м3). Величина ΘВ в зависимости от способа циркуляции жидкости изменяется в пределах 12–30 °С.

В связи с появлением мощных компьютеров методы расчета теплонапряженности различных систем стали активно развиваться. Для определения локальных гидродинамических параметров течения жидкости с учетом турбулентности и вихревого характера потока в полости в последние годы все чаще используют численные методы на основе CFD (Computational Fluid Dynamics) моделей, в частности, метод конечных элементов, реализуемый с помощью CAE (Competraided engineering) технологий [6].

В специализированной CAD (Computer – aided design) программе создается объемная модель полости охлаждения. В качестве начальных условий принимается расход на входе в полость системы охлаждения статора и отвода нагретой жидкости. Результаты расчета методом конечных элементов представлены в виде полей векторов скоростей течения жидкости вдоль поверхностей охлаждения цилиндра. При этом каждый вектор соответствует определенному значению скорости. В ходе данного исследования был проведен расчетный анализ системы охлаждения статора электромашины. Расчет произведен в приложении ANSYS CFX [6].

Рассмотрены два контура охлаждения статора (рис. 1 и 4). Для обоих вариантов расчета принято: расход охлаждающей жидкости G = 0,8 кг/с; температура охлаждающей жидкости на входе в рубашку охлаждения статора t = 30 °C; мощность электромашины P = 100 КВт.

Схема рубашки охлаждения варианта № 1 представлена на рис. 1. Данная конфигурация являет собой распространенный вариант решения задачи по охлаждению электромашины. Он недорог, прост в изготовлении и эффективен. Рассмотрим его в качестве основного варианта и определим его параметры. Подача охлаждающей жидкости осуществляется через левый патрубок, отвод – через правый.

Рис. 1. Схема рубашки охлаждения статора электромашины

Результаты гидравлического расчета представлены на рис. 2: установлено распределение потоков жидкости внутри полости охлаждения, определены зоны с малой и большой скоростью течения жидкости. Максимальная скорость жидкости 3,35 м/с (в точках входа и выхода), минимальная 1,16·10 ^–2 м/с. Результаты теплового расчета представлены на рис. 3.

Рис. 2. Иллюстрация движения жидкости в полости охлаждения

Рис. 3. Иллюстрация результатов теплового расчета рубашки охлаждения

По результатам расчета видно, что перепад температуры относительно входа и выхода в рубашке охлаждения составляет 17 °С. Это связано с тем, что скорости жидкости различных точках рубашки охлаждения существенно отличаются, имеются зоны с «нулевой» скоростью и как следствие этого – низкий теплоотвод от статора. Кроме того, на рисунках видны зоны перегрева и зоны, где жидкость практически не меняет свою температуру.

Вариант № 2: рубашка охлаждения (рис. 4) представляет собой спиральный канал, в котором охлаждающая жидкость не имеет возможности произвольно менять свое направление и скорость внутри объема, как это имеет место в варианте № 1. И как следствие, результаты расчета имеют существенные отличия.

Результаты гидравлического расчета представлены на рис. 5. В данном примере скорость жидкости по всей траектории движения составляет 3,32 м/с. И только в местах подвода и отвода имеют место незначительное изменение скорости, что не оказывает влияние на теплообменные процессы. В данной схеме движения жидкости не наблюдаются места, где жидкость имеет скорость близкой к нулю. И перепад по скоростям входа и выхода меньше, чем в первом варианте, он составляет всего 0,89 м/с.

Рис. 4. Схема рубашки охлаждения статора электромашины со спиральным каналом

Рис. 5. Иллюстрация движения жидкости в полости охлаждения

По результатам теплового расчета (рис. 6) видно, что в отличие от первого варианта, где перепад температуры относительно входа и выхода в рубашку охлаждения составляет 17 °С, в данном варианте почти столько же – 18 °С. Но, при этом, максимальная температура жидкости в первом варианте 78 °С, а во втором – всего 48 °С и жидкость в контуре нагревается равномерно, и нет зон перегрева.

Аналогично выше изложенному набору начальных условий (расход охлаждающей жидкости G = 0,8 кг/с; температура охлаждающей жидкости на входе в рубашку охлаждения статора t = 30 °C) проведены расчеты при различных расходах охлаждающей жидкости через рубашку охлаждения и получены зависимости между разностью температур в контуре охлаждения электромашины и расходом. Результаты расчетов приведены на рис. 7. Сюда же помещен график (3) ΔΤ(G), построенный по классической методике. Анализ графиков показывает, что существующая методика оценки теплонапряженности в системе охлаждения электродвигателя в целом соответствует результатам моделирования процесса в пакете программ ANSYS CFX, о чем свидетельствует расположение графика (3) между (1) и (2). Но, с другой стороны, не позволяет оценить их с большой точностью: например при одном и том же расходе охлаждающей жидкости в 1 кг/с перепад температур ΔΤ по классической методике, которая не учитывает особенности потока жидкости в рубашке охлаждения, составляет 20 °С, при потоке жидкости без организации спирального канала составляет 41 °С, а при организации спирального канала всего 14 °С.

Temperature Contour 1

П 3.210e+002 3.200e+002 3.190e+002 3.180e+002 3.170e+002 3.161e+002 3.1516+002 3.141 e+002 3.1316+002 3.121e+002 3.1116+002 3.1016+002 3.0916+002 3.0816+002 3.0716+002 3.0616+002 ^ 3.051 e+002 ■ 3.0416+002 ■ 3.0316+002

Рис. 6. Иллюстрация результатов теплового расчета рубашки охлаждения

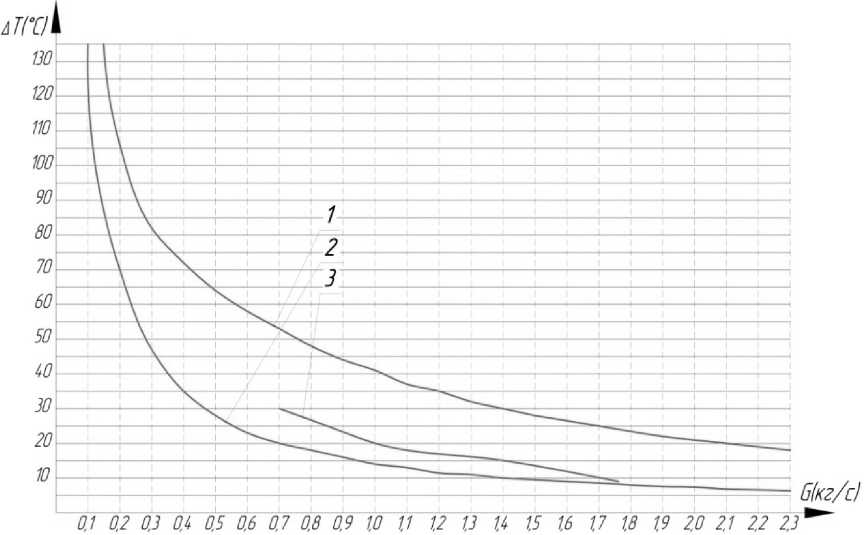
Рис. 7. Результаты исследований: 1 и 2 – первый и второй варианты при различных расходах охлаждающей жидкости через них; 3 – значения параметров, рассчитанных по формуле из [4]

Можно сказать, что внедрение в инженерную практику современных средств математической имитации реальных физических процессов, в данном случае теплообмена, позволяет ввести в классическую методику уточняющий коэффициент К , величина которого составляет 14 41

20 ... 20 = 0,7...2,05 , и существенно уточнить результаты расчетов, что, в свою очередь, позво- лит более обоснованно подходить к назначению конструктивных параметров рубашки охлажде- ния электродвигателей.

Выводы

• 1.    Предложена методика расчета тепловой напряженности системы охлаждения электрических двигателей в трансмиссии колесной машины с организацией различных направлений потоков охлаждающей жидкости на основе апробированных пакетов программ ANSYS CFX, уточняющая существующую классическую методику.

• 2.    Проведено сравнение диаграмм ΔΤ (G), рассчитанных по классической методике и с помощью пакета программ ANSYS CFX для различных вариантов организации потока охлаждающей жидкости в рубашке охлаждения. Получен уточняющий коэффициент К = 0,7...2,05 , отражающий специфику потока жидкости, которую не учитывает классическая методика.

• 3.    Обоснован наилучший вариант (спиралевидный контур) по организации потока в рубашке, обеспечивающий равномерное охлаждение и минимальные локальные температуры и перепады между входом и выходом не превышающие 10–15 °С.

• 4.    Установлено, что для вентильных двигателей мощностью 100 кВт оптимальный расход охлаждающей жидкости находится в пределах от 0,9 до 1,3 м ³ /с при условии организации движения охлаждающей жидкости в контуре охлаждения по типу второго варианта.

• 5.    Разработанная методика может быть использована и для других вариантов организации потоков охлаждающей жидкости и применена для оценки теплообмена в электрической трансмиссии колесной машины.