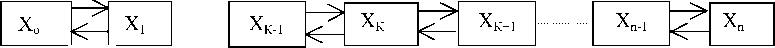Методика развертывания и поддержания орбитальных группировок космических систем информационного обеспечения

• -    количество орбитальных плоскостей и размещение восходящих узлов орбит в плоскости экватора;

• -    количество космических аппаратов (КА) в орбитальной группировке, их распределение по плоскостям, размещение внутри плоскости и взаимное фазирование между КА в соседних плоскостях;

• -    параметры орбиты КА.

Тип и свойства орбитальной группировки (ОГ) КСИО определяют номенклатуру применяемых средств выведения и стратегию их использования.

Для многоплоскостных ОГ с несколькими КА в каждой плоскости возникает необходимость взаимной расстановки КА в плоскости и поддержание взаимной конфигурации на весь период функционирования КА. Этот тип ОГ относится к сетевым ОГ с корректируемыми орбитами. Для сетевых ОГ экономически оправдано использование групповых схем выведения КА, особенно на этапе развертывания ОГ.

Для многоплоскостных ОГ с одним КА в каждой плоскости применяются одиночные схемы выведения.

Восполнение КА в ОГ может быть осуществлено с использованием следующих критериев:

• -    после полного отказа КА;

• -    по прогнозу появления полного отказа КА;

• -    по истечению гарантийного срока;

• -    из-за экономической или технической нецелесообразности дальнейшей эксплуатации.

Использование двух первых критериев приводит к необходимости построения вероятностной модели существования ОГ. Два остальных приводят к возможности применения детерминированной модели существования ОГ.

Орбитальная группировка КСИО в варианте однотипных КА имеет три фазы существования: развертывание, поддержание и деградация.

В случае модернизации ОГ темпы обновления подбираются таким образом, чтобы суммарное количество КА в ОГ сохранялось постоянным (деградация старых КА компенсируется развертыванием новых КА).

Методика развертывания и поддержания ОГ с детерминированной схемой восполнения. Состояние ОГ из однотипных КА на этапе развертывания моделируется следующей системой уравнений:

• а)    длительность развертывания ОГ ( t ^ ) от начального состава N ”™ до номинального состава N 0 _Г :

t ^ =А t В • ( N £ - N- ) ;           (1)

• б)    текущее количество КА в ОГ ( N ог ) на этапе развертывания:

нз нз

N ог =     =     - N О г , A t q - N - <  t ^:<  t ,     (2)

^{A t} В ^t раз

, нз нз ог ог I д/"нач         нз / Л/Р VHa4

AtP AtP + N ог ’ 0 < tог

Уравнения (1), (2) справедливы при отсутствии неудачных запусков и отсутствии отказов вновь вводимых КА на интервале развертывания ОГ.

Поддержание номинального количества КА в ОГ (NO'-р) обеспечивается выбором темпа запуска (A tВТ), при котором за tВТ обновится вся ОГ (N0_г):

1 №

П _ .КА / ОТ⁰ 1  —__¹ ог

^AtВ ^tFc / N ог , Ав п КА ^,         W

AtВ    tгс где Ав - интенсивность восполнения; tКА - гарантийный срок активного существования КА.

Количество КА в ОГ для выбранного темпа запусков будет не менее NO_гпри отсутствии неудачных запусков и отсутствии отказов КА в пределах tКА . Прекращение запусков после достижения штатного состояния ОГ приводит к ее деградации, которое моделируется следующим уравнением:

пз

N^Т = № - ^tог

N ог N ог   . П ’                   ⁽ ^

A tВ где tПг - текущее время с момента прекращения запусков (tПг < tКА ); N0г - текущее количество КА в ОГ (при условии отсутствия отказов КА в пределах tКА ).

В процессе модернизации ОГ, когда осуществлена замена одной модели КА на другую, темп развертывания ОГ с новой моделью КА выбирается равным темпу запусков старой модели КА при поддержании ОГ.

Методика развертывания и поддержания ОГ при случайном процессе ее восполнения. В формализованном виде состояние ОГ (X(t) - текущее количество КА в ОГ) описывается в виде дискретного марковского случайного процесса (процесса «гибели» и «размножения»), в котором множество состояний X(t) ставится в однознач

ное соответствие с рядом целых неотрицательных чисел К= 0,1,..., п. Причем соседние состояния отличаются на ±1 (кроме крайних значений).

Граф состояние процесса гибели и размножения при

При достаточно большом математическом ожидании (т = %/ц > 20) закон распределения сечения случайной функции Х'(/) можно приближенно считать нормальным.

Доверительная область значения величины вероятности текущего количества КА в ОГ X(t) = Nо_гопределяется выражением [4]

веден на рисунке.

Все вероятностные характеристики процессов «гибели» и «размножения» зависят только от следующих параметров [1; 2]:

• -    количества состояний 0 < К < п + 1;

• -    интенсивности потока восполнения % ;

  - интенсивности потока отказов Ц_к. ‘

При этом интенсивности потоков % , Ц являются математическими ожиданиями некоторых случайных функций, т. е. в общем случае являются неотрицательными, неслучайными функциями времени t [2].

Рассмотрим несколько вариантов модельного описания состояния ОГ.

Модель 1. Показатели интенсивности постоянны: %_к = %_В, Ц_к = к • ц_от. Отсутствуют ограничения на количество состояний (п ^ ^).

При этом интенсивность потока событий %_В - интенсивность запуска КА на орбиту, интенсивность потока событий Ц_от - интенсивность полных отказов КА, а состо-яниеХ состоит в том, что в момент времени t работоспособны К единиц КА. Рассмотрим случайную величи-нуХ^) - число КА в ОГ в момент времени t и найдем ее характеристики.

Математическое ожидание числа КА в ОГ mxp₁ = M[^(^)] и дисперсия D [X(t)] = D^1 в момент времени t при развертывании ОГ описывается следующим выражением [2]:

limBm {t Ф1 < t ф < t ф2 }=фг—ФГ, t x_NОГ - mx tф = vd ’ для tф2 ^ , tФ1 = -1Ф , B m {N°Г > mx - tФ • Dx}} = Ф m ’ t1P ф m=?ехр(- x) dt ’

V 2n -“ где Фm - интеграл вероятности; tф - квантиль распределения вероятности; Вт - вероятность текущего количества КА.

Для tф = 1 значение Ф m = 0,841, для tф = 2 значение Фm =0,977, для tф = 3 значение Фm =0,998 7.

Модель 2. Количество состояний ограничено (k< n +1), значения показателей интенсивности посто

янны и равны

%к = ⁽n^{- k} )• %в, Цк = ^k •Цот ■

Математическое ожидание числа КА в ОГ (т) и дисперсия (О_х2) на любой момент времени описывается следующими выражениями:

m_{x 2}( t) =-----n--1 + ^ -е'^{L +}%в))

^{1 + ц}от / %в [   %в

^Dx 2⁽t ) = mx 2⁽t )•

^{1 +} %в / ^Цот

e^-(цот ⁺%в) t

Для стационарного состояния (t > условия

^цот ⁺ %в

)

р x 1

= ^-(1 -e¹)+ m_хо • e¹, Цот

------‘------, dx₂ = mx₂--■

^{1 + ц}от / %в             ^{1 +} %в / ^Цот

имеем

D^(t) = m^ -m • e,             (5)

где т_хо- математическое ожидание в начальный момент времени.

В процессе увеличения КА в ОГ достигается стационарный режим процесса (при (t_уст> 3/Ц_от) и в этом случае математическое ожидание и дисперсия равны

Для случая «чистой» гибели (%_в= 0) и при m_x0 = n , 0 < t < t имеем

mx 2⁽t) = ⁿ -Дот •t, ^Dx 2 ⁽t) ”Цот •t ■         ⁽¹¹⁾

mC = DC = %_в /Цот.

Модель 3. Число состояний ограниченно k< _n +1, значения показателей интенсивности постоянны и равны %_к= %_в, Ц_к= k • Ц_от. Для расчета вероятности различных состояний ОГ используем уравнение Эрланга [2; 3] вида

После прекращения восполнения ОГ(%_В = 0) начнется ее деградация по следующему закону (0 < t < t_дег):

\К 1

— • Р_ок= 1_п, к! ⁰

m^ = D= m; •e^{Ц t}.            (7)

Значение m” выбирается по формуле (5), если процесс развертывания прерывается, не достигнув стационарного состояния, или по формуле (6) для стационарного процесса.

%в IXT 1 Г%в)n 1

Ро¹ = 1 + — +... + 1 — — +... + 1 — —.

Цот (Цот ; ^к!(Цот ; ^П!

Задавая требуемое количество КА в ОГ (N,Р_Г), при

котором решается целевая задача космической системы,

%о                            %к-1            %к                             %п^-1

^Ц1                           Ц_к          ^Цк+1                            Мп

Рисунок

и полагая N0P_]< п, получим выражение для вероятности обеспечения работоспособного состояния ОГ в стационарном состоянии (PP)

n

PP (N_о^г_г> N^Р_ОТ )= ^ Р_к.          (13)

^к=N ог

Уточним смысл используемых обозначений интенсивностей %_ви ц_от.

Интенсивности отказов каждого КА [ц ] определяется его сроком активного существования (tГКА ) и вероятностью безотказной работы за срок активного существования (В^А^С):

Цот

|l n вК1С|

, КА

tГс

Интенсивность запусков КА на орбиту в варианте %_к= %_впоказывает, что его значение не зависит от количества КА в ОГ и существует ограничение на темп запуска.

Интенсивность запусков КА на орбиту в варианте %_к= (n - к)%_впоказывает, допустимость наращивания темпа запусков в зависимости от количества отказавших КА.

Определение стратегии развертывания и восполнения ОГ космической навигационной системы ГЛОНАСС. На примере создания и эксплуатации космической навигационной системы ГЛОНАСС проведем апробацию разработанных методик развертывания и поддержания ОГКСИО.

Начиная с 1972 г. в интересах навигационно-временного обеспечения потребителей создавалась космическая навигационная система на средневысоких орбитах «ГЛОНАСС». В 1993 г система «ГЛОНАСС» была принята в опытную эксплуатацию в неполном составе ОГ, а в 1995 г развернута до штатного состава [5]. В период 1996-2002 гг. было запущено 12 КА, что оказалось недостаточным из-за ограниченного tКА и привело к деградации ОГ.

С 2002 г. началась модернизация системы и обновление ее орбитальной группировки запусками КА «Гло-насс-М».

Проведем оценки различных схем развертывания ОГ системы при следующих исходных данных:

• - начальное количество КА «ГЛОНАСС» в ОГ (на конец 2005 г.) NН_г = m_хо= 13;

• - существующие КА «Глонасс» имеют вероятность безотказной работы В'_КА = 0,7 за tКА = 4,5 года ш'_:|0.(К9);

• - запускаемые КА «Глонасс-М» имеют вероятность безотказной работы ВСА^С= 0,7 за tКА = 7 лет (ц_ОТ= 0,051);

• - конечное количество КА в ОГ N0] =24.

Расчеты проведем с использованием методик развертывания и поддержания ОГ с детерминированной схемой восполнения и при случайном процессе ее восполнения при различных значениях темпа запуска (количество запускаемых КА в год - nК_А).

Фаза развертывания ОГ. По детерминированной методике по формуле (2) находим текущее значение КА в ОГ (NТ_г), а по вероятностной методике по формуле (5) находим математическое ожидание количества КА в ОГ mx и среднеквадратическое отклонение -JD (табл. 1).

На основании полученных данных по m и В получим вероятность В_тналичия работоспособных КА в ОГ (N0_Г):

вm {nТг > (mx -1;>Х )}=фm, t; = N^тг-m^X.⁽¹⁵⁾

DX

Значения вероятностей достижения заданного количества КА NТ_гдля случая расчета по детерминированной модели приведены в табл. 2. Значения вероятностей по детерминированной методике превышают 0,892. Если этого не достаточно, то необходимо применять вероятностную модель.

Анализ представленных в табл. 2 данных в позволяет сделать заключение о том, что для гарантированного развертывания ОГ из 24 КА необходим темп запусков %_В> 4,5. Сравнение двух темпов запуска при одинаковой вероятности показывает, что за счет увеличения темпа запуска (с %_В = 4,5 до %_В = 6) уменьшается требуемое количество запускаемых КА с 27 до 24 и сроки развертывания с 6 лет до 4 лет.

На основании полученных результатов сформулированы рекомендации по стратегии ускоренного развертывания ОГ МГНСС «Глонасс», которые были использованы при корректировке федеральной целевой программы «Глобальная навигационная система». Для ускоренного развертывания штатной ОГ (24 КА) необходимо обеспечить темп запуска %_В = 6, для чего потребуется развернуть вторые рабочие места.

Фаза поддержания ОГ. Фаза поддержания ОГ МГНСС осуществляется запусками КА «Глонасс-К», имеющих вероятность безотказной работы 0,7 за t КА =10 лет (ц_ог=0,035 7).

Расчет вероятностных характеристик процесса поддержания ОГ проведем по формуле (12) при %_к= %_ви

Математическое ожидание и дисперсия количества КА в ОГ

Таблица 1

Примечание. Время достижения стационарного состояния t< ---.

Дот по формуле (10) при 1к = (n - к)1в . Результаты представлены в табл. 3.

Приняты следующие показатели процесса поддержания ОГ:

• N0Г - номинальное количество КА в ОГ;

• N0_Г- допустимое количество КА в ОГ, обеспечивающее работоспособность космической системы;

• N0_Г- текущее количество КА в ОГ;

• р_от- интенсивность отказов КА;

• 1_в- интенсивность восстановления КА;

• МО (N0_Г) - математическое ожидание числа работоспособных КА в ОГ;

• Р (N0_Г> N_р) - вероятность превышения работоспособного количества КА в ОГ;

n_кд(за t(Д) - среднее количество запускаемых КА в ОГ за период, равный гарантированному сроку существования КА.

Анализ данных табл. 3 позволяет сделать заключение о допустимости использования детерминированной модели расчета программы поддержания ОГ в течение заданного срока, когда число запущенных КА за t = t (Д равно N0Г . Значения вероятностей для этого случая превышают 0,981 (строки 5,10 табл. 3).

При одинаковых темпах поддержания ОГ и вероятностях поддержания рабочего количества КА (N0_Г> N_р) структура из N0Г = 27 предпочтительнее структуры N0Г = 24, так как в ней обеспечивается большее количество рабочих КА в ОГ.

По модели 2 с ограничением на количество состояний вероятности состояния выше, поэтому ее применение предпочтительнее.

Таким образом, разработана методика развертывания и поддержания орбитальной группировки с исполь зованием как детерминированной модели, так и моделей дискретного марковского случайного процесса.

Имитационное моделирование и проведенный анализ определили область допустимого применения детерминированной модели.

Разработанная методика прошла апробацию при корректировке Федеральной целевой программы «Глобальная навигационная система» и может быть рекомендована для использования при проведении проектных исследований и технико-экономического анализа характеристик орбитальных группировок космических систем информационного обеспечения.