Методика статистического анализа стационарной кинетической модели ячейки идеального смешения

Многие процессы в технологических аппаратах могут быть описаны с помощью уравнений материального баланса химических реакций для ячейки идеального смешения. Такие модели применяются как для отдельных аппаратов, характеристики которых приближены к идеальному смешению, так и для объектов, которые можно разбить на пространственную комбинацию ячеек идеального смешения.

Бимолекулярные реакции встречаются чаще, поэтому в имитационной модели процесс взаимодействия двух веществ A и B описывается по стехиометрическому уравнению (1). Скорость этой реакции определяется уравнением:

^{C A} =- K C C A ^{λ A}C B ^{λ B} .           (1)

Система уравнений баланса потоков имитационной модели имеет вид:

v ~ „ _ T ) C g A C g B V , (2)

v ' _х T ) C C C VV , (3) где знак “~” – означает влияние случайной составляющей на значение соответствующего параметра; в уравнениях вводится знак приближенного равенства, потому что случайные факторы могут нарушить мгновенный баланс потоков; температура процесса T хотя и является переменной, но в данном процессе не подвергается стохастическому воздействию.

Графики имитационного моделирования химического взаимодействия веществ в проточном реакторе идеального смешения в стационарном режиме по уравнениям (2)–(3) приведены на рисунке.

Для параметрической идентификации имитационной модели, описываемой в уравнениях (2)–(3), удобно использовать линейный метод наименьших квадратов, который реализуется уравнением

A = ( и ( X ) ^T U ( X ) ) 1 U ( X ) ^T Y . (4)

Формулу (4) можно применять к линеаризованному уравнению (2), которое получено при логарифмировании выражений (2)–(3). В результате получается линейное уравнение вида:

y = a^ + au ( X ) + au ( X ) + a₃u₃ ( X ) . (5)

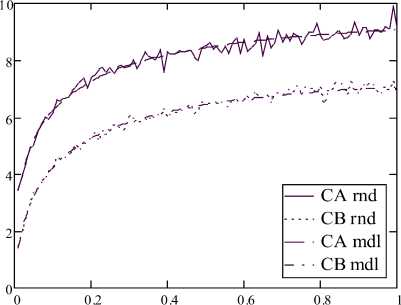
Рисунок 1. Моделирование изменения концентраций веществ A и B по уравнениям (1) и (2) в зависимости от скорости подачи раствора при заданной температуре в ячейке; САrnd, СВrnd – рандомизированные по закону нормального распределения; САmdl, СВmdl – средние, без стохастической составляющей

Figure 1. Modelling of changes in concentrations of substances A and B by equations (1) and (2) depending on the flow rate of the solution at the specified temperature in the cell; САrnd, СВrnd – randomized under the law of normal distribution; SA САmdl, СВmdl – middle, without stochastic component

Элементы уравнения (5) преобразуются из уравнения (2) с помощью следующих соотношений:

У = In (v) + In ( C- - C- ),(6)

X = {т, C-, C,},(7)

ao = In ( kо) + In (V ),(8)

a1 =- Et,(9)

R a2 = g, a3 = AB,(10)

«,(X ) = 1, u ( X ) = In CA u ( X ) = In CB .(12)

Для определения значений элементов матрицы A были получены экспериментальные данные методом планируемого имитационного эксперимента «34» с тремя уровнями и четырьмя независимыми факторами в условиях стохастической неопределённости 1–5% (всего 81 точка).

Применяя выражение (4) к экспериментальным данным, преобразованным с помощью выражений (6)–(12), получается матрица коэффициентов уравнения (5):

А = (-3,507; - 239,789; - 0,9; - 1,099).

Провели исследование полученной модели на адекватность результатам имитационного моделирования (рисунок 1). Для этого разделили показатели и независимые параметры в правой и левой частях линеаризованного уравнения (5) и уравнения материального баланса (2):

ln ( V ) + In ( C, - C, ) = ln(KC) + In(V) + g, ln(C,) + Л, ln (C,), (13) v (        ,) = Kc (T)Cg-Cg-V.   (13)

Провели оценку адекватности с помощью F- критерия и гипотезы о неоднородности дисперсий случайных процессов и функции. Для этого вычислили отношение двух дисперсий, которое является оценкой значения F- критерия для выборки наблюдений:

F = D m^

^D min

где F – табличное значение F- критерия, которое рассчитывается с помощью функции qF ( a , f mах , f min ).

Задачей определения адекватности с помощью F – критерия являлась проверка гипотезы о том, что случайные изменения наблюдаемых значений в экспериментальных точках и отклонения значений функции от средних наблюдений вызваны разными случайными процессами. Если дисперсии однородны, то аппроксимация экспериментальных данных фактически превращается в интерполяцию, и функциональная зависимость не описывает с выбранным уровнем надежности неслучайные закономерности.

Определили дисперсию воспроизводимости левой части уравнения (13) по формуле

На главной диагонали матрицы D находятся оценки дисперсий коэффициентов уравнения (13). Доверительные интервалы рассчитали по формуле

I j = t a ,AD C0Vj^ , ( J = ⁰, -³ ) •

где a - доверительная вероятность; f - число степеней свободы.

Результаты расчета приведены в примере 1.

D Y

Y N 1Y m 7 y. - y 7

_ Z—i j =0 Z—n =0 \ ^jJ ⁷ J , ч

Пример 1. Анализ доверительных интервалов коэффициентов модели.

Вычисляем матрицу дисперсий-ковариаций коэффициентов:

N ( m - 1 )

i := 0 .. 3

Определили дисперсию адекватности модели как отношение суммы квадратов отклонений расчетных значений от средних к числу степеней свободы, равному разнице между числом экспериментов и коэффициентов модели:

DC :=

DC =

D Yad =

^m E^ ( yj ~ a 0 - a l u1 ( X ) - a 2 u 2 ( X ) - a 3 u 3 ( X ) ) N - 4

Для уравнения (14) вычислили дисперсии воспроизводимости и адекватности:

D G

E N -1v"' m -1 /          \²

_   j =0 L = 0 ⁽ g j ^- g jii )

N ( m - 1 )

De а =

Gad

m E N -K g , - F ( A , X ) ) 2

N - 4

где F ( A, X ) - правая часть уравнения (13); A – матрица коэффициентов; X – матрица параметров.

Имитационное исследование показало, что условие (15) выполняется при повышении точности поддержания параметров и измерения показателей моделирования. Можно отметить, что уравнение (14) дает большую однородность, чем уравнение (13), что справедливо для исходного уравнения.

Провели оценку доверительных интервалов коэффициентов линеаризованного уравнения с помощью t – критерия. Целью данного оценивания являлось определение значимости коэффициентов для выбранной формы уравнения. Коэффициент считается значимым, если его абсолютная величина больше соответствующего доверительного интервала.

Для этого вычислили матрицу дисперсий-ковариаций коэффициентов:

D cov = D Y ( U ( X ) T U ( X ) ) ^{- 1} .

(ut-u) 1

(        -4

2.295 x 10

- 0.07 - 4.601 x 10 6

- 4.601 x 10 6

- 0.07

22.768

- 4.601 x 10 ^{- 6}

_V- 4.601 x 10 ⁶

qt(0.95,N - m) = 1.648

I i

2.787 x 10 6

2.787 x 10 6 _v

(I)

= qt(0.95 , N - m) . ^DC"”

I =

Г

0.025

7.863

A

- 3

2.751 x 10 3

V 2.751 X 10 ³ J

< - 3.507 A

A =

- 239.789

0.9

V 1.099 J

Полученные в результате расчета в матрице I доверительные интервалы значительно меньше по абсолютной величине значений коэффициентов модели, приведенных в матрице A:

к, ^ A , , ( i = 0, ^ ,3 ) .

Следовательно, рассчитанные коэффициенты модели являются значимыми.

Оценили доверительные интервалы концентраций веществ на выходе из ячейки с помощью t – критерия:

I X = t a , f x V D X " •            ⁽¹⁶⁾

где D – оценка дисперсии концентрации

вещества X в выходном растворе (А или В); f – число степеней свободы.

Целью данного оценивания является проверка гипотезы о значимости параметров модели в исследуемой области.

Оценку дисперсии выходных веществ рассчитали по формуле

D X

E N -lx^-' m /_ \2

j =0 Z , =0 ( x j ^- x j J

N - m

где x – среднее значение концентрации вещества X в выходящем растворе в j -й точке плана экспериментов, x – наблюдаемое i- е значение в j -й точке.

Результаты вычислений дисперсии и доверительных интервалов по формулам (16) и (17) приведены в примере 2.

Пример 2. Определяем доверительные интервалы выходных концентраций:

DA :=

DB ^:=

N - 1  4

Z Z ( ^CAmdlj ^{- Par_Cout}j , . ) ² j = о i = о ^V

N - m

N Z ZZ ( CBmdl - Par-Cout. ) ²

j = 0 i = 5

N - m

1д := qt(0.95,N-m)- /da Ib := qt(0.95,N-m)- /DBIa = 1.013 IB = 0.892

Значения доверительных интервалов составили: для вещества A – 1,013 и для вещества B – 0,892. Такие отклонения обусловлены