Методологические основы использования индуктивных производственных функций в задачах обоснования инновационно-инвестионных решений

1. Развитие базового для технологий построения производственных функций понятия «технологическая функция»

Учёными-экономистами и производственниками-практиками давно замечено и доказано, что традиционная дедуктивная производственная функция описывает лишь эффективные технические способы, т. е. такие, когда производится максимум желаемого товара при данных объёмах ресурса либо затрачивается минимум ресурса для установления заданных размеров производства. Процесс нахождения таких технических способов долгое время даже не рассматривался, а соответствующие вопросы относились к задачам управления, выходящим за рамки экономики. В конце концов, стало ясно, что нужно перенести центр внимания снова на предприятие (фирму) с целью изучения её внутренних решений, и тогда можно не только получить экономию, но и обрести углублённое понимание предмета.

Современное развитие экономической теории на основе сведений о технологических процессах дало повод к разработке производственных функций и функций затрат с использованием технических знаний из повседневной инженерной практики. Подход к производственной функции на технической основе имеет значительные преимущества, поскольку, во-первых, становится известной область применения функций, а во-вторых, появляется возмож- ность относительно легко включить в модель результаты технического прогресса, так как они не связаны с жесткими рамками фактических наблюдений. Производственные функции данного класса как более узкое понятие, не включающее фактор предпринимательства и ряд других нетехнических процессов (продажа товаров, человеческий фактор и др.), получило название «технологические функции»[1].

Технологические условия развития производства наиболее полно исследованы на практике на основе анализа деятельности предприятия. Производственное множество значительно упрощается. Нужно отметить, что существует конечное число однородных товаров и также конечное число базисных технологических методов. Каждый базисный метод характеризуется некоторым числом для каждого товара – отрицательной величиной для затрат ресурса и положительной величиной для выхода продукции. Технические знания общества, достигнутые на сегодняшний день, вложены в эти базисные методы и в применении они считаются постоянными и воспроизводимыми. Методы должны быть аддитивными. Это означает, что они независимы друг от друга и что один метод можно совместить с другим, образовывая новый в широком смысле метод, состоящий из сочетания величин исходных методов. Каждый частный метод независим от других и между ними нет взаимодействия. Методы считаются

бесконечно делимыми (декомпозируемыми) и пропорционально воспроизводимыми.

Значительным событием экономической науки в области теории организации (предприятия) стало развитие технологических функций на основе моделей линейного программирования, решающих ряд оптимизационных задач для краткосрочного периода с фиксированным предложением ряда ресурсов, с учётом изменения самих производственных отношений.

При сравнении подхода на основе линейного программирования с эмпирическим исследованием традиционных производственных функций следует иметь в виду, что, с одной стороны, модель линейного программирования обычно интерпретируется как модель производства в коротком периоде с фиксированным предложением ряда ресурсов. С другой стороны, эмпирическое использование производственной функции Кобба-Дугласа обычно связано с долгосрочными соотношениями, в которых объём ресурсов может изменяться. Решение задачи с помощью модели программирования указывает, что организация (предприятие) должна делать, чтобы максимизировать свой доход. А это в некотором смысле улучшает существующую производственную функцию предприятия: повышается уровень ее эффективности. Подход на основе линейного программирования позволяет не просто описывать производственные отношения, а, как правило, их изменять.

Указанные «скромные» результаты и ограниченность области применения нового подхода к построению индуктивной производственной функции предприятия являются следствием того, что применение инженернотехнических данных для решения задач инновационного инвестирования «ещё переживает период младенчества».

Самый известный и чаще всего применяемый на практике подход к анализу эффективности производства строится на статистических данных и на принципе «от общего – к частному, от отрасли – к предприятию» – это так называемый дедуктивный подход. Использование такого подхода для анализа инвестиционных процессов не всегда оправданно. И тогда обоснованно возникает потребность в предметной связи с производством, технологией, ресурсами, т. е. с самой сутью инвестиционных изменений. Поэтому сегодня естественной альтернативой такому подходу может стать индуктивный подход, который предполагает построение производственной функции на разных уровнях: от элементарных участков или экономических ресурсов к предприятию и экономическим ресурсам в целом.

Индуктивные производственные функции в качестве альтернативы к сложившемуся дедуктивному подходу к их построению, использующие для инвестиционного исследования знания технологии производства, его структуры и организации, впервые были исследованы учеными-экономистами П. Дугласом и А. Уолтерсом в конце 40-х и начале 60-х гг. прошлого века.

Американский ученый П. Дуглас в 1948 г. в статье «Существуют ли законы производства?» предложил использовать не агрегированные отраслевые показатели, а средние данные по отдельным заводам для последующего обобщения [1]. Сложность реализации данного подхода в то время ограничила его дальнейшее развитие. Новым толчком к продвижению идеи индуктивного исследования реального производства послужила работа британского экономиста А. Уолтерса «Производственные функции и функции затрат: эконометрический обзор» (1963 г.), где был выделен класс технологических функций, использующих технические знания о производстве из инженерной практики [5]. Тем самым было предложено дальнейшее перемещение начала индуктивного исследования внутрь производства (предприятия). Тогда эта идея не получила дальнейшего развития, так как не соответствовала масштабам инвестиционной политики и уровню развития научнотехнического прогресса.

Актуальность и востребованность развития данного подхода при изучении реального производства в наше время научно была подтверждена несколько лет назад в диссертационном исследовании И. В. Ёлоховой «Концепция индуктивного представления производственной функции в задачах модернизации инвестиционных процессов» (Пермский технический государственный университет) и одобрена член-корреспондентом РАН Г. Б. Клейнером.

В связи со сравнительно узкой предметной областью исследования, ограниченной рамками инвестиционных моделей, а именно фактором инвестиционного капитала, все другие экономические факторы (ресурсы, средства) обеспечения производства – природные, трудовые, капитальные (физический капитал), человеческие и проч., могут быть сведены к обобщающему фактору – инвестиционному капиталу по затратной (аддитивной) схеме.

Индуктивная производственная функция отличается от функций совокупных затрат (издержек) присутствием цены ресурса, влияющей на объём возвращаемых инвестору средств, а также математическим отношением, имеющим место при приведении её к функциями, принимающим часто достаточно сложные в аналитическом смысле формы. Последнее обстоятельство преодолевается в процессе имитационного моделирования динамики процесса производства посредством перемены мест и табличных результатов вычислительного эксперимента «затраты-выпуск», выполняемого по технологической схеме производства, т. е. согласно содержанию технологической функции с учётом особенностей реального производства.

Основания новой парадигмы моделирования инвестиционных процессов на промышленных предприятиях, строящиеся на индуктивном представлении производственной функции, конструируемой на основе технологической функции с использованием технических знаний из повседневной инженерной практики, способствуют созданию более эффективных инструментальных средств поддержки принятия инновационно-инвестиционных решений и анализа эффективности производства.

Рассмотрим процедуру преобразования технологической функции в индуктивную производственную функцию. При этом данную процедуру целесообразно рассмотреть поэтапно, последовательно отказываясь от технологических подробностей в пользу увеличивающегося экономического наполнения, сохраняя взаимосвязи обоих аспектов, обеспечивающих востребованность в задачах совершенствования бизнес-процессов особых свойств индуктивной производственной функции [4].

Исходной позицией для искомого преобразования может стать базовая технологическая функция, описывающая производство некоторого продукта в самой общей форме, безотносительно к техническим возможностям конкретного предприятия. Она представляет интерес для профессиональных технологов, инженеров, ответственных за размещение данного продукта в заданной производственной среде.

На начальной стадии преобразования (после распараллеливания возможных параллельных технологических линий) технологическая функция представляет собой описание выпуска конечного продукта в виде последовательности процессов и полагаемых допустимыми методов указанных процессов с учётом необходимых для каждого метода ингредиентов, материалов и т.п. Это можно иллюстрировать ориентированным графом (рис. 1), вершинами которого являются отдельные фазы производства, а дугами – множества допустимых методов построения указанных процессов, отличающихся производительностью, себестоимостью, потреблением ресурсов и др.

Фаза

Процесс1

Методы М1

Процесс 2

Методы М 2

Процесс 3

Фаза 1

Рис. 1. Базовая технологическая функция

Методы М3

Процесс i

Методы М i

Любой путь в таком ориентированном графе порождает одну из реализаций базовой технологической функции в виде последовательности пар «процесс-метод».

Базовую технологическую функцию можно описать эквивалентной таблицей (матрицей), представленной в табл. 1, произвольный элемент которой может принимать два значения:

• a)    a ij = 0, если обозначает недопустимость в i -м процессе метода m _: е M, ;

ji

• б)    а_п = 1, если это означает допусти- ij

мость в i -м процессе метода m_: е M_: .

ji

Методы, представленные на рис. 1 и в табл. 1, порождают множество вариантов реализации базовой технологической функции. При этом замена одного варианта другим происходит посредством операций замещения методов в каждой группе М_{i .}

Для экономического анализа базовая технологическая функция может быть освобождена от жесткого порядка следования и ряда других обязательных и существенных для технологии атрибутов, а при необходимости локально сгруппирована.

Таблица 1

Базовая технологическая функция

Методы	Процесс
1	а 11	а 21	а 31	...	ai 1
2	а 12	а 22	а 32	...	ai 2
...	...	...	...	...	...
М i	a1 Mi	a 2 Mi	a3 Mi	...	aiMi
...	...	...	...	...	...
М	a 1 M	a 2 M	a 3 M	...	aiM

В интересах экономического анализа табл. 1 может быть модифицирована в табл. 2 заменой a ij —— b ij = 1/ C j , где C - ориентировочные затраты на i -й процесс, реализуемый по j -му методу, при производстве единицы конечного продукта.

Используя новую форму технологической функции, технолог получает дополнительные возможности для маневра. Это касается определения принципиальной возможности выпуска продукции на имеющихся производственных мощностях, установления допустимых вариантов технологического процесса с учетом ограничений на совместимость и физическую реализуемость указанных в технологической функции методов и, наконец, обеспечения выбора наилучшего в определенном смысле варианта выпуска продукции. В этом случае можно говорить о том, что базовая технологическая функция преобразована в технологоэкономическую функцию выпуска заданного продукта на данном предприятии.

Дальнейшее преобразование технологоэкономической функции выпуска связано с учетом факторов производства Х через экономическую функцию затрат С_; (( 3 ) ) факторов производства (табл. 2) на ϑ единичных операций процесса i , без учета его загрузки другими заказами.

Таблица 2

Экономическая функция затрат факторов производства

Ресурсы Xk	Процессы Пi
	Заготовка 1	Обработка 2	Сборка 3	Наладка 4	i
1.Энергоресурсы	С n( ^ 1 )	C 21 ( ^ 2 )	С 31 ( ^ 3 )	С 41 ( ^ 4 )	CM)
2.Материалы, сырье	С nW	С 22 ( ^ 2 )	С 32 ( ^ 3 )	С 42 ( ^ 4 )	CM i)
3.Трудовые ресурсы	c nW	С 23 ( ^ 2 )	С 33 ( ^ 3 )	С 43 ( ^ 4 )	CM)
4.Производственные   пло щади	c mW	С 24 ( ^ 2 )	С 34 ( ^ 3 )	С 44 ^ )	CM)
k …	С 1 k W	c 2 k W	c 3 k W	С 4 k ( ^ 4 )	C * ( ^ i )

Для анализа эффективности полной загрузки производства можно построить экономическую функцию затрат факторов производства c учетом его загрузки другими заказами по фак- ту накопленных затрат к моменту поступления нового заказа С 0 (табл. 3).

Таблица 3

Экономическая функция затрат факторов производства c учетом его загрузки другими за- казами

Ресурсы X k	Процессы П i
	Заготовка 1	Обработка 2	Сборка 3	Наладка 4	i
1.Энергоресурсы	С 0 + G W	С 0 + С 21 W	С 0 + С 31 W )	С 401 + С 41 W	с + С w
2.Материалы,  сы рье	c 0 + G2 W )	С 202 + С 22 ( ^ 2 )	С 302 + С 32 W 3 )	С 402 + С 42 W	C i2 + C 2 W
3.Трудовые ресур сы	С 103 + CnW	С 203 + С 23 ( ^ 2 )	С 303 + С 33 ( ^ 3 )	С 403 + С 43 ( ^ 4 )	С 3 + g w
4.Производственны е площади	С м + Q W	С 24 + С 24 ( ^ 2 )	С 304 + С 34 W 3 )	C0 44 + С 44 W	с . + С 4 Ш
k …	С к + С 1 к W	С 0 к + С 2 к W	С 30 к + С 3 к W	С 40 к + С 4 к W	с к + С к W

Полный экономический анализ эффективности производства нового продукта требует перехода к экономической функции выпуска продукции в количестве Q (табл. 4) подстановкой i ^ ^ nQ , где n^ - количество операций W , затрачиваемых на производство единицы конечного продукта Q.

Экономическая функция выпуска продукции (табл. 4) является последней фазой преобразования технологической функции на основе аддитивной операции перед построением семейства производственных функций самого различного назначения из семейства совокупных затратных функций.

Таблица 4

Экономическая функция выпуска продукции

Ресурсы X k	Процессы Пi
	Заготовка 1	Обработка 2	Сборка 3	Наладка 4	i
1.Энергоресурсы	Сп + С 11 ( Q )	С 201 + С 21 ( Q )	С 01 + С 31 ( Q )	С 401 + С 41 ( Q )	с 0 + С 1 ( q )
2.Материалы, сырье	С 102 + С 12 ( Q )	С 202 + С 22 ( Q )	С 302 + С 32 ( Q )	С 402 + С 42 ( Q )	С к + С г ( Q )
3.Трудовые ресурсы	С 103 + С 13 ( Q )	С 203 + С 23 ( Q )	С 03 + С 33 ( Q )	С 403 + С 43 ( Q )	С 03 + С 3 ( Q )
4.Производствен-ные площади	С 104 + С 14 ( Q )	С 204 + С 24 ( Q )	С 304 + С 34 ( Q )	С 404 + С 44 ( Q )	С к + С Л Q )
k …	С к + С 1 к ( Q )	С 20 к + С 2 к ( Q )	с 30 к + С 3 к ( Q )	С к к + С 4 к ( Q )	С к + С к ( Q )

Основные виды совокупных затратных функций:

• а)    полная совокупная затратная функ-

• ция:С (Q)  VV (C« + Ck (Q));

ik

• б)    совокупная затратная функция по

фактору k : С _к ( ^Q ) = ^ ^{( C}ik + C k ( ^Q )) ;

i

• в)    совокупная затратная функция по процессу i : С ^{( Q} ) = ^ ⁽ Cl + C к ^{( Q} )) ;

k

• г)    агрегированная относительно процесса i совокупная затратная функция по фактору

к: С к ( Q ) = z ( C k + C k ( Q )) + C k, + C ik ( Q ) ;

^ i

• д)    агрегированная относительно фактора k совокупная затратная функция по процессу i:

• 2. Два подхода к задаче моделирования индуктивной производственной функции

С ( Q ) = Z ( C k + C „ ( Q )) + C k + C k ( q ) . k ] * k ]

Выбор типа затратной функции и, соответственно, производственной функции зависит от содержания задачи инновационноинвестиционного исследования эффективности производства. Тип затратной функции может меняться сообразно обстоятельствам бизнеса, оправдывая известную трудоемкость получения (см. табл. 1 – 4) многократностью использования и достаточным обоснованием принимаемых решений.

Одним из важнейших направлений экономических реформ в современной России сегодня следует считать модернизацию реального производства путём развития и повышения эффективности инновационно-инвестиционной деятельности на промышленных предприятиях. В настоящее время в экономике России сложилась непростая ситуация, когда сложные задачи поддержания высоких темпов экономического роста, диверсификация производства, внедрение энергосберегающих технологий, понижение уровня инфляции и повышение конкурентоспособности отечественных товаров пока не могут быть в полной мере подкреплены соответствующей динамикой инвестиций. Потребность в коренном обновлении отечественной промышленности на базе применения научнотехнических достижений, высоких технологий, современной организации производства и труда требуют значительных инвестиционных вложений за счет всех источников финансирования: государственных, муниципальных, сторонних инвесторов, средств предприятий – как собственных, так и привлеченных. Сегодня требуются долгосрочные, устойчивые, опережающие динамику ВВП темпы прироста инвестиций в основной капитал с тем, чтобы не просто восстановить необходимый его запас в экономике, но и провести его всеобъемлющую модернизацию, обеспечив научно обоснованные возможности выпуска отечественными предприятиями конкурентоспособной продукции не только внутри страны, но и на международном уровне. В то же время, как показал опыт последних лет, инерционное развитие этого процесса не даёт желаемых результатов. Для преодоления инерционности необходима более четкая экономическая политика активного стимулирования инновационно-инвестиционных процессов со стороны государства как по отношению к бизнесу, так и по отношению к государственным и муниципальным предприятиям. А главное, нужна координация совместных усилий государства и бизнеса в реализации поставленной цели с жёстко определёнными взаимными обязательствами, сроками и конкретными результатами, которые должны быть получены в итоге совместных действий.

Ключевую роль в исследовании любого промышленного объекта играют его модели, основное назначение которых состоит в предоставлении информации о прототипе [6]. Привлекаемые для этого модели должны быть адекватны как объекту, так и целям его исследования, в данном случае – выявлению эффективных вариантов инвестиционных решений, способных на инновационной основе кардинально улучшить производственное, технологическое, финансовое состояние предприятия, вывести его из назревающего технологического и экономического кризиса и достичь более высокого уровня развития.

Указанным целям вполне соответствует моделирование экономической деятельности предприятия в образе производственной функции. Особое внимание в подобных исследованиях должно быть удалено индуктивной производственной функции, обеспечивающей соответствие между количеством ресурсов, требуемых для производства того или иного объема выпуска, и самим этим объемом выпуска. Производственная функция отображает максимальные объемы выпуска, которые могут быть произведены с помощью того или иного количества ресурсов при данном уровне технических (инженерных) знаний.

Ученые-экономисты давно и правильно определили, что производственная функция является действенным и эффективным инструментом, позволяющим оценить производственный потенциал любого предприятия. Производственные функции будут применяться в экономических исследованиях и приносить реальную пользу только в том случае, если они как модели взаимосвязи «затраты-выпуск» будут адекватно отражать реальную действительность. Поэтому важная задача теории – разработка достоверных и практически применимых методов построения производственных функций.

Из сказанного выше следует, что для построения производственных искомого типа функций нужно знать современную технологию производства, ее структуру и организацию, а также принципы работы сложных машин и оборудования. Считается, что знания всего этого сложного производственного механизма не требуется, если владеть эффективными математическими инструментами. Речь идет об использовании методов регрессионного анализа статистических данных о затратах и выпуске продук- ции. Сложившаяся парадигма экономического исследования, в основе которой лежит концепция экономико-статистического представления производственной функции, не в состоянии в полной мере обслуживать современную инвестиционную практику, нуждающуюся в более предметной связи с реальным производством, непосредственно воспринимающим предлагаемые модернизационные и инновационные изменения. Данный подход, отличающийся аппроксимационным принципом образования цепи последовательных приближений от общего описания объекта (модели) к частным целям исследования, в современных исследованиях называется дедуктивным, а представление производственных функций как переход (гомоморфизм) от объекта к его моделям – дедуктивным представлением производственных функций [3].

Чтобы изменить ситуацию коренным образом, нужно сделать моделирование инвестиционных процессов на основе производственных функций мощным инструментом конструирования действенных, эффективных направлений совершенствования работы любого предприятия. И это можно сделать лишь в рамках нового основания парадигмы экономического исследования – индуктивного представления производственной функции, концентрирующей и развивающей накопленный десятилетиями опыт разработки и применения технологических производственных функций, основанных на инженерных расчетах, и способной служить методологической базой при создании инструментальных средств поддержки принятия инновационно-инвестиционных решений.

Ниже рассматриваются возможности соединения исследования реального производства и рынка на основе индуктивного подхода и упрощения процедур анализа и синтеза посредством кусочно-линейной аппроксимации затратных / технологических функций [4].

Индуктивное представление производственных функций промышленного предприятия строится на основе описания затратных функций (совокупных издержек) экономических ресурсов и технологий, определяющих реальный производственный процесс (рис. 2).

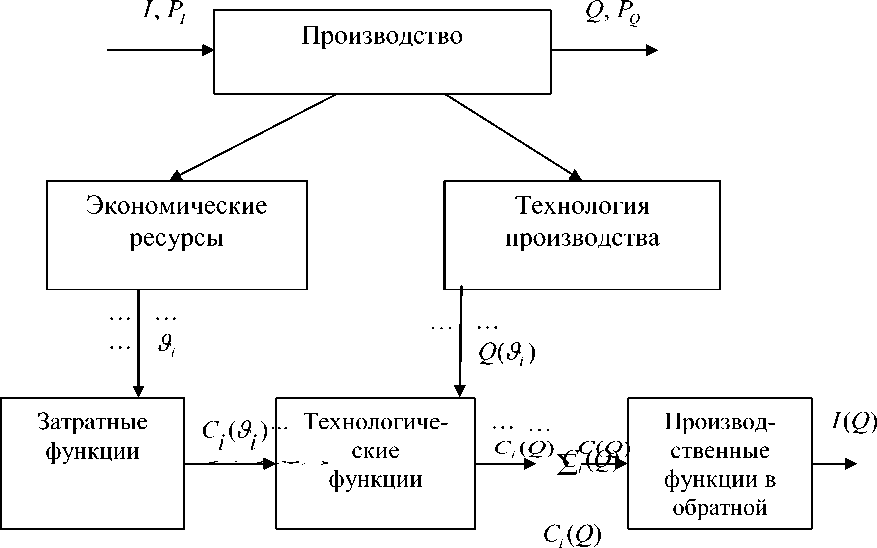
Рис. 2. Индуктивное представление производственных функций реального производства

Экономические ресурсы как фундаментальное понятие экономической теории означают источники, средства обеспечения производства. Они делятся на природные (сырьевые, географические), трудовые (человеческий капитал), капитальные (физический капитал), оборотные (материалы), информационные и финансовые (денежный капитал) ресурсы.

Затратные функции С ( ^ ) могут быть описаны аналитическими средствами, заданы графически или таблично. Их общим свойством является неубывание расходуемого количества определенного экономического ресурса С с ростом объема выпуска С ( ^ ) при ограничениях различного характера (рис. 3).

Затратные функции традиционно не связаны непосредственно с технологией произ- водства конечного продукта и в своей массе – многообразны. Для использования затратных функций при конструировании производственных функций их следует определенным образом модифицировать, учитывая принятую технологию и агрегируя множество производственных факторов в универсальный фактор денежного выражения.

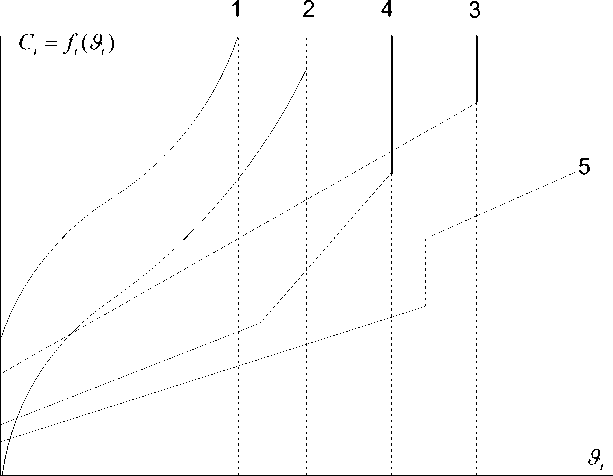
Рис. 3. Непрерывные затратные функции: гладкие с постоянными затратами (1) и без таковых (2), линейные (3) и кусочно-линейные (4) с ограничениями и разрывами 1-го рода (5)

Смысл модификации затратных функций С ( ^ ) - приведение их к технологическим функциям C_t ( Q ) , т. е. к количеству произведенного согласно принятой технологии Q ( ^ ) основного продукта Q, для получения возможности простого суммирования технологических функций по каждому экономическому ресурсу (рис. 4), с целью построения совокупной технологической функции.

Отождествляя совокупные затраты с востребованным инвестиционным капиталом I , мы приходим к индуктивной модели однофакторной (по инвестиционному капиталу) обратной производственной функции I ( Q ) .

В тех случаях, когда для экономического анализа необходима производственная функция промышленного предприятия в прямой форме Q ( I ) , следует найти способ обращения функции I ( Q ) .

Следует заметить, что присутствующая виртуально в качестве слагаемых в полученной производственной функции совокупность технологических функций продолжает оставаться объектом инновационно-инвестиционного внимания, что существенно отличает данный класс производственных функций от традиционных, дедуктивных. Под этим углом зрения следует проводить экономический анализ производства для установления имеющихся и достижимых интервалов рентабельности и оптимальных рабочих точек внутри этого интервала. Решение подобных задач следует связывать с предельными производственными функциями в прямой dQ(I) / dI или обратной dI(Q) / dQ формах.

Однако производственные функции, полученные на основе технологических функций, не отображают факторы предпринимательства, рынка и других проявлений человеческого фактора. Этот недостаток можно преодолеть подключением к экономическому анализу на основе индуктивной производственной функции категорий рыночных цен на конечный продукт P и инвестиционный капитал P , лучше всего в форме прямого P_t / Pq либо обратного P g / P_I отношений.

Для производственных функций в прямой форме Q ( I ) производная dQ / dI имеет одинаковую размерность с отношением Pj / Pq , что допускает их сопоставление.

Интерпретации обеих категорий, несмотря на одинаковую размерность, различны. Предельная производительность характеризует прирост производства в денежном выражении на единицу инвестирования, а отношение рыночных цен – соразмерность платы за инвестиции (расходная составляющая) и компенсации издержек по мере успеха на рынке готового продукта (прибыль).

Вариант сложившихся рыночных отношений P / Pq может быть сопоставим с текущими рабочими точками предельной производственной функции: р / Pq = dQ / dI или PdI = P_QdQ .

Полученное равенство свидетельствует о наличии баланса между расходами на приращение инвестиций и дополнительной прибылью на рынке готовой продукции.

Нарушение баланса в сторону dQ' / di < dQ / di от точки (Q, I^ ) ведет к отношению P;di > PQdQ , что говорит о левой Qmin (I) = Q(Iтоп ) (соответственно правой от точки (Q, 1 max ), Qax (1) = Q(1^ ) ) гРанице рентабельности производственной функции и существовании (в случае непрерывной дифференцируемости функции Q(I) ) оптимального решения Q^ = Q(Iopt) .

Аналогичные результаты могут быть получены с помощью производственной функции в обратной форме для равенства Pq / Р_; = dI / dQ , откуда условие равновесия примет вид: pdQ = PjdI .

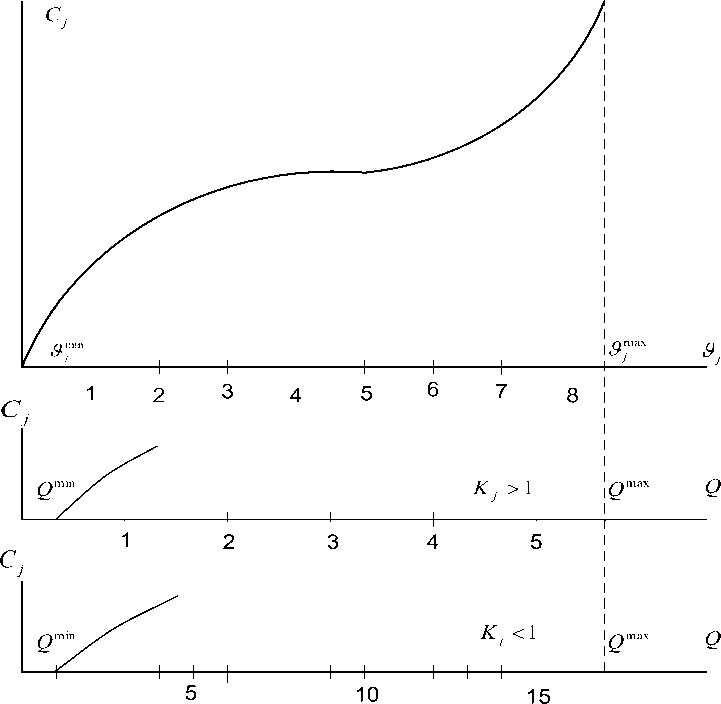
Рис. 4. Приведение затратной функции к единому аргументу

– количеству произведенного основного продукта, т.е. к технологической функции

Реальные объекты порождают на этой основе множество разнообразных моделей в соответствии с конкретными особенностями рынков капитала и основного продукта, а также затратных/технологических функций и инновационно-инвестиционных взглядов на них, тесно связывая рынок с реальным производством.

Аналитические решения при задании множества значений выпуска продукции, каж- дая из которых отвечает условию предельной отдачи, не всегда существуют, что приводит к необходимости применения достаточно сложных методов имитационного моделирования для нахождения предельной формы производственной функции (в приращениях). В любом случае необходимо определить производную от функции промышленного предприятия в прямой форме с последующим нахождением подобла- сти рентабельности. Если к этому добавить условия спроса - ограниченность и эластичность, то область рентабельности становится еще более сложной для идентификации.

Аппроксимация индуктивных производственных функций позволяет существенно упростить процедуры представления и использования этой важнейшей категории экономического исследования промышленных предприятий [2].

Исследование процедур моделирования инвестиционных процессов при аппроксимации индуктивных производственных функций проводится по следующей схеме:

• -    описание процедуры аппроксимации затратных функций методом кусочно-линейной аппроксимации;

• -    исследование процедур формирования модификаций линеаризованной производственной функции;

• -    обобщение полученных результатов на случай множественной кусочно-линейной аппроксимации.

После линеаризации совокупных затратных функций общая функция затрат в соответствии с аддитивно-последовательной процедурой, в ходе которой количество участков линейной аппроксимации может меняться (см. рис. 5) за счет внутреннего дробления (возрастать) и в связи с появлением более жестких ограничений, сокращающих область определения формируемой общей функции издержек (уменьшаться).

В результате кусочно-линейной аппроксимации затратных функций и аддитивно -последовательной процедуры формируется приближение к производственной функции в обратной форме. Это приближение в общем случае содержит n линейных участков, имеющих внутри первую производную, имеющую разры- вы 1-го рода в общих с соседними участками точках.

Если область определения каждой совокупной затратной функции разбить на то же самое число интервалов (на рис. 5 это участки [ Q 0 , Q 11 [ Q 1 , Q 21 [ Q 2 , Q 31-) , ^то произвольный i -й участок производственной функции может быть описан как линейная функция:

Cj ( Q ) = a 0 + a Q , Q e

\o‘ = 0‘ ^-1 0‘ = 0‘ ⁺¹1 min      max , max      min

Таким образом, любая индуктивная производственная функция промышленного предприятия может быть представлена в приближенном виде на основе кусочно-линейной аппроксимации семейством элементарных совокупных затратных функций с последующим их аддитивно-последовательным объединением в единый математический объект. Новая форма представления индуктивной производственной функции ценой введения погрешностей в контролируемом объеме способна объективно отображать все необходимые данные для эко- номического исследования инвестируемого предприятия. Конструирование индуктивной производственной функции и её использование в рамках предынвестиционного экспресс-анализа не требуют применения трудоемкого имитационного моделирования, поскольку они не связаны с нелинейностями высших порядков, сложностью получения производственной функции и ее предельных модификаций в прямой форме. Это существенно облегчает анализ решающих правил при принятии инновационно -инвестиционных решений. Для построения линеаризованной производственной функции достаточно последовательно, начиная с нижнего интервала, определить все интервальные границы и соединить их между собой, образуя единую область определения.

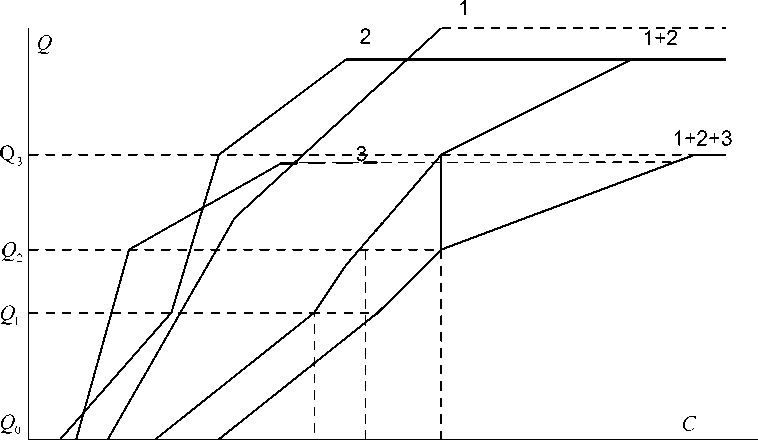
Рис. 5. Формирование общей функции совокупных затрат C ( Q ) посредством аддитивно-последовательной процедурой

Проблему аппроксимационного подхода к конструированию индуктивных производственных функций представляет их многозвенность как результат кусочно-линейной аппроксимации, хотя во многих случаях реального производства это свойство может быть и не сильно выражено. Выход из этой ситуации подсказывает определенный изоморфизм математических описаний различных между собой ли-

Q

Q 6

неаризированных участков. Это обстоятельство позволяет сделать вывод о целесообразности и допустимости разработки алгоритмических основ предынвестиционного анализа промышленного предприятия для случая линейного представления индуктивной производственной функции без разрывов 1-го рода и ее производных (рис. 6) с последующим обобщением полученных результатов на более сложные случаи.

µ Q ₆

Q 5

Q 4

Q 3

Q 2

Q 1

Q 0

µ Q ₅

^µ Q 4

^µ Q 3

µ Q ₂

^µ Q 1

µ Ι ( Q ) = d Ι /dQ

Рис. 6. Предельная аппроксимированная производственная функция в обратной форме d i ( Q ) / dQ = ^ ( Q )

Свойство аддитивности затратных функций (обратных производственных функций, или производственных функций в обратной форме) позволяет выделить в качестве одного из слагаемых любой экономический фактор, выражаемый в единицах шкалы информационного ресурса.

Возможность сопоставления индуктивной производственной функции и её предельных модификаций при наличии и отсутствии выбранного экономического фактора, а также с «желаемыми» (удовлетворяющими потребности инвестора и реципиента) параметрами позволяет ставить и решать задачи «экономического» конструирования инвестиционных процессов, формируя задание на инновационные предложения в экономических категориях.

Наконец, индуктивный характер процедуры построения производственной функции, охватывающей все экономические факторы реального производства с необходимой степенью детализации, допускает к модельному исследованию практически неограниченный спектр инновационно-инвестиционных задач по модернизации или совершенствованию конкретного производства, как полномасштабных (достаточ- но трудоемких), так и упрощенных – в рамках экспресс-анализа.