Методы гранулирования нечѐтких временных рядов для анализа данных

Климатические изменения оказывают значительное влияние на социальноэкономические системы, что обуславливает необходимость разработки новых подходов к прогнозированию и принятию решений. Рост объёмов данных, их неопределённость и сложность структуры делают традиционные методы анализа недостаточно эффективными. Актуальной задачей становится разработка методов, способных обрабатывать большие объёмы данных с учётом их неопределённости и обеспечивать достоверность данных в системах поддержки принятия решений (СППР). Перспективным направлением в этой области является использование нечётких временных рядов, которые позволяют учитывать неопределённость и изменчивость данных, характерных для климатических и экономических процессов. В качестве предметной области рассмотрены метеоданные в одном из регионов России.

Целью данной статьи является разработка подходов к обработке больших массивов данных для СППР с использованием методов нечёткой логики и машинного обучения.

• 1    Нечёткая логика и нечёткие множества

Применение принципов нечёткой логики стало ключевым фактором в повышении устойчивости моделей прогнозирования.

Например, в работе [1] предложен многоступенчатый метод оперативного прогнозирования скорости ветра, который сочетает ансамблевый подход на основе модели прогнозирования погоды, нечёткую систему для извлечения данных и оптимизацию. Модель учитывает различные горизонтальные разрешения и исходные поля, что позволяет улучшить точность прогнозирования. В [2] представлен комбинированный интервал прогнозирования на основе нечёткой логики для прогнозирования ветровой энергии.

Применение методов машинного обучения и нечёткой логики позволяет повысить точность прогнозирования. Например, в [3] использована модель прогнозирования и улучшенный алгоритм кластеризации для установления функции нечёткого разделения. В [4] предложена модель прогнозирования концентраций загрязняющих веществ на основе исторических данных о погоде и загрязнении. Используются нечёткие модели для обработки неточных и неопределённых данных, что позволяет прогнозировать уровни загрязнения. В [5] предложен метод прогнозирования временных рядов на основе интуиционистских нечётких множеств, учитывающий неопределённость в данных. Метод показал высокую эффективность по сравнению с другими подходами на основе интуиционистских нечётких множеств. В [6] предложены классификация многокритериальных методов принятия решений и правила их выбора при разработке специализированного программного обеспечения для СППР. В [7] предложен подход к оценке технического состояния электрооборудования, основанный на использовании взвешенных нечётких правил. Данный подход позволяет учитывать нечёткий характер исходных данных. В [8] приведён анализ, моделирование и прогноз урожайности сельскохозяйственных культур с учётом динамики изменения природно-климатических характеристик путём применения методики нечёткой логики. Модель прогнозирования урожайности на основе нечёткой логики учитывает динамику климатических изменений. В [9] предложена методика оценки рисков снижения полевой всхожести зерновых культур, учитывающая степень кондиционности семенного материала на основе моделей нечёткой логики.

Системы прогнозирования на основе нечётких временных рядов представляют собой надёжный инструмент для работы с неопределённостью в данных временных рядов. Развитию теоретических основ и практического применения нечётких систем прогнозирования в различных областях посвящены работы [10-14].

Гранулирование временного ряда представляет собой процесс группировки данных временного ряда в более крупные временные интервалы, который позволяет: упростить структуры данных за счёт снижения их объёма; уменьшить влияния «шума» и случайных колебаний; повысить скорость обработки данных; улучшить визуализацию и интерпретацию временных рядов (см. таблицу 1).

Таблица 1 – Операции в гранулировании данных

Операция	Краткое описание
Классификация [15]	Назначение временным рядам одного из заранее определённых классов.
Кластеризация [16]	Группировка данных на основе их схожести.
Сегментация [17]	Разбиение временного ряда на значимые сегменты, расположенные последовательно.
Резюмирование [18]	Создание компактного представления данных, сохраняющего ключевые характеристики.
Ассоциативные правила [19]	Поиск правил, относящихся к временным рядам.
Оптимизация [20]	Поиск оптимальных параметров для сжатия данных.

Представленные в таблице 1 операции гранулирования данных могут включать элементы нечёткой логики. Нечёткая логика используется в следующих задачах:

группировка данных с возможностью одному объекту принадлежать одновременно нескольким или всем кластерам, но с различной степенью принадлежности ( нечёткая кластеризация ) [21];

разбиение временного ряда на сегменты с учётом нечётких границ между ними ( нечёткая сегментация ) [22];

вывод на базе нечёткой онтологии, который используется для резюмирования состояния сложной технической системы ( нечёткое резюмирование ) [23] и др.

В исследовании климатических факторов, которые часто изменяются в зависимости от временных сезонов, применён метод гранулирования с использованием нечёткого резюмирования временного ряда [24, 25].

Нечёткая логика позволяет работать с неточными или неопределёнными данными, оперируя степенями принадлежности к множеству в диапазоне от 0 до 1.

Пусть Х - некоторое универсальное множество. Для нечёткого множества A степень принадлежности каждого элемента x е X этому множеству является действительным числом ^А(x), принадлежащим отрезку [0,1]. Функция ^А(x)=0, если x £ A; цА(x)=1, если x е A ; 0<^А(x)<1, если x принадлежит множеству А частично.

Функция, описывающая, как элементы универсального множества X относятся к нечёткому множеству A , называется функцией принадлежности . В настоящем исследовании использована треугольная функция принадлежности, представленная в виде:

и , ( x ) = max 0,min

x - a c - x У

\

b - a’c - b J)

, a <  b <  c.

Нечёткая логика позволяет оперировать лингвистическими переменными, значения которых задаются словами естественного языка. В разрабатываемой базе знаний для каждого временного сезона созданы лингвистические переменные: холодная , умеренная и тёплая . Логический вывод (дефаззификация) выполняется с использованием метода центра тяжести:

* y ^*

E x i- ^ а ( x i )

i

E ^а (xi-)

i                          , где У - лингвистическая переменная для соответствующего сезона; цА(xi) - функция принадлежности нечёткого множества А; xiE X - нечёткие значения, принадлежащие конечному универсальному множеству.

• 2    Представление и обработка данных

  Исходные данные для исследования включали климатические данные: средние ежедневные значения температуры воздуха и количества осадков в Республике Татарстан в период с января 1881 года по октябрь 2024 года¹. Формат записи используемых данных

имеет вид:

Station идентификатор метеорологической станции Всемирной метеорологической организации;

Year      год, в который были обработаны данные;

Month    месяц, в котором были собраны данные, представленный в числовом формате (01-12);

Day      день месяца, в который были собраны данные, в числовом формате (01-31);

TMEAN среднесуточная температура воздуха, измеряемая в градусах Цельсия;

R         суточная сумма осадков, измеряемая в миллиметрах.

Климатические данные организованы в виде таблицы, где каждая строка соответствует определённому временному интервалу (например, день, месяц), а столбцы содержат показатели, такие как температура воздуха, количество осадков и др. В ходе обработки данных выполнены: проверка на наличие пропущенных значений, выбросов и «шумов»; нормализация и очистка данных для обеспечения их качества и пригодности для дальнейшего анализа. Для использования нечёткой логики введён дополнительный категориальный признак, отражающий сезонную принадлежность каждой даты (зима, весна, лето, осень). Учёт сезонности позволяет применить метод гранулирования для сжатия набора данных, что способствует снижению его размерности.

• 3    Гранулирование нечётких временных рядов

  

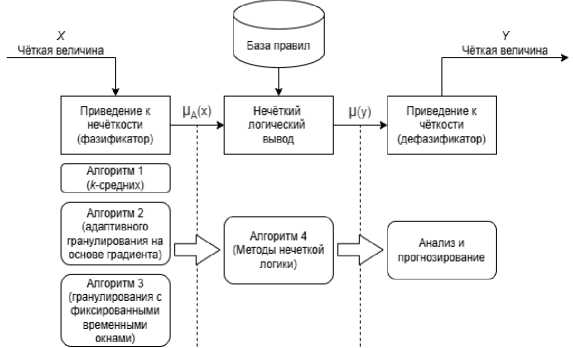
  Рисунок 1 - Этапы анализа данных

  
  

Гранулирование выполнено с помощью нечёткой логики. Основные этапы анализа данных включают: фаззификацию (приведение к нечёткости) чёткой величины ( x ); базу правил (базу знаний); дефаззификацию (приведение к чёткости) нечёткой величины для получения точного значения (у ) (см. рисунок 1).

Алгоритм 1 (k-средних) применён на предварительном этапе исследования для автоматического определения границ гранул, рассматривающихся в качестве кластеров для группировки схожих участков ряда. На рисунке 2 представлена схема работы алгоритма к-средних (2а) и

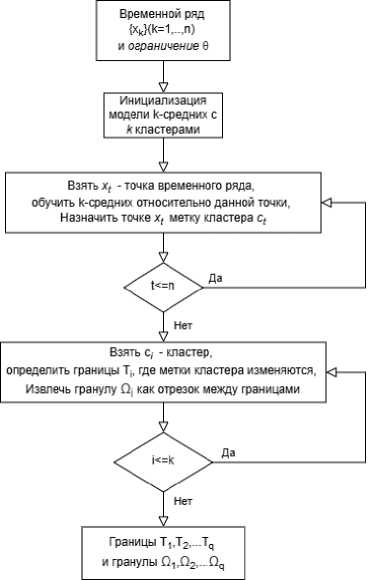
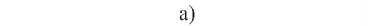
результаты кластеризации температурного временного ряда (2б). Алгоритм зависит от значения к (количество кластеров), которое необходимо указывать для выполнения кластеризации. Средняя сложность алгоритма оценивается как O ( k*n*t ) где к - заданное количество кластеров, n - количество выборок, t -

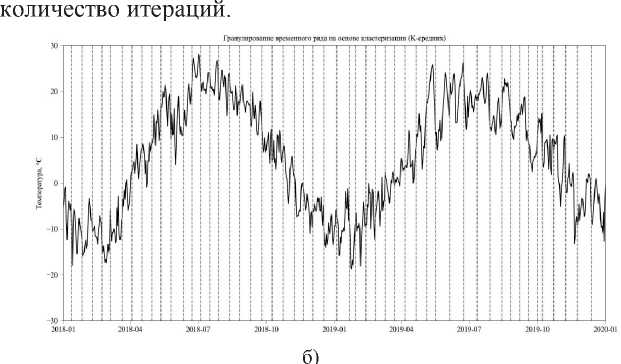
Рисунок 2 - Схема алгоритма (а) и результат гранулирования на основе кластеризации с использованием алгоритма к -средних (б) (временной ряд температур c 01.01.2018 по 01.01.2020, границы гранул выделены прерывистыми вертикальными линиями)

При разных значениях k изменяется скорость работы алгоритма, но может происходить и его остановка в точках локальных минимумов. В этом случае все оставшиеся значения будут отнесены к этому кластеру. Кластеры обозначаются c i , общее количество кластеров - q, длина временного ряда - n, T i - индекс исходного временного ряда, с которого начинается гранула i .

В качестве старта алгоритма берётся временной ряд { xk }( k =1,..., n ) и определяются: границы гранул (V i = 1, ..,q,Ti = [T^Tf], где: Т^ (индекс левой границы) - начальная точка гранулы, Т( (индекс правой границы) - конечная точка гранулы (условия: 7[ <7^ ^ 7^, Т ^f £ {1,,и}); гранулы: Л t = {х_к | = = 7^,..., 7^ ).

Алгоритм 2. Алгоритм адаптив-

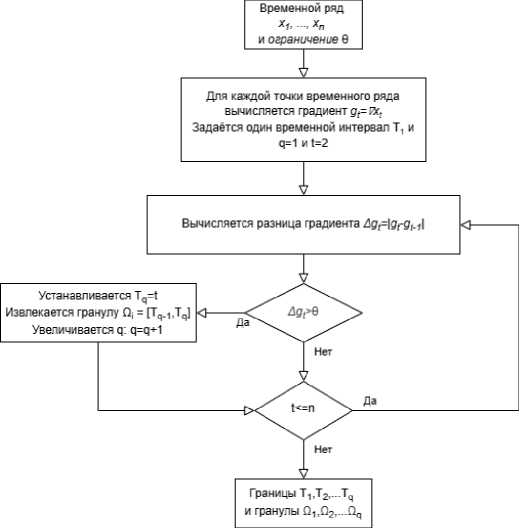
Рисунок 3 - Алгоритм адаптивного гранулирования на основе градиента

ного гранулирования на основе градиента (см. рисунок 3).

В ходе работы алгоритма доопределяются переменные, отвечающие за вычисление градиента по временным промежуткам - gt. За основной критерий берётся разница данных градиентов Дgt, которая оценивается относительно заранее установленного ограничения 0. Параметром, отвечающим за накопление количества временных интервалов, соответствующих количеству гранул является переменная q. Для прохода по всем временным интервалам используется переменная t, отражающая начальное количество временных интервалов. Алгоритма отличается простотой реализации и низкими вычислительными затратами на этапе инициализации. Недостатками являются самостоятельное определение порогового значения для производной, что может повлиять на результат гранулирования, а также сложность вычислений. Результат обработки данных этим алгоритмом представлен на рисунке 4.

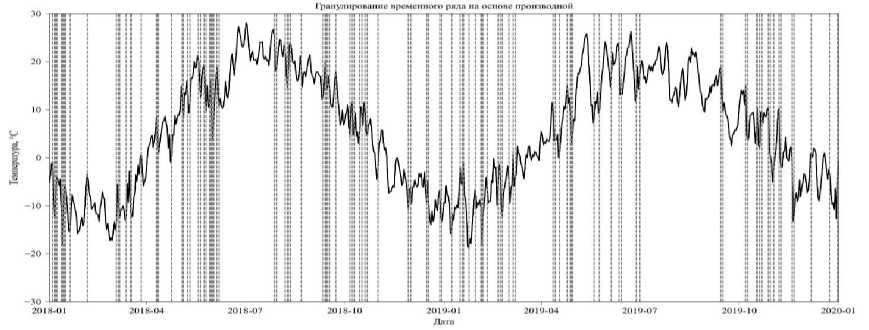
Рисунок 4 - Гранулирование временного ряда на основе градиента (границы гранул выделены прерывистыми вертикальными линиями)

Алгоритм 3. Алгоритм гранулирования с фиксированными

(рисунок 5). Он отражает выделение подпоследовательностей исходного возрастающего временного ряда в виде отдельных кластеров, содержащих основную информацию. Подобно первому алгоритму берутся границы T i . Итерации для временного ряда происходят по ∈ , границы сдвигаются на

∈ для сохранения порядка следования. Метод устойчив и может работать на временных рядах большого объёма. Результаты представлены на рисунке 6.

временными окнами

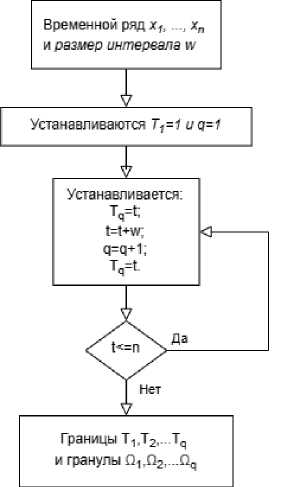
Рисунок 5 – Алгоритм гранулирования с фиксированными временными окнами

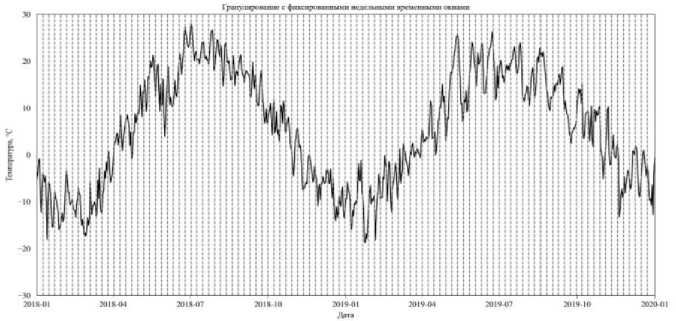
Рисунок 6 – Гранулирование с фиксированными недельными временными окнами

Алгоритмы 1-3 позволяют преобразовать временной ряд ежедневных температур в последовательность гранул, представляющих собой массив среднесуточных температур в течение одной недели (Ω ). Граница определяет индекс исходного временного ряда, с которого начинается гранула i . Затем каждая гранула проходит процесс фаззификации для дальнейшего её использования в формировании правил.

Алгоритм 4. Алгоритм фаззификации гранул с использованием методов нечёткой логики . Алгоритм (рисунок 7) позволяет привести чёткие численные значения к нечётким гранулам, выраженным на естественном языке [26]. Были созданы 12 лингвистических переменных, отражающих сезонные статистики S для каждого временного сезона, например, для сезона зима созданы лингвистические переменные: « холодная» , « умеренная» и « тёплая» .

В исследовании реализован гибридный алгоритм фаззификации сочетающий треугольные функции принадлежности для температурных данных (программная библиотека scikit-fuzzy 2 ) и гауссовы функции для сезонных параметров. Алгоритм обработки температурных временных рядов включает следующие этапы:

• 1)    ввод и предобработка данных: На вход подаётся гранула - массив из семи температурных значений (недельный временной ряд); Данные нормализуются в диапазон температур, соответствующий лингвистическим переменным.

• 2)    фаззификация: для температурных значений вычисляются степени принадлежности к 12 нечётким множествам: три температурных терма («холодная», «умеренная», «тёплая») с треугольными функциями принадлежности и четыре сезонных терма «зима», «весна», «лето», «осень» (с использованием гауссовых функций принадлежности);

• 3)    агрегирование: для каждого из 12 множеств вычисляется средняя степень принадлежности по всем семи точкам гранулы;

• 4)    логический вывод (дефаззификация): формируется итоговый вектор признаков гранулы. Вектор используется для активации правил из таблицы 2.

Fuzzy logic toolkit for SciPy. DOI 10.5281/zenodo.802396. –

Результатом работы Алгоритма 4 является вектор F = [Д ,Д >--->Д 2 ], где каждый элемент Д представляет собой среднюю степень принадлежности гранулы к соответствующему лингвистическому терму (например, Д - «холодная зима», Д -«умеренная зима», Д - «тёплая зима», Д - «холодная весна» и т.д. по порядку сезонов и температурных термов). Этот вектор F является формализованным признаковым описанием гранулы, количественно отражающим её неопределённость и недельную изменчивость. Он непосредственно используется для активации продукционных правил из таблицы 2 в процессе нечёткого вывода.

Предложенный подход к гранулированию, основанный на методах нечёткой логики (Алгоритм 4), обеспечил сжатие данных - объём выборки сократился с 52 534 до 7 504 точек (коэффициент сжатия ≈85%). Это реализовано путём вычисления для каждой недельной гранулы вектора F из 12 признаков. Таким образом, вектор F формализует нечёткие характеристики исходного недельного интервала, включая неопределённость (значения признаков в [0,1]) и изменчивость (различное распределение признаков у разных гранул).

• 4 Пример моделирования биоклиматического потенциала

Для проверки работоспособности предложенных подходов разработан прототип СППР для моделирования биоклиматического потенциала (БКП) экспертами предметной области. Фрагмент анализа БКП представлен на рисунке 8. В таблице 2 представлен фрагмент структуры базы знаний, которая включает набор продукционных правил, условий логического вывода и адаптивные интервалы для функций принадлежности, которые можно изменять в зависимости от региона и климата.

Функции принадлежности для сезонных параметров заданы в виде гауссовских кривых, определяемых параметрами среднего значения (среднее) и стандартного отклонения (о). Поскольку данные функции асимптотически стремятся к нулю, дополнительно вводятся ограниченные интервалы, в пределах которых рассматривается их ненулевая часть.

Сезоны представлены в виде числовых значений: «Зима» - 0, «Весна» - 1, «Лето» - 2, «Осень» - 3 и формализованы через полуинтервал [0, 4), где: [0,1) соответствует зиме, [1,2) - весне, [2,3) - лету, [3,4) - осени. Такое представление обеспечивает математическую корректность работы непрерывных функций принадлежности при переходе между

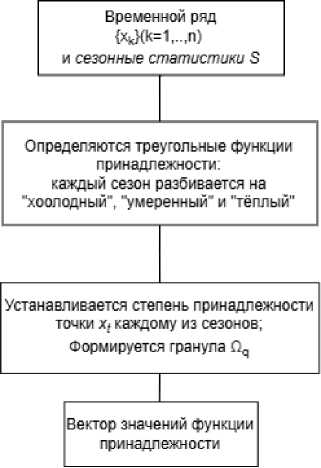
Рисунок 7 - Алгоритм гранулирования на основе нечёткого представления

сезонами, исключая неоднозначности на границах годового цикла.

В реализованном прототипе СППР применён алгоритм нечёткого вывода на основе заданных параметров модели (сезон и температура) в соответствии с Алгоритмом 4 (фаззифи-кация ^ агрегирование ^ дефаззификация) и последующим логическим выводом на основе продукционных правил.

Пример правила R 4 (в таблице 2)

Условие: температура: [5, 25] (гауссова функция, среднее = 10, о = 5) — «умеренная»); сезон: [2.5, 3.5]

(гауссова функция среднее = 3, о = 0.5) - «осень»).

Вывод: «БКП средний».

Логика: Умеренная температура в осенний сезон чаще даёт «средний БКП».

Таблица 2 - Фрагмент базы правил моделирования биоклиматического потенциала (БКП)

Правило	Условие	Вывод	Интервалы и функции принадлежности
1	Если температура холодная И сезон зима	БКП низкий	Температура: [-10, 10] (гауссова функция, среднее = -5, о = 5) Сезон: [0, 1] (гауссова функция, среднее = 0, о = 0.5)
2	Если температура умеренная И сезон весна	БКП средний	Температура: [5, 25] (гауссова функция, среднее = 10, о = 5) Сезон: [0.5, 1.5] (гауссова функция, среднее = 1, о = 0.5)
3	Если температура тёплая И сезон лето	БКП высокий	Температура: [20, 40] (гауссова функция, среднее = 25, о = 5) Сезон: [1.5, 2.5] (гауссова функция, среднее = 2, о = 0.5)
4	Если температура умеренная И сезон осень	БКП средний	Температура: [5, 25] (гауссова функция, среднее = 10, о = 5) Сезон: [2.5, 3.5] (гауссова функция, среднее = 3, о = 0.5)
5	Если температура холодная И сезон осень	БКП низкий	Температура: [-10, 10] (гауссова функция, среднее = -5, о = 5) Сезон: [2.5, 3.5] (гауссова функция, среднее = 3, о = 0.5)

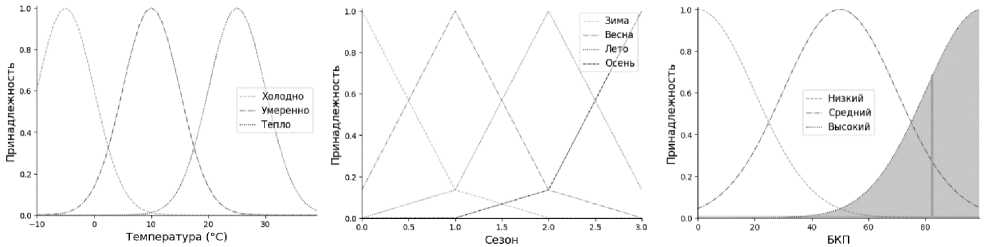
Рисунок 8 - Фрагмент анализа биоклиматического потенциала

Процесс нечёткого вывода БКП (на основе вектора признаков F) включает следующие шаги:

• 1)    Активация правил: каждое продукционное правило из таблицы 2 активируется путём выбора соответствующего элемента (или комбинации элементов) из вектора , который представляет среднюю степень принадлежности гранулы к лингвистическому терму условия правила.

• ■    Пример активации правила R4 (таблица 2): («Если Температура умеренная И Сезон осень ^ БКП средний») условие соответствует лингвистическому терму «умеренная осень». В векторе признаков F этот терм представлен отдельным элементом (Д _г в предположенном порядке термов). Значение этого элемента (средняя степень принадлежности гранулы к терму «умеренная осень») непосредственно определяет степень истинности условия правила R ₄.

• ■    Степень истинности антецедента (условия) правила рассчитывается как значение выбранного элемента вектора F (для правил с одним простым условием). Для правил с оператором «И» между несколькими элементами (см. реализацию ниже) степень истинности вычислялась бы как агрегация (например, min или произведение) соответствующих элементов F.

• 2)    Активизация заключений: полученная для каждого правила степень истинности используется для «обрезки» (или масштабирования) функции принадлежности выходного терма БКП, указанного в заключении этого правила.

• 3)    Агрегирование выходов: активизированные выходные термы БКП (результаты всех сработавших правил) объединяются в одно нечёткое множество с помощью операции максимума ( max ).

• 4)    Дефаззификация: к итоговому агрегированному нечёткому множеству выходной переменной (БКП) применяется метод центра тяжести для получения чёткого числового значения или категории биоклиматического потенциала.

Реализация правил вывода БКП с использованием вектора F (scikit-fuzzy):

В прототипе СППР с использованием библиотеки scikit-fuzzy продукционные правила активируются путём проверки значений конкретных элементов вектора F относительно за- данных порогов активации ᵢ. Упрощённый вид реализованных правил соответствует линг вистическим правилам таблицы 2:

R i : Если F "холодная зима"] > 9 1 ТО БКП низкий; // Условие: Холодная Зима

R ₂: Если F "умеренная весна"] > 9₂ ТО БКП средний; // Условие: Умеренная Весна

R ₃: Если F ["тёплая лето"] > 9₃ ТО БКП высокий; // Условие: Тёплое Лето

R ₄: Если F "умеренная осень"] > 9 4 ТО БКП средний; // Условие: Умеренная Осень

R ₅: Если F "холодная осень"] > 9 5 ТО БКП низкий; // Условие: Холодная Осень, где 0 i - пороговые значения, определяющие минимальную степень принадлежности для активации соответствующего правила (в коде 9 1 -9 5 ).

Пример активации правил.

Пусть предполагаемый порядок термов имеет вид в первой грануле с вектором: F = f еature s[0] = [0.087,0.534,0.377,0.510,0.489,0.0,0.0,0.0,0.0,0.584,0.415,0.0], где наибольшие значения имеют индексы 1, 3, 4, 9 и 10:

• ■    F "умеренная зима"] (индекс 1) = 0.534

• ■    F "холодная весна"] (индекс 3) = 0.510

• ■    F "умеренная весна"] (индекс 4) = 0.489

• ■    F "холодная осень"] (индекс 9) = 0.584

• ■    F "умеренная осень"] (индекс 10) = 0.415

При порогах, например, 0₁=0.5, 0₂=0.4, 0₄=0.4, 0₅ =0.5, активируются правила: R ₁ (Умеренная Зима: 0.534 > 0.5); R ₂ (Умеренная Весна: 0.489 > 0.4); R( (Умеренная Осень: 0.415 > 0.4); R ₅ (Холодная Осень: 0.584 > 0.5).

Итоговый вывод БКП будет определяться степенями истинности активированных правил ( R 1 , R 2 , R 4 , R 5 ) и методом дефаззификации (центра тяжести).

Предлагаемая структура продукционных правил обладает модульной архитектурой , позволяющей адаптировать параметры моделирования к различным климатическим условиям. Адаптация осуществляется путём:

• ■    корректировки функций принадлежности: изменение гауссовских (сезон) и треугольных (температура) функций на этапе фаззификации (Алгоритм 4); модификация границ термов БКП;

• ■    динамической настройки базы правил: добавление/изменение/удаление продукционных правил; изменение весовых коэффициентов; настройка порогов активации 0 i для элементов вектора F;

• ■    регулировки диапазонов входных переменных .

Заключение

В работе предложен подход к обработке данных метеорологических временных рядов, основанный на методах нечёткой логики. Ключевыми результатами исследования являются: ■ Алгоритм нечёткого гранулирования . Алгоритм 4 - гибридный алгоритм, использующий треугольные функции принадлежности для температурных данных и гауссовы функции для сезонных параметров. Алгоритм преобразует исходные чёткие данные в нечёткие гранулы, представленные 12-мерными векторами признаков F. Эти векторы количественно отражают характерную неопределённость и недельную изменчивость исходных температурных колебаний.

• ■    Сжатие данных . Применение алгоритма гранулирования позволило сократить объём исходных данных с 52 534 до 7 504 точек (коэффициент сжатия ≈85%) при сохранении ключевых статистических характеристик и семантического содержания данных, воплощённого в векторах F.

• ■    СППР для моделирования БКП . СППР использует формализованные гранулы (векторы ) для активации набора адаптивных продукционных правил нечёткого вывода, реализующих экспертные знания о взаимосвязи температуры, сезона и БКП. Модульная

архитектура СППР может позволить настраивать функции принадлежности, пороги активации правил и саму базу правил под различные климатические условия.